7.1: Introducción

El diseño de un circuito receptor o transmisor requiere el diseño de una cascada de módulos que logre un rango dinámico óptimo al tiempo que administra el consumo de energía de CC. Como ejemplo, la etapa de conversión de frecuencia de un receptor se muestra en la Figura\(\PageIndex{1}\). Los filtros de microcinta y las líneas de transmisión se fabrican sobre sustratos de alúmina. Los troqueles semiconductores y los capacitores de desacoplamiento del chip, así como los módulos de alúmina, se epoxidan a una estera que fue serigrafiada en una carcasa de latón. La estera proporciona un alivio de tensión (permitiendo diferencias en los coeficientes térmicos de expansión) y una interfaz conductora entre los sustratos de alúmina y semiconductores y la carcasa de latón. Los módulos y las matrices están interconectados por cables de unión dispuestos como dos o más cables de unión en paralelo para reducir la inductancia. Los cables de unión se unen a las almohadillas en los condensadores de desacoplamiento. Estos módulos, a excepción de los filtros, se describen en este capítulo.

El capítulo comienza con la investigación de una cascada de módulos dadas las características de distorsión de los módulos individuales. Junto con un tratamiento más temprano del ruido de un sistema en cascada, esto define el rango dinámico. Un sistema de microondas que comprende una cascada de módulos principalmente de dos puertos y debe diseñarse para minimizar simultáneamente el ruido, la distorsión, el consumo de energía de CC, las emisiones espurias y maximizar el rango dinámico. Hay necesariamente una compensación de estos parámetros de rendimiento y esta compensación está en el corazón del diseño del sistema. Lo que hace que esto sea particularmente desafiante es que las redes de dos puertos se diseñan por separado y allí

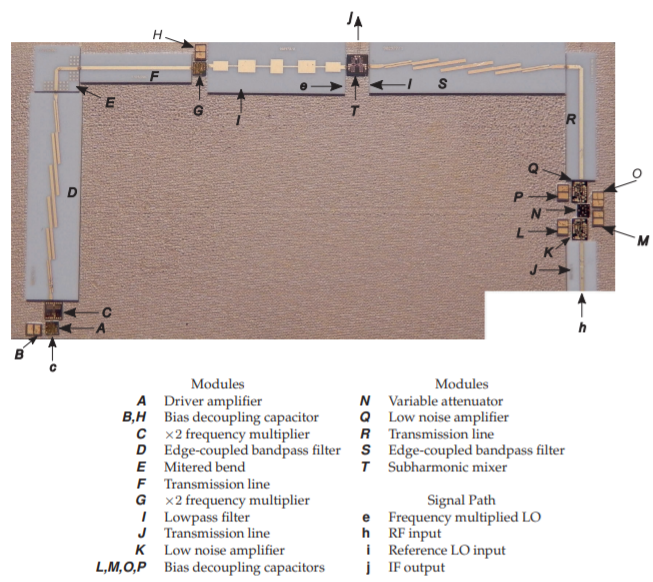
Figura\(\PageIndex{1}\): La porción de conversión de frecuencia del\(15\text{ GHz}\) receptor que se muestra en la Figura 7.6.1. La entrada de RF at\(\mathbf{h}\) se centra en\(15\text{ GHz}\) y se amplifica y filtra antes de ser presentada a un mezclador subarmónico en\(\mathbf{T}\). El LO de referencia at\(\mathbf{c}\) es sintonizable de\(1601\) a\(1742\text{ MHz}\) y se multiplica en frecuencia dos veces\(\mathbf{G}\), at\(\mathbf{C}\) y, y luego se presenta como LO al mezclador armónico en at\(\mathbf{T}\). El LO va desde\(6403\) hasta\(6968\text{ MHz}\). La salida IF en\(\mathbf{j}\) rangos de\(465\) a\(1595\text{ MHz}\).

es una caracterización incompleta del desempeño. De hecho, la única manera precisa de determinar el rendimiento general del sistema sería tener los esquemas a nivel de circuito de cada módulo y luego realizar una simulación de nivel de circuito en el dominio del tiempo del sistema completo usando las señales moduladas reales. Incluso si todos los detalles estuvieran disponibles, el tiempo de simulación sería prohibitivo y es poco probable que una simulación en el dominio del tiempo tenga la fidelidad necesaria. Esto es cierto incluso si una gran parte de un sistema se implementa en el mismo chip. Por lo tanto, el diseño del sistema debe usar un proceso metódico utilizando parámetros incompletos a nivel de módulo, como la compresión de\(1\text{ dB}\) ganancia, la cifra de ruido y las caracterizaciones de intercepción de tercer orden. El diseño del sistema suele ser conservador para el peor de los casos. A veces esto es demasiado conservador y hay que hacer concesiones.

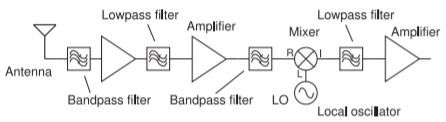
Figura\(\PageIndex{2}\): Receptor como cascada de módulos.

Las pruebas y el ajuste de prototipos fabricados son esenciales.

En esta sección se describen dos enfoques para el diseño de módulos en cascada; el método presupuestal y el método de contribución. En el método de presupuesto las métricas de ganancia y rendimiento de ruido se asignan inicialmente a cada etapa en cascada y luego estas se ajustan en un simulador de sistema para iterar hacia una solución óptima. En el método de contribución el enfoque está en el rango dinámico y a cada módulo crítico se le asigna el mismo rango dinámico y a partir de esto se realiza una asignación inicial de cifra de ruido, ganancia y linealidad requerida para cada módulo. La optimización del desempeño del sistema procede como con el método presupuestal. Generalmente esta optimización se debe realizar manualmente utilizando la experiencia ya que a menudo es difícil cuantificar lo que es un óptimo. También algunas decisiones de diseño requieren la adquisición de módulos de mayor costo y si un módulo es de bajo costo, entonces tiene sentido asignar un alto rango dinámico a dicho módulo para reducir los requisitos en otros módulos de mayor costo. Quizás un módulo deba ser rediseñado o diseñado internamente en lugar de ser de origen externo. Estas no son decisiones simples. Al final, el sistema con módulos en cascada debe ser competitivo en costos y rendimiento, y reducir el tiempo de comercialización es una ventaja competitiva.