2.7: Ejercicios
- Page ID
- 86226
- Encuentra la densidad\(\mathrm{f}_{S_{n}}(t)\) Erlang convolucionando\(\mathrm{f}_{X}(x)=\lambda \exp (-\lambda x)\) consigo mismo\(n\) tiempos.
- Encuentra la función generadora de momento de\(X\) (o encuentra la transformación de Laplace de\(f_{X}(x)\)), y usa esta para encontrar la función generadora de momento (o transformar Laplace) de\(S_{n}=X_{1}+X_{2}+\dots+X_n\). Invierta su resultado para encontrar\(\mathrm{f}_{S_{n}}(t)\).
- Encuentra la densidad Erlang comenzando con\ ref {2.15} y luego calculando la densidad marginal para\(S_{n}\).
- Contestar
- Encuentra la media, varianza y función generadora de momento de\(N(t)\), según lo dado por (2.16).
- Demostrar por convolución discreta que la suma de dos autov's independientes de Poisson es de nuevo Poisson.
- Demostrar usando las propiedades del proceso de Poisson que la suma de dos rv independientes de Poisson debe ser Poisson.
- Contestar
El propósito de este ejercicio es dar una derivación alterna de la distribución de Poisson para\(N(t)\), el número de llegadas en un proceso de Poisson hasta el momento\(t\). \(\lambda\)Sea la tasa del proceso.
- Encuentra la probabilidad condicional\(\operatorname{Pr}\left\{N(t)=n \mid S_{n}=\tau\right\}\) para todos\(\tau \leq t\).
- Usando la densidad Erlang para\(S_{n}\), use\ ref {a} para encontrar\(\operatorname{Pr}\{N(t)=n\}\).
- Contestar
Supongamos que un proceso de conteo\(\{N(t) ; t>0\}\) tiene las propiedades de incremento independientes y estacionarias y satisface\ ref {2.16} (para todos\(t>0\)). \(X_{1}\)Sea la época de la primera llegada y\(X_{n}\) sea el tiempo de interllegada entre la\(n-1^{\mathrm{st}}\) y la\(n\) th llegada. Utilice únicamente estos supuestos para hacer las siguientes partes de este ejercicio.
- \(\operatorname{Pr}\left\{X_{1}>x\right\}=e^{-\lambda x}\)Demuéstralo.
- \(S_{n-1}\)Sea la época de la\(n-1^{\mathrm{st}}\) llegada. \(\operatorname{Pr}\left\{X_{n}>x \mid S_{n-1}=\tau\right\}=e^{-\lambda x}\)Demuéstralo.
- Para cada uno\(n>1\), mostrar eso\(\operatorname{Pr}\left\{X_{n}>x\right\}=e^{-\lambda x}\) y que\(X_{n}\) es independiente de\(S_{n-1}\).
- Argumentan que\(X_{n}\) es independiente de\(X_{1}, X_{2}, \ldots X_{n-1}\).
- Contestar
El objetivo de este ejercicio es mostrar que la secuencia de PMF's para un proceso de conteo de Bernoulli no especifica el proceso. Es decir, saber que\(N(t)\) satisface la distribución binomial para todos\(t\) no significa que el proceso sea Bernoulli. Esto nos ayuda a entender por qué la segunda definición de un proceso de Poisson requiere incrementos estacionarios e independientes, así como la distribución de Poisson para\(N(t)\).
- Dejar\(Y_{1}, Y_{2}, Y_{3}, \ldots\) ser una secuencia de rv binarios en la que cada rv es 0 o 1 con igual probabilidad. Encontrar una distribución conjunta para\(Y_{1}, Y_{2}, Y_{3}\) que satisfaga la distribución binomial,\(\mathbf{p}_{N(t)}(k)=\left(\begin{array}{l} t \\ k \end{array}\right) 2^{-k}\) para\(t=1,2,3\) y\(0 \leq k \leq t\), pero para la cual no\(Y_{1}, Y_{2}, Y_{3}\) son independientes.
Una solución simple para esto contiene cuatro 3-tuplas con probabilidad 1/8 cada una, dos 3-tuplas con probabilidad 1/4 cada una, y dos 3-tuplas con probabilidad 0. Tenga en cuenta que al hacer las llegadas subsiguientes IID y equiprobables, se tiene un ejemplo donde\(N(t)\) es binomial para todos t pero el proceso no es Bernoulli. Pista: Usa el binomio for\(t=3\) para encontrar dos 3-tuplas que deben tener probabilidad 1/8. Combine esto con el binomio\(t=2\) para encontrar otras dos 3-tuplas que deben tener probabilidad 1/8. Finalmente, observe las restricciones impuestas por la distribución binomial sobre las cuatro 3-tuplas restantes.
- Generalizar la parte a) al caso donde\(Y_{1}, Y_{2}, Y_{3}\) satisfacer\(\operatorname{Pr}\left\{Y_{i}=1\right\}=p\) y\(\operatorname{Pr}\left\{Y_{i}=0\right\}=1-p\). Asumir\(p<1 / 2\) y encontrar una distribución conjunta sobre\(Y_{1}, Y_{2}, Y_{3}\) que satisfaga la distribución binomial, pero para la cual la 3-tupla (0, 1, 1) tiene probabilidad cero.
- Más generalmente, ver un PMF conjunto en\(t\) tuplas binarias como un vector no negativo en un espacio vectorial\(2^{t}\) dimensional. Cada probabilidad binomial\(\mathbf{p}_{N(\tau)}(k)=\left(\begin{array}{l} \tau \\ k \end{array}\right) p^{k}(1-p)^{\tau-k}\) constituye una restricción lineal sobre este vector. Para cada uno\(\tau\), mostrar que una de estas restricciones puede ser reemplazada por la restricción que los componentes del vector sumen a 1.
- Usando la parte c), muestran que en la mayoría\((t+1) t / 2+1\) de las restricciones binomiales son linealmente independientes. Tenga en cuenta que esto significa que el espacio lineal de vectores que satisfacen estas restricciones binomiales tiene al menos dimensión\(2^{t}-(t+1) t / 2-1\). Este espacio lineal tiene dimensión 1 para\(t=3\), explicando los resultados en las partes a) y b). Tiene una dimensión cada vez mayor para\(t>3\), lo que sugiere que las restricciones binomiales son relativamente ineficaz para restringir el PMF conjunto de una distribución conjunta. Se requiere más trabajo para el caso de\(t>3\) por todas las restricciones de desigualdad, pero resulta que esta gran dimensionalidad permanece.
- Contestar
Dejar\(h(x)\) ser una función positiva de una variable real que satisface\(h(x+t)=h(x)+h(t)\) y deja\(h(1)=c\).
- Muéstralo para entero\(k>0, h(k)=k c\).
- Muéstralo para entero\(j>0, h(1 / j)=c / j\).
- Mostrar eso para todos los enteros\(k, j, h(k / j)=c k / j\).
- Las partes anteriores muestran que\(h(x)\) es lineal en números racionales positivos. Para matemáticos muy quisquillosos, esto no garantiza que\(h(x)\) sea lineal en números reales positivos. Mostrar que si también\(h(x)\) es monotónico en\(x\), entonces\(h(x)\) es lineal en\(x>0\).
- Contestar
Supongamos que un proceso de conteo\(\{N(t) ; t>0\}\) tiene las propiedades de incremento independientes y estacionarias y, para todos\(t>0\), satisface
\ (\ begin {alineado}
&\ nombreoperador {Pr}\ {\ tilde {N} (t, t+\ delta) =0\} ^\} =1-\ lambda\ delta+o (\ delta)\\\
&\ nombreoperador {Pr}\ {\ tilde ancho {N} (t, t+\ delta) =1\} ^\} =\ lambda\ delta+o (\ delta)\\
&\ nombreoperador {Pr}\ {\ Widetilde {N} (t, t+\ delta) >1\} ^\} =o (\ delta)
\ end {alineado}\)
- Dejemos\(\mathrm{F}_{0}(\tau)=\operatorname{Pr}\{N(\tau)=0\}\) y demuestre eso\(d \mathrm{~F}_{0}(\tau) / d \tau=-\lambda \mathrm{F}_{0}(\tau)\).
- Demostrar que\(X_{1}\), el tiempo de la primera llegada, es exponencial con parámetro\(\lambda\).
- Dejemos\(\mathrm{F}_{n}(\tau)=\operatorname{Pr}\left\{\tilde{N}(t, t+\tau)=0 \mid S_{n-1}=t\right\}^\}\) y demuestre eso\(d \mathrm{~F}_{n}(\tau) / d \tau=-\lambda \mathrm{F}_{n}(\tau)\).
- Argumentan que\(X_{n}\) es exponencial con parámetro\(\lambda\) e independiente de tiempos de llegada más tempranos.
- Contestar
Dejar\(t>0\) ser un tiempo arbitrario, dejar\(Z_{1}\) ser la duración del intervalo desde\(t\) hasta la siguiente llegada después\(t\). Que\(Z_{m}\), para cada uno\(m>1\), sea el tiempo de interllegada desde la época de la\(m-1^{\mathrm{st}}\) llegada posterior\(t\) hasta la\(m\) th llegada.
- Dado eso\(N(t)=n\), explicar por qué\(Z_{m}=X_{m+n}\) para\(m>1\) y\(Z_{1}=X_{n+1}-t+S_{n}\).
- Condicional en\(N(t)=n\) y\(S_{n}=\tau\), muestra que\(Z_{1}, Z_{2}, \ldots\) son IID.
- Demostrar que\(Z_{1}, Z_{2}, \ldots\) son IID.
- Contestar
Consideremos una aproximación de “Bernoulli que se encoge”\(N_{\delta}(m \delta)=Y_{1}+\cdots+Y_{m}\) a un proceso de Poisson como se describe en la subsección 2.2.5.
- Demostrar que
\ (\ nombreoperador {Pr}\ izquierda\ {N_ {\ delta} (m\ delta) =n\ derecha\} =\ izquierda (\ begin {array} {c} m\\ n
\ end {array}\ derecha) (\ lambda\ delta) ^ {n} (1-\ lambda\ delta) ^ {m-n}\) - Dejar\(t=m \delta\), y dejar que\(t\) se fije para el resto del ejercicio. Explicar por qué
\ (\ lim _ {\ delta\ fila derecha 0}\ nombreoperador {Pr}\ izquierda\ {N_ {\ delta} (t) =n\ derecha\} =\ lim _ {m\ fila derecha\ infty}\ izquierda (\ begin {array} {c} m\ n
\ end {array}\ derecha)\ izquierda (\ frac {\ lambda t} {m}\ derecha) ^ {n}\ izquierda (1-\ frac {\ lambda t} {m}\ derecha) ^ {m-n}\)donde se toma el límite de la izquierda sobre los valores de\(\delta\) esa división\(t\).
- Derivar las siguientes dos igualdades:
\ (\ lim _ {m\ fila derecha\ infty}\ izquierda (\ begin {array} {l} m\\ n
\ end {array}\ derecha)\ frac {\} {1}} {m^ {n}} =\ frac {1} {n!} ;\ quad\ texto {y}\ quad\ lim _ {m\ fila derecha\ infty}\ izquierda (1-\ frac {\ lambda t} {m}\ derecha) ^ {m-n} =e^ {-\ lambda t}\) - Concluimos de esto que para todos\(t\) y cada uno\(n\),\(\lim _{\delta \rightarrow 0} \operatorname{Pr}\left\{N_{\delta}(t)=n\right\}=\operatorname{Pr}\{N(t)=n\}\) donde\(\{N(t) ; t>0\}\) está un proceso de tasa de Poisson\(\lambda\).
- Contestar
Deja\(\{N(t) ; t>0\}\) ser un proceso de Poisson de tasa\(\lambda\).
- Encuentra la función de masa de probabilidad conjunta (PMF) de\(N(t), N(t+s)\) for\(s>0\).
- Encuentra\(\mathrm{E}[N(t) \cdot N(t+s)]\) para\(s>0\).
- Encuentra\(\mathrm{E}\left[\tilde{N}\left(t_{1}, t_{3}\right) \cdot \tilde{N}\left(t_{2}, t_{4}\right)\right]^\}\) dónde\(\tilde{N}(t, \tau)\) está el número de llegadas en\((t, \tau]\) y\(t_{1}<t_2<t_3<t_4\).
- Contestar
Un experimento elemental se realiza independientemente en\(N\) tiempos donde\(N\) se encuentra un rv de Poisson de media\(\lambda\). Dejar\(\left\{a_{1}, a_{2}, \ldots, a_{K}\right\}\) ser el conjunto de puntos de muestreo del experimento elemental y let\(\mathrm{p}_{k}, 1 \leq k \leq K\), denotar la probabilidad de\(a_{k}\).
- Let\(N_{k}\) denotar el número de experimentos elementales realizados para los que es la salida\(a_{k}\). Encuentra el PMF para\(N_{k}(1 \leq k \leq K)\). (Pista: no es necesario realizar ningún cálculo.)
- Encuentra el PMF para\(N_{1}+N_{2}\).
- Encuentra el PMF condicional para\(N_{1}\) dado eso\(N=n\).
- Encuentra el PMF condicional para\(N_{1}+N_{2}\) dado eso\(N=n\).
- Encuentra el PMF condicional para\(N\) dado eso\(N_{1}=n_{1}\).
- Contestar
A partir del tiempo 0, los autobuses en dirección norte llegan a 77 Mass. Avenida según un proceso de Poisson de tasa\(\lambda\). Los pasajeros llegan de acuerdo con un proceso de tarifa independiente de Poisson\(\mu\). Cuando llega un autobús, todos los clientes que esperan ingresan instantáneamente al autobús y los clientes posteriores esperan el siguiente autobús.
- Encuentra el PMF para el número de clientes que ingresan a un autobús (más específicamente, para cualquier dado\(m\), encuentra el PMF para el número de clientes que ingresan al bus\(m\) th).
- Encuentre el PMF para el número de clientes que ingresan al mésimo autobús dado que el intervalo entre llegadas entre autobús\(m-1\) y autobús\(m\) es\(x\).
- Dado que un autobús llega a la hora 10:30 PM, encuentra el PMF para el número de clientes que ingresan al siguiente autobús.
- Dado que un autobús llega a las 10:30 PM y ningún autobús llega entre las 10:30 y las 11, encuentra el PMF para el número de clientes en el siguiente autobús.
- Encuentre el PMF para la cantidad de clientes que esperan en algún momento dado, digamos a las 2:30 PM (supongamos que los procesos comenzaron infinitamente lejos en el pasado). Pista: piensa en lo que sucede moviéndose hacia atrás en el tiempo a partir de las 2:30 PM.
- Encuentra el PMF para el número de clientes que se suben al siguiente autobús para llegar después de las 2:30. (Pista: esto es diferente de la parte a); mira cuidadosamente la parte e).
- Dado que llego a esperar un autobús a las 2:30 PM, encuentre el PMF para el número de clientes que suban al siguiente autobús.
- Contestar
- Demostrar que las épocas de llegada de un proceso de Poisson satisfacen
\(\mathrm{f}_{\boldsymbol{S}^{(n)} \mid S_{n+1}}\left(\boldsymbol{s}^{(n)} \mid s_{n+1}\right)=n ! / s_{n+1}^{n}\)
Pista: Esto es fácil si usas solo los resultados de la Sección 2.2.2.
- Contraste esto con el resultado del Teorema 2.5.1
- Contestar
Ecuación\ ref {2.41} da\(\mathbf{f}_{S_{i}}\left(s_{i} \mid N(t)=n\right)\), que es la densidad de la variable aleatoria\(S_{i}\) condicional\(N(t)=n\) para\(n \geq i\). Multiplica esta expresión por\(\operatorname{Pr}\{N(t)=n\}\) y suma\(n\) para encontrar\(\mathrm{f}_{S_{i}}\left(s_{i}\right)\); verifica que tu respuesta sea efectivamente la densidad Erlang.
- Contestar
Considera generalizar el proceso de llegada masiva en la Figura 2.5. Supongamos que las épocas en las que ocurren las llegadas forman un proceso\(\{N(t) ; t>0\}\) de tasa de Poisson\(\lambda\). En cada época de llegada,\(S_{n}\), el número de llegadas\(Z_{n}\),, satisface\(\left.\operatorname{Pr}\left\{Z_{n}=1\right\}=p, \operatorname{Pr}\left\{Z_{n}=2\right)\right\}=1-p\). Las variables\(Z_{n}\) son IID.
- \(\left\{N_{1}(t) ; t>0\right\}\)Sea el proceso de conteo de las épocas en las que ocurren las llegadas individuales. Encuentra el PMF de\(N_{1}(t)\) como una función de\(t\). De igual manera, deja\(\left\{N_{2}(t) ; t \geq 0\right\}\) ser el proceso de conteo de las épocas en las que se producen las dobles llegadas. Encuentra el PMF de\(N_{2}(t)\) como una función de t.
- \(\left\{N_{B}(t) ; t \geq 0\right\}\)Sea el proceso de conteo del número total de llegadas. Dar una expresión para el PMF de\(N_{B}(t)\) como una función de\(t\)
- Contestar
- Para un proceso de conteo de Poisson de tasa\(\lambda\), encuentre la densidad de probabilidad conjunta de\(S_{1}, S_{2}, \ldots, S_{n-1}\) condicional on\(S_{n}=t\).
- Encuentra\(\operatorname{Pr}\left\{X_{1}>\tau \mid S_{n}=t\right\}\).
- Encuentra\(\operatorname{Pr}\left\{X_{i}>\tau \mid S_{n}=t\right\}\) para\(1 \leq i \leq n\).
- Encuentra la densidad\(f_{S_{i} \mid S_{n}}\left(s_{i} \mid t\right)\) para\(1 \leq i \leq n-1\).
- Dar una explicación de la sorprendente similitud entre la condición\(N(t)=n-1\) y la condición\(S_{n}=t\).
- Contestar
- Para un proceso de Poisson de tasa\(\lambda\), encontrar\(\operatorname{Pr}\left\{N(t)=n \mid S_{1}=\tau\right\}\) para\(t>\tau\) y\(n \geq 1\).
- Usando esto, encuentra\(\mathrm{f}_{S_{1}}(\tau \mid N(t)=n)\)
- Verifica tu respuesta contra (2.40).
- Contestar
Considera un proceso de conteo en el que la tasa es una rv\(\Lambda\) con densidad de probabilidad\(\mathrm{f}_{\Lambda}(\lambda)=\alpha e^{-\alpha \lambda}\) para\(\lambda>0\). Condicional a un valor de muestra dado\(\lambda\) para la tasa, el proceso de conteo es un proceso de Poisson de tasa\(\lambda\) (es decir, la naturaleza primero elige un valor de muestra\(\lambda\) y luego genera una ruta de muestreo de un proceso de Poisson de esa tasa\(\lambda\)).
- ¿Qué es\(\operatorname{Pr}\{N(t)=n \mid \Lambda=\lambda\}\), dónde\(N(t)\) se da el número de llegadas en el intervalo\((0, t]\) para algunos\(t>0\)?
- Demostrar que\(\operatorname{Pr}\{N(t)=n\}\), el PMF incondicional para\(N(t)\), viene dado por
\(\operatorname{Pr}\{N(t)=n\}=\frac{\alpha t^{n}}{(t+\alpha)^{n+1}}\)
- Encontrar\(\mathrm{f}_{\Lambda}(\lambda \mid N(t)=n)\), la densidad de\(\lambda\) condicional en\(N(t)=n\).
- Encuentra\(\mathrm{E}[\Lambda \mid N(t)=n]\) e interpreta tu resultado para muy pequeños\(t\) con\(n=0\) y para muy grandes\(t\) con\(n\) grandes.
- Encuentra\(\mathrm{E}\left[\Lambda \mid N(t)=n, S_{1}, S_{2}, \ldots, S_{n}\right]\). (Pista: considerar la distribución de\(S_{1}, \ldots, S_{n}\) condicional\(N(t)\) y\(\Lambda\)). Encuentra\(\mathrm{E}[\Lambda \mid N(t)=n, N(\tau)=m]\) para algunos\(\tau<t\).
- Contestar
- Usa la Ecuación\ ref {2.41} para encontrar\(\mathrm{E}\left[S_{i} \mid N(t)=n\right]\). Sugerencia: Al integrar\(s_{i} \mathrm{f}_{S_{i}}\left(s_{i} \mid N(t)=n\right)\), compare esta integral con\(\mathrm{f}_{S_{i+1}}\left(s_{i} \mid N(t)=n+1\right)\) y use el hecho de que esta última expresión es una densidad de probabilidad.
- Encuentra el segundo momento y la varianza de\(S_{i}\) condicional on\(N(t)=n\). Pista: Extiende la pista anterior.
- Supongamos que\(n\) es extraño, y considera\(i=(n+1) / 2\). Cuál es la relación entre\(S_{i}\), condicional y la mediana muestral de n variables aleatorias uniformes IID.\(N(t)=n\)
- Dar una ley débil de grandes números para la mediana anterior.
- Contestar
Supongamos que los autos entran en una autopista unidireccional de longitud infinita, carril infinito a una tasa de\(\lambda\) Poisson El auto\(i\) th para entrar elige una velocidad\(V_{i}\) y viaja a esta velocidad. Supongamos que los rv\(V_{i}{ }^{\prime} \mathrm{s}\) son positivos independientes que tienen una distribución común F. Derivar la distribución del número de autos que se localizan en un intervalo (0,\(a\)) en el momento\(t\).
- Contestar
Considera una\(\mathrm{M} / \mathrm{G} / \infty\) cola, es decir, una cola con llegadas de Poisson de tarifa\(\lambda\) en la que cada llegada\(i\), independiente de otras llegadas, permanece en el sistema por un tiempo\(X_{i}\), donde\(\left\{X_{i} ; i \geq 1\right\}\) hay un conjunto de IID rv con alguna función de distribución dada\(\mathrm{F}(x)\).
Se puede suponer que el número de llegadas en cualquier intervalo\((t, t+\epsilon)\) que aún se encuentren en el sistema en algún momento posterior\(\tau \geq t+\epsilon\) es estadísticamente independiente del número de llegadas en\((t, t+\epsilon)\) ese mismo intervalo que hayan salido del sistema por tiempo\(\tau\).
- Dejar\(N(\tau)\) ser el número de clientes en el sistema en el momento\(\tau\). Encuentra la media,\(m(\tau)\), de\(N(\tau)\) y encuentra\(\operatorname{Pr}\{N(\tau)=n\}\).
- \(D(\tau)\)Sea el número de clientes que han salido del sistema por tiempo\(\tau\). Encuentra la media,\(\mathrm{E}[D(\tau)]\), y encuentra\(\operatorname{Pr}\{D(\tau)=d\}\).
- Encuentra\(\operatorname{Pr}\{N(\tau)=n, D(\tau)=d\}\)
- Dejar\(A(\tau)\) ser el número total de llegadas hasta el momento\(\tau\). Encuentra\(\operatorname{Pr}\{N(\tau)=n \mid A(\tau)=a\}\).
- Encuentra\(\operatorname{Pr}\{D(\tau+\epsilon)-D(\tau)=d\}\)
- Contestar
Los votantes de un pueblo determinado llegan al lugar de votación de acuerdo con un proceso de Poisson de\(\lambda=100\) electores tarifarios por hora. Los votantes votan independientemente por candidato\(A\) y candidato\(B\) cada uno con probabilidad 1/2. Supongamos que la votación inicia en el tiempo 0 y continúa indefinidamente.
- Condicional a que 1000 electores lleguen durante las primeras 10 horas de votación, encuentre la probabilidad de que el candidato\(A\) reciba\(n\) de esos votos.
- De nuevo condicional a 1000 electores durante las primeras 10 horas, encuentra la probabilidad de que el candidato\(A\) reciba\(n\) votos en las primeras 4 horas de votación.
- \(T\)Sea la época de la llegada del primer votante votante votando por candidato\(A\). Encuentra la densidad de\(T\).
- Encuentra el PMF del número de electores para candidato\(B\) que llegan antes que el primer elector para\(A\).
- Definir al votante\(n\) th como una inversión si el elector\(n\) th vota por un candidato diferente al\(n-1^{s t}\). Por ejemplo, en la secuencia de votos\(AABAABB\), los electores tercero, cuarto y sexto son reversiones; el tercero y sexto son\(A\) a\(B\) reversiones y el cuarto es\(B\) a\(A\) reversión. Dejar\(N(t)\) ser el número de reversiones hasta el tiempo\(t\) (\(t\)en horas). ¿Es el proceso de\(\{N(t) ; t>0\}\) Poisson? Explique.
- Encuentra el tiempo esperado (en horas) entre reversiones.
- Encuentra la densidad de probabilidad del tiempo entre reversiones.
- Encuentra la densidad del tiempo de uno\(A\) a la\(B\) reversión al siguiente\(A\) a la\(B\) reversión.
- Contestar
Dejar\(\left\{N_{1}(t) ; t>0\right\}\) ser un proceso de conteo de Poisson de tasa\(\lambda\). Supongamos que las llegadas de este proceso son encendidas y apagadas por llegadas de un segundo proceso independiente de Poisson\(\left\{N_{2}(t) ; t>0\right\}\) de tarifa\(\gamma\).
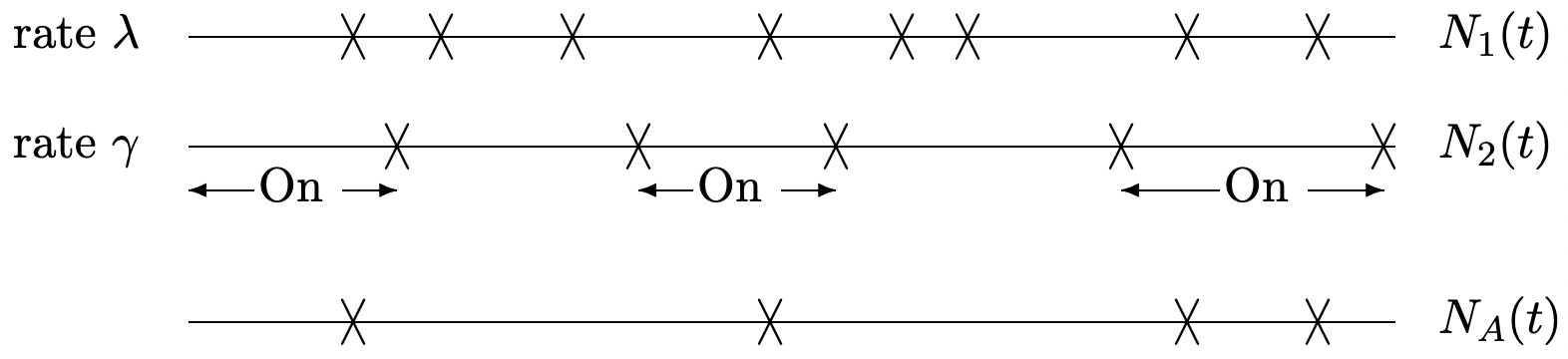
Dejar\(\left\{N_{A}(t) ; t \geq 0\right\}\) ser el proceso de conmutación; es decir,\(N_{A}(t)\) incluye las llegadas de\(\{N_{1}(t) ; t> 0\}\) durante periodos cuando\(N_{2}(t)\) es par y excluye las llegadas de\(\left\{N_{1}(t) ; t>0\right\}\) mientras\(N_{2}(t)\) es impar.
- Encuentra el PMF para el número de llegadas del primer proceso,\(\left\{N_{1}(t) ; t>0\right\}\), durante el\(n\) th periodo en el que el interruptor está encendido.
- Dado que la primera llegada para el segundo proceso ocurre en época\(\tau\), encuentra el PMF condicional para el número de llegadas del primer proceso hasta\(\tau\).
- Dado que el número de llegadas del primer proceso, hasta la primera llegada para el segundo proceso, es\(n\), encontrar la densidad para la época de la primera llegada del segundo proceso.
- Encuentra la densidad del tiempo entre llegadas para\(\left\{N_{A}(t) ; t \geq 0\right\}\). Nota: Esta parte es bastante desordenada y se hace más fácilmente a través de las transformadas de Laplace.
- Contestar
Modelaremos el torneo de ajedrez entre Fisher y Spassky como un proceso estocástico. Dejar\(X_{i}\), para\(i \geq 1\), ser la duración del i-ésimo juego y asumir que\(\left\{X_{i} ; i \geq 1\right\}\) es un conjunto de IID distribuidos exponencialmente rv cada uno con densidad\(\mathrm{f}_{X}(x)=\lambda e^{-\lambda x}\). Supongamos que cada juego (independientemente de todos los demás juegos, e independientemente de la duración de los juegos) es ganado por Fisher con probabilidad\(p\), por Spassky con probabilidad\(q\), y es un empate con probabilidad\(1-p-q\). El primer jugador en ganar n juegos se define como el ganador, pero consideramos que el partido hasta el punto de ganar está incrustado en una secuencia interminable de juegos.
- Encuentra la distribución del tiempo, desde el inicio del partido, hasta la finalización del primer juego que se gana (es decir, que no es un empate). Caracterizar el proceso de la cantidad\(\{N(t) ; t>0\}\) de juegos ganados hasta e incluyendo el tiempo\(t\). Caracterizar el proceso de la cantidad\(\left\{N_{F}(t) ; t \geq 0\right\}\) de juegos ganados por Fisher y el número\(\left\{N_{S}(t) ; t \geq 0\right\}\) ganado por Spassky.
- Para lo que resta del problema, supongamos que la probabilidad de un empate es cero; es decir, eso\(p+q=1\). ¿Cuántos de los primeros\(2 n-1\) juegos debe ser ganado por Fisher para poder ganar el partido?
- ¿Cuál es la probabilidad de que Fisher gane el partido? Tu respuesta no debe involucrar ninguna integral. Pista: considera la secuencia interminable de juegos y usa la parte b).
- \(T\)Sea la época en la que se completa el partido (es decir, gana Fisher o Spassky). Encuentra la función de distribución de\(T\).
- Encuentra la probabilidad de que Fisher gane y que\(T\) se encuentre en el intervalo\((t, t+\delta)\) para arbitrariamente pequeños\(\delta\).
- Contestar
- Encuentra la densidad condicional de\(S_{i+1}\), condicional\(N(t)=n\) y\(S_{i}=s_{i}\).
- Utilice la parte a) para encontrar la densidad articular de\(S_{1}, \ldots, S_{n}\) condicional on\(N(t)=n\). Verifica que tu respuesta esté de acuerdo con (2.37).
- Contestar
Un proceso de Poisson bidimensional es un proceso de ocurrencia aleatoria de puntos especiales en el plano de tal manera que\ ref {i} para cualquier región del área\(A\) el número de puntos especiales en esa región tiene una distribución de Poisson con media\(\lambda A\), y (ii) el número de puntos especiales en regiones no superpuestas es independiente. Para tal proceso considerar una ubicación arbitraria en el plano y dejar\(X\) denotar su distancia desde su punto especial más cercano (donde la distancia se mide de la manera euclidiana habitual). Demostrar que
- \(\operatorname{Pr}\{X>t\}=\exp \left(-\lambda \pi t^{2}\right)\)
- \(\mathrm{E}[X]=1 /(2 \sqrt{\lambda})\)
- Contestar
Este problema pretende mostrar que se puede analizar el comportamiento a largo plazo de los problemas de cola usando solo nociones de medios y varianzas, pero que dicho análisis es incómodo, justificando comprender la fuerte ley de los grandes números. Considera una cola M/G/1. El proceso de llegada es Poisson con\(\lambda=1\). El tiempo de servicio esperado,\(\mathrm{E}[Y]\), es 1/2 y la varianza del tiempo de servicio se da para que sea 1.
- Considerar\(S_{n}\), la hora de la enésima llegada, para\(n=10^{12}\). Con alta probabilidad,\(S_{n}\) se ubicará dentro de 3 derivaciones estándar de su media. Encuentra y compara esta media y el\(3 \sigma\) rango.
- \(V_{n}\)Sea la cantidad total de tiempo durante el cual el servidor está ocupado con estas\(n\) llegadas (es decir, la suma de los tiempos de\(10^{12}\) servicio). Encuentra la media y el\(3 \sigma\) rango de\(V_{n}\).
- Encuentre la media y el\(3 \sigma\) rango de\(I_{n}\), la cantidad total de tiempo que el servidor está inactivo hasta\(S_{n}\) (tómese\(I_{n}\) como\(S_{n}-V_{n}\), ignorando así cualquier tiempo de servicio posterior\(S_{n}\)).
- Un periodo de inactividad comienza cuando el servidor completa un servicio y no hay llegadas en espera; termina en la siguiente llegada. Encuentra la media y varianza de un periodo de inactividad. ¿Los sucesivos periodos de inactividad son IID?
- Combine\ ref {c} y\ ref {d} para estimar el número total de periodos de inactividad hasta el tiempo\(S_{n}\). Utilice esto para estimar el número total de periodos ocupados.
- Combine\ ref {e} y\ ref {b} para estimar la duración esperada de un período ocupado.
- Contestar
El propósito de este problema es ilustrar que para un proceso de llegada con intervalos interllegados independientes pero no distribuidos idénticamente\(X_{1}, X_{2}, \ldots\), el número de llegadas\(N(t)\) en el intervalo\((0, t]\) puede ser una rv defectuosa. Es decir, el 'proceso de contado' no es un proceso estocástico según nuestras definiciones. Esto ilustra que es necesario probar que los rv de conteo para un proceso de renovación son en realidad rv.
- Deje que la función de distribución del\(i\) intervalo entre llegadas para un proceso de llegada sea\(\mathrm{F}_{X_{i}}\left(x_{i}\right)=1-\exp \left(-\alpha^{i} x_{i}\right)\) para algunos fijos\(\alpha \in(0,1)\). Deja\(S_{n}=X_{1}+\cdots X_{n}\) y demuestra que
\(\mathrm{E}\left[S_{n}\right]=\frac{1-\alpha^{n-1}}{1-\alpha}\)
- Esboce una ruta de muestra 'razonable' para\(N(t)\).
- Encuentra\(\sigma_{S_{n}}^{2}\)
- Usa la desigualdad de Chebyshev\(\operatorname{Pr}\left\{S_{n} \geq t\right\}\) para encontrar un límite superior en el\(\operatorname{Pr}\{N(t) \leq n\}\) que sea menor que 1 para todos\(n\) y para lo suficientemente grande\(t\). Usa esto para demostrar que\(N(t)\) es defectuoso por lo suficientemente grande\(t\).
- Contestar