4.3: Ley Fuerte para Procesos de Renovación

Para tener una idea intuitiva de por qué\(N(t) / t\) debería acercarse\(1 / \bar{X}\) para grandes\(t\), considere la Figura 4.2. Para cualquier función de muestra dada de\(\{N(t) ; t>0\}\), tenga en cuenta que, para cualquier dada\(t\),\(N(t) / t \) es la pendiente de una línea recta desde el origen hasta el punto\((t, N(t))\). A\(t\) medida que aumenta, esta pendiente disminuye en el intervalo entre cada par adyacente de épocas de llegada y luego salta hacia arriba en la siguiente época de llegada. Para expresar esto como una ecuación, tenga en cuenta que\(t\) se encuentra entre la llegada\(N(t)\) th (que ocurre en\(S_{N(t)}\)) y la\((N(t)+1)\) th llegada (que ocurre en\(S_{N(t)+1}\)). Así, para todos los puntos de muestreo,

\[\frac{N(t)}{S_{N(t)}} \geq \frac{N(t)}{t}>\frac{N(t)}{S_{N(t)+1}}.\label{4.7} \]

Figura 4.2: Comparación de una función muestral de\(N(t) / t\) con\(\frac{N(t)}{S_{N(t)}}\) y\(\frac{N(t)}{S_{N(t)+1}}\) para el mismo punto de muestreo. Tenga en cuenta que para el punto de muestra dado,\(N(t)\) es el número de llegadas hasta e incluyendo\(t\), y así\(S_{N(t)}\) es la época de la última llegada antes o en el momento\(t\). De igual manera,\(S_{N(t)+1}\) es la época de la primera llegada estrictamente después del tiempo\(t\).

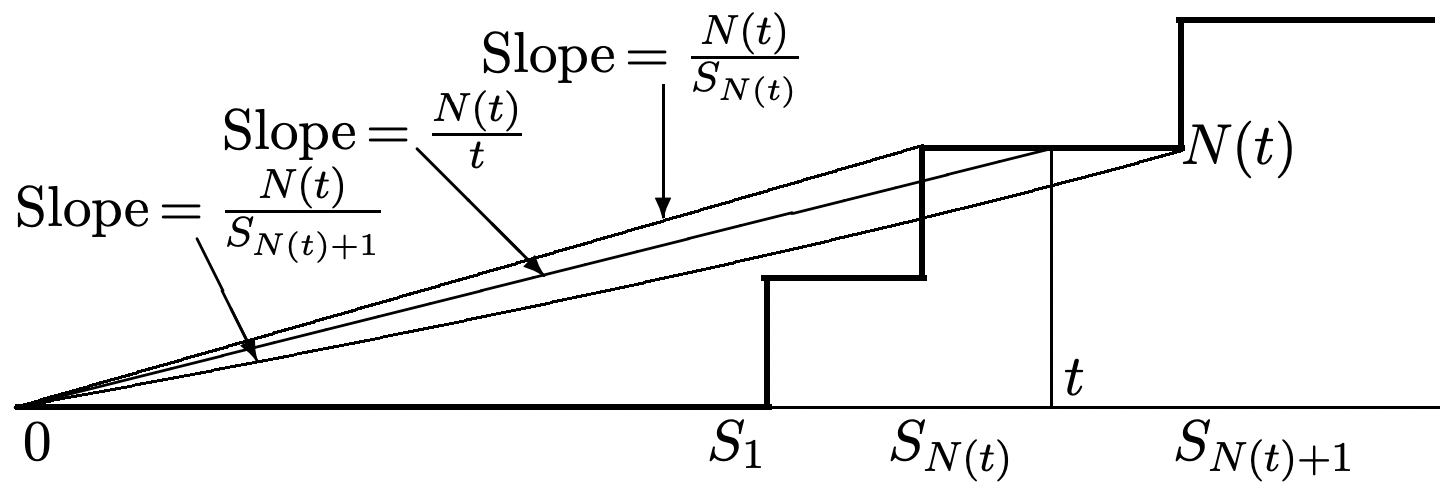
Queremos mostrar intuitivamente por qué la pendiente\(N(t) / t\) en la figura se acerca\(1 / \bar{X}\) como\(t \rightarrow\infty\). A medida que\(t\) aumenta, supondríamos que\(N(t)\) aumenta sin límite, es decir, que por cada llegada, otra llegada ocurre eventualmente. Suponiendo esto, el lado izquierdo de\ ref {4.7} aumenta con el aumento\(t\) como\(1 / S_{1}, 2 / S_{2}, \ldots, n / S_{n}, \ldots\), donde\(n=N(t)\). Dado que\(S_{n} / n\) converge a\(\bar{X}\) WP1 desde la fuerte ley de los grandes números, podríamos ser lo suficientemente valientes o perspicaces como para adivinar que\(n / S_{n}\) converge a\(1 / \bar{X}\).

Ahora estamos listos para declarar como teorema la ley fuerte para los procesos de renovación. Antes de probar el teorema, formulamos las dos conjeturas anteriores como lemmas y demostramos su validez.

Teorema 4.3.1 (Ley Fuerte para Procesos de Renovación).

Para un proceso de renovación con intervalo medio entre renovaciones\(\bar{X}<\infty\),\(\lim _{t \rightarrow \infty} N(t) / t=1 / \bar{X}\) WP1.

Lema 4.3.1

Dejar\(\{N(t) ; t>0\}\) ser un proceso de conteo de renovación con rv inter-renovaciones\(\left\{X_{n} ; n \geq 1\right\}\). Entonces (sea o no\(\bar{X}<\infty\)),\(\lim _{t \rightarrow \infty} N(t)=\infty\) WP1 y\(\lim _{t \rightarrow \infty} \mathrm{E}[N(t)]=\infty\).

Prueba

Tenga en cuenta que para cada punto de muestra\(\omega\),\(N(t, \omega)\) es una función de valor real no decreciente de\(t\) y por lo tanto tiene un límite finito o un límite infinito. Usando (4.1), la probabilidad de que este límite sea finito con un valor menor que cualquier dado\(n\) es

\(\lim _{t \rightarrow \infty} \operatorname{Pr}\{N(t)<n\}=\lim _{t \rightarrow \infty} \operatorname{Pr}\left\{S_{n}>t\right\}=1-\lim _{t \rightarrow \infty} \operatorname{Pr}\left\{S_{n} \leq t\right\}\).

Dado que los\(X_{i}\) son rv, las sumas también\(S_{n}\) son rv (es decir, no defectuosos) para cada uno\(n\) (ver Sección 1.3.7), y\(\lim _{t \rightarrow \infty} \operatorname{Pr}\left\{S_{n} \leq t\right\}=1\) por lo tanto para cada uno\(n\). Así\(\lim _{t \rightarrow \infty} \operatorname{Pr}\{N(t)<n\}=0\) para cada uno\(n\). Esto demuestra que el conjunto de puntos de muestreo\(\omega\) para los cuales\(\lim _{t \rightarrow \infty} N(t(\omega))<n\) tiene probabilidad 0 para todos\(n\). Así el conjunto de puntos de muestreo para los que\(\lim _{t \rightarrow \infty} N(t, \omega)\) es finito tiene probabilidad 0 y\(\lim _{t \rightarrow \infty} N(t)=\infty\) WP1.

A continuación,\(\mathrm{E}[N(t)]\) es no decreciente en\(t\), y por lo tanto tiene ya sea un límite finito o infinito como\(t \rightarrow \infty\). Para cada uno\(n\),\(\operatorname{Pr}\{N(t) \geq n\} \geq 1 / 2\) para lo suficientemente grande\(t\), y por lo tanto\(\mathrm{E}[N(t)] \geq n / 2\) para tal\(t\). Por lo tanto no\(\mathrm{E}[N(t)]\) puede tener límite finito como\(t \rightarrow \infty\), y\(\lim _{t \rightarrow \infty} \mathrm{E}[N(t)]=\infty\).

El siguiente lema es bastante más general que la segunda conjetura anterior, pero será útil en otros lugares. Esta es la formalización de la técnica utilizada al final de la prueba del SLLN.

Lema 4.3.2

Dejar\(\left\{Z_{n} ; n \geq 1\right\}\) ser una secuencia de rv tal que\(\lim _{n \rightarrow \infty} Z_{n}=\alpha\) WP1. Dejar\(f\) ser una función real valorada de una variable real que es continua en\(\alpha\). Entonces

\[\lim _{n \rightarrow \infty} f\left(Z_{n}\right)=f(\alpha) \quad \text{WP1}.\label{4.8} \]

Prueba

Primero vamos\(z_{1}, z_{2}, \ldots\), ser una secuencia de números reales tales que\(\lim _{n \rightarrow \infty} z_{n}=\alpha\). Continuidad de\(f\) al\(\alpha\) significa que para cada\(\epsilon>0\), hay\(\delta>0\) tal que\(|f(z)-f(\alpha)|<\epsilon\) para todos\(z\) tales que\(|z-\alpha|<\delta\). También, ya que\(\lim _{n \rightarrow \infty} z_{n}=\alpha\), sabemos que para cada\(\delta>0\), hay\(m\) tal que\(\left|z_{n}-\alpha\right| \leq \delta\) para todos\(n \geq m\). Armando estas dos declaraciones, sabemos que para cada\(\epsilon>0\), hay una m tal que\(\left|f\left(z_{n}\right)-f(\alpha)\right|<\epsilon\) para todos\(n \geq m\). Así\(\lim _{n \rightarrow \infty} f\left(z_{n}\right)=f(\alpha)\).

Si\(\omega\) hay algún punto de muestra tal que\(\lim _{n \rightarrow \infty} Z_{n}(\omega)=\alpha\), entonces\(\lim _{n \rightarrow \infty} f\left(Z_{n}(\omega)\right)=f(\alpha)\). Dado que este conjunto de puntos de muestra tiene probabilidad 1, sigue\ ref {4.8}.

Prueba de Teorema 4.3.1, Ley fuerte para procesos de renovación:

Ya que\(\operatorname{Pr}\{X>0\}=1\) para un proceso de renovación, vemos eso\(\bar{X}>0\). Escogiendo\(f(x)=1 / x\), vemos que\(f(x)\) es continuo en\(x=\bar{X}\). De Lema 4.3.2 se desprende que

\(\lim _{n \rightarrow \infty} \frac{n}{S_{n}}=\frac{1}{\bar{X}} \quad \text{WP1}.\)

A partir de Lema 4.3.1, sabemos que\(\lim _{t \rightarrow \infty} N(t)=\infty\) con probabilidad 1, entonces, con probabilidad 1,\(N(t)\) aumenta a través de todos los enteros no negativos a medida que\(t\) aumenta de 0 a\(\infty\). Así

\(\lim _{t \rightarrow \infty} \frac{N(t)}{S_{N(t)}}=\lim _{n \rightarrow \infty} \frac{n}{S_{n}}=\frac{1}{\bar{X}}\quad \text{WP1}.\)

Recordemos que\(N(t) / t\) está intercalado entre\(N(t) / S_{N(t)}\) y\(N(t) / S_{N(t)+1}\), para que podamos completar la prueba demostrando eso\(\lim _{t \rightarrow \infty} N(t) / S_{N(t)+1}=1 / \bar{X}\). Para mostrar esto,

\(\lim _{t \rightarrow \infty} \frac{N(t)}{S_{N(t)+1}}=\lim _{n \rightarrow \infty} \frac{n}{S_{n+1}}=\lim _{n \rightarrow \infty} \frac{n+1}{S_{n+1}} \frac{n}{n+1}=\frac{1}{\bar{X}} \quad \text{WP1}.\)

Hemos pasado por la prueba de este teorema con gran detalle, ya que algunas de las técnicas probablemente no son familiares para muchos lectores. Si uno vuelve a leer la prueba, después de familiarizarse con los detalles, la simplicidad del resultado será bastante llamativa. El teorema también es cierto si el intervalo medio entre renovaciones es infinito; esto puede verse mediante un argumento de truncamiento (ver Ejercicio 4.8).

Como se explica en la Sección 4.2.1, el Teorema 4.3.1 implica también la correspondiente ley débil de grandes números para\(N(t)\), es decir, para cualquiera\(\epsilon>0\),\(\lim _{t \rightarrow \infty} \operatorname{Pr}\{|N(t) / t-1 / \bar{X}| \geq \epsilon\}=0\)). Esta ley débil también podría derivarse de la débil ley de grandes números para\(S_{n}\) (Teorema 1.5.3). No lo perseguimos aquí, ya que la derivación es tediosa y poco instructiva. Como veremos, es la ley fuerte la que más útil es para los procesos de renovación.

La Figura 4.3 ayuda a dar un poco de apreciación de lo\(N(t)\) que dice y no dice la ley fuerte. La ley fuerte se ocupa de los promedios de tiempo\(\lim _{t \rightarrow \infty} N(t, \omega) / t\),, para puntos de muestra individuales\(\omega\); estos se indican en la figura como promedios horizontales, uno para cada uno\(\omega\). También es de interés mirar el tiempo y ensemble-promedios,\(\mathrm{E}[N(t) / t]\), mostrados en la figura como promedios verticales. Tenga en cuenta que\(N(t, \omega) / t\) es el promedio de tiempo número de renovaciones de 0 a\(t\), mientras que los\(\mathrm{E}[N(t) / t]\) promedios también sobre el conjunto. Por último, para enfocarse en las llegadas en las inmediaciones de un momento determinado\(t\), es de interés mirar el promedio del conjunto\(E[N(t+\delta)-N(t)] / \delta\).

Dada la fuerte ley para\(N(t)\), uno plantearía la hipótesis de que\(\mathrm{E}[N(t) / t]\) se acerca\(1 / \bar{X}\) como\(t \rightarrow \infty\). También se podría plantear la hipótesis de que\(\lim _{t \rightarrow \infty} \mathrm{E}[N(t+\delta)-N(t)] / \delta=1 / \bar{X}\), sujeto a algunas restricciones menores sobre\(\delta\). Estas hipótesis son correctas y se discuten en detalle en lo que sigue. Esta igualdad de medias de tiempo y medias de conjunto limitantes para procesos de renovación se traslada a un gran número de procesos estocásticos, y forma la base de la teoría ergódica. Estos resultados son importantes tanto para fines teóricos como prácticos. A veces es fácil encontrar promedios de tiempo (al igual que fue fácil encontrar el promedio de tiempo a\(N(t, \omega) / t\) partir de la fuerte ley de grandes números), y a veces es fácil encontrar promedios limitantes del conjunto. Poder equiparar los dos nos permite entonces alternar a voluntad entre tiempo y ensemble-promedios.

Figura 4.3: El promedio de tiempo en un punto de muestra\(\omega\), el promedio de tiempo y conjunto de 0 a un dado\(\tau\), y el promedio de conjunto en un intervalo\((t, t+\delta]\).

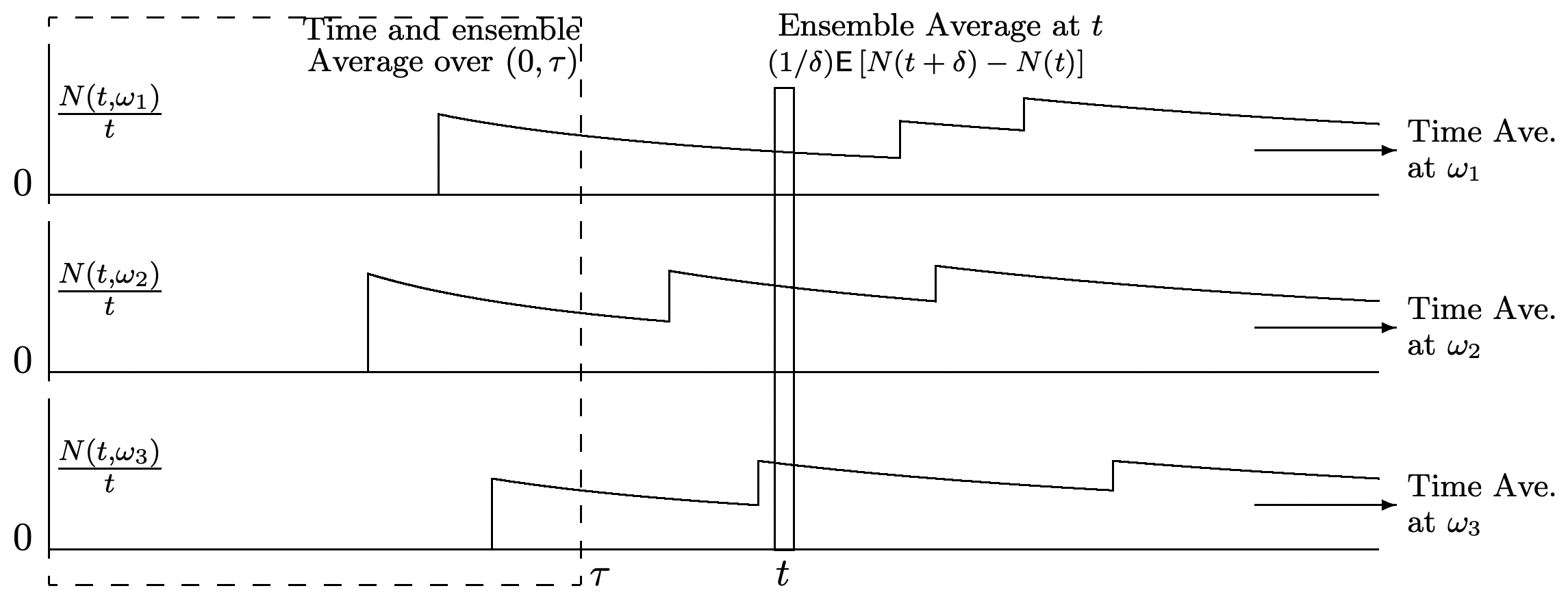
Tenga en cuenta que para igualar los promedios de tiempo y los promedios limitantes del conjunto, se requieren bastantes condiciones. Primero, el promedio de tiempo debe existir en el límite\(t \rightarrow \infty\) con probabilidad uno y también tener un valor fijo con probabilidad uno; segundo, el conjunto-promedio debe acercarse a un límite como\(t \rightarrow \infty\); y tercero, los límites deben ser los mismos. El siguiente ejemplo, para un proceso estocástico muy diferente a un proceso de renovación, muestra que la igualdad entre el tiempo y los promedios conjuntos no siempre se satisface para procesos arbitrarios.

Ejemplo 4.3.1

Dejar\(\left\{X_{i} ; i \geq 1\right\}\) ser una secuencia de variables aleatorias IID binarias, cada una tomando el valor 0 con probabilidad 1/2 y 2 con probabilidad 1/2. Dejar\(\left\{M_{n} ; n \geq 1\right\}\) ser el proceso del producto en el que\(M_{n}=X_{1} X_{2} \cdots X_{n}\). Ya que\(M_{n}=2^{n}\) si\(X_{1}\) a\(X_{n}\) cada uno se toma el valor 2 (un evento de probabilidad\(2^{-n}\)) y de\(M_{n}=0\) otra manera, vemos que\(\lim _{n \rightarrow \infty} M_{n}=0\) con probabilidad 1. También\(\mathrm{E}\left[M_{n}\right]=1\) para todos\(n \geq 1\). Así el promedio de tiempo existe y es igual a 0 con probabilidad 1 y el ensemble-promedio existe y es igual a 1 para todos\(n\), pero los dos son diferentes. El problema es que a medida que\(n\) aumenta, el evento atípico en el que\(M_{n}=2^{n}\) tiene una probabilidad que se aproxima a 0, pero aún tiene un efecto significativo en el conjunto-promedio.

Se aplaza más discusión sobre los promedios conjuntos a la Sección 4.6. Antes de eso, exponemos brevemente y discutimos el teorema del límite central para contar los procesos de renovación y luego introducir la noción de recompensas asociadas a los procesos de renovación.

Teorema 4.3.2 (Teorema de Límite Central (CLT) para\(N(t)\)).

Supongamos que los intervalos entre renovaciones para un proceso de conteo de renovación\(\{N(t) ; t>0\}\) tienen una desviación estándar finita\(\sigma>0\). Entonces

\[\lim _{t \rightarrow \infty} \operatorname{Pr}\left\{\frac{N(t)-t / \bar{X}}{\sigma \bar{X}^{-3 / 2} \sqrt{t}}<\alpha\right\}=\Phi(\alpha).\label{4.9} \]

donde\(\Phi(y)=\int_{-\infty}^{y} \frac{1}{\sqrt{2 \pi}} \exp \left(-x^{2} / 2\right) d x\).

Esto dice que la función de distribución\(N(t)\) tiende a la distribución gaussiana con media\(t / \bar{X}\) y desviación estándar\(\sigma \bar{X}^{-3 / 2} \sqrt{t}\).

Figura 4.4: Ilustración del teorema del límite central (CLT) para procesos de renovación. Un entero dado\(n\) se muestra en el eje vertical, y la media correspondiente,\(\mathrm{E}\left[S_{n}\right]=n \bar{X}\) se muestra en el eje horizontal. La línea horizontal con flechas a la altura\(n\) indica desviaciones\(\alpha\) estándar de\(\mathrm{E}\left[S_{n}\right]\), y la línea vertical con flechas indica la distancia a continuación\((t / \bar{X})\).

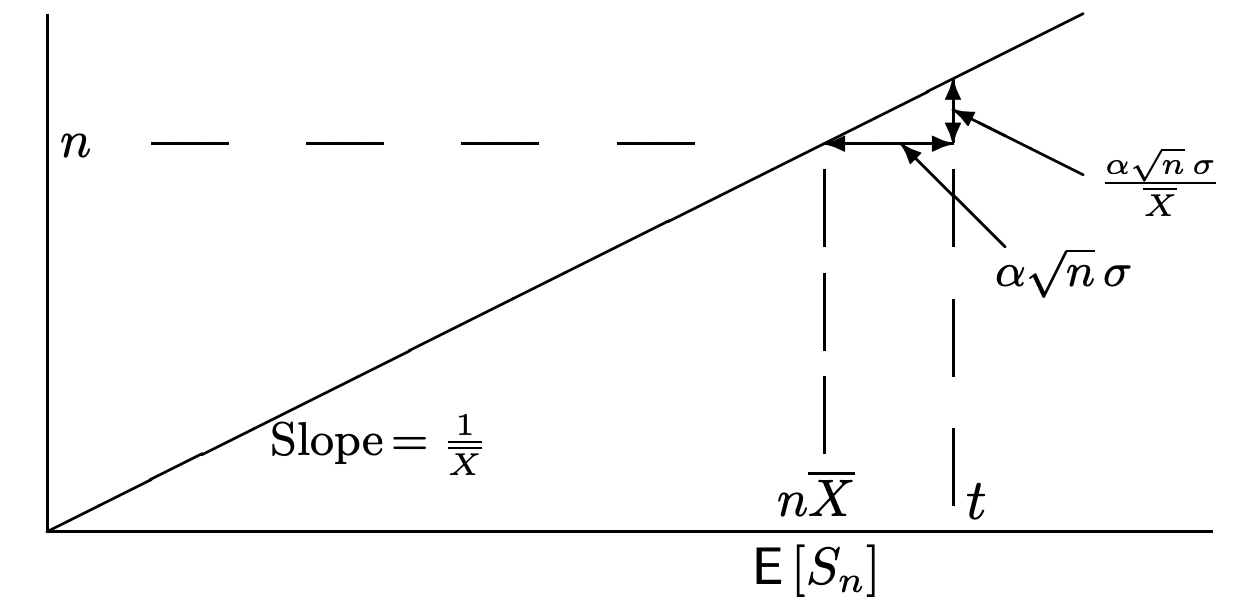
El teorema se puede probar aplicando el Teorema 1.5.2 (el CLT para una suma de IID rv)\(S_{n}\) y luego usando la identidad\(\left\{S_{n} \leq t\right\}=\{N(t) \geq n\}\). La idea general se ilustra en la Figura 4.4, pero los detalles son algo tediosos, y se pueden encontrar, por ejemplo, en [16]. Simplemente esbozamos el argumento aquí. De verdad\(\alpha\), el CLT afirma que

\(\operatorname{Pr}\left\{S_{n} \leq n \bar{X}+\alpha \sqrt{n} \sigma\right\} \approx \Phi(\alpha)\),

donde