4.4: Procesos de Renovación-Recompensa y Promedios de Tiempo

Hay muchas situaciones en las que, junto con un proceso de conteo de renovación$\{N(t) ; t>0\}$, hay otra función del tiempo que varía aleatoriamente, llamada función de recompensa$\{R(t) ; t>0\}$. $R(t)$modela una tasa a la que el proceso está acumulando una recompensa. Ilustraremos muchos ejemplos de tales procesos y veremos que una “recompensa” también podría ser un costo o cualquier cantidad de interés que varíe aleatoriamente. La restricción importante sobre estas funciones de recompensa es que$R(t)$ en un determinado$t$ depende únicamente de la ubicación de$t$ dentro del intervalo inter-renovación que contiene$t$ y quizás otras variables aleatorias locales a ese intervalo. Antes de definir esto precisamente, comenzamos con varios ejemplos.

Ejemplo 4.4.4 (Vida residual promedio en el tiempo)

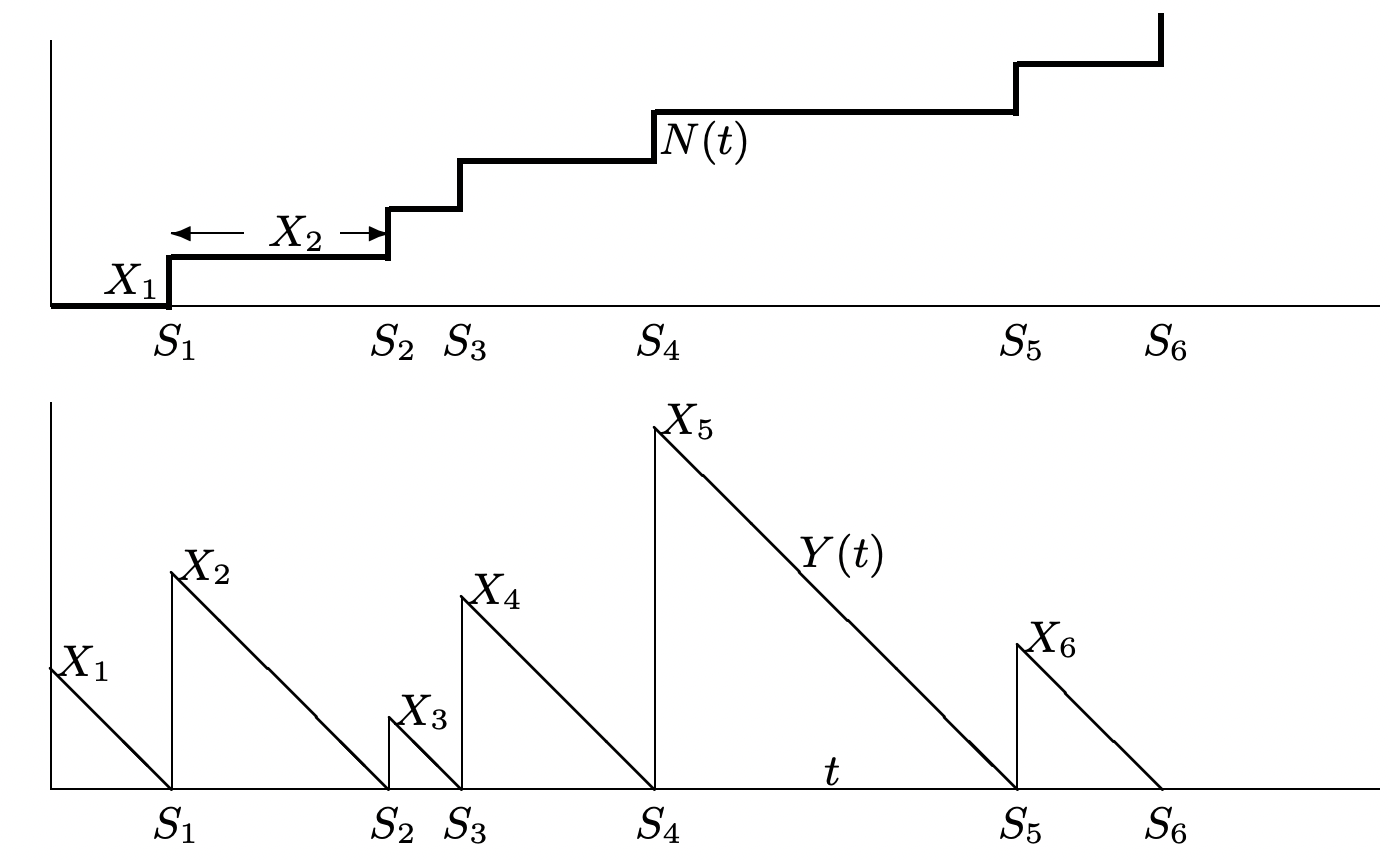
Para un proceso de conteo de renovación$\{N(t), t>0\}$, deja$Y(t)$ ser la vida residual en el momento$t$. La vida residual se define como el intervalo desde$t$ hasta la siguiente época de renovación, es decir, como$S_{N(t)+1}-t$. Por ejemplo, si llegamos a una parada de autobús a la hora$t$ y los autobuses llegan de acuerdo a un proceso de renovación,$Y(t)$ es el tiempo que tenemos que esperar a que llegue un autobús (ver Figura 4.5). Interpretamos$\{Y(t) ; t \geq 0\}$ como una función de recompensa. El promedio de tiempo de$Y(t)$, a lo largo del intervalo$(0, t]$, viene dado por ⁵$(1 / t) \int_{0}^{t} Y(\tau) d \tau$. Nos interesa el límite de esta media como$t \rightarrow \infty$ (asumiendo que existe en algún sentido). La Figura 4.5 ilustra una función de muestra de un proceso de recuento de renovación$\{N(t) ; t>0\}$ y muestra la vida residual$Y(t)$ para esa función de muestra. Tenga en cuenta que, para una función de muestra dada$\{Y(t)=y(t)\}$, la integral$\int_{0}^{t} y(\tau) d \tau$ es simplemente una suma de triángulos rectos isósceles, con parte de un triángulo final al final. Por lo tanto, se puede expresar como

$\int_{0}^{t} y(\tau) d \tau=\frac{1}{2} \sum_{i=1}^{n(t)} x_{i}^{2}+\int_{\tau=s_{n(t)}}^{t} y(\tau) d \tau$

donde$\left\{x_{i} ; 0<i<\infty\right\}$ es el conjunto de valores de muestra para los intervalos entre renovaciones.

Dado que esta relación se mantiene para cada punto de muestra, vemos que la variable aleatoria se$\int_{0}^{t} Y(\tau) d \tau$ puede expresar en términos de las variables aleatorias entre renovaciones$X_{n}$ como

$\int_{\tau=0}^{t} Y(\tau) d \tau=\frac{1}{2} \sum_{n=1}^{N(t)} X_{n}^{2}+\int_{\tau=S_{N(t)}}^{t} Y(\tau) d \tau$

Figura 4.5: Vida residual en el tiempo$t$. Para cualquier función muestral dada del proceso de renovación, la función muestral de vida residual disminuye linealmente con una pendiente de −1 desde el principio hasta el final de cada intervalo inter-renovación.

Si bien el término final anterior puede evaluarse fácilmente para un determinado$S_{N(t)}(t)$, es más conveniente utilizar el siguiente encuadernado:

$$\frac{1}{2 t} \sum_{n=1}^{N(t)} X_{n}^{2} \leq \frac{1}{t} \int_{\tau=0}^{t} Y(\tau) d \tau \leq \frac{1}{2 t} \sum_{n=1}^{N(t)+1} X_{n}^{2}\label{4.11}$$

El término de la izquierda ahora se puede evaluar en el límite$t \rightarrow \infty$ (para todas las funciones de muestra excepto un conjunto de probabilidad cero) de la siguiente manera:

$$\lim _{t \rightarrow \infty} \frac{\sum_{n=1}^{N(t)} X_{n}^{2}}{2 t}=\lim _{t \rightarrow \infty} \frac{\sum_{n=1}^{N(t)} X_{n}^{2}}{N(t)} \frac{N(t)}{2 t}\label{4.12}$$

Considere cada término en el lado derecho de\ ref {4.12} por separado. Para el primer término, recordemos que$\lim _{t \rightarrow 0} N(t)=\infty$ con probabilidad 1. Así como$t \rightarrow \infty$,$\sum_{n=1}^{N(t)} X_{n}^{2} / N(t)$ pasa por el mismo conjunto de valores que$\sum_{n=1}^{k} X_{n}^{2} / k$ as$k \rightarrow \infty$. Así, utilizando el SLLN,

$\lim _{t \rightarrow \infty} \frac{\sum_{n=1}^{N(t)} X_{n}^{2}}{N(t)}=\lim _{k \rightarrow \infty} \frac{\sum_{n=1}^{k} X_{n}^{2}}{k}=\mathrm{E}\left[X^{2}\right] \quad \text{WP1}$,

El segundo término en el lado derecho de\ ref {4.12} es simplemente$N(t) / 2 t$. Por la fuerte ley para procesos de renovación,$\lim _{t \rightarrow \infty} N(t) / 2 t=1 /(2 \mathrm{E}[X])$ WP1. Así existen ambos límites WP1 y

$$\lim _{t \rightarrow \infty} \frac{\sum_{n=1}^{N(t)} X_{n}^{2}}{2 t}=\frac{\mathrm{E}\left[X^{2}\right]}{2 \mathrm{E}[X]}\quad \text{WP1}\label{4.13}$$

El término derecho de\ ref {4.11} se maneja casi de la misma manera:

$$\lim _{t \rightarrow \infty} \frac{\sum_{n=1}^{N(t)+1} X_{n}^{2}}{2 t}=\lim _{t \rightarrow \infty} \frac{\sum_{n=1}^{N(t)+1} X_{n}^{2}}{N(t)+1} \frac{N(t)+1}{N(t)} \frac{N(t)}{2 t}=\frac{\mathrm{E}\left[X^{2}\right]}{2 \mathrm{E}[X]}\label{4.14}$$

Combinando estos dos resultados, vemos que, con probabilidad 1, la vida residual promedio en el tiempo viene dada por

$$\lim _{t \rightarrow \infty} \frac{\int_{\tau=0}^{t} Y(\tau) d \tau}{t}=\frac{\mathrm{E}\left[X^{2}\right]}{2 \mathrm{E}[X]}\label{4.15}$$

Tenga en cuenta que este promedio de tiempo depende del segundo momento de$X$; esto es$\bar{X}^{2}+\sigma^{2} \geq \bar{X}^{2}$, por lo que la vida residual promedio en el tiempo es al menos la mitad del intervalo esperado entre renovaciones (lo cual no es sorprendente). Por otro lado, el segundo momento de$X$ puede ser arbitrariamente grande (incluso infinito) para cualquier valor dado de$\mathrm{E}[X]$, de manera que la vida residual promedio en el tiempo puede ser arbitrariamente grande en relación con$\mathrm{E}[X]$. Esto se puede explicar intuitivamente observando que los intervalos interrenovaciones grandes se ponderan más fuertemente en este promedio de tiempo que los intervalos pequeños entre renovaciones.

Ejemplo 4.4.2

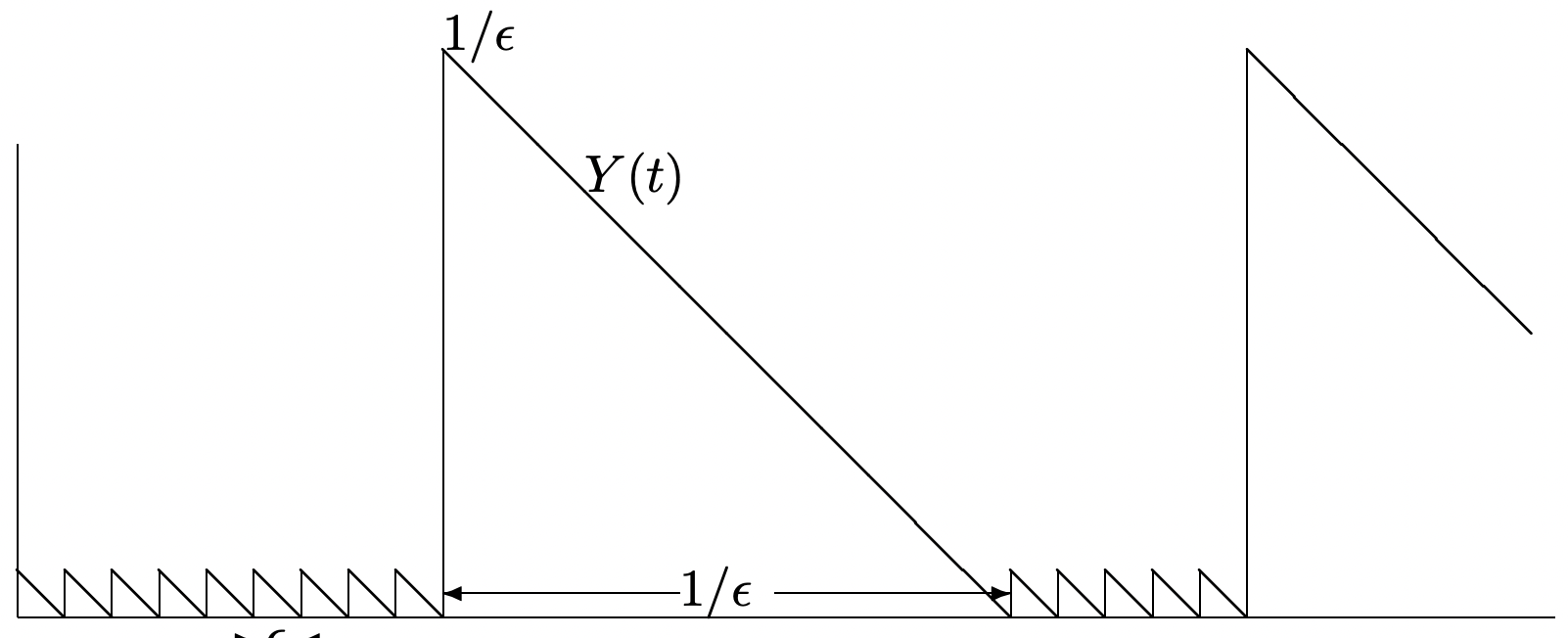
Como ejemplo del efecto de intervalos interrenovatorios improbables pero grandes, vamos$X$ a tomar el valor$\epsilon$ con probabilidad$1-\epsilon$ y valor$1 / \epsilon$ con probabilidad$\epsilon$. Entonces, para pequeños$\epsilon$,$\mathrm{E}[X] \sim 1, \mathrm{E}\left[X^{2}\right] \sim 1 / \epsilon$, y el tiempo promedio de vida residual es aproximadamente$1 /(2 \epsilon)$ (ver Figura 4.6).

Figura 4.6: La vida residual promedio está dominada por grandes intervalos entre llegadas. Cada intervalo grande tiene duración$1 / \epsilon$, y la duración agregada esperada entre intervalos grandes sucesivos es$1-\epsilon$

Ejemplo 4.4.3. (temporizador-promedio Edad)

Dejar$Z(t)$ ser la edad de un proceso de renovación en el momento en$t$ que la edad se define como el intervalo desde la llegada más reciente antes (o en)$t$ hasta$t$, es decir,$Z(t)=t-S_{N(t)}$. Por convención, si no se han producido llegadas por tiempo$t$, tomamos la edad para ser$t$ (es decir, en este caso,$N(t)=0$ y tomamos$S_{0}$ para ser 0).

Como se ve en la Figura 4.16, el proceso de edad, para una función de muestra dada del proceso de renovación, es casi el mismo que el proceso de vida residual: los triángulos rectos isósceles simplemente se dan la vuelta. Así, se puede utilizar el mismo análisis que antes para demostrar que el promedio de tiempo de$Z(t)$ es el mismo que el promedio de tiempo de la vida residual,

$$\lim _{t \rightarrow \infty} \frac{\int_{\tau=0}^{t} Z(\tau) d \tau}{t}=\frac{\mathrm{E}\left[X^{2}\right]}{2 \mathrm{E}[X]} \quad\text{WP1}\label{4.16}$$

Figura 4.7: Edad en el momento$t$: Para cualquier función muestral dada del proceso de renovación, la función muestral de edad aumenta linealmente con una pendiente de 1 desde el inicio hasta el final de cada intervalo inter-renovación.

Ejemplo 4.4.4. (Duración promedio de tiempo)

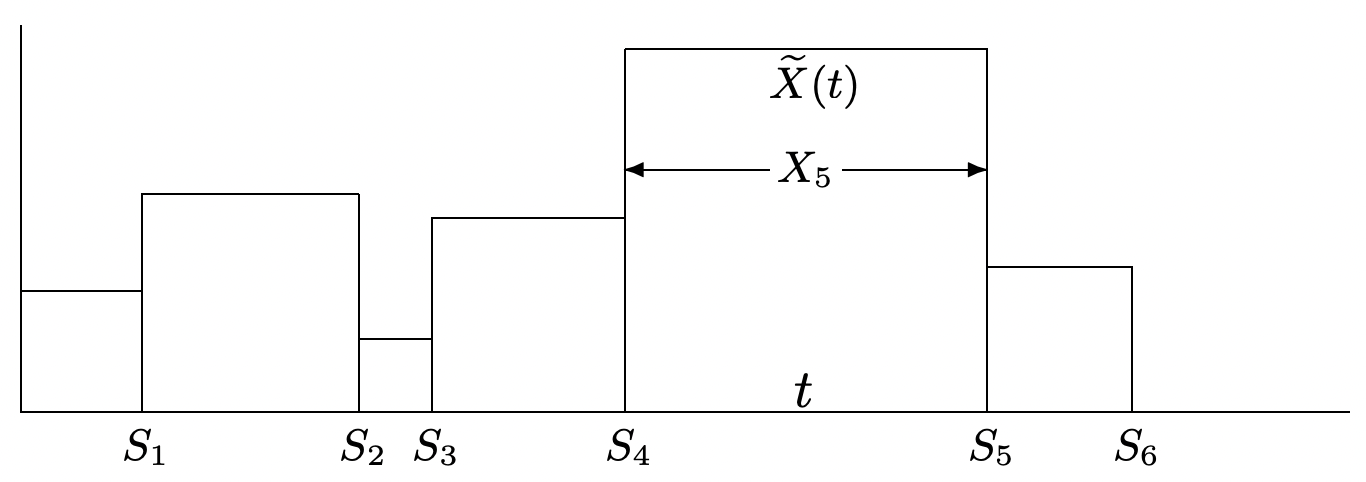
$\widetilde{X}(t)$Sea la duración del intervalo entre renovaciones que contiene el tiempo$t$, es decir,$\widetilde{X}(t)=X_{N(t)+1}=S_{N(t)+1}-S_{N(t)}$ (ver Figura 4.8). Es claro que$\widetilde{X}(t)=Z(t)+Y(t)$, y así el promedio de tiempo de la duración viene dado por

$$\lim _{t \rightarrow \infty} \frac{\int_{\tau=0}^{t} \widetilde{X}(\tau) d \tau}{t}=\frac{\mathrm{E}\left[X^{2}\right]}{\mathrm{E}[X]}\text{WP1}\label{4.17}$$

Nuevamente, los intervalos largos están fuertemente ponderados en este promedio, de manera que la duración promedio de tiempo es al menos tan grande como el intervalo medio entre renovaciones y a menudo mucho más grande.

Figura 4.8: Duración$\widetilde{X}(t)=X_{N(t)}$ del intervalo inter-renovación que contiene$t$.

Procesos generales de renovación-recompensa

En cada uno de estos ejemplos, y en muchas otras situaciones, tenemos una función aleatoria del tiempo (es decir,,$Y(t)$$Z(t)$, o$\tilde{X}(t)$) cuyo valor en el tiempo$t$ depende únicamente de dónde$t$ se encuentre en el intervalo interrenovador actual (es decir, de la edad$Z(t)$ y la duración$\widetilde{X}(t)$ del intervalo entre renovaciones actuales). Ahora investigamos la clase general de funciones de recompensa para las cuales la recompensa en el momento$t$ depende como máximo de la edad y la duración en$t$, es decir, la recompensa$R(t)$ en el momento$t$ se da explícitamente como una función ⁶$\mathcal{R}(Z(t), \widetilde{X}(t))$ de la edad y duración en$t$.

Para los tres ejemplos anteriores, la función$\mathcal{R}$ es trivial. Es decir, la vida residual,$Y(t)$, viene dada por$\widetilde{X}(t)-Z(t)$ y la edad y duración se dan directamente.

Ahora encontramos el valor promedio de tiempo de$R(t)$, es decir,$\lim _{t \rightarrow \infty} \frac{1}{t} \int_{0}^{t} R(\tau) d \tau$. Al igual que en los ejemplos t 0 4.4.1 a 4.4.4 anteriores, primero queremos ver la recompensa acumulada en cada periodo inter-renovación por separado. Definir$\mathrm{R}_{n}$ como la recompensa acumulada en el enésimo intervalo de renovación,

$$\mathrm{R}_{n}=\int_{S_{n-1}}^{S_{n}} R(\tau) d(\tau)=\int_{S_{n-1}}^{S_{n}} \mathcal{R}[Z(\tau), \widetilde{X}(\tau)] d \tau\label{4.18}$$

Para la vida residual (ver Ejemplo 4.4.1),$\mathrm{R}_{n}$ es el área del enésimo triángulo rectángulo isósceles en la Figura 4.5. En general, ya que$Z(\tau)=\tau-S_{n-1}$,

$$\mathrm{R}_{n}=\int_{S_{n-1}}^{S_{n}} \mathcal{R}\left(\tau-S_{n-1}, X_{n}\right) d \tau=\int_{z=0}^{X_{n}} \mathcal{R}\left(z, X_{n}\right) d z\label{4.19}$$

Tenga en cuenta que$\mathrm{R}_{n}$ es una función solamente de$X_{n}$, donde la forma de la función está determinada por$\mathcal{R}(Z, X)$. A partir de esto, queda claro que$\left\{\mathrm{R}_{n} ; n \geq 1\right\}$ es esencialmente ⁷ un conjunto de variables aleatorias IID. Para la vida residual,$\mathcal{R}\left(z, X_{n}\right)=X_{n}-z$, por lo que la integral en\ ref {4.19} es$X_{n}^{2} / 2$, según se calculó por inspección antes. En general, a partir de (4.19), el valor esperado de$\mathrm{R}_{n}$ viene dado por

$$\mathrm{E}\left[\mathrm{R}_{n}\right]=\int_{x=0}^{\infty} \int_{z=0}^{x} \mathcal{R}(z, x) d z\ d \mathrm{~F}_{X}(x)\label{4.20}$$

Al$\int_{0}^{t} R(\tau) d \tau$ irrumpir en la recompensa durante los sucesivos períodos de renovación, obtenemos

\ [\ begin {alineado}
\ int_ {0} ^ {t} R (\ tau) d\ tau &=\ int_ {0} ^ {S_ {1}} R (\ tau) d\ tau+\ int_ {S_ {1}} ^ {S_ {2}} R (\ tau) d\ tau+\ cdots+\ int_ {S_ {N (t) -1}} ^ {S_ {N (t)}} R (\ tau) d\ tau+\ int_ {S_ {N (t)}} ^ {t} R (\ tau) d\ tau\
&=\ sum_ {n=1} ^ {N (t)}\ mathrm {R} _ _ {n} +\ int_ {S_ {N (t)}} ^ {t} (\ tau) d\ tau
\ end {alineado}\ etiqueta {4.21}\]

El siguiente teorema ahora generaliza los resultados de los Ejemplos 4.4.1, 4.4.3 y 4.4.4 a las funciones generales de renovación-recompensa.

Teorema 4.4.1

Dejar$\{R(t) ; t>0\} \geq 0$ ser una función de renovación-recompensa no negativa para un proceso de renovación con tiempo esperado entre renovaciones$\mathrm{E}[X]=\bar{X}<\infty$. Si$E\left[R_{n}\right]<\infty$, entonces con probabilidad 1

$$\lim _{t \rightarrow \infty} \frac{1}{t} \int_{\tau=0}^{t} R(\tau) d \tau=\frac{\mathrm{E}\left[\mathrm{R}_{n}\right]}{\bar{X}}\label{4.22}$$

Prueba

Usando (4.21), la recompensa acumulada hasta el tiempo se$t$ puede limitar entre la recompensa acumulada hasta la renovación anterior$t$ y aquella hasta la siguiente renovación posterior$t$,

$$\frac{\sum_{n=1}^{N(t)} \mathrm{R}_{n}}{t} \leq \frac{\int_{\tau=0}^{t} R(\tau) d \tau}{t} \leq \frac{\sum_{n=1}^{N(t)+1} \mathrm{R}_{n}}{t}\label{4.23}$$

El lado izquierdo de\ ref {4.23} ahora se puede romper en

$$\frac{\sum_{n=1}^{N(t)} \mathrm{R}_{n}}{t}=\frac{\sum_{n=1}^{N(t)} \mathrm{R}_{n}}{N(t)} \frac{N(t)}{t}\label{4.24}$$

Cada uno$\mathrm{R}_{n}$ es una función dada de$X_{n}$, por lo que los$\mathrm{R}_{n}$ son IID. Como$t \rightarrow \infty$,$N(t) \rightarrow \infty$, y, así, como hemos visto antes, la fuerte ley de los números grandes se puede utilizar en el primer término del lado derecho de (4.24), obteniendo$\mathrm{E}\left[\mathrm{R}_{n}\right]$ con probabilidad 1. También el segundo término se acerca$1 / \bar{X}$ por la ley fuerte para los procesos de renovación. Dado que$0<\bar{X}<\infty$ y$\mathrm{E}\left[\mathrm{R}_{n}\right]$ es finito, el producto de los dos términos se acerca al límite$\mathrm{E}\left[\mathrm{R}_{n}\right] / \bar{X}$. La desigualdad de la mano derecha de\ ref {4.23} se maneja casi de la misma manera,

$$\frac{\sum_{n=1}^{N(t)+1} \mathrm{R}_{n}}{t}=\frac{\sum_{n=1}^{N(t)+1} \mathrm{R}_{n}}{N(t)+1} \frac{N(t)+1}{N(t)} \frac{N(t)}{t}\label{4.25}$$

Se ve que los términos del lado derecho de\ ref {4.25} se acercan a los límites como antes y así el término de la izquierda se acerca $$\mathrm{E}\left[\mathrm{R}_{n}\right] / \bar{X} \nonumber$$ con probabilidad 1. Dado que el límite superior e inferior en\ ref {4.23} se acercan al mismo límite,$(1 / t) \int_{0}^{t} R(\tau) d \tau$ se acerca al mismo límite y se prueba el teorema.

La restricción a las funciones de renovación-recompensa no negativas en el Teorema 4.4.1 es ligeramente artificial. El mismo resultado se aplica para las funciones de recompensa no positivas simplemente cambiando las direcciones de las desigualdades en (4.23). Suponiendo que eso$\mathrm{E}\left[\mathrm{R}_{n}\right]$ existe (es decir, que tanto sus partes positivas como negativas son finitas), el mismo resultado se aplica en general dividiendo una función de recompensa arbitraria en una parte positiva y negativa. Esto nos da el corolario:

Corolario 4.4.1

Let$\{R(t) ; t>0\}$ Ser una función de renovación-recompensa para un proceso de renovación con tiempo esperado entre renovaciones$\mathrm{E}[X]=\bar{X}<\infty$. Si$\mathrm{E}\left[\mathrm{R}_{n}\right]$ existe, entonces con probabilidad 1

$$\lim _{t \rightarrow \infty} \frac{1}{t} \int_{\tau=0}^{t} R(\tau) d \tau=\frac{\mathrm{E}\left[\mathrm{R}_{n}\right]}{\bar{X}}\label{4.26}$$

Ejemplo 4.4.5 (Distribución de la Vida Residual)

El Ejemplo 4.4.1 trató el valor promedio de tiempo de la vida residual$Y(t)$. Supongamos, sin embargo, que nos gustaría encontrar la función de distribución de tiempo promedio de$Y(t)$, es decir, la fracción de tiempo$Y(t) \leq y$ que en función de$y$. El enfoque, que se aplica a una amplia variedad de aplicaciones, es utilizar una función de indicador (para un valor dado de$y$) como función de recompensa. Es decir, definir$R(t)$ tener el valor 1 para todos$t$ tales que$Y(t) \leq y$ y tener el valor 0 en caso contrario. La Figura 4.9 ilustra esta función para una ruta de muestra dada. Expresando esta función de recompensa en términos de$Z(t)$ y$\widetilde{X}(t)$, tenemos

$R(t)=\mathcal{R}(Z(t), \widetilde{X}(t))= \begin{cases}1 ; & \tilde{X}(t)-Z(t) \leq y \\ 0 ; & \text { otherwise }\end{cases}$

Tenga en cuenta que si un intervalo entre renovaciones es menor que$y$ (como el tercer intervalo en la Figura 4.9), entonces$R(t)$ tiene el valor uno sobre todo el intervalo, mientras que si el intervalo es mayor

Figura 4.9: Función de recompensa para encontrar la fracción de tiempo promedio de tiempo que$\{Y(t) \leq y\}$. Para la función de muestra en la figura,$X_{1}>y, X_{2}>y$, y$X_{4}>y$, pero$X_{3}<y$

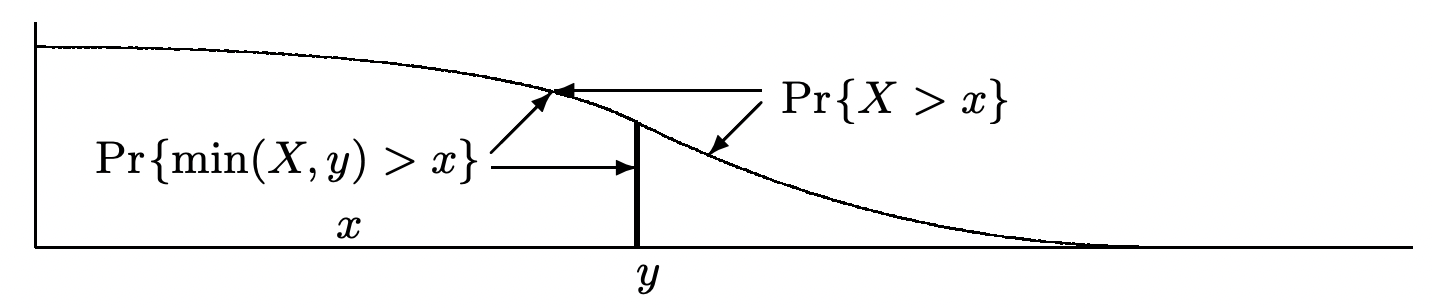
que$y$, entonces$R(t)$ tiene el valor uno solo sobre las$y$ unidades finales del intervalo. Así$\mathrm{R}_{n}=\min \left[y, X_{n}\right]$. Tenga en cuenta que la variable aleatoria$\min \left[y, X_{n}\right]$ es igual a$X_{n}$ for$X_{n} \leq y$, y por lo tanto tiene la misma función de distribución que$X_{n}$ en el rango 0 a$y$. La Figura 4.10 ilustra esto en términos de la función de distribución complementaria. De la figura, vemos que

$$\mathrm{E}\left[\mathrm{R}_{n}\right]=\mathrm{E}[\min (X, y)]=\int_{x=0}^{\infty} \operatorname{Pr}\{\min (X, y)>x\} d x=\int_{x=0}^{y} \operatorname{Pr}\{X>x\} d x\label{4.27}$$

Figura 4.10:$\mathrm{R}_{n}$ para distribución de la vida residual.

Dejar$\mathrm{F}_{Y}(y)=\lim _{t \rightarrow \infty}(1 / t) \int_{0}^{t} R(\tau) d \tau$ denotar la fracción de tiempo promedio de tiempo que la vida residual es menor o igual a$y$. Del Teorema 4.4.1 y la Eq. (4.27), tenemos entonces

$$\mathrm{F}_{Y}(y)=\frac{\mathrm{E}\left[\mathrm{R}_{n}\right]}{\bar{X}}=\frac{1}{\bar{X}} \int_{x=0}^{y} \operatorname{Pr}\{X>x\} d x \quad \mathrm{WP} 1\label{4.28}$$

Como cheque, tenga en cuenta que esta integral está aumentando en$y$ y se acerca a 1 como$y \rightarrow \infty$. Obsérvese también que el valor esperado de$Y$, calculado a partir de (4.28), viene dado por$\mathrm{E}\left[X^{2}\right] / 2 \bar{X}$, de acuerdo con (4.15).

El mismo argumento se puede aplicar a la distribución tiempo-promedio de la edad (ver Ejercicio 4.12). La fracción de tiempo promedio de tiempo$\mathrm{F}_{Z}(z)$,, que la edad es como máximo$z$ viene dada por

$$\mathrm{F}_{Z}(z)=\frac{1}{\bar{X}} \int_{x=0}^{z} \operatorname{Pr}\{X>x\} d x \quad{WP1}\label{4.29}$$

En el desarrollo hasta el momento, la función de recompensa$R(t)$ ha sido una función únicamente de los intervalos de edad y duración, y la recompensa agregada sobre el enésimo intervalo inter-renovación es una función únicamente de$X_{n}$. En situaciones más generales, donde el proceso de renovación está incrustado en algún proceso más complejo, a menudo es deseable definir$R(t)$ depender de otros aspectos del proceso también. Lo importante aquí es$\left\{\mathrm{R}_{n} ; n \geq 1\right\}$ que sea una secuencia IID. En la Sección 4.5.3 se describe cómo lograrlo y cómo se relaciona con los sistemas de colas. Teorema 4.4.1 claramente sigue siendo válido si$\left\{\mathrm{R}_{n} ; n \geq 1\right\}$ es IID. Este tipo más general de función de renovación-recompensa será requerido y discutido más a fondo en las Secciones 4.5.3 a Rss7 donde discutimos el teorema de Little y el retraso de cola esperado M/G/1, ambos utilizan esta estructura más general.

Los promedios de tiempo limitantes a veces se visualizan mediante el siguiente tipo de experimento. Para algunos dado gran tiempo$t$, dejar$T$ ser una variable aleatoria uniformemente distribuida sobre$(0, t]$;$T$ es independiente del proceso de renovación-recompensa bajo consideración. Entonces$(1 / t) \int_{0}^{t} R(\tau) d \tau$ es el valor esperado (sobre$T$) de$R(T)$ para una ruta de muestra dada de$\{R(\tau) ; \tau>0\}$. El teorema 4.4.1 establece que en el límite$t \rightarrow \infty$, todas las rutas de muestreo (excepto un conjunto de probabilidad 0) arrojan el mismo valor esperado sobre$T$. Este enfoque de ver un promedio de tiempo como una elección aleatoria de tiempo se conoce como incidencia aleatoria. La incidencia aleatoria es incómoda matemáticamente, ya que la variable aleatoria$T$ cambia con el tiempo general$t$ y no tiene límite razonable. También difumina la distinción entre tiempo y ensemble-promedios, por lo que no se utilizará en lo que sigue.

---

⁵$\int_{0}^{t} Y(\tau) d \tau$ es un rv como cualquier otra función de un conjunto de rv. Tiene un valor de muestra para cada función de muestra de$\{N(t) ; t>0\}$, y su función de distribución podría calcularse de una manera sencilla pero tediosa. Para procesos estocásticos arbitrarios, la integración y diferenciación pueden requerir una gran sofisticación matemática, pero ninguna de esas sutilezas se presenta aquí.

⁶ Esto significa que se$R(t)$ puede determinar en cualquiera$t$ de conocer$Z(t)$ y$X(t)$. No quiere decir que$R(t)$ deba variar ya que se cambia cualquiera de esas cantidades. Así, por ejemplo,$R(t)$ podría depender de solo uno de los dos o incluso podría ser una constante.

⁷ Ciertamente se pueden definir funciones$\mathcal{R}(Z, X)$ para las cuales la integral en\ ref {4.19} es infinita o indefinida para algunos valores de$X_{n}$, y así$\mathrm{R}_{n}$ se convierte en una rv defectuosa. Parece mejor manejar este tipo de situaciones cuando surge en lugar de manejarla en general.