4.5: Pruebas de detención aleatoria

Visualizar realizando un experimento repetidamente, observando salidas de muestra sucesivas independientes de una variable aleatoria dada (es decir, observando un resultado de muestra de\(X_{1}, X_{2}, \ldots\) donde\(X_{i}\) están IID). El experimento se detiene cuando se han acumulado suficientes datos para los fines en cuestión.

Este tipo de situación ocurre con frecuencia en las aplicaciones. Por ejemplo, podríamos estar obligados a elegir entre varias hipótesis, y podríamos repetir un experimento hasta que las hipótesis sean suficientemente discriminadas. Si se permite que el número de ensayos dependa del resultado, el número medio de ensayos requeridos para lograr una probabilidad de error dada suele ser una pequeña fracción del número de ensayos requeridos cuando el número se elige de antemano. Otro ejemplo ocurre en las búsquedas de árboles donde se explora un camino hasta que otras extensiones del camino parecen no ser rentables.

El primer estudio cuidadoso de situaciones experimentales donde el número de ensayos depende de los datos fue realizado por el estadístico Abraham Wald y condujo al campo del análisis secuencial (ver [21]). Estudiamos estas situaciones ahora ya que uno de los principales resultados, la igualdad de Wald, será útil para estudiar\(\mathrm{E}[N(t)]\) en la siguiente sección. La detención de ensayos suele ser útil en el estudio de procesos aleatorios, y en particular se utilizará en la Sección 4.7 para el análisis de colas, y nuevamente en el Capítulo 7 como temas centrales en el estudio de Caminatas aleatorias y martingales.

Una parte importante de los experimentos que se detienen después de un número aleatorio de ensayos es la regla para detenerse. Dicha regla debe especificar, para cada ruta de muestreo, el ensayo en el que se detiene el experimento, es decir, el juicio final después del cual no se realizan más ensayos. Por lo tanto, la regla para detener debe especificar una variable aleatoria positiva, de valor entero\(J\), llamada tiempo de detención, o detención de prueba, mapeando rutas de muestra a este ensayo final en el que se detiene el experimento.

Consideramos que el espacio muestral incluye el conjunto de secuencias de valores de muestra para la secuencia interminable de variables aleatorias\(X_{1}, X_{2}, \ldots\). Es decir, aunque el experimento se detenga al final del segundo ensayo, aún se visualizan las variables aleatorias 3º, 4º,. como que tienen valores de muestra como parte de la función de muestra. Es decir, visualizamos que el experimento continúa para siempre, pero que el observador deja de mirar al final del punto de parada. Desde el punto de vista de las aplicaciones, el experimento podría o no continuar después de que el observador deje de mirar. Desde un punto de vista matemático, sin embargo, es muy preferible ver el experimento como continuo. Esto evita confusión y ambigüedad sobre el significado de IID rv cuando la existencia misma de variables posteriores depende de valores de muestra anteriores.

La noción intuitiva de detener un experimento secuencial debe implicar detenerse en función de los datos (es decir, los valores de la muestra) recopilados hasta e incluyendo el punto de parada. Por ejemplo, si\(X_{1}, X_{2}, \ldots\), representan los cambios sucesivos en nuestra fortuna al apostar, es posible que queramos detenernos cuando nuestra ganancia acumulada supere algún valor fijo. El ensayo de detención\(n\) entonces depende de los valores de muestra de\(X_{1}, X_{2}, \ldots, X_{n}\). Al mismo tiempo, queremos excluir de detener los ensayos aquellas reglas que permitan al experimentador echar un vistazo a los valores posteriores antes de tomar la decisión de detenerse o no. ⁸ Esto lleva a la siguiente definición.

Definición 4.5.1

Un ensayo de detención (o tiempo de detención ⁹) J para una secuencia de rv\(X_{1}, X_{2}, \ldots\), es un rv de valor entero positivo tal que para cada uno\(n \geq 1\), el indicador rv\(\mathbb{I}_{\{J=n\}}\) es una función de\(\left\{X_{1}, X_{2}, \ldots, X_{n}\right\}\).

La última cláusula de la definición significa que cualquier valor de muestra dado\(x_{1}, \ldots, x_{n}\) para determina de\(X_{1}, \ldots, X_{n}\) manera única si el valor de muestra correspondiente de\(J\) se define como un rv de valor entero positivo, los eventos\(\{J=n\}\) y\(\{J=m\}\) para\(m<n\) son eventos disjuntos, por lo que se detiene en el juicio \(m\)hace imposible detenerse también en\(n\) para una ruta de muestra dada. También la unión de los eventos\(\{J=n\}\) sobre\(n \geq 1\) tiene probabilidad 1. Aparte de esta restricción final, la definición no depende de la medida de probabilidad y depende únicamente del conjunto de eventos\(\{J=n\}\) para cada uno\(n\). En muchas situaciones, es útil relajar aún más la definición\(J\) para permitir que sea un rv posiblemente defectuoso. En este caso la cuestión de si la detención ocurre con probabilidad 1 puede posponerse hasta después de especificar los eventos disjuntos\(\{J=n\}\) terminados\(n \geq 1\).

Ejemplo 4.5.1

Considera un proceso de Bernoulli\(\left\{X_{n} ; n \geq 1\right\}\). Una prueba de detención muy simple para este proceso es detenerse en la primera aparición de la cadena (1, 0). La Figura 4.11 ilustra este ensayo de detención viéndolo como un truncamiento del árbol de posibles secuencias binarias.

El evento\(\{J=2\}\), es decir, el evento que se detiene ocurre en el juicio 2, es el evento\(\left\{X_{1}=1, X_{2}=0\right\}\). De igual manera, el evento\(\{J=3\}\) es\(\left\{X_{1}=1, X_{2}=1, X_{3}=0\right\} \bigcup\left\{X_{1}=0, X_{2}=1, X_{3}=0\right\}\). La desarticulación de\(\{J=n\}\) y\(\{J=m\}\) para\(n \neq m\) se representa en la figura terminando el árbol en cada nodo de parada. Se puede ver que el árbol nunca muere por completo, y de hecho, para cada prueba\(n\), el número de nodos de detención es\(n-1\). Sin embargo, la probabilidad de que la detención no haya ocurrido por ensayo\(n\) va a cero exponencialmente con\(n\), lo que asegura que\(J\) es una variable aleatoria.

Figura 4.11: Un árbol que representa el conjunto de secuencias binarias, con una regla de parada vista como una poda del árbol. La regla particular de detención aquí es detenerse en la primera aparición de la cadena (1, 0). Las hojas del árbol (es decir, los nodos en los que se produce la detención) están marcadas con puntos grandes y los nodos intermedios (los otros nodos) con puntos pequeños. Tenga en cuenta que cada hoja en el árbol tiene una correspondencia uno a uno con un segmento inicial del árbol, por lo que los nodos de detención pueden verse sin ambigüedades ya sea como hojas del árbol o segmentos iniciales de las secuencias de muestra.

La representación de una regla de detención por un árbol podado se puede utilizar para cualquier secuencia aleatoria discreta, aunque el árbol se vuelve bastante difícil de manejar en todos los casos menos triviales. Visualizar una regla de detención en términos de un árbol podado es útil conceptualmente, pero las reglas de detención generalmente se establecen en otros términos. Por ejemplo, en breve consideramos un juicio de detención para los intervalos entre llegadas de un proceso de renovación como el primero\(n\) para el cual la época de llegada\(S_{n}\) satisface\(S_{n}>t\) para algunos dados\(t>0\).

La igualdad de Wald

Una cuestión importante que surge con la detención de los ensayos es evaluar la suma\(S_{J}\) de las variables aleatorias hasta el ensayo de detención, es decir,\(S_{J}=\sum_{n=1}^{J} X_{n}\). Muchas estrategias de juego y estrategias de inversión implican algún tipo de regla sobre cuándo parar, y es importante entender el rv\(S_{J}\) (que puede modelar la ganancia o pérdida general hasta ese juicio). La igualdad de Wald es muy útil para ayudar a encontrar\(\mathrm{E}\left[S_{J}\right]\).

Teorema 4.5.1: La igualdad de Wald

Dejar\(\left\{X_{n} ; n \geq 1\right\}\) ser una secuencia de IID rv, cada uno de media\(\bar{X}\). Si\(J\) es un juicio de detención para\(\left\{X_{n} ; n \geq 1\right\}\) y si\(\mathrm{E}[J]<\infty\), entonces la suma\(S_{J}=X_{1}+X_{2}+\cdots+X_{J}\) en el juicio de detención\(J\) satisface

\[\mathrm{E}\left[S_{J}\right]=\bar{X} \mathrm{E}[J]\label{4.30} \]

Prueba

Tenga en cuenta que\(X_{n}\) se incluye en\(S_{J}=\sum_{n=1}^{J} X_{n}\) cuando\(n \leq J\), es decir, siempre que la función indicadora n=1\(\mathbb{I}_{\{J \geq n\}}=1\). Así

\[S_{J}=\sum_{n=1}^{\infty} X_{n} \mathbb{I}_{\{J \geq n\}}\label{4.31} \]

Esto incluye\(X_{n}\) como parte de la suma si la detención no ha ocurrido antes del juicio\(n\). El evento\(\{J \geq n\}\) es el complemento de\(\{J<n\}=\{J=1\} \bigcup \cdots \bigcup\{J=n-1\}\). Todos estos últimos eventos están determinados por\(X_{1}, \ldots, X_{n-1}\) y, por lo tanto, son independientes de\(X_{n}\). De ello se deduce que\(X_{n}\) y\(\{J<n\}\) son independientes y por lo tanto\(X_{n}\) y también\(\{J \geq n\}\) son independientes. ¹⁰ Así

\[\mathrm{E}\left[X_{n} \mathbb{I}_{\{J \geq n\}}\right]=\bar{X} \mathrm{E}\left[\mathbb{I}_{\{J \geq n\}}\right] \nonumber \]

Entonces tenemos

\ [\ begin {alineado}
\ mathrm {E}\ izquierda [S_ {J}\ derecha] &=\ mathrm {E}\ izquierda [\ sum_ {n=1} ^ {\ infty} X_ {n}\ mathbb {I} _ _ {\ {J\ geq n\}}\ derecha]\\
&=\ sum_ {n=1} ^ {\ infty}\ mathrm {E}\ izquierda [X_ {n}\ mathbb {I} _ {\ {J\ geq n\}}\ derecha]\ quad (4.32)\\
&=\ sum_ {n=1} ^ {\ infty}\ bar { X}\ mathrm {E}\ izquierda [\ mathbb {I} _ {\ {J\ geq n\}}\ derecha]\\
&=\ bar {X}\ mathrm {E} [J]. \ quad\ quad\ quad\ quad\ quad (4.33)
\ end {alineado}\ nonumber\]

El intercambio de expectativa y suma infinita en\ ref {4.32} es obviamente válido para una suma finita, y se muestra en el Ejercicio 4.18 como válido para una suma infinita si\(\mathrm{E}[J]<\infty\). El siguiente ejemplo muestra que la igualdad de Wald puede ser inválida cuando\(\mathrm{E}[J]=\infty\). El último paso anterior viene de la observación de que\(\mathrm{E}\left[\mathbb{I}_{\{J \geq n\}}\right]=\operatorname{Pr}\{J \geq n\}\). Dado que\(J\) es un número entero positivo rv,\(\mathrm{E}[J]=\sum_{n=1}^{\infty} \operatorname{Pr}\{J \geq n\}\). También se puede obtener el último paso utilizando\(J=\sum_{n=1}^{\infty} \mathbb{I}_{\{J \geq n\}}\) (ver Ejercicio 4.13).

Lo que este resultado esencialmente dice en términos de juego es que las estrategias para cuándo dejar de apostar no son realmente efectivas en lo que a la media se refiere. Esto a veces parece obvio y a veces parece muy sorprendente, dependiendo de la aplicación.

Ejemplo 4.5.2 (Detener cuando estés por delante en el lanzamiento de monedas).

Podemos modelar un juego de lanzamiento de monedas (sesgado) como una secuencia de IID rv\(X_{1}, X_{2}, \ldots\) donde cada uno\(X\) es 1 con probabilidad\(p\) y −1 con probabilidad\(1-p\). Considere el juicio de detención posiblemente defectuoso\(J\) donde\(J\) está el primero\(n\) para el cual\(S_{n}=X_{1}+\cdots+X_{n}=1\), es decir, el primer juicio en el que el jugador está por delante.

Primero queremos ver si\(J\) es un rv, es decir, si la probabilidad de una eventual parada, digamos\(\theta=\operatorname{Pr}\{J<\infty\}\), es 1. Esto lo resolvemos con un truco frecuentemente útil, pero usaremos otros enfoques más sistemáticos en los Capítulos 5 y 7 cuando veamos este mismo ejemplo como una cadena de Markov de nacimiento-muerte y luego como una simple caminata aleatoria. Obsérvese que\(\operatorname{Pr}\{J=1\}=p\), es decir,\(S_{1}=1\) con probabilidad\(p\) y parada ocurre en el ensayo 1. Con probabilidad\(1-p\),\(S_{1}=-1\). A continuación\(S_{1}=-1\), la única manera de llegar a ser uno adelante es volver primero a\(S_{n}=0\) para algunos\(n>1\), y, después del primer regreso de ese tipo, pasar a\(S_{m}=1\) en algún juicio posterior\(m\). La probabilidad de pasar eventualmente de -1 a 0 es la misma que la de ir de 0 a 1, es decir,\(\theta\). También, dado un primer retorno a 0 de -1, la probabilidad de llegar a 1 de 0 es\(\theta\). Por lo tanto,

\(\theta=p+(1-p) \theta^{2}\).

Esta es una ecuación cuadrática\(\theta\) con dos soluciones,\(\theta=1\) y\(\theta=p /(1-p)\). Porque\(p>1 / 2\), la segunda solución es imposible ya que\(\theta\) es una probabilidad. Así concluimos que\(J\) es un rv. Para\(p=1 / 2\) (y este es el caso más interesante), ambas soluciones son las mismas,\(\theta=1\), y de nuevo\(J\) es un rv. Para\(p<1 / 2\), la solución correcta ¹¹ es\(\theta=p /(1-p)\). \(\theta<1\)Así\(J\) es un rv defectuoso.

Para los casos donde\(p \geq 1 / 2\), es decir, donde\(J\) es un rv, podemos usar el mismo truco para evaluar\(\mathrm{E}[J]\),

\(\mathrm{E}[J]=p+(1-p)(1+2 \mathrm{E}[J])\)

La solución a esto es

\(\mathrm{E}[J]=\frac{1}{2(1-p)}=\frac{1}{2 p-1}\)

Vemos que\(\mathrm{E}[J]\) es finito para\(p>1 / 2\) e infinito para\(p=1 / 2\).

Pues\(p>1 / 2\), podemos comprobar que estos resultados concuerdan con la igualdad de Wald. En particular, ya que\(S_{J}\) es 1 con probabilidad 1, también tenemos\(\mathrm{E}\left[S_{J}\right]=1\). Desde\(\bar{X}=2 p-1\) y\(\mathrm{E}[J]=1 /(2 p-1)\), la igualdad de Wald está satisfecha (que por supuesto tiene que ser).

Para\(p=1 / 2\), todavía tenemos\(S_{J}=1\) con probabilidad 1 y así\(\mathrm{E}\left[S_{J}\right]=1\). Sin embargo\(\bar{X}=0\) así no\(\bar{X} \mathrm{E}[J]\) tiene sentido y la igualdad de Wald se rompe. Así vemos que efectivamente se necesita la restricción\(\mathrm{E}[J]<\infty\) en la igualdad de Wald. Estos resultados se tabulan a continuación.

\ (\ begin {array} {|r||ccc|}
& p>\ frac {1} {2} & p=\ frac {1} {2} & p<\ frac {1} {2}\
\ hline\ nombreoperador {Pr}\ {J<\ infty\} &\ frac {p} {1-p} & 1\\
\ mathrm {E} [J] &\ infty &\ infty &\ frac {1} {2 p-1}\\
\ hline
\ end {array}\)

Es sorprendente que con\(p=1 / 2\), el jugador eventualmente pueda convertirse en uno por delante con probabilidad 1. Esto tiene poco valor práctico, primero porque el número esperado requerido de ensayos es infinito, y segundo (como se verá más adelante) porque el jugador debe arriesgar un capital potencialmente infinito.

Aplicando la igualdad de Wald a m (t) =E [N (t)]

\(\left\{S_{n} ; n \geq 1\right\}\)Dejen ser las épocas de llegada y\(\left\{X_{n} ; n \geq 1\right\}\) los intervalos entre llegadas para un proceso de renovación. Para cualquier dado\(t>0\), deje\(J\) ser el juicio\(n\) por el que\(S_{n}\) primero rebase\(t\). Tenga en cuenta que\(n\) se especifica por los valores de muestra de\(\left\{X_{1}, \ldots, X_{n}\right\}\) y por lo tanto\(J\) es un ensayo de detención posiblemente defectuoso para\(\left\{X_{n} ; n \geq 1\right\}\).

Ya que\(n\) es el primer juicio para el cual\(S_{n}>t\), vemos que\(S_{n-1} \leq t\) y\(S_{n}>t\). Así\(N(t)\) es\(n-1\) y\(n\) es el valor muestral de\(N(t)+1\). Dado que esto es cierto para todas las secuencias de muestra,\(J=N(t)+1\). Ya que\(N(t)\) es un rv no defectuoso, también\(J\) es, también lo\(J\) es una prueba de detención para\(\left\{X_{n} ; n \geq 1\right\}\).

Entonces podemos emplear la igualdad de Wald para obtener

\[\mathrm{E}\left[S_{N(t)+1}\right]=\bar{X} \mathrm{E}[N(t)+1]=\bar{X}[m(t)+1]\label{4.34} \]

\[m(t)=\frac{\mathrm{E}\left[S_{N(t)+1}\right]}{\bar{X}}-1\label{4.35} \]

Como suele ocurrir con la igualdad de Wald, esto proporciona una relación entre dos cantidades,\(m(t)\) y\(\mathrm{E}\left[S_{N(t)+1}\right]\), que son ambas desconocidas. Esto se utilizará para probar el teorema de renovación elemental por delimitación superior e inferior\(\mathrm{E}\left[S_{N(t)+1}\right]\). El límite inferior es fácil, ya que\(\mathrm{E}\left[S_{N(t)+1}\right] \geq t\), y así\(m(t) \geq t / \bar{X}-1\). De ello se deduce que

\[\frac{m(t)}{t} \geq \frac{1}{\bar{X}}-\frac{1}{t}\label{4.36} \]

Derivamos un límite superior\(\mathrm{E}\left[S_{N(t)+1}\right]\) en la siguiente sección. Primero, sin embargo, como un santity check, considere la Figura 4.12 que ilustra\ ref {4.35} para el caso donde cada uno\(X_{n}\) es un rv determinista donde\(X_{n}=\bar{X}\) con probabilidad 1.

Figura 4.12: Ilustración de\ ref {4.34} para el caso especial donde\(X\) es determinista. Tenga en cuenta que\(m(t)\), en función de\(t\), es entonces la función de escalera ilustrada. En cada incremento de\(t\) por\(\bar{X}\),\(m(t)\) aumenta en uno. Entonces\(m(t)+1\) y\(\mathrm{E}\left[S_{N(t)+1}\right]\) son dos lados de un triángulo rectángulo de pendiente\(1 / \bar{X}\), cediendo (4.34).

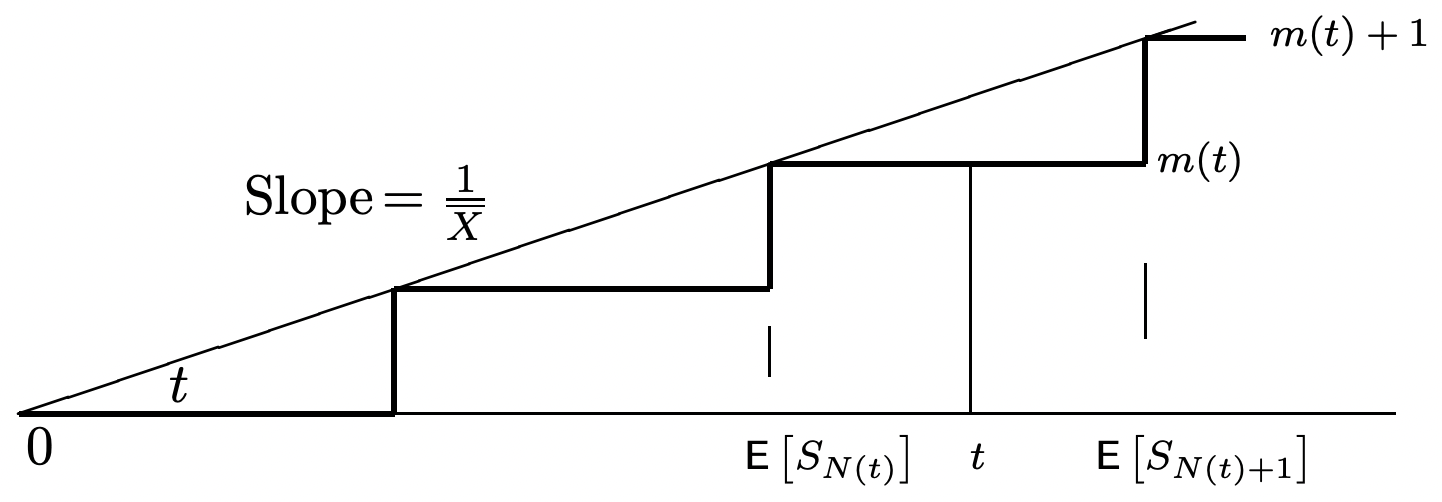
Podría ser desconcertante por qué usamos\(N(t)+1\) más que\(N(t)\) como un juicio de detención para las épocas\(\left\{S_{i} ; i \geq 1\right\}\) en esta aplicación de la igualdad de Wald. Para entender esto, supongamos por ejemplo eso\(N(t)=n\). Cuando un observador ve los valores de muestra de\(S_{1}, \ldots, S_{n}\), con\(S_{n}<t\), el observador normalmente no puede decir (sobre la base de\(S_{1}, \ldots, S_{n}\) solo) si ocurrirá alguna otra llegada en el intervalo\(\left(S_{n}, t\right]\). En otras palabras,\(N(t)=n\) implica eso\(S_{n} \leq t\), pero\(S_{n}<t\) no implica eso\(N(t)=n\). Por otro lado, aun asumiendo\(N(t)=n\), un observador que ve\(S_{1}, \ldots, S_{n+1}\) lo sabe\(N(t)=n\).

Cualquier ensayo de detención (para una secuencia arbitraria de rv\(\left\{S_{n} ; n \geq 1\right\}\)) puede verse como un experimento donde un observador ve valores de muestra\(s_{1}, s_{2}, \ldots\), a su vez hasta que se cumpla la regla de detención. La regla de detención no permite ni mirar hacia adelante ni retroceder para cambiar una decisión anterior. Así la regla: detener en\(N(t)+1\) (para las épocas de renovación\(\left\{S_{n} ; n \geq 1\right\}\)) significa detener en el primer valor de muestra\(\boldsymbol{S}_{i}\) que excede\(t\). No\(s_{n} \leq t\) es necesariamente posible detenerse en el valor final de la muestra sin mirar hacia el siguiente valor de muestra.

Detener pruebas, renovaciones integradas y colas G/G/1

La definición anterior de un juicio de detención es bastante restrictiva ya que se refiere sólo a una sola secuencia de rv. En muchas situaciones de cola, por ejemplo, hay tanto una secuencia de tiempos\(\left\{X_{i} ; i \geq 1\right\}\) de interllegada como una secuencia de tiempos de servicio\(\left\{V_{i} ; i \geq 0\right\}\). Aquí\(X_{i}\) está el intervalo entre llegada entre cliente\(i-1\) y\(i\), donde se supone que un cliente inicial 0 llega a la hora 0, y\(X_{1}\) es la hora de llegada para el cliente 1. El tiempo de servicio del cliente 0 es entonces\(V_{0}\) y cada uno\(V_{i}\),\(i>0\) es el tiempo de servicio del cliente ordinario correspondiente. El número de cliente 0 no es ordinario en el sentido de que llega a la hora fija 0 y no se cuenta en el proceso de conteo de llegadas\(\{N(t) ; t>0\}\).

Ejemplo 4.5.3 (colas G/G/1:).

Considere una cola G/G/1 (el caso de servidor único de la cola G/G/m descrito en el Ejemplo 4.1.2). Asumimos que los clientes son atendidos en orden First-Come-First-Servid (FCFS). ¹² Se supone que tanto los intervalos entre\(\left\{X_{i} ; i \geq 1\right\}\) llegadas como\(\left\{V_{i} ; i \geq 0\right\}\) los tiempos de servicio son IID y se supone que los tiempos de servicio son independientes de los intervalos entre llegadas. La Figura 4.13 ilustra una ruta de muestreo para estas llegadas y salidas.

El Cliente 2 llega a\(s_{2}=x_{1}+x_{2}\). Para el caso que se muestra arriba, esto es antes de que el cliente 1 salga a las\(v_{0}+v_{1}\). Así, la espera del cliente 2 en cola es\(w_{2}^{q}=v_{0}+v_{1}-x_{1}-x_{2}\). Como se ilustra anteriormente, también\(x_{2}+w_{2}^{q}\) es igual al tiempo del sistema del cliente 1, entonces\(w_{2}^{q}=w_{1}^{q}+v_{1}-x_{2}\). El cliente 3 llega cuando el sistema está vacío, por lo que entra en servicio inmediatamente sin esperar en cola, es decir,\(w_{3}^{q}=0\).

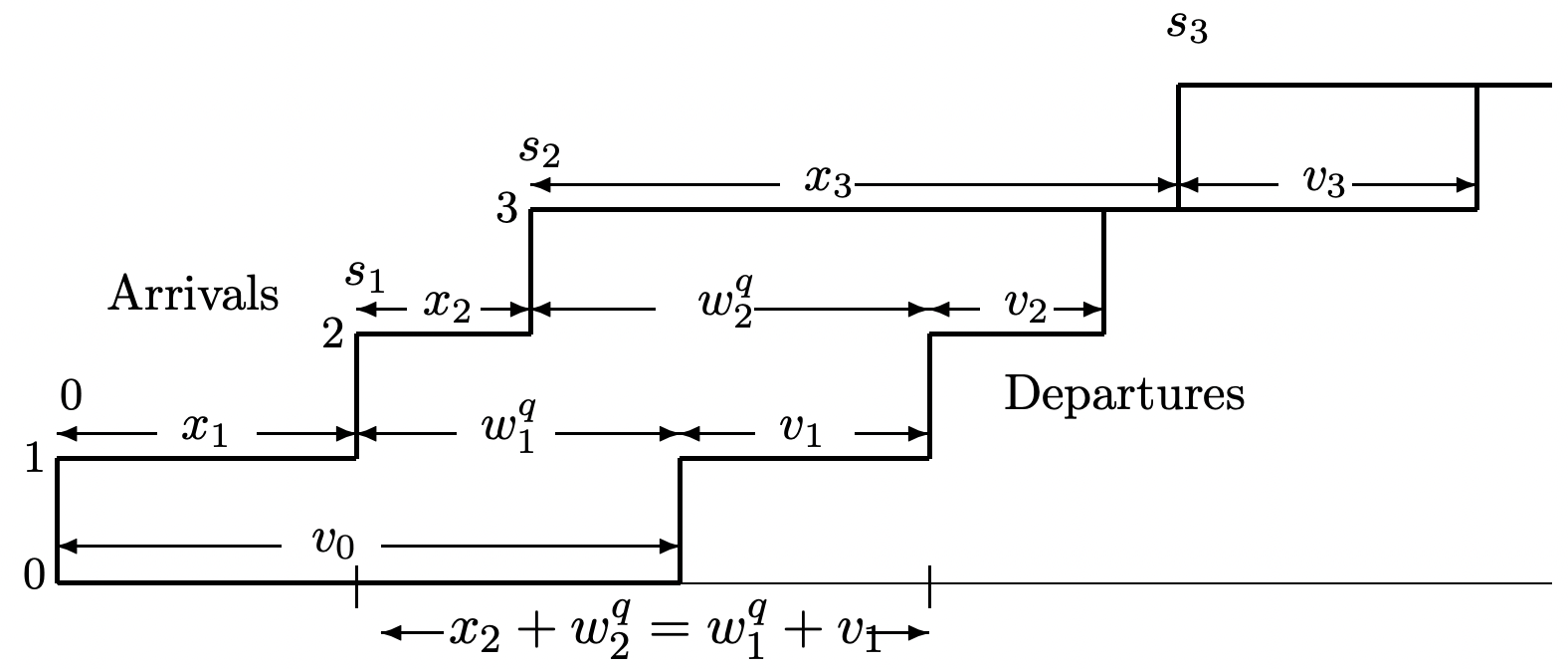
La figura ilustra una ruta de muestra para la cual\(X_{1}<V_{0}\), por lo que el número de llegada 1 espera en cola\(W_{1}^{q}=V_{0}-X_{1}\). Si\(X_{1} \geq V_{0}\), por otro lado, entonces el cliente uno ingresa al servicio de inmediato, es decir, el cliente uno 've un sistema vacío'. En general, entonces W_1^q=\ max\ left (V_ {0} -X_ {1}, 0\ right). De la misma manera, como se ilustra en la figura, si\(W_{1}^{q}>0\), entonces el cliente 2 espera\(W_{1}^{q}+V_{1}-X_{2}\) si es positivo y 0 en caso contrario. Esta misma fórmula funciona si\(W_{1}^{q}=0\), así\(W_{2}^{q}=\max \left(W_{1}^{q}+V_{1}-X_{2}, 0\right)\). En general, se puede ver que

\[W_{i}^{q}=\max \left(W_{i-1}^{q}+V_{i-1}-X_{i}, 0\right)\label{4.37} \]

Esta ecuación se analizará más a fondo en la Sección 7.2 donde nos interesa el retraso en la cola y el retardo del sistema. Aquí nuestros objetivos son más simples, ya que solo queremos mostrar que la subsecuencia de llegadas de clientes\(i\) para las que\(\left\{W_{i}^{q}=0\right\}\) se satisface el evento forman las épocas de renovación de un proceso de renovación. Para ello, primero observe desde\ ref {4.37} (usando inducción si se desea) que\(W_{i}^{q}\) es una función de\(\left(X_{1}, \ldots, X_{i}\right)\) y\(\left(V_{0}, \ldots, V_{i-1}\right)\). Así, si dejamos\(J\) ser los más pequeños\(i>0\) para los cuales\(W_{i}^{q}=0\), entonces\(\mathbb{I}_{J=i}\) es una función de\(\left(X_{1}, \ldots, X_{i}\right)\) y\(\left(V_{0}, \ldots, V_{i-1}\right)\).

Interrumpimos ahora la discusión de las colas G/G/1 con la siguiente generalización de la definición de un juicio de detención.

Definición 4.5.2 (Ensayos de detención generalizada).

Un ensayo de parada generalizada\(J\) para una secuencia de pares de rv\(\left(X_{1}, V_{1}\right),\left(X_{2}, V_{2}\right) \ldots\), es un rv de valor entero positivo tal que, para cada uno\(n \geq 1\), el indicador rv\(\mathbb{I}_{\{J=n\}}\) es una función de\(X_{1}, V_{1}, X_{2}, V_{2}, \ldots, X_{n}, V_{n}\).

La igualdad de Wald puede generalizarse trivialmente para estos juicios generalizados de detención.

Teorema 4.5.2 (Igualdad generalizada de Wald).

Dejar\(\left\{\left(X_{n}, V_{n}\right) ; n \geq 1\right\}\) ser una secuencia de pares de rv, donde cada par es independiente y distribuido idénticamente (IID) a todos los demás pares. Supongamos que cada uno\(X_{i}\) tiene media finita\(\bar{X}\). Si\(J\) es un juicio de detención para\(\left\{\left(X_{n}, V_{n}\right) ; n \geq 1\right\}\) y si\(\mathrm{E}[J]<\infty\), entonces la suma\(S_{J}=X_{1}+X_{2}+\cdots+X_{J}\) satisface

\[\mathrm{E}\left[S_{J}\right]=\bar{X} \mathrm{E}[J]\label{4.38} \]

Prueba

Se omitirá la prueba de ello, ya que es la misma que la prueba del Teorema 4.5.1. De hecho, la definición de detener los ensayos podría generalizarse aún más reemplazando los rv\(V_{i}\) por rv vectoriales o por un número aleatorio de rv, y la igualdad de Wald aún se mantendría. ¹³

Para el ejemplo de la cola G/G/1, tomamos la secuencia de pares a ser\(\left\{\left(X_{1}, V_{0}\right),\left(X_{2}, V_{1}\right), \ldots,\right\}\). Entonces\(\left\{\left(X_{n}, V_{n-1} ; n \geq 1\right\}\right.\) satisface las condiciones del Teorema 4.5.2 (suponiendo que\(\mathrm{E}\left[X_{i}\right]<\infty\). Dejar\(J\) ser la regla de detención generalizada especificando el número de la primera llegada para encontrar una cola vacía. Entonces el teorema relata\(\mathrm{E}\left[S_{J}\right]\), el tiempo esperado\(t>0\) hasta la primera llegada para ver una cola vacía, y\(\mathrm{E}[J]\), el número esperado de llegadas hasta ver una cola vacía.

Aquí es importante, como en muchas aplicaciones, evitar la confusión creada al ver\(J\) como un tiempo de parada. Hemos visto que\(J\) es el número del primer cliente en ver una cola vacía, y\(S_{J}\) es el tiempo hasta que llegue ese cliente.

Existe una posible confusión de tiempo adicional sobre si el tiempo de servicio de un cliente se determina cuando llega el cliente o cuando finaliza el servicio. Esto no hace diferencia, ya que la secuencia ordenada de pares está bien definida y satisface la condición de IID apropiada para usar la igualdad de Wald.

Como suele ocurrir con la igualdad de Wald, no es obvio cómo calcular ninguna cantidad en (4.38), pero es agradable saber que están tan simplemente relacionados. También es interesante ver que, aunque los pares sucesivos\(\left(X_{i}, V_{i}\right)\) se asumen independientes, no es necesario\(V_{i}\) para\(X_{i}\) y ser independientes. Esta falta de independencia no ocurre para la cola G/G/1 (o G/g/M), sino que puede ser útil en situaciones como redes de paquetes donde el tiempo de interllegada entre dos paquetes en un nodo dado puede depender del tiempo de servicio (la longitud) del primer paquete si ambos paquetes provienen del mismo nodo.

Quizás un aspecto más importante de ver la primera renovación para la cola G/G/1 como una prueba de detención es la capacidad de demostrar que las renovaciones sucesivas son de hecho IID. \(X_{2,1}, X_{2,2}, \ldots\)Dejen ser los tiempos entre llegadas siguientes\(J\), la primera llegada para ver una cola vacía. Acondicionamiento encendido\(J=j\), tenemos\(X_{2,1}=X_{j+1}, X_{2,2}=X_{j+2}, \ldots,\). Así\(\left\{X_{2, k} ; k \geq 1\right\}\) es una secuencia IID con la distribución original entre llegadas. Del mismo modo\(\left\{\left(X_{2, k}, V_{2, k}\right) ; k \geq 1\right\}\) es una secuencia de pares IID con la distribución original. Esto es válido para todos los valores\(j\) de muestra del ensayo de detención\(J\). Por lo tanto,\(\left\{\left(X_{2, k}, V_{2, k}\right) ; k \geq 1\right\}\) es estadísticamente independiente de\(J\) y\(\left(X_{i}, V_{i}\right) ; 1 \leq i \leq J\).

El argumento anterior puede repetirse para las llegadas posteriores a un sistema vacío, por lo que hemos demostrado que las llegadas sucesivas a un sistema vacío en realidad forman un proceso de renovación. ¹⁴

Se pueden definir muchas reglas de detención diferentes para las colas, como la primera prueba en la que un número determinado de clientes están en la cola. La igualdad de Wald se puede aplicar a cualquier regla de detención de este tipo, pero se requiere mucho más para que el juicio de detención forme también un punto de renovación. En la primera vez que n clientes están en el sistema, los horarios de salida posteriores dependen en parte de los tiempos de servicio antiguos y en parte de los nuevos tiempos de llegada y servicio, por lo que no existe la independencia requerida para un punto de renovación. Las reglas de detención son útiles para comprender los puntos de renovación incrustados, pero de ninguna manera son equivalentes a los puntos de renovación incrustados.

Por último, nada en el argumento anterior para la cola G/G/1 hizo uso alguno de la disciplina de servicio de la FCFS. Se puede utilizar cualquier disciplina de servicio para la cual la elección de qué cliente servir en un momento dado\(t\) se base únicamente en los tiempos de llegada y servicio de los clientes en el sistema por tiempo\(t\). De hecho, si el servidor nunca está inactivo cuando los clientes están en el sistema, las épocas de renovación no dependerán de la línea de descripción del servicio. También es posible extender estos argumentos a la cola G/g/m, aunque la disciplina de servicio puede afectar los puntos de renovación en este caso.

Teorema de Little

El teorema de Little es un resultado importante de colas que indica que el número esperado de clientes en un sistema de colas es igual al producto de la tasa de llegada y el tiempo esperado que cada cliente espera en el sistema. Este resultado es cierto bajo condiciones muy generales; utilizamos la cola G/G/1 con el servicio FCFS como ejemplo específico, pero la razón de la mayor generalidad será clara a medida que avancemos. Obsérvese que el teorema no nos dice cómo encontrar ni el número esperado ni la espera esperada; solo dice que si se puede encontrar uno, el otro también se puede encontrar.

La figura también muestra los valores de muestra\(s_{1}^{r}\) y\(s_{2}^{r}\) de las dos primeras llegadas que ven un sistema vacío (recuerde de la Sección 4.5.3 que la subsecuencia de llegadas que ven un sistema vacío forma un proceso de renovación).

La Figura 4.14 ilustra una ruta de muestra para una cola G/G/1 con servicio FCFS. Ilustra una ruta de muestra\(a(t)\) para el proceso de llegada\(A(t)=N(t)+1\), es decir, el número de llegadas de clientes\([0, t]\), específicamente incluyendo el número de cliente 0 que llega a\(t=0\). De igual manera, ilustra el proceso de salida\(D(t)\), que es el número de salidas hasta el tiempo\(t\), nuevamente incluyendo al cliente 0. La diferencia,\(L(t)=A(t)-D(t)\), es entonces el número en el sistema en el momento\(t\).

Recordemos de la Sección 4.5.3 que la subsecuencia de llegadas de clientes para\(t>0\) que vean un sistema vacío forman un proceso de renovación. En realidad, mostramos un poco más que eso. No solo los intervalos entre renovaciones,\(X_{i}^{r}=S_{i}^{r}-S_{i-1}^{r}\) IID, sino que el número de llegadas de clientes en cada intervalo entre renovaciones son IID, y los intervalos entre llegadas y los tiempos de servicio entre intervalos entre renovaciones son IID. En la figura se muestran los valores muestrales\(s_{1}^{r}\) y\(s_{2}^{r}\) de las dos primeras épocas de renovación.

La esencia del teorema de Little se puede ver observando que\(\int_{0}^{S_{1}^{r}} L(\tau) d \tau\) en la figura se encuentra el área entre las funciones de paso superior e inferior, integrada a la primera vez que las dos funciones de paso se vuelven iguales (es decir, el sistema se vuelve vacío). Para el valor de muestra en la figura, esta integral es igual a\(w_{0}+w_{1}+w_{2}\). En cuanto a los rv,

\[\int_{0}^{S_{1}^{r}} L(\tau) d \tau=\sum_{i=0}^{N\left(S_{1}^{r}\right)-1} W_{i}\label{4.39} \]

La misma relación existe en cada intervalo entre renovaciones, y en particular podemos definir\(L_{n}\) para cada uno\(n \geq 1\) como

\[L_{n}=\int_{S_{n-1}^{r}}^{S_{n}^{r}} L(\tau) d \tau=\sum_{i=N\left(S_{n-1}^{r}\right)}^{N\left(S_{n}^{r}\right)-1} W_{i}\label{4.40} \]

La interpretación de esto es mucho más sencilla que la notación. La función de paso de llegada y la función de paso de salida en la Figura 4.14 se separan cada vez que hay clientes en el sistema (el sistema está ocupado) y son iguales cuando el sistema está vacío. Las renovaciones ocurren cuando el sistema pasa de vacío a ocupado, por lo que la\(n\) renovación es al comienzo\(n\) del período ocupado. Entonces\(L_{n}\) es el área de la región entre las funciones de dos pasos durante\(n\) el período ocupado. Por geometría simple, esta área es también la suma de los tiempos de espera del cliente durante ese período ocupado. Finalmente, dado que los intervalos entre llegadas y los tiempos de servicio en cada periodo ocupado son IID con respecto a aquellos en cada otro periodo ocupado\(L_{1}, L_{2}, \ldots\), la secuencia, es una secuencia de IID rv.

La función\(L(\tau)\) tiene el mismo comportamiento que una función de recompensa de renovación, pero es un poco más general, siendo una función de más de la edad y duración del proceso de conteo de renovación\(\left\{N^{r}(t) ; t>0\right\}\) en\(t=\tau\). Sin embargo, el hecho de que\(\left\{L_{n} ; n \geq 1\right\}\) sea una secuencia IID nos permite utilizar la misma metodología para tratar\(L(\tau)\) como se utilizó anteriormente para tratar las funciones de renovación-recompensa. Ahora declaramos y probamos el teorema de Little. La prueba es casi la misma que la del Teorema 4.4.1, por lo que no vamos a detenernos en ella.

Teorema 4.5.3 (Poco).

Para una cola FCFS G/G/1 en la que el intervalo entre renovaciones esperado es finito, el número medio de tiempo límite de clientes en el sistema es igual, con probabilidad 1, a una constante denotada como\(\overline{L}\). El tiempo de espera promedio de ruta de muestra por cliente también es igual, con probabilidad 1, a una constante denotada como\(\overline{W}\). Finalmente,\(\overline{L}=\lambda \overline{W}\) dónde\(\lambda\) está la tasa de llegada del cliente, es decir, la recíproca del tiempo interllegada esperado.

Prueba

Tenga en cuenta que para cualquiera\(t>0\), se\(\int_{0}^{t}(L(\tau) d \tau\) puede expresar como la suma sobre los períodos ocupados completados antes\(t\) más un término residual que involucra el período ocupado incluyendo\(t\). El término residual puede estar delimitado por la parte superior por la integral durante ese período completo ocupado. Usando esto con (4.40), tenemos

\[\sum_{n=1}^{N^{r}(t)} \mathrm{L}_{n} \leq \int_{\tau=0}^{t} L(\tau) d \tau \leq \sum_{i=0}^{N(t)} W_{i} \leq \sum_{n=1}^{N^{r}(t)+1} \mathrm{~L}_{n}\label{4.41} \]

Suponiendo que el intervalo entre renovaciones esperado\(\mathrm{E}\left[X^{r}\right]\),, es finito, podemos dividir ambos lados de\ ref {4.41} por\(t\) e ir al límite\(t \rightarrow \infty\). Del mismo argumento que en el Teorema 4.4.1,

\[\lim _{t \rightarrow \infty} \frac{\sum_{i=0}^{N(t)} W_{i}}{t}=\lim _{t \rightarrow \infty} \frac{\int_{\tau=0}^{t} L(\tau) d \tau}{t}=\frac{\mathrm{E}\left[\mathrm{L}_{n}\right]}{\mathrm{E}\left[X^{r}\right]} \quad \text { with probability } 1\label{4.42} \]

La igualdad de la derecha muestra que el promedio de tiempo limitante de\(L(\tau)\) existe con probabilidad 1 y es igual a\(\overline{L}=\mathrm{E}\left[L_{n}\right] / \mathrm{E}\left[X^{r}\right]\). La cantidad a la izquierda de\ ref {4.42} ahora se puede dividir como tiempo de espera por cliente multiplicado por el número de clientes por unidad de tiempo, es decir,

\[\lim _{t \rightarrow \infty} \frac{\sum_{i=0}^{N(t)} W_{i}}{t}=\lim _{t \rightarrow \infty} \frac{\sum_{i=0}^{N(t)} W_{i}}{N(t)} \lim _{t \rightarrow \infty} \frac{N(t)}{t}\label{4.43} \]

De (4.42), el límite en el lado izquierdo de\ ref {4.43} existe (y es igual a\(\overline{L}\)) con probabilidad 1. El segundo límite a la derecha también existe con probabilidad 1 por la ley fuerte para los procesos de renovación, aplicada a\(\{N(t) ; t>0\}\). Este límite se denomina tasa de llegada\(\lambda\), y es igual al recíproco del intervalo medio entre llegadas para\(\{N(t)\}\). Dado que estos dos límites existen con probabilidad 1, el primer límite a la derecha, que es el tiempo de espera promedio de ruta de muestra por cliente, denotado\(\overline{W}\), también existe con probabilidad 1.

Al revisar esta prueba y el desarrollo de la cola G/G/1 antes del teorema, vemos que hubo una idea simple, expresada por (4.39), combinada con mucha complejidad notacional debido a que estábamos tratando tanto con un proceso de conteo de llegadas como con un proceso\(\{N(t) ; t>0\}\) de conteo de renovación incrustado \(\left\{N^{r}(t) ; t>0\right\}\). Lo difícil, matemáticamente, fue mostrar que en realidad\(\left\{N^{r}(t) ; t>0\right\}\) es un proceso de renovación y mostrar que los\(L_{n}\) son IID, y aquí era donde necesitábamos entender las reglas de detención.

Recordemos que asumimos antes que los clientes partieron de la cola en el mismo orden en el que llegaron. De la Figura 4.15, sin embargo, es claro que no se requiere orden FCFS para el argumento. Así el teorema se generaliza a sistemas con múltiples servidores y disciplinas de servicio arbitrarias en las que los clientes no siguen el orden FCFS. De hecho, todo lo que el argumento requiere es que el sistema tenga renovaciones (que son IID por definición de renovación) y que el intervalo entre renovaciones sea finito con probabilidad 1.

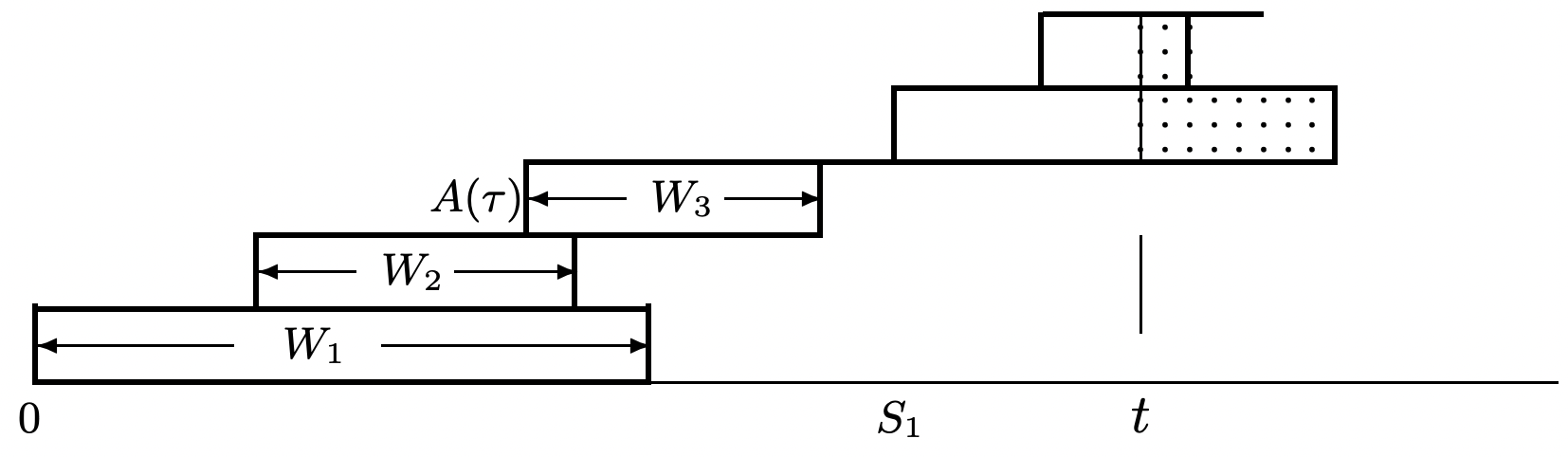Figura 4.15: Llegadas y salidas en sistemas no FCFS. El servidor, por ejemplo, podría funcionar simultáneamente (a una tarifa reducida) en todos los clientes del sistema, y así completar el servicio para clientes con pequeñas necesidades de servicio antes de completar llegadas antes con mayores necesidades de servicio. Tenga en cuenta que el borde derecho dentado del diagrama no representa el número de desaparaturas, pero esto no es esencial para el argumento.

Por ejemplo, si se da mayor prioridad a los clientes con tiempos de servicio pequeños, entonces no es difícil ver que se disminuirá el número promedio de clientes en el sistema y el tiempo de espera promedio por cliente. Sin embargo, si el servidor siempre está ocupado cuando hay trabajo por hacer, se puede ver que los tiempos de renovación no se ven afectados. Los discipinos de servicio se discutirán más a fondo en la Sección 5.6.

El mismo argumento que en el teorema de Little se puede utilizar para relacionar el número promedio de clientes en una sola cola de servidor (sin contar el servicio) con la espera promedio en la cola (sin contar el servicio). Las renovaciones aún ocurren en las llegadas a un sistema vacío, y la integral de los clientes en cola durante un período ocupado sigue siendo igual a la suma de los tiempos de espera de la cola. Dejar\(L^{q}(t)\) ser el número en la cola en el momento\(t\) y dejar\(\bar{L}^{q}=\lim _{t \rightarrow \infty}(1 / t) \int_{0}^{t} L^{q}(\tau) d \tau\) ser la espera de cola promedio de tiempo. Dejando\(\overline{W}^{q}\) ser el tiempo de espera promedio de ruta de muestra en cola,

\[\overline{L}^{q}=\lambda \overline{W}^{q} \label{4.44} \]

El mismo argumento también se puede aplicar a la instalación de servicio de una sola cola de servidor. El promedio de tiempo del número de clientes en el servidor es solo la fracción de tiempo que el servidor está ocupado. Denotando esta fracción por\(\rho\) y el tiempo de servicio esperado por\(\overline{V}\), obtenemos

\[\rho=\lambda \overline{V}\label{4.45} \]

Tiempo de cola esperado para una cola M/G/1

Para nuestro último ejemplo del uso de procesos de renovación-recompensa, consideramos el tiempo de cola esperado en una cola M/G/1. De nuevo asumimos que una llegada a un sistema vacío ocurre en el tiempo 0 y las renovaciones ocurren en las llegadas posteriores a un sistema vacío. En cualquier momento dado\(t\), deje\(L^{q}(t)\) ser el número de clientes en la cola (sin contar al cliente en servicio, si los hay) y dejar que\(R(t)\) sea la vida residual del cliente en servicio. Si ningún cliente está en servicio,\(R(t)=0\), y de lo contrario\(R(t)\) es el tiempo restante hasta que se complete el servicio actual. Deje\(U(t)\) ser el tiempo de espera en cola que sería experimentado por un cliente que llega a tiempo\(t\). Esto a menudo se llama el trabajo inacabado en la literatura de colas y representa el retraso hasta que todos los clientes actualmente en el sistema completen el servicio. Así el rv\(U(t)\) es igual a\(R(t)\), la vida residual del cliente en servicio, más los tiempos de servicio de cada uno de los\(L^{q}(t)\) clientes que actualmente esperan en la cola.

\[U(t)=\sum_{i=1}^{L^{q}(t)} V_{N(t)-i}+R(t),\label{4.46} \]

donde\(N(t)-i\) está el número de cliente del\(i\) th cliente en la cola en el momento\(t\). Dado que\(L^{q}(t)\) es una función solo de los tiempos de interllegada\((0, t)\) y los tiempos de servicio de los clientes que ya han sido atendidos, vemos que para cada valor de muestra\(L^{q}(t)=\ell\), los rv tienen\(\widetilde{V}_{1}, \ldots, \widetilde{V}_{\ell}\) cada uno la distribución del tiempo de servicio\(\mathrm{F}_{V}\). Así, tomando los valores esperados,

\[\mathrm{E}[U(t)]=\mathrm{E}\left[L^{q}(t)\right] \mathrm{E}[V]+\mathrm{E}[R(t)].\label{4.47} \]

La Figura 4.16 ilustra cómo encontrar el promedio de tiempo de\(R(t)\). Viendo\(R(t)\) como recompensa

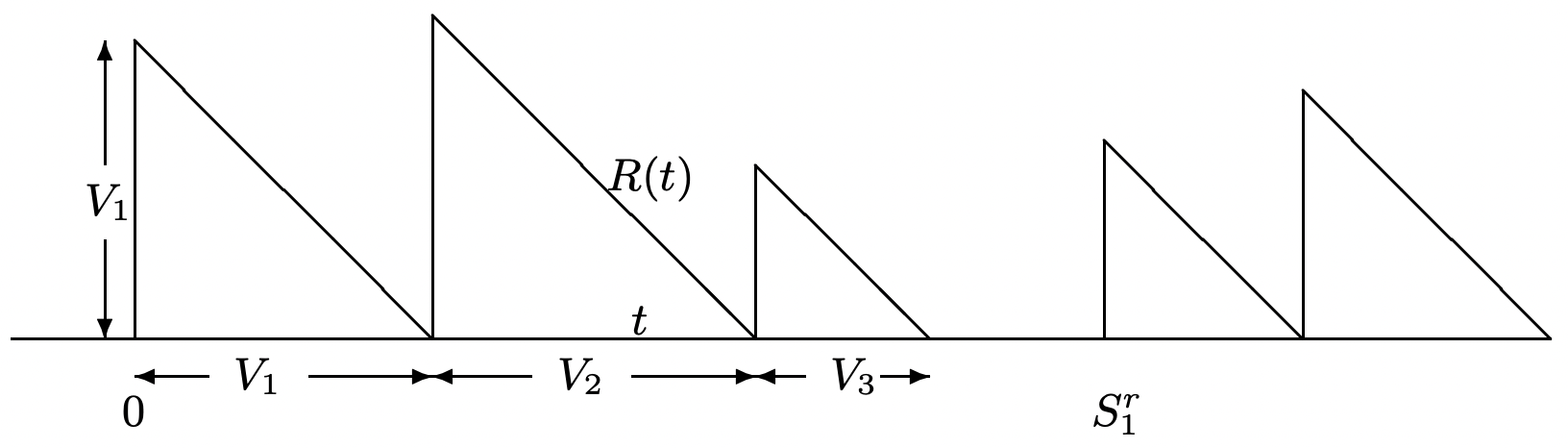Figura 4.16: Valor muestral de la función de vida residual de los clientes en servicio.

, podemos encontrar la recompensa acumulada hasta el tiempo t como la suma de áreas triangulares.

Primero, considere\(\int R(\tau) d \tau\) de 0 a\(S_{N^{r}(t)}^{r}\), es decir, la recompensa acumulada hasta la época de renovación final en\([o, t] t\). Tenga en cuenta que no sólo\(S_{N^{r}(t)}^{r}\) es una época de renovación para el proceso de renovación, sino también una época de llegada para el proceso de llegada; en particular, es la época de\(N\left(S_{N^{r}(t)}^{r}\right) \text { th }\) llegada, y las llegadas\(N\left(S_{N^{r}(t)}^{r}\right)-1\) más tempranas son los clientes que han recibido servicio hasta el momento\(S_{N^{r}(t)}^{r}\). Por lo tanto,

\(\int_{0}^{S_{N^{r}(t)}^{r}} R(\tau) d \tau=\sum_{i=0}^{N\left(S_{N^{r}(t)}^{r}\right)-1} \frac{V_{i}^{2}}{2} \leq \sum_{i=0}^{N(t)} \frac{V_{i}^{2}}{2}.\)

De manera similar podemos encuadrar superior el término a la derecha arriba por\(\int_{0}^{S_{N^{r}(t)+1}^{r}} R(\tau) d \tau\). También sabemos (de pasar por prácticamente el mismo argumento varias veces) que\((1 / t) \int_{\tau=0}^{t} R(\tau) d \tau\) se acercará a un límite ¹⁵ con probabilidad 1 as\(t \rightarrow \infty\), y que el límite quedará sin cambios si\(t\) se sustituye por\(S_{N^{r}(t)}^{r}\) o\(S_{N^{r}(t)+1}^{r}\). Así, tomando\(\lambda\) como tasa de llegada,

\(\lim _{t \rightarrow \infty} \frac{\int_{0}^{t} R(\tau) d \tau}{t}=\lim _{t \rightarrow \infty} \frac{\sum_{i=1}^{A(t)} V_{i}^{2}}{2 A(t)} \frac{A(t)}{t}=\frac{\lambda \mathrm{E}\left[V^{2}\right]}{2}\quad\text{WP1}\)

Veremos en la siguiente sección que el promedio de tiempo anterior puede ser reemplazado por un ensemble-promedio limitante, de manera que

\[\lim _{t \rightarrow \infty} \mathrm{E}[R(t)]=\frac{\lambda \mathrm{E}\left[V^{2}\right]}{2}.\label{4.48} \]

El siguiente apartado también muestra que existe una forma limitante ensemble-promedio de (4.44), lo que demuestra que\(\lim _{t \rightarrow \infty} \mathrm{E}\left[L^{q}(t)\right]=\lambda \overline{W}^{q}\). Sustituyendo este plus\ ref {4.48} en (4.47), obtenemos

\[\lim _{t \rightarrow \infty} \mathrm{E}[U(t)]=\lambda \mathrm{E}[V] \overline{W}^{q}+\frac{\lambda \mathrm{E}\left[V^{2}\right]}{2}.\label{4.49} \]

Así\(\mathrm{E}[U(t)]\) es asintóticamente independiente de\(t\). Ahora es importante distinguir entre\(\mathrm{E}[U(t)]\) y\(\overline{W}^{q}\). El primero es el trabajo inacabado esperado en el momento\(t\), que es el retraso en la cola en el que incurriría un cliente al llegar\(t\); el segundo es el retraso de cola esperado promedio de ruta de muestra. Para las llegadas a Poisson, la probabilidad de una llegada\((t, t+\delta]\) es independiente de todas las llegadas anteriores y los horarios de servicio, por lo que es independiente de\(U(t)\) ¹⁶. Así, en el límite\(t \rightarrow \infty\), cada llegada enfrenta un retraso esperado\(\lim _{t \rightarrow \infty} \mathrm{E}[U(t)]\), por lo que\(\lim _{t \rightarrow \infty} \mathrm{E}[U(t)]\) debe ser igual a\(\overline{W}^{q}\). Sustituyendo esto en (4.49), obtenemos la célebre fórmula PollacZekkhinchin,

\[\overline{W}^{q}=\frac{\lambda \mathrm{E}\left[V^{2}\right]}{2(1-\lambda \mathrm{E}[V])}.\label{4.50} \]

Este retraso de cola tiene algunas de las características peculiares de la vida residual, y en particular, si\(\mathrm{E}\left[V^{2}\right]=\infty\), el retraso de cola esperado limitante es infinito incluso cuando el tiempo de servicio esperado es menor que el intervalo esperado entre llegadas.

Al tratar de visualizar por qué el retraso en la cola es tan grande cuando\(\mathrm{E}\left[V^{2}\right]\) es grande, tenga en cuenta que mientras se está llevando a cabo un servicio particularmente largo, numerosas llegadas están llegando al sistema, y todas están siendo retrasadas por este único servicio largo. Es decir, el número de nuevos clientes retenidos por un servicio largo es proporcional a la duración del servicio, y la cantidad que cada uno de ellos es retenido también es proporcional a la duración del servicio. Esta visualización es bastante cruda, pero sí sirve para explicar el segundo momento de\(V\) in (4.50). A este fenómeno se le llama a veces el “efecto camión lento” debido a la acumulación de autos detrás de un camión lento en una carretera de un solo carril.

Para una cola G/G/1,\ ref {4.49} sigue siendo válida, pero los tiempos de llegada ya no son independientes de\(U(t)\), por lo que normalmente\(\mathrm{E}[U(t)] \neq \overline{W}^{q}\). Como ejemplo, supongamos que el tiempo de servicio se distribuye uniformemente entre\(1-\epsilon\) y\(1+\epsilon\) y que el intervalo entre llegadas se distribuye uniformemente entre\(2-\epsilon\) y\(2+\epsilon\). Suponiendo que\(\epsilon<1 / 2\), el sistema no tiene colas y\(\overline{W}^{q}=0\). Por otro lado, para pequeños\(\epsilon\),\(\lim _{t \rightarrow \infty} \mathrm{E}[U(t)] \sim 1 / 4\) (es decir, el servidor está ocupado la mitad del tiempo con trabajos inconclusos que van de 0 a 1).

---

⁸ Por ejemplo, los jugadores de poker no toman amablemente a un jugador que intenta retirar su apuesta cuando alguien más gana la mano. De igual manera, un estadístico que recoja datos sobre fallas de productos no debe responder a una falla para luego registrar un ensayo anterior como tiempo de detención, no registrando así el fallo.

⁹ Los ensayos de detención se denominan con mayor frecuencia tiempos de detención o tiempos de parada opcionales en la literatura. Sin embargo, en nuestra primera aplicación importante de un juicio de detención, el juicio de detención es el primer juicio\(n\) en el que una época de renovación\(S_{n}\) excede un tiempo determinado\(t\). Ver este juicio como un tiempo genera considerable confusión.

¹⁰ Esto puede resultar bastante confuso inicialmente, ya que (como se ve en el ejemplo de la Figura 4.11) no\(X_{n}\) es necesariamente independiente del suceso\(\{J=n\}\)\(\{J=n+1\}\), ni de, etc. En otras palabras, dado que la detención no ha ocurrido antes del juicio\(n\), entonces\(X_{n}\) puede tener mucho que ver con el juicio en el que se produce la detención. No obstante, como se mostró anteriormente, no\(X_{n}\) tiene nada que ver con si\(\{J<n\}\) o\(\{J \geq n\}\).

¹¹ Esto se mostrará cuando veamos este ejemplo como una cadena de Markov de nacimiento y muerte en el Capítulo 5.

¹² Para las colas de un solo servidor, esto a veces se conoce como servicio First-In-First-Out (FIFO).

¹³ De hecho, a veces\(J\) se define como una regla de detención si\(\mathbb{I}_{\{J \geq n\}}\) es independiente de\(X_{n}, X_{n+1}, \ldots\) para cada uno\(n\). Esto hace que sea fácil probar la igualdad de Wald, pero bastante difícil de ver cuándo se mantiene la definición\(\mathbb{I}_{\{J=n\}}\), especialmente porque, por ejemplo, suele depender de\(X_{n}\) (ver nota 7).

¹⁴ Confesión por autor: Desde hace unos 15 años, creí erróneamente que era obvio que las llegadas a un sistema vacío en una cola de G/g/m forman un proceso de renovación. Por lo tanto, no puedo esperar que los lectores se entusiasmen con la prueba anterior. Sin embargo, es un buen ejemplo de cómo usar los tiempos de parada para ver claramente los puntos que de otro modo serían turbios.

¹⁵ De hecho, uno podría simplemente tomar el límite sin traer el proceso de renovación, ya que ya está claro que el proceso de renovación justifica el límite con probabilidad 1.

¹⁶ A esto se le suele llamar la propiedad PASTA, lo que significa llegadas a Poisson ver promedios de tiempo. Esto se sostiene con gran generalidad, requiriendo sólo que existan medias de tiempo y que los parámetros de interés en un momento dado\(t\) sean independientes de las futuras llegadas. Al mismo tiempo, esta propiedad es algo vaga, por lo que debe ser utilizada para ayudar a la intuición más que para probar teoremas.