4.10: Ejercicios

Ejercicio 4.1

El propósito de este ejercicio es mostrar que para un proceso de renovación arbitrario,\(N(t)\), el número de renovaciones en\((0, t]\) es una variable aleatoria (no defectuosa).

1. Dejar\(X_{1}, X_{2}, \ldots\), ser una secuencia de IID rv inter-renovaciones. dejar que\(S_{n}=X_{1}+\cdots+X_{n}\) sean las épocas de renovación correspondientes para cada uno\(n \geq 1\). Supongamos que cada uno\(X_{i}\) tiene una expectativa finita\(\overline{X}>0\) y, por lo que se da\(t > 0\), utilizar la débil ley de los grandes números para demostrarlo\(\lim _{n \rightarrow \infty} \operatorname{Pr}\left\{S_{n} \leq t\right\}=0\).
2. Use la parte a) para mostrar eso\(\lim _{n \rightarrow \infty} \operatorname{Pr}\{N \geq n\}=0\) y explicar por qué esto significa que\(N(t)\) es un rv, es decir, no es defectuoso.
3. Ahora supongamos que los\(X_{i}\) no tienen una media finita. Considera truncar cada uno\(X_{i}\) a\(\breve{X}_{i}\), donde para cualquier dado\(b>0\),\(\breve{X}_{i}=\min \left(X_{i}, b\right)\). \(\breve{N}(t)\)Sea el proceso de conteo de renovación para los intervalos entre renovaciones\(\breve{X}_{i}\). Demostrar que no\(\breve{N}(t)\) es defectuoso para cada uno\(t > 0\). Demostrar eso\(N(t) \leq \breve{N}(t)\) y así eso no\(N(t)\) es defectuoso. Nota: Los intervalos grandes entre renovaciones crean pequeños valores de\(N(t)\), y por lo tanto no\(\mathrm{E}[X]=\infty\) tiene nada que ver con valores potencialmente grandes de\(N(t)\), por lo que el argumento aquí fue puramente técnico.

Ejercicio 4.2

El propósito de este ejercicio es mostrar que, para un proceso de renovación arbitrario,\(N(t)\), el número de renovaciones en\((0, t]\), tiene una expectativa finita.

1. Que los intervalos entre renovaciones tengan la distribución\(\mathrm{F}_{X}(x)\), con, como de costumbre,\(\mathrm{F}_{X}(0)=0\). Usar cualquier combinación de matemáticas y sentido común es cómodo para ti, demuestra que los números\(\epsilon>0\) y\(\delta>0\) deben existir de tal manera que\(\mathrm{F}_{X}(\delta) \leq 1-\epsilon\). En otras palabras, debes demostrar que un rv positivo debe tomar algún rango de valores delimitados lejos de cero con probabilidad positiva.
2. \(\operatorname{Pr}\left\{S_{n} \leq \delta\right\} \leq(1-\epsilon)^{n}\)Demuéstralo.
3. \(\mathrm{E}[N(\delta)] \leq 1 / \epsilon\)Demuéstralo.
4. Demostrar eso por cada entero\(k\),\(\mathrm{E}[N(k \delta)] \leq k / \epsilon\) y así eso\(\mathrm{E}[N(t)] \leq \frac{t+\delta}{\epsilon \delta}\) para cualquier\(t > 0\).
5. Usa tu resultado aquí para demostrar que no\(N(t)\) es defectuoso.

Ejercicio 4.3

Dejen\(\left\{X_{i} ; i \geq 1\right\}\) ser los intervalos inter-renovacion de un proceso de renovacion generalizados para permitir intervalos inter-renovacion de tamaño 0 y let\(\operatorname{Pr}\left\{X_{i}=0\right\}=\alpha\),\(0<\alpha<1\). Let\(\left\{Y_{i} ; i \geq 1\right\}\) Ser la secuencia de intervalos entre llegadas distintos de cero. Por ejemplo, si\(X_1=x_{1}>0, X_{2}=0, X_{3}=x_{3}>0, \ldots\), entonces\(Y_{1}=x_{1}, Y_{2}=x_{3}, \ldots,.\)

1. Encuentra la función de distribución de cada uno\(Y_{i}\) en términos de la de la\(X_{i}\).
2. Encuentra el PMF del número de llegadas del proceso de renovación generalizada en cada época en la que ocurren las llegadas.
3. Explicar cómo ver el proceso de renovación generalizada como un proceso de renovación ordinario con intervalos entre renovaciones\(\left\{Y_{i} ; i \geq 1\right\}\) y llegadas a granel en cada época de renovación.
4. Cuando un proceso de renovación generalizada es visto como un proceso ordinario de renovación con llegadas a granel, ¿cuál es la distribución de las llegadas de graneles? (El objetivo de esta parte es ilustrar que las llegadas a granel en un proceso ordinario de renovación son considerablemente más generales que los procesos de renovación generalizados).

Ejercicio 4.4

¿Es cierto para un proceso de renovación que:

1. \(N(t)<n\)si y solo si\(S_{n}>t\)?
2. \(N(t) \leq n\)si y solo si\(S_{n} \geq t\)?
3. \(N(t)>n\)si y solo si\(S_{n}<t\)?

Ejercicio 4.5

(Esto demuestra que la convergencia WP1 implica convergencia en probabilidad.) Dejar\(\left\{Y_{n} ; n \geq 1\right\}\) ser una secuencia de rv que converja a 0 WP1. Para cualquier número entero positivo\(m\) y\(k\), let

\(A(m, k)=\left\{\omega:\left|Y_{n}(\omega)\right| \leq 1 / k \quad \text { for all } n \geq m\right\}\)

1. Mostrar que si\(\lim _{n \rightarrow \infty} Y_{n}(\omega)=0\) para algunos dado\(\omega\), entonces (para cualquier dado\(k\))\(\omega \in A(m, k)\) para algún entero positivo\(m\).
2. Demostrar que para todos\(k \geq 1\)

   \(\operatorname{Pr}\left\{\bigcup_{m=1}^{\infty} A(m, k)\right\}=1\)

3. Demuéstralo, para todos\(m \geq 1\),\(A(m, k) \subseteq A(m+1, k)\). Usa esto (más (1.9)) para mostrar que

   \(\lim _{m \rightarrow \infty} \operatorname{Pr}\{A(m, k)\}=1\)

4. Demuéstralo si\(\omega \in A(m, k)\), entonces\(\left|Y_{m}(\omega)\right| \leq 1 / k\). Usa esto (más la parte c) para mostrar que

   \(\lim _{m \rightarrow \infty} \operatorname{Pr}\left\{\left|Y_{m}\right|>1 / k\right\}=0\)

Ya que\(k \geq 1\) es arbitrario, esto demuestra que\(\left\{Y_{n} ; n \geq 1\right\}\) converge en la probabilidad.

Ejercicio 4.6

En este ejercicio, encontramos una expresión explícita para\(\left\{\omega: \lim _{n} Y_{n}=0\right\}\). Puedes usar cualquier nivel de precisión matemática con el que te sientas cómodo.

1. \(\left\{Y_{n} ; n \geq 1\right\}\)Sea una secuencia de rv. Usando la definición de convergencia para una secuencia de números, justifique las siguientes equivalencias establecidas:

   \ (\ begin {aligned}
   \ left\ {\ omega:\ lim _ {n} Y_ {n} (\ omega) =0\ right\} &=\ bigcap_ {k=1} ^ {\ infty}\ left\ {\ omega:\ text {existe un} m\ text {tal que}\ izquierda|y_ {n} (\ omega)\ derecha|\ leq 1 k/\ texto {para todos} n\ geq m\ derecho\}\\
   &=\ bigcap_ {k=1} ^ {\ infty}\ bigcup_ {m=1} ^ {\ infty}\ izquierda\ {\ omega: Y_ {n} (\ omega)\ leq 1/k\ texto {para todos} n\ geq m\ derecha\}\\
   &=\ bigcap_ {k=1} ^ {\ infty}\ bigcup_ {m=1} ^ {\ infty}\ bigcap_ {n=m} ^ {\ infty}\ izquierda\ {omega: Y_ {n} (\ omega)\ leq 1/k\ derecha\}
   \ final {alineado}\)

2. Explique cómo esto demuestra que\(\left\{\omega: \lim _{n} Y_{n}(\omega)=0\right\}\) debe ser un evento.
3. Utilice las leyes de DeMorgan para demostrar que el complemento de la equivalencia anterior es

   \(\left\{\omega: \lim _{n} Y_{n}(\omega)=0\right\}^{c}=\bigcup_{k=1}^{\infty} \bigcap_{m=1}^{\infty} \bigcup_{n=m}^{\infty}\left\{\omega: Y_{n}(\omega)>1 / k\right\}\)

4. \(\left\{Y_{n} ; n \geq 1\right\}\)Demostrar que para converger WP1, es necesario y suficiente para satisfacer

   \(\operatorname{Pr}\left\{\bigcap_{m=1}^{\infty} \bigcup_{n=m}^{\infty}\left\{Y_{n}>1 / k\right\}\right\}=0 \quad \text { for all } k \geq 1\)

5. \(\left\{Y_{n} ; n \geq 1\right\}\)Demostrar que para converger WP1, es necesario y suficiente para satisfacer

   \(\lim _{m \rightarrow \infty} \operatorname{Pr}\left\{\bigcup_{n=m}^{\infty}\left\{Y_{n}>1 / k\right\}\right\}=0 \quad \text { for all } k \geq 1\)

Pista: Utilice la parte a) del Ejercicio 4.7. Nota: La Parte e) proporciona una condición equivalente que a menudo es útil para establecer la convergencia WP1. También pone de manifiesto con bastante claridad la diferencia entre convergencia WP1 y convergencia en probabilidad.

Ejercicio 4.7

Considerar el suceso\(\bigcap_{m \geq 1} \bigcup_{n \geq m} A_{n}\) donde\(A_{1}, A_{2}, \ldots\), son hechos arbitrarios.

1. Demostrar que

   \(\lim _{m \rightarrow \infty} \operatorname{Pr}\left\{\bigcup_{n \geq m} A_{n}\right\}=0 \quad \Longleftrightarrow \quad \operatorname{Pr}\left\{\bigcap_{m \geq 1} \bigcup_{n \geq m} A_{n}\right\}=0\)

   Pista: Aplicar el complemento de (1.9).

2. Demuéstralo si\(\sum_{m=1}^{\infty} \operatorname{Pr}\left\{A_{m}\right\}<\infty\), entonces\(\operatorname{Pr}\left\{\bigcap_{m} \bigcup_{n \geq m} A_{n}\right\}=0\). Pista: Recordemos que si\(\sum_{m=1}^{\infty} \operatorname{Pr}\left\{A_{m}\right\}<\infty\), entonces\(\lim _{m \rightarrow \infty} \operatorname{Pr}\left\{\bigcup_{n \geq m} A_{n}\right\}=0\). Combine esto con a). Este conocido resultado se llama el lema Borel-Cantelli.
3. El conjunto a menudo\(\operatorname{Pr}\left\{\bigcap_{m} \bigcup_{n \geq m} A_{n}\right\}\) se conoce como el conjunto de ω que están contenidos en infinitamente muchos de los\(A_{n}\). Sin tratar de ser precisos sobre lo que significa esta última afirmación, explique por qué es una buena manera de pensar\(\operatorname{Pr}\left\{\bigcap_{m} \bigcup_{n \geq m} A_{n}\right\}\). Pista: Considera una ω que está contenida en algún número finito\(k\) de los conjuntos\(A_{n}\) y argumenta que debe haber un entero\(m\) tal que\(\omega \notin A_{n}\) para todos\(n>m\).

Ejercicio 4.8

\(\left\{X_{i} ; i \geq 1\right\}\)Dejen ser los intervalos entre renovaciones de un proceso de renovación y supongamos que\(\mathrm{E}\left[X_{i}\right]=\infty\). Dejar\(b>0\) ser un número arbitrario y\(\breve{X}_{i}\) ser una variable aleatoria truncada definida por\(\breve{X}_{i}=X_{i}\) si\(X_{i} \leq b\) y de\(\breve{X}_{i}=b\) otra manera.

1. Demostrar que para cualquier constante\(M>0\), hay una\(b\) suficientemente grande para que\(\mathrm{E}\left[\breve{X}_{i}\right] \geq M\).
2. Que\(\{\breve{N}(t) ; t \geq 0\}\) sea el proceso de conteo de renovaciones con intervalos entre renovaciones\(\left\{\breve{X}_{i} ; i \geq 1\right\}\) y demuestre que para todos\(t>0\),\(\breve{N}(t) \geq N(t)\).
3. Mostrar que para todas las funciones de muestra\(N(t, \omega)\), excepto un conjunto de probabilidad 0,\(N(t, \omega) / t<2 / M\) para todas las t suficientemente grandes Nota: Dado que\(M\) es arbitrario, esto significa que\(\lim N(t) / t=0\) con probabilidad 1.

Ejercicio 4.9

Dejar\(Y(t)=S_{N(t)+1}-t\) ser la vida residual en el tiempo t de un proceso de renovación. Primero considere un proceso de renovación en el que el tiempo entre llegadas tenga densidad\(\mathrm{f}_{X}(x)=e^{-x} ; x \geq 0\), y luego considere un proceso de renovación con densidad

\(\mathrm{f}_{X}(x)=\frac{3}{(x+1)^{4}} ; \quad x \geq 0\)

Para cada una de las densidades anteriores, use la teoría de renovación-recompensa para encontrar:

1. el promedio de tiempo de\(Y(t)\)
2. el segundo momento en el tiempo de\(Y(t)\) (i.e.,\(\lim _{T \rightarrow \infty} \frac{1}{T} \int_{0}^{T} Y^{2}(t) d t\))

Para la densidad exponencial, verifica tus respuestas encontrando\(\mathrm{E}[Y(t)]\) y\(\mathrm{E}\left[Y^{2}(t)\right]\) directamente.

Ejercicio 4.10

Considere una variación de un sistema de colas M/G/1 en el que no hay facilidad para salvar a los clientes que esperan. Supongamos que los clientes llegan de acuerdo a un proceso de tarifa de Poisson\(\lambda\). Si el servidor está ocupado, el cliente sale y se pierde para siempre; si el servidor no está ocupado, el cliente ingresa al servicio con una función de distribución del tiempo de servicio indicada por\(\mathrm{F}_{Y}(y)\).

Los tiempos sucesivos de servicio (para aquellos clientes que son atendidos) son IID e independientes de los tiempos de llegada. Supongamos que el cliente número 0 llega e ingresa al servicio en el momento\(t=0\).

1. Mostrar que la secuencia de tiempos\(S_{1}, S_{2}, \ldots\) en los que los clientes sucesivos ingresan al servicio son los tiempos de renovación de un proceso de renovación. Mostrar que cada intervalo inter-renovación\(X_{i}=S_{i}-S_{i-1}\) (donde\(S_{0}=0\)) es la suma de dos variables aleatorias independientes,\(Y_{i}+U_{i}\) donde\(Y_{i}\) es el tiempo de servicio\(i\) th; encontrar la densidad de probabilidad de\(U_{i}\).
2. Supongamos que se incurre en una recompensa (en realidad un costo en este caso) de una unidad por cada cliente rechazado. Esboce la función de recompensa esperada en función del tiempo para la función de muestra de intervalos entre renovaciones e intervalos de servicio que se muestran a continuación; la expectativa es hacerse cargo de aquellas llegadas (no mostradas) de clientes que deben ser rechazadas.

   

3. Dejar\(\int_{0}^{t} R(\tau) d \tau\) denotar la recompensa acumulada (es decir, costo) de 0 a\(t\) y encontrar el límite a partir\(t \rightarrow \infty\) de\((1 / t) \int_{0}^{t} R(\tau) d \tau\). Explicar (sin ningún intento de ser riguroso o formal) por qué existe este límite con probabilidad 1.
4. En el límite de grandes\(t\), encuentra la recompensa esperada desde el tiempo\(t\) hasta la próxima renovación. Pista: Dibuje esta recompensa esperada en función de\(t\) para una muestra dada de intervalos entre renovaciones e intervalos de servicio; luego encuentre el promedio de tiempo.
5. Ahora supongamos que las llegadas son deterministas, con la primera llegada a la hora 0 y la\(n\) ésima llegada a la hora\(n-1\). ¿La secuencia de tiempos\(S_{1}, S_{2}, \ldots\) en los que los clientes posteriores inician el servicio aún constituyen los tiempos de renovación de un proceso de renovación? Dibuje un boceto de llegadas, salidas e intervalos de tiempo de servicio. Nuevamente encuentra\(\lim _{t \rightarrow \infty}\left(\int_{0}^{t} R(\tau) d \tau\right) / t\).

Ejercicio 4.11

\(Z(t)=t-S_{N(t)}\)Sea la edad de un proceso de renovación y\(Y(t)=S_{N(t)+1}-t\) sea la vida residual. \(\mathrm{F}_{X}(x)\)Sea la función de distribución del intervalo inter-renovación y encuentre lo siguiente en función de\(\mathrm{F}_{X}(x)\):

1. \(\operatorname{Pr}\{Y(t)>x \mid Z(t)=s\}\)
2. \(\operatorname{Pr}\{Y(t)>x \mid Z(t+x / 2)=s\}\)
3. \(\operatorname{Pr}\{Y(t)>x \mid Z(t+x)>s\}\)para un proceso de Poisson.

Ejercicio 4.12

\(\mathrm{F}_{Z}(z)\)Sea la fracción de tiempo (sobre el intervalo limitante\((0, \infty)\) que la edad de un proceso de renovación es como máximo\(z\). Demostrar que\(\mathrm{F}_{Z}(z)\) satisface

\(\mathrm{F}_{Z}(z)=\frac{1}{\overline{X}} \int_{x=0}^{y} \operatorname{Pr}\{X>x\} d x \quad \text { WP1 }\)

Sugerencia: Siga el argumento en el Ejemplo 4.4.5.

Ejercicio 4.13

1. Dejar\(J\) ser una regla de detención y\(\mathbb{I}_{\{J \geq n\}}\) ser la variable aleatoria indicadora del evento\(\{J \geq n\}\). \(J=\sum_{n \geq 1} \mathbb{I}_{\{J \geq n}\)Demuéstralo.
2. Mostrar eso\(\mathbb{I}_{J \geq 1} \geq \mathbb{I}_{J \geq 2} \geq \ldots\), es decir, mostrar eso\(n>1, \mathbb{I}_{J \geq n}(\omega) \geq \mathbb{I}_{J \geq n+1}(\omega)\) para cada uno\(\omega \in \Omega\) (excepto quizás por un conjunto de probabilidad 0).

Ejercicio 4.14

1. Utilice la igualdad de Wald para calcular el número esperado de ensayos de un proceso de Bernoulli hasta e incluyendo el éxito\(k\) th.
2. Utilizar medios elementales para encontrar el número esperado de ensayos hasta e incluyendo el primer éxito. Use esto para encontrar el número esperado de ensayos hasta e incluyendo el éxito\(k\) th. Comparar con la parte a).

Ejercicio 4.15

Un jugador con un capital finito inicial de\(d>0\) dólares comienza a jugar una máquina tragaperras de dólares. En cada jugada, o su dólar se pierde o se devuelve con algún número adicional de dólares. Que\(X_{i}\) sea su cambio de capital en la\(i\) th play. Supongamos que\(\left\{X_{i} ; i=1,2, \ldots\right\}\) es un conjunto de variables aleatorias IID que toman valores enteros {−1, 0, 1,.}. Asumir eso\(\mathrm{E}\left[X_{i}\right]<0\). El jugador juega hasta perder todo su dinero (es decir, los\(d\) dólares iniciales más las ganancias posteriores).

1. \(J\)Sea el número de jugadas hasta que el jugador pierda todo su dinero. ¿Es suficiente la débil ley de los grandes números para argumentar eso\(\lim _{n \rightarrow \infty} \operatorname{Pr}\{J>n\}=0\) (es decir, esa\(J\) es una variable aleatoria) o es necesaria la ley fuerte?
2. Encuentra\(\mathrm{E}[J]\). Sugerencia: El hecho de que solo haya un posible resultado negativo es importante aquí.

Ejercicio 4.16

Let\(\left\{X_{i} ; i \geq 1\right\}\) Ser IID variables aleatorias binarias con\(P_{X}(0)=P_{X}(1)=1/2\). Dejar\(J\) ser una variable aleatoria de valor entero positivo definida en el espacio muestral anterior de secuencias binarias y let\(S_{J}=\sum_{i=1}^{J} X_{i}\). Encuentra el ejemplo más sencillo que puedas en el que no\(J\) es un juicio de detención para\(\left\{X_{i} ; i \geq 1\right\}\) y dónde\(\mathrm{E}[X] \mathrm{E}[J] \neq \mathrm{E}\left[S_{J}\right]\). Sugerencia: Intenta dejar\(J\) asumir solo los valores 1 y 2.

Ejercicio 4.17

Let\(J=\min \left\{n \mid S_{n} \leq b \text { or } S_{n} \geq a\right\}\), donde\(a\) es un entero positivo,\(b\) es un entero negativo, y\(S_{n}=X_{1}+X_{2}+\cdots+X_{n}\). Supongamos que\(\left\{X_{i} ; i \geq 1\right\}\) es un conjunto de IID rv medio cero que puede tomar solo el conjunto de valores {−1, 0, +1}, cada uno con probabilidad positiva.

1. ¿Es\(J\) una regla de detención? ¿Por qué o por qué no? Pista: La parte más difícil de esto es argumentar que\(J\) es una variable aleatoria (es decir, no defectuosa); no es necesario construir una prueba de ello, sino tratar de argumentar por qué debe ser verdad.
2. ¿Cuáles son los valores posibles de\(S_{J}\)?
3. Encuentra una expresión para\(\mathrm{E}\left[S_{J}\right]\) en términos de\(p, a\), y\(b\), dónde\(p=\operatorname{Pr}\left\{S_{J} \geq a\right\}\).
4. Encuentra una expresión\(\mathrm{E}\left[S_{J}\right]\) de la igualdad de Wald. Usa esto para resolver para\(p\).

Ejercicio 4.18

Demostrar que el intercambio de expectativa y suma en\ ref {4.32} es válido si\(\mathrm{E}[J]<\infty\). Sugerencia: Primero exprese la suma como\(\sum_{n=1}^{k-1} X_{n} \mathbb{I}_{J \geq n}+\sum_{n=k}^{\infty}\left(X_{n}^{+}+X_{n}^{-}\right) \mathbb{I}_{J \geq n}\) y luego considere el límite como\(k \rightarrow \infty\).

Ejercicio 4.19

Considera un minero amnésico atrapado en una habitación que contiene tres puertas. La puerta 1 lo lleva a la libertad después de dos días de viaje; la puerta 2 lo devuelve a su habitación después de cuatro días de viaje; y la puerta 3 lo devuelve a su habitación después de ocho días de viaje. Supongamos que cada puerta es igualmente probable que se elija cada vez que esté en la habitación, y dejar\(T\) denotar el tiempo que tarda el minero en liberarse.

1. Definir una secuencia de variables aleatorias independientes e idénticamente distribuidas\(X_{1}, X_{2}, \ldots\) y una regla de detención\(J\) tal que

   \(T=\sum_{i=1}^{J} X_{i}\).

2. Usa la igualdad de Wald para encontrar\(\mathrm{E}[T]\).
3. Calcular\(\mathrm{E}\left[\sum_{i=1}^{J} X_{i} \mid J=n\right]\) y demostrar que no es igual a\(\mathrm{E}\left[\sum_{i=1}^{n} X_{i}\right]\).
4. Utilice la parte c) para una segunda derivación de\(\mathrm{E}[T]\).

Ejercicio 4.20

1. Considerar un proceso de renovación para el cual los intervalos entre renovaciones tengan el PMF\(p_{X}(1)=p_{X}(2)=1 / 2\). Use combinatorias elementales para mostrar eso\(m(1)=1 / 2\),\(m(2)=5 / 4\), y\(m(3)=15 / 8\).
2. Use medios elementales para mostrar eso\(\mathrm{E}\left[S_{N(1)}\right]=1 / 2\) y\(\mathrm{E}\left[S_{N(1)+1}\right]=9 / 4\). Verificar\ ref {4.35} en este caso (es decir, para\(t=1\)) y mostrar que no\(N(1)\) es un juicio detenido. Obsérvese también que la duración esperada, no\(\mathrm{E}\left[S_{N(1)+1}-S_{N(1)}\right]\) es igual a\(\overline{X}\).
3. Considerar una forma más general de la parte a) dónde\(\operatorname{Pr}\{X=1\}=1-p\) y\(\operatorname{Pr}\{X=2\}=p\). Dejar\(\operatorname{Pr}\left\{W_{n}=1\right\}=x_{n}\) y mostrar que\(x_{n}\) satisface la ecuación de diferencia\(x_{n}=1-p x_{n-1}\) para\(n \geq 1\) donde por convención\(x_{0}=1\). Usa esto para demostrar que

   \[x_{n}=\frac{1-(-p)^{n+1}}{1+p}\label{4.112} \]

   A partir de esto, resolver\(m(n)\) para\(n \geq 1\).

Ejercicio 4.21

Dejar\(\{N(t) ; t>0\}\) ser un proceso de conteo de renovación generalizado para permitir intervalos\(\left\{X_{i}\right\}\) de inter-renovación de duración 0. Que cada uno\(X_{i}\) tenga el PMF\(\operatorname{Pr}\left\{X_{i}=0\right\}=1-\epsilon\);\(\operatorname{Pr}\left\{X_{i}=1 / \epsilon\right\}=\epsilon\).

1. Dibuje una función típica de muestra de\(\{N(t) ; t>0\}\). Tenga en cuenta que\(N(0)\) puede ser distinto de cero (\(N(0)\)es decir, es el número de tiempos cero entre llegadas que ocurren antes del primer tiempo interllegada distinto de cero).
2. \(\mathrm{E}[N(t)]\)Evaluar en función de\(t\).
3. Sketch\(\mathrm{E}[N(t)] / t\) en función de\(t\).
4. Evalúa\(\mathrm{E}\left[S_{N(t)+1}\right]\) en función de\(t\) (haz esto directamente, y luego usa la igualdad de Wald como control de tu trabajo).
5. Dibuje el límite inferior\(\mathrm{E}[N(t)] / t \geq 1 / \mathrm{E}[X]-1 / t\) en la misma gráfica con la parte c).
6. Sketch\(\mathrm{E}\left[S_{N(t)+1}-t\right]\) en función de\(t\) y encontrar el promedio de tiempo de esta cantidad.
7. Evaluar\(\mathrm{E}\left[S_{N(t)}\right]\) como una función de t; verificar eso\(\mathrm{E}\left[S_{N(t)}\right] \neq \mathrm{E}[X] \mathrm{E}[N(t)]\).

Ejercicio 4.22

Dejar\(\{N(t) ; t>0\}\) ser un proceso de conteo de renovación y dejar que\(m(t)=\mathrm{E}[N(t)]\) sea el número esperado de llegadas hasta e incluyendo el tiempo\(t\). Seamos\(\left\{X_{i} ; i \geq 1\right\}\) los tiempos de inter-renovación y asumamos eso\(\mathrm{F}_{X}(0)=0\).

1. Para todos\(x>0\) y\(t>x\) demuéstralo\(\mathrm{E}\left[N(t) \mid X_{1}=x\right]=\mathrm{E}[N(t-x)]+1\).
2. Use la parte a) para mostrar eso\(m(t)=\mathrm{F}_{X}(t)+\int_{0}^{t} m(t-x) d \mathrm{~F}_{X}(x)\) para\(t>0\). Esta ecuación es la ecuación de renovación derivada de manera diferente en (4.52).
3. Supongamos que\(X\) es una variable aleatoria exponencial de parámetro\(\lambda\). Evaluar\(L_{m}(s)\) a partir de (4.54); verificar que la transformada inversa de Laplace es\(\lambda t\);\(t \geq 0\).

Ejercicio 4.23

1. Que el intervalo entre renovaciones de un proceso de renovación tenga una densidad Erlang de segundo orden,\(f_{X}(x)=\lambda^{2} x \exp (-\lambda x)\). Evaluar la transformación de Laplace de\(m(t)=\mathrm{E}[N(t)]\).
2. Utilice esto para evaluar\(m(t)\) para\(t \geq 0\). Verifica que tu respuesta esté de acuerdo con (4.56).
3. Evaluar la pendiente de\(m(t)\) at\(t=0\) y explicar por qué esa pendiente no es sorprendente.
4. Vea las renovaciones aquí como las llegadas pares en un proceso de tasa de Poisson\(\lambda\). Haga un boceto\(m(t)\) para el proceso aquí y muestre la mitad del número esperado de llegadas para el proceso de Poisson en el mismo boceto. Explique la diferencia entre los dos.

Ejercicio 4.24

1. \(N(t)\)Sea el número de llegadas en el intervalo\((0, t]\) para un proceso de Poisson de tasa\(\lambda\). Demostrar que la probabilidad de que\(N(t)\) sea par es\([1+\exp (-2 \lambda t)] / 2\). Pista: Mira la expansión de la serie power de\(\exp (-\lambda t)\) y la de\(\exp (\lambda t)\), y mira la suma de las dos. Compárelo con\(\sum_{n \text { even }} \operatorname{Pr}\{N(t)=n\}\)
2. \(\tilde{N}(t)\)Sea el número de llegadas pares en\((0, t]\). Mostrar que\(\tilde{N}(t)=N(t) / 2-\mathbb{I}_{\text {odd }}(t) / 2 \text { where } \mathbb{I}_{\text {odd }}(t)\) es una variable aleatoria que es 1 si\(N(t)\) es impar y 0 en caso contrario.
3. Utilice las partes a) y b) para encontrar\(\mathrm{E}[\tilde{N}(t)]\). Tenga en cuenta que esto es\(m(t)\) para un proceso de renovación con intervalos entre renovaciones de Erlang de 2do orden.

Ejercicio 4.25

1. Considere una función\(r(z) \geq 0\) definida de la siguiente manera para\(0 \leq z<\infty\): Para cada entero\(n \geq 1\) y cada entero\(k\),\(1 \leq k<n, r(z)=1\) para\(n+k / n \leq z \leq n+k / n+2^{-n}\). Para todos los demás\(z\),\(r(z)=0\). Esbozar esta función y mostrar que no\(r(z)\) es directamente integrable Riemann.
2. Evaluar la integral de Riemann\(\int_{0}^{\infty} r(z) d z\).
3. Supongamos que\(r(z)\) está disminuyendo, es decir, eso\(r(z) \geq r(y)\) para todos\(y>z>0\). Mostrar tht si Riemann\(r(z)\) es integrable, también es directamente Riemann integrable.
4. Supongamos\(f(z) \geq 0\), definido para\(z \geq 0\), es decreciente y Riemann integrable y eso\(f(z) \geq r(z)\) para todos\(z \geq 0\). Demostrar que\(r(z)\) es Directamente Riemann integrable.
5. Dejar\(X\) ser un rv no negativo para el cual\(\mathrm{E}\left[X^{2}\right]<\infty\). Demostrar que\(x \mathrm{~F}_{X}^{\mathrm{c}}(x)\) es directamente Riemann integrable. Pista: Considere\(y \mathrm{~F}_{X}^{\mathrm{c}}(y)+\int_{y}^{\infty} \mathrm{F}_{X}(x) d x\) y use la Figura 1.7 (o use la integración por partes) para mostrar que esta expresión está disminuyendo en\(y\).

Ejercicio 4.26

Dejar\(Z(t), Y(t), \widetilde{X}(t)\) denotar la edad, la vida residual, y la duración en el tiempo\(t\) para un proceso de recuento de renovación\(\{N(t) ; t>0\}\) en el que el tiempo de interllegada tiene una densidad dada por\(f(x)\). Encuentre las siguientes densidades de probabilidad; asuma el estado estacionario.

1. \(\mathrm{f}_{Y(t)}(y \mid Z(t+s / 2)=s)\)para dado\(s>0\).
2. \(\mathrm{f}_{Y(t), Z(t)}(y, z)\).
3. \(\mathrm{f}_{Y(t)}(y \mid \widetilde{X}(t)=x)\).
4. \(\mathrm{f}_{Z(t)}(z \mid Y(t-s / 2)=s)\)para dado\(s>0\).
5. \(\mathrm{f}_{Y(t)}(y \mid Z(t+s / 2) \geq s)\)para dado\(s>0\).

Ejercicio 4.27

1. Encuentre\(\lim _{t \rightarrow \infty}\{\mathrm{E}[N(t)]-t / \overline{X}\}\) para un proceso de conteo de renovaciones\(\{N(t) ; t>0\}\) con tiempos de inter-renovación\(\left\{X_{i} ; i \geq 1\right\}\). Pista: usa la ecuación de Wald.
2. Evalúa tu resultado para el caso en el que\(X\) se encuentre una variable aleatoria exponencial (ya sabes cuál debería ser el resultado en este caso).
3. Evalúa tu resultado para un caso en el que\(\mathrm{E}[X]<\infty\) y\(\mathrm{E}\left[X^{2}\right]=\infty\). Explique (muy brevemente) por qué esto no contradice el teorema de renovación elemental.

Ejercicio 4.28

Los clientes llegan a una parada de autobús de acuerdo con un proceso de tarifa de Poisson\(\lambda\). Independientemente, los autobuses llegan de acuerdo a un proceso de renovación con la distribución de intervalos entre renovaciones\(\mathrm{F}_{X}(x)\). En la época de la llegada de un autobús, todos los pasajeros que esperan ingresan al autobús y el autobús sale de inmediato. Deje\(R(t)\) ser el número de clientes que esperan a tiempo\(t\).

1. Dibujar un boceto de una función de muestra de\(R(t)\).
2. Dado que el primer autobús llega a tiempo\(X_{1}=x\), encuentra el número esperado de clientes recogidos; luego encuentra\(\mathrm{E}\left[\int_{0}^{x} R(t) d t\right]\), nuevamente dada la llegada del primer autobús a las\(X_{1}=x\).
3. Encontrar\(\lim _{t \rightarrow \infty} \frac{1}{t} \int_{0}^{t} R(\tau) d \tau\) (con probabilidad 1). Suponiendo que\(\mathrm{F}_{X}\) es una distribución no aritmética, encuentra\(\lim _{t \rightarrow \infty} \mathrm{E}[R(t)]\). Interpreta lo que significan estas cantidades.
4. Utilice la parte c) para encontrar el promedio de tiempo de espera esperado por cliente.
5. Encuentra la fracción de tiempo que no hay clientes en la parada de autobús. (Sugerencia: esta parte es independiente de a), b) y c); verifique su respuesta para\(\mathrm{E}[X] \ll 1 / \lambda\)).

Ejercicio 4.29

Considere la misma configuración que en el Ejercicio 4.28 excepto que ahora los clientes llegan de acuerdo con un proceso de renovación no aritmética independiente del proceso de llegada del autobús. \(1 / \lambda\)Sea el intervalo entre renovaciones esperadas para el proceso de renovación del cliente. Supongamos que ambos procesos de renovación están en estado estacionario (es decir, o solo miramos\(t \gg 0\), o asumimos que son procesos de equilibrio). Dado que el enésimo cliente llega a tiempo\(t\), encuentra la espera esperada para el cliente\(n\). Encuentra la espera esperada para el cliente\(n\) sin condicionar a la hora de llegada.

Ejercicio 4.30

Dejar\(\left\{N_{1}(t) ; t>0\right\}\) ser un proceso de conteo de Poisson de tasa\(\lambda\). Supongamos que las llegadas de este proceso son encendidas y desactivadas por las llegadas de un proceso de conteo de renovación no aritmética\(\left\{N_{2}(t) ; t>0\right\}\) (ver figura a continuación). Los dos procesos son independientes.

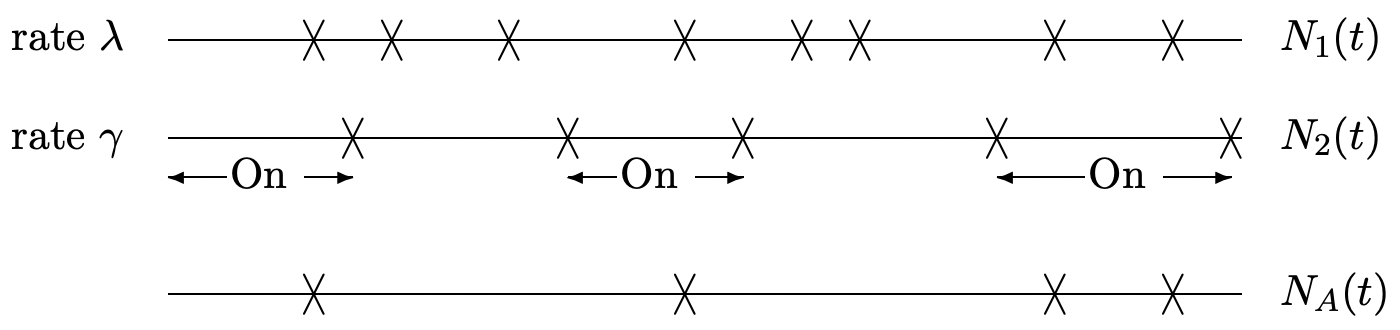
\(\left\{N_{A}(t) ; t \geq 0\right\}\)Sea el proceso conmutado; es decir,\(N_{A}(t)\) incluye llegadas desde\(\{N_{1}(t) ; t>0\}\) while\(N_{2}(t)\) es par y excluye llegadas de\(\left\{N_{1}(t) ; t>0\right\}\) while\(N_{2}(t)\) es impar.

1. ¿Es\(N_{A}(t)\) un proceso de conteo de renovación? Explica tu respuesta y si no estás seguro, mira varios ejemplos para\(N_{2}(t)\).
2. Encuentra\(\lim _{t \rightarrow \infty} \frac{1}{t} N_{A}(t)\) y explica por qué existe el límite con probabilidad 1. Sugerencia: Usa la simetría, es decir, mira\(N_{1}(t)-N_{A}(t)\). Para mostrar por qué existe el límite, utilice el teorema de renewalreward. ¿Cuál es el proceso de renovación adecuado para usar aquí?
3. Ahora supongamos que\(\left\{N_{1}(t) ; t>0\right\}\) es un proceso de conteo de renovación no aritmética pero no un proceso de Poisson y dejar que el intervalo entre renovaciones esperado sea\(1 / \lambda\). Para cualquier δ dado, encuentra\(\lim _{t \rightarrow \infty} \mathrm{E}\left[N_{A}(t+\delta)-N_{A}(t)\right]\) y explica tu razonamiento. ¿Por qué su argumento en\ ref {b} no logra demostrar un promedio de tiempo para este caso?

Ejercicio 4.31

Una cola M/G/1 tiene llegadas a tarifa\(\lambda\) y una distribución del tiempo de servicio dada por\(\mathrm{F}_{Y}(y)\). Asumir eso\(\lambda<1 / \mathrm{E}[Y]\). Épocas en las que el sistema se vacía definen un proceso de renovación. \(\mathrm{F}_{Z}(z)\)Sea la distribución de los intervalos entre renovaciones y deje\(\mathrm{E}[Z]\) ser el intervalo interrenovador medio.

1. Encuentra la fracción de tiempo que el sistema está vacío en función de\(\lambda\) y\(\mathrm{E}[Z]\). Exponga cuidadosamente lo que quiere decir con tal fracción.
2. Aplicar el teorema de Little, no al sistema en su conjunto, sino al número de clientes en el servidor (es decir, 0 o 1). Use esto para encontrar la fracción de tiempo que el servidor está ocupado.
3. Combine sus resultados en a) y b) para encontrar\(\mathrm{E}[Z]\) en términos de\(\lambda\) y\(\mathrm{E}[Y]\); dar la fracción de tiempo que el sistema está inactivo en términos de\(\lambda\) y\(\mathrm{E}[Y]\).
4. Encuentra la duración esperada de un periodo ocupado.

Ejercicio 4.32

Considere una secuencia\(X_{1}, X_{2}, \ldots\) de variables aleatorias binarias IID. Dejar\(p\) y\(1-p\) denotar\(\operatorname{Pr}\left\{X_{m}=1\right\}\) y\(\operatorname{Pr}\left\{X_{m}=0\right\}\) respectivamente. Se dice que una renovación ocurre en el momento\(m\) si\(X_{m-1}=0\) y\(X_{m}=1\).

1. Demostrar que\(\{N(m) ; m \geq 0\}\) es un proceso de conteo de renovaciones donde\(N(m)\) está el número de renovaciones hasta e incluyendo el tiempo\(m\)\(N(0)\) y y\(N(1)\) se toman para ser 0.
2. ¿Cuál es la probabilidad de que se produzca una renovación en el momento\(m\),\(m \geq 2\)?
3. Encuentra el intervalo entre renovaciones esperado; usa el teorema de Blackwell aquí.
4. Ahora cambia la definición de renovación; ahora se produce una renovación en el momento\(m\) si\(X_{m-1}=1\) y\(X_{m}=1\). Demostrar que\(\left\{N_{m}^{*} ; m \geq 0\right\}\) es un proceso de conteo de renovación retrasada donde\(N_{m}^{*}\) está el número de renovaciones hasta e incluyendo\(m\) para esta nueva definición de renovación\(\left(N_{0}^{*}=N_{1}^{*}=0\right)\).
5. Encuentre el intervalo entre renovaciones esperado para las renovaciones de la parte d).
6. Dado que en el momento se produce una renovación (de acuerdo con la definición de la letra d))\(m\), encontrar el tiempo esperado hasta la siguiente renovación, condicional, primero, encendido\(X_{m+1}=1\) y, siguiente, encendido\(X_{m+1}=0\). Sugerencia: use el resultado en e) más el resultado para\(X_{m+1}=1\) para el acondicionamiento encendido\(X_{m+1}=0\).
7. Usa tu resultado en f) para encontrar el intervalo esperado desde el tiempo 0 hasta la primera renovación de acuerdo con la definición de renovación en d).
8. Qué patrón requiere un tiempo esperado mayor para ocurrir: 0011 o 0101
9. ¿Cuál es el tiempo esperado hasta la primera ocurrencia de 0111111?

Ejercicio 4.33

Un sistema grande es controlado por computadoras\(n\) idénticas. Cada computadora alterna independientemente entre un estado operativo y un estado de reparación. La duración del estado operativo, desde la finalización de una reparación hasta la siguiente necesidad de reparación, es una variable aleatoria\(X\) con duración finita esperada\(\mathrm{E}[X]\). El tiempo requerido para reparar una computadora es una variable aleatoria distribuida exponencialmente con densidad\(\lambda e^{-\lambda t}\). Todas las duraciones de operación y las duraciones de reparación son independientes. Supongamos que todas las computadoras están en el estado de reparación en el tiempo 0.

1. Para una sola computadora, digamos la\(i\) th, ¿las épocas en las que la computadora ingresa al estado de reparación forman un proceso de renovación? Si es así, encuentra el intervalo entre renovaciones esperado.
2. ¿Las épocas en las que ingresa al estado operativo forman un proceso de renovación?
3. Encuentra la fracción de tiempo durante la cual la\(i\) computadora está operativa y explica a qué te refieres con fracción de tiempo.
4. \(Q_{i}(t)\)Sea la probabilidad de que la i-ésima computadora esté operativa en el momento\(t\) y encuentre\(\lim _{t \rightarrow \infty} Q_{i}(t)\).
5. El sistema está en modo de falla en un momento dado si todas las computadoras están en el estado de reparación en ese momento. ¿Las épocas en las que comienzan los modos de falla del sistema forman un proceso de renovación?
6. \(\operatorname{Pr}\{t\}\)Sea la probabilidad de que el sistema esté en modo de falla en el momento\(t\). Encuentra\(\lim _{t \rightarrow \infty} \operatorname{Pr}\{t\}\). Pista: mira la parte d).
7. Para δ small, encuentre la probabilidad de que el sistema entre en modo de falla en el intervalo\((t, t+\delta]\) en el límite como\(t \rightarrow \infty\).
8. Encuentre el tiempo esperado entre entradas sucesivas en modo de falla.
9. A continuación supongamos que el tiempo de reparación de cada computadora tiene una densidad arbitraria en lugar de exponencial, pero tiene un tiempo medio de reparación de\(1 / \lambda\). ¿Las épocas en las que comienzan los modos de falla del sistema forman un proceso de renovación?
10. Repetir la parte f) para el supuesto en (i).

Ejercicio 4.34

Dejar\(\left\{N_{1}(t) ; t>0\right\}\) y\(\left\{N_{2}(t) ; t>0\right\}\) ser procesos independientes de conteo de renovación. Supongamos que cada uno tiene la misma función de distribución\(\mathrm{F}(x)\) para los intervalos entre llegadas y asume que\(f(x)\) existe una densidad para los intervalos entre llegadas.

1. ¿El proceso de conteo es\(\left\{N_{1}(t)+N_{2}(t) ; t>0\right\}\) un proceso de conteo de renovación? Explique.
2. Dejar\(Y(t)\) ser el intervalo desde\(t\) hasta la primera llegada (de cualquiera de los dos procesos) después\(t\). Encuentra una expresión para la función de distribución de\(Y(t)\) en el límite\(t \rightarrow \infty\) (puedes suponer que los promedios de tiempo y los promedios del conjunto son los mismos).
3. Supongamos que una recompensa\(R\) de tarifa 1 unidad por segundo comienza a ganarse cada vez que ocurre una llegada del proceso 1 y deja de ganarse cada vez que ocurre una llegada del proceso 2.

   Supongamos que\(\lim _{t \rightarrow \infty}(1 / t) \int_{0}^{t} R(\tau) d \tau\) existe con probabilidad 1 y encuentra su valor numérico.

4. Dejar\(Z(t)\) ser el intervalo desde\(t\) hasta la primera vez después de\(t\) eso\(R(t)\) (como en la parte c) cambia de valor. Encuentra una expresión para\(\mathrm{E}[Z(t)]\) en el límite\(t \rightarrow \infty\). Sugerencia: Asegúrese de entender por qué no\(Z(t)\) es lo mismo que\(Y(t)\) en la parte b). Puede que le resulte más fácil encontrar primero la expectativa de\(Z(t)\) condicional tanto a la duración del intervalo\(\left\{N_{1}(t) ; t>0\right\}\) entre llegadas que contiene\(t\) como a la duración del intervalo\(\left\{N_{2}(t) ; t \geq 0\right\}\) entre llegadas que contiene\(t\); ¡dibuja imágenes!

Ejercicio 4.35

Este problema proporciona otra forma de tratar los promedios de conjunto para los problemas de renovaciónrecompensa. Supongamos por simplicidad notacional que\(X\) es una variable aleatoria continua.

1. Demuestre que\(\operatorname{Pr}\{\text { one or more arrivals in }(\tau, \tau+\delta)\}=m(\tau+\delta)-m(\tau)-o(\delta)\) dónde\(o(\delta) \geq 0\) y\(\lim _{\delta \rightarrow 0} o(\delta) / \delta=0\).
2. Demostrar que\(\operatorname{Pr}\{Z(t) \in[z, z+\delta), \tilde{X}(t) \in(x, x+\delta)\}\) es igual a\([m(t-z)-m(t-z-\delta)-o(\delta)]\left[\mathrm{F}_{X}(x+\delta)-\mathrm{F}_{X}(x)\right] \text { for } x \geq z+\delta\).
3. Suponiendo que eso\(m^{\prime}(\tau)=d m(\tau) / d \tau\) existe para todos\(\tau\), demostrar que la densidad conjunta de\(Z(t)\),\(\widetilde{X}(t)\) es\(\mathrm{f}_{Z(t), \tilde{X}(t)}(z, x)=m^{\prime}(t-z) \mathrm{f}_{X}(x)\) para\(x>z\).
4. Demostrar que\(\mathrm{E}[R(t)]=\int_{z=0}^{t} \int_{x=z}^{\infty} \mathcal{R}(z, x) \mathrm{f}_{X}(x) d x m^{\prime}(t-z) d z\)

Ejercicio 4.36

Este problema está diseñado para darte una forma alternativa de ver ensembleaverage para problemas de renovación-recompensa. Primero encontramos una expresión exacta para\(\operatorname{Pr}\left\{S_{N(t)}>s\right\}\). Encontramos esto por arbitrario\(s\) y\(t\),\(0<s<t\).

1. Al dividir el evento\(\left\{S_{N(t)}>s\right\}\) en subeventos\(\left\{S_{N(t)}>s, N(t)=n\right\}\), explique cada uno de los siguientes pasos:

   \ (\ begin {alineado}
   \ nombreoperador {Pr}\ izquierda\ {S_ {N (t)} >s\ derecha\} &=\ sum_ {n=1} ^ {\ infty}\ nombreoperador {Pr}\ izquierda\ {t\ geq S_ {n} >s, S_ {n+1} >t\ derecha\}\
   &=\ sum_ {n=1} {\ infty}\ int_ {y=s} ^ {t}\ nombreoperador {Pr}\ izquierda\ {S_ {n+1} >t\ mediados S_ {n} =y\ derecha\} d\ mathrm {~F} _ {S_ {n}} (y)\\
   &=\ int_ {y=s} ^ {t}\ mathrm {~F} _ {X} ^ {c} (t-y) d\ sum_ {n=1} ^ {\ infty}\ mathrm {F} _ {S_ {n}} (y)\\
   &=\ int_ {y=s} ^ {t}\ mathrm {~F} _ _ {X} {^ c} (t-y) d m (y)\ quad\ texto {donde} m (y) =\ mathrm {E} [N (y)]
   \ final {alineado}\)

2. Demostrar que para\(0<s<t<u\),

   \(\operatorname{Pr}\left\{S_{N(t)}>s, S_{N(t)+1}>u\right\}=\int_{y=s}^{t} \mathrm{~F}_{X}^{c}(u-y) d m(y)\)

3. Dibuja un boceto bidimensional, con la edad y la duración como ejes, y mostrar la región de los valores (edad, duración) correspondientes al evento\(\left\{S_{N}(t)>s, S_{N(t)+1}>u\right\}\).
4. Supongamos que para grandes\(t\), se\(d m(y)\) puede aproximar (según Blackwell) como\((1 / \overline{X}) d y\), donde\(\overline{X}=\mathrm{E}[X]\). Suponiendo que\(X\) también tenga una densidad, utilice el resultado en las partes b) y c) para encontrar la densidad articular de edad y duración.

Ejercicio 4.37

En este problema, mostramos cómo calcular la distribución de la vida residual\(Y(t)\) como transitoria en\(t\). Que\(\mu(t)=d m(t) / d t\) donde\(m(t)=\mathrm{E}[N(t)]\), y que la distribución entre llegadas tenga la densidad\(f_{X}(x)\). Dejemos\(Y(t)\) tener la densidad\(f_{Y(t)}(y)\).

1. Demostrar que estas densidades están relacionadas por la ecuación integral

   \(\mu(t+y)=\mathrm{f}_{Y(t)}(y)+\int_{u=0}^{y} \mu(t+u) \mathrm{f}_{X}(y-u) d u\)

2. Dejar\(L_{\mu, t}(r)=\int_{y \geq 0} \mu(t+y) e^{-r y} d y\) y dejar\(L_{Y(t)}(r)\) y\(L_{X}(r)\) ser el Laplace transforma de\(f_{Y(t)}(y)\) y\(\mathrm{f}_{X}(x)\) respectivamente. Encontrar\(L_{Y(t)}(r)\) en función de\(L_{\mu, t}\) y\(L_{X}\).
3. Considere la densidad inter-renovación\(\mathrm{f}_{X}(x)=(1 / 2) e^{-x}+e^{-2 x}\) para\(x \geq 0\) (como en el Ejemplo 4.6.1). Encuentra\(L_{\mu, t}(r)\) y\(L_{Y(t)}(r)\) para este ejemplo.
4. Encuentra\(f_{Y(t)}(y)\). Demuestre que su respuesta se reduce a la de\ ref {4.28} en el límite como\(t \rightarrow \infty\).
5. Explicar cómo hacer para encontrar\(\mathrm{f}_{Y(t)}(y)\) en general, asumiendo que\(\mathrm{f}_{X}\) tiene una transformación racional de Laplace.

Ejercicio 4.38

Demostrar que para una cola G/G/1, el tiempo promedio de espera en el sistema es el mismo que\(\lim _{n \rightarrow \infty} \mathrm{E}\left[W_{n}\right]\). Pista: Considere un proceso de conteo de renovación de enteros\(\{M(n) ; n \geq 0\}\) donde\(M(n)\) está el número de renovaciones en el proceso G/G/1 de la Sección 4.5.3 que han ocurrido a la enésima llegada. Demostrar que este proceso de renovación tiene un lapso de 1. Entonces considera\(\left\{W_{n} ; n \geq 1\right\}\) como recompensa dentro de este proceso de renovación.

Ejercicio 4.39

Si se extiende la definición de procesos de renovación para incluir intervalos entre renovaciones de duración 0, con\(\operatorname{Pr}\{X=0\}=\alpha\), mostrar que el número esperado de renovaciones simultáneas en una época de renovación es\(1 /(1-\alpha)\), y que, para un proceso no aritmético, la probabilidad de 1 o más renovaciones en el intervalo\((t, t+\delta]\) tiende a\((1-\alpha) \delta / \mathrm{E}[X]+o(\delta)\) como\(t \rightarrow \infty\).

Ejercicio 4.40

El propósito de este ejercicio es mostrar por qué se justifica el intercambio de expectativa y suma en la prueba de la igualdad de Wald cuando\(\mathrm{E}[J]<\infty\) pero no de otra manera. Dejar\(X_{1}, X_{2}, \ldots\), ser una secuencia de IID rv, cada uno con la distribución\(\mathrm{F}_{X}\). Asumir eso\(\mathrm{E}[|X|]<\infty\).

1. Mostrar que\(S_{n}=X_{1}+\cdots+X_{n}\) es un rv para cada entero\(n>0\). Nota: obviamente\(S_{n}\) es un mapeo desde el espacio muestral a los números reales, pero debes demostrar que es finito con probabilidad 1. Pista: Recordemos el axioma de la aditividad para los números reales.
2. Deja\(J\) ser un juicio de detención para\(X_{1}, X_{2}, \ldots\) Show que\(S_{J}=X_{1}+\cdots X_{J}\) es un rv. Pista: Representar\(\operatorname{Pr}\left\{S_{J}\right\}\) como\(\sum_{n=1}^{\infty} \operatorname{Pr}\{J=n\} S_{n}\).
3. Para el juicio de detención\(J\) anterior, deja\(J^{(k)}=\min (J, k)\) ser el juicio de detención\(J\) truncado a entero\(k\). Explique por qué en este caso se justifica el intercambio de suma y expectativa en la prueba de la igualdad de Wald, así\(\mathrm{E}\left[S_{J^{(k)}}\right]=\overline{X} \mathrm{E}\left[J^{(k)}\right]\).
4. En las partes d), e), y f), supongamos, además de los supuestos anteriores, que, es decir, que\(\lim _{k \rightarrow \infty} \mathrm{E}\left[S_{J^{(k)}}\right]<\infty\) los\(X_{i}\) son rv positivos\(\mathrm{E}[J]=\infty\).\(\mathrm{F}_{X}(0)=0\)\(\mathrm{E}[J]<\infty\)\(\lim _{k \rightarrow \infty} \mathrm{E}\left[S_{J^{(k)}}\right]=\infty\)
5. Demostrar que

   \(\operatorname{Pr}\left\{S_{J^{(k)}}>x\right\} \leq \operatorname{Pr}\left\{S_{J}>x\right\}\)

   para todos\(k\),\(x\).

6. Demuestre eso\(\mathrm{E}\left[S_{J}\right]=\overline{X} \mathrm{E}[J]\) y\(\mathrm{E}\left[S_{J}\right]=\infty \text { if } \mathrm{E}[J]=\infty\).
7. Ahora supongamos que\(X\) tiene valores tanto negativos como positivos con probabilidad distinta de cero y let\(X^{+}=\max (0, X)\) y\(X^{-}=\min (X, 0)\). Expresar\(S_{J}\) como\(S_{J}^{+}+S_{J}^{-}\) dónde\(S_{J}^{+}=\sum_{i=1}^{J} X_{i}^{+}\) y\(S_{J}^{-}=\sum_{i=1}^{J} X_{i}^{-}\). Demostrar que\(\mathrm{E}\left[S_{J}\right]=\overline{X} \mathrm{E}[J]\) si\(\mathrm{E}[J]<\infty\) y eso\(\mathrm{E}\left[S_{j}\right]\) es indefinido de otra manera.

Ejercicio 4.41

Este es un ejercicio muy simple diseñado para aclarar la confusión sobre los roles del pasado, presente y futuro en detener las reglas. Dejar\(\left\{X_{n} ; n \geq 1\right\}\) ser una secuencia de rv binarios IID, cada uno con el pmf\(\mathrm{p}_{X}(1)=1/2, \mathrm{p}_{X}(0)=1/2\). Dejar\(J\) ser un rv con valor entero positivo que tome el valor muestral\(n\) del primer ensayo para el cual\(X_{n}=1\). Es decir, para cada uno\(n \geq 1\),

\(\{J=n\}=\left\{X_{1}=0, X_{2}=0, \ldots, X_{n-1}=0, X_{n}=1\right\}\)

1. Utilice la definición de detener el juicio, Definición 4.5.1 en el texto, para demostrar que\(J\) es un juicio de detención para\(\left\{X_{n} ; n \geq 1\right\}\).
2. Demostrar que para cualquier dado\(n\), los rv\(X_{n}\) y\(\mathbb{I}_{J=n}\) son estadísticamente dependientes.
3. Demostrar que para cada\(m>n\),\(X_{n}\) y\(\mathbb{I}_{J=m}\) son estadísticamente dependientes.
4. Demostrar que para cada\(m<n\),\(X_{n}\) y\(\mathbb{I}_{J=m}\) son estadísticamente independientes.
5. Demostrar eso\(X_{n}\) y\(\mathbb{I}_{J \geq n}\) son estadísticamente independientes. Da la caracterización más sencilla que puedas del evento\(\{J \geq n\}\).
6. Demostrar eso\(X_{n}\) y\(\mathbb{I}_{J>n}\) son estadísticamente dependientes.

Nota: Los resultados aquí son característicos de la mayoría de las secuencias de IID rv, para la mayoría de las personas, esto requiere un cierto realineamiento de la intuición, ya que\(\{J \geq n\}\) es la unión de\(\{J=m\}\) para todos\(m \geq n\), y todos estos eventos son altamente dependientes\(X_{n}\). La manera correcta de pensar en esto es que\(\{J \geq n\}\) es el complemento de\(\{J<n\}\), que está determinado por\(X_{1}, \ldots, X_{n-1}\). Así también\(\{J \geq n\}\) está determinado por\(X_{1}, \ldots, X_{n-1}\) y por lo tanto es independiente de\(X_{n}\). La moraleja de la historia es que pensar en detener las reglas como rv independientes del futuro es muy complicado, incluso en casos totalmente obvios como este.

Ejercicio 4.42

Supongamos que un amigo ha desarrollado un excelente programa para encontrar las probabilidades de estado estacionario para las cadenas de Markov de estado finito. Más precisamente, dada la matriz de transición\([\mathrm{P}]\), el programa regresa\(\lim _{n \rightarrow \infty} P_{i i}^{n}\) para cada uno\(i\). Supongamos que todas las cadenas son aperiódicas.

1. Se quiere encontrar el tiempo esperado para llegar primero a un estado determinado a\(k\) partir de un estado diferente\(m\) para una cadena de Markov con matriz de transición\([P]\). Se modifica la matriz a\(\left[P^{\prime}\right]\) donde\(P_{k m}^{\prime}=1, P_{k j}^{\prime}=0\) para\(j \neq m\), y de\(P_{i j}^{\prime}=P_{i j}\) otra manera. ¿Cómo encuentra el primer tiempo de paso deseado a partir de la salida del programa dada\(\left[P^{\prime}\right]\) como entrada? (Pista: Los tiempos en los que una cadena de Markov entra en un estado dado pueden considerarse como renovaciones en un proceso de renovación (quizás retrasado)).
2. Usando lo\(\left[P^{\prime}\right]\) mismo que la entrada del programa, ¿cómo se puede encontrar el número esperado de retornos al estado\(m\) antes del primer paso al estado\(k\)?
3. Supongamos que para la misma cadena de Markov\([P]\) y el mismo estado inicial\(m\), se quiere encontrar la probabilidad de llegar a algún estado dado\(n\) antes del primer paso a\(k\). Modifique\([P]\) a algunos para\(\left[P^{\prime \prime}\right]\) que el programa anterior con\(P^{\prime \prime}\) como entrada le permita encontrar fácilmente la probabilidad deseada.
4. \(\operatorname{Pr}\{X(0)=i\}=Q_{i}, 1 \leq i \leq \mathrm{M}\)Sea un conjunto arbitrario de probabilidades iniciales para la misma cadena de Markov\([P]\) que la anterior. Mostrar cómo modificar\([P]\) a algunos\(\left[P^{\prime \prime \prime}\right]\) para los cuales las probabilidades de estado estacionario permiten encontrar fácilmente el tiempo esperado del primer paso a estado\(k\).

Ejercicio 4.43

Considera un ferry que lleve autos a través de un río. El ferry tiene un número entero\(\k\) de automóviles y sale del muelle cuando está lleno. En ese momento, aparece inmediatamente un nuevo ferry y comienza a cargar autos recién llegados ad infinitum. El negocio del ferry ha sido bueno, pero los clientes se quejan de la larga espera para que se llene el ferry.

1. Supongamos que los autos llegan de acuerdo a un proceso de renovación. Los tiempos de interllegada del IID tienen media\(\overline{X}\), varianza\(\sigma^{2}\) y función generadora de momento\(g_{X}(r)\). ¿La secuencia de horarios de salida de los ferries forma un proceso de renovación? Explique cuidadosamente.
2. Encuentra el tiempo esperado que espera un cliente, a partir de su llegada a la terminal del ferry y terminando a la salida de su ferry. Nota 1: Parte del problema aquí es dar una definición razonable del tiempo de espera esperado del cliente. Nota 2: Podría ser útil considerar\(k=1\) y\(k=2\) primero.
3. ¿Existe un fenómeno de 'camión lento' (una dependencia de\(\mathrm{E}\left[X^{2}\right]\) aquí? Dar una explicación intuitiva. Pista: Mira\(k=1\) y\(k=2\) otra vez.
4. En un esfuerzo por disminuir la espera, los gestores del ferry instituyen una política donde ningún cliente tenga que esperar más de una hora. Así, el primer cliente en llegar después de la salida de un ferry espera ya sea una hora o la hora a la que el ferry está lleno, lo que ocurra primero, y luego el ferry sale y un nuevo ferry comienza a acumular nuevos clientes. ¿La secuencia de salidas de ferry forma un proceso de renovación bajo este nuevo sistema? ¿La secuencia de tiempos en que cada ferry vacío sucesivo es ingresado por su primer cliente forma un proceso de renovación? Se puede suponer aquí que\(t = 0\) es el momento de la primera llegada al primer ferry. Explique cuidadosamente.
5. Dar una expresión del tiempo de espera esperado del primer cliente nuevo en ingresar a un ferry vacío bajo esta nueva estrategia.