1.4: Desigualdades básicas

Las desigualdades juegan un papel particularmente fundamental en la probabilidad, en parte porque muchos de los modelos que estudiamos son demasiado complejos para encontrar respuestas exactas, y en parte porque muchos de los teoremas más útiles establecen resultados limitantes y no exactos. En esta sección, estudiamos tres desigualdades relacionadas, los límites de Markov, Chebyshev y Chernoff. Éstas se utilizan repetidamente tanto en la siguiente sección como en el resto del texto.

Desigualdad de Markov

Esta es la más simple y básica de estas desigualdades. Afirma que si una variable aleatoria no negativa$Y$ tiene una media$\mathrm{E}[Y]$, entonces, por cada$y>0$,$\operatorname{Pr}\{Y \geq y\}$ satisface ²⁷

$$\operatorname{Pr}\{Y \geq y\} \leq \frac{\mathrm{E}[Y]}{y} \quad \text { Markov Inequality for nonnegative } Y\label{1.54}$$

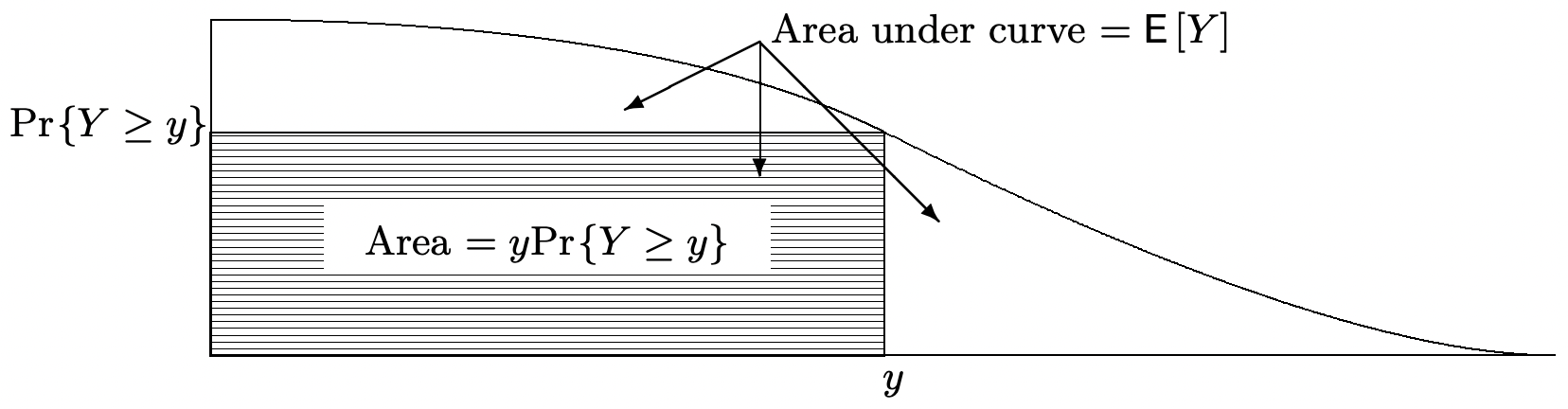
La Figura 1.7 deriva este resultado utilizando el hecho (ver Figura 1.3) de que la media de un rv no negativo es la integral de su función de distribución complementaria, es decir, del área bajo la curva$\operatorname{Pr}\{Y>z\}$. El ejercicio 1.28 da otra prueba simple usando una variable aleatoria indicadora.

Como ejemplo de esta desigualdad, supongamos que la estatura promedio de una población de personas es de 1.6 metros. Entonces la desigualdad de Markov afirma que a lo sumo la mitad de la población tiene una altura superior a 3.2 metros. Vemos de este ejemplo que la desigualdad de Markov suele ser muy débil. Sin embargo, para cualquiera$y>0$, podemos considerar una rv que tome el valor$y$ con probabilidad$\epsilon$ y el valor 0 con probabilidad$1-\epsilon$; esta rv satisface la desigualdad de Markov en el punto$y$ con igualdad. La Figura 1.7 (como se elabora en el Ejercicio 1.40) también muestra que, para cualquier rv Y no negativo con una media finita,

$$\lim _{y \rightarrow \infty} y \operatorname{Pr}\{Y \geq y\}=0\label{1.55}$$

Esto será útil en breve en la prueba del Teorema 1.5.3.

Figura 1.7: Demostración de que$y \operatorname{Pr}\{Y \geq y\} \leq \mathrm{E}[Y]$. Al dejar$y \rightarrow \infty$, también se puede ver que el área sombreada se convierte en una porción insignificante del área$\mathrm{E}[Y]$, de manera que$\lim _{y \rightarrow \infty} y \operatorname{Pr}\{Y>y\}=0 \text { if } \mathrm{E}[Y]<\infty$

Desigualdad de Chebyshev

Ahora utilizamos la desigualdad de Markov para establecer la conocida desigualdad de Chebyshev. Dejar$Z$ ser un rv arbitrario con media finita$\mathrm{E}[Z]$ y varianza finita$\sigma_{Z}^{2}$, y definir$Y$ como el rv no negativo$Y=(Z-\mathrm{E}[Z])^{2}$. Así$\mathrm{E}[Y]=\sigma_{Z}^{2}$. Aplicando (1.54),

$\operatorname{Pr}\left\{(Z-\mathrm{E}[Z])^{2} \geq y \leq \frac{\sigma_{Z}^{2}}{y} \quad \text { for any } y>0\right.$

Reemplazar y por$\epsilon^{2}$ (para cualquier$\epsilon>0$) y señalando que el evento$\left\{(Z-\mathrm{E}[Z])^{2} \geq \epsilon^{2}\right\}$ es el mismo que$|Z-\mathrm{E}[Z]| \geq \epsilon$, esto se convierte

$$\operatorname{Pr}\{|Z-\mathrm{E}[Z]| \geq \epsilon\} \leq \frac{\sigma_{Z}^{2}}{\epsilon^{2}} \quad(\text { Chebyshev inequality })\label{1.56}$$

Tenga en cuenta que la desigualdad de Markov limita solo la cola superior de la función de distribución y se aplica solo a los rv no negativos, mientras que la desigualdad de Chebyshev limita ambas colas de la función de distribución. La diferencia más importante, sin embargo, es que el límite de Chebyshev va a cero inversamente con el cuadrado de la distancia desde la media, mientras que el límite de Markov va a cero inversamente con la distancia desde 0 (y así asintóticamente con la distancia desde la media).

La desigualdad de Chebyshev es particularmente útil cuando$Z$ es el promedio muestral$\left(X_{1}+X_{2}+\dots X_n\right.)/n$,, de un conjunto de IID rv, que se utilizará en breve para probar la débil ley de grandes números.

Límite de Chernoff

Los límites de Chernoff (o exponenciales) son otra variación de la desigualdad de Markov en la que el límite en cada cola de la función de distribución va a 0 exponencialmente con la distancia desde la media. Para cualquier rv dado$Z$, deja$I(Z)$ ser el intervalo sobre el cual$\left.\operatorname{MGF} g_{Z}(r)=\mathrm{E}\left[e^{Z r}\right]\right\}$ existe el. Dejando$Y=e^{Z r}$ para cualquiera$r \in I(Z)$, la desigualdad de Markov\ ref {1.54} aplicada a$Y$ es

$\operatorname{Pr}\{\exp (r Z) \geq y\} \leq \frac{\mathrm{g}_{Z}(r)}{y} \quad \text { for any } y>0$

Esto adquiere una forma más significativa si$y$ es reemplazado por$e^{r b}$. Tenga en cuenta que exp$(r Z) \geq \exp (r b)$ es equivalente a$Z \geq b$ for$r>0$ y to$Z<b$ for$r<0$. Así, para cualquier real$b$, obtenemos los siguientes dos límites, uno para$r>0$ y otro para$r<0$:

$$\operatorname{Pr}\{Z \geq b\} \leq g_{Z}(r) \exp (-r b) ; \quad \text { (Chernoff bound for } 0<r \in I(Z)\label{1.57}$$

$$\left.\operatorname{Pr}\{Z \leq b\} \leq g_{Z}(r) \exp (-r b) ; \quad \text { (Chernoff bound for } 0>r \in I(Z)\right)\label{1.58}$$

Esto nos proporciona una familia de límites superiores en las colas de la función de distribución, utilizando valores de$r>0$ para la cola superior y$r<0$ para la cola inferior. Para fijo$0<r \in I(Z)$, este límite en$\operatorname{Pr}\{Z \geq b\}$ disminuye exponencialmente ²⁸ in$b$ a tasa$r$. De igual manera, para cada uno$0>r \in I(Z)$, el límite en$\operatorname{Pr}\{Z \leq b\}$ disminuye exponencialmente a la velocidad$r$ como$b \rightarrow-\infty$. Veremos en breve que\ ref {1.57} es útil solo cuando$b>\mathrm{E}[X]$ y\ ref {1.58} es útil solo cuando$b<\mathrm{E}[X])$.

La aplicación más importante de estos límites de Chernoff es a sumas de IID rv. Vamos$S_{n}=X_{1}+\cdots+X_{n}$ donde$X_{1}, \ldots, X_{n}$ están IID con el MGF$\mathrm{g}_{X}(r)$. Entonces$\mathrm{g}_{S_{n}}(r)=\left[\mathrm{g}_{X}(r)\right]^{n}$, así que\ ref {1.57} y\ ref {1.58} (con$b$ reemplazado por$na$) se convierten

$$\operatorname{Pr}\left\{S_{n} \geq n a\right\} \leq\left[\mathrm{g}_{X}(r)\right]^{n} \exp (-r n a) ; \quad(\text { for } 0<r \in I(Z))\label{1.59}$$

$$\operatorname{Pr}\left\{S_{n} \leq n a\right\} \leq\left[\mathrm{g}_{X}(r)\right]^{n} \exp (-r n a) ; \quad(\text { for } 0>r \in I(Z))\label{1.60}$$

Estas ecuaciones son más fáciles de entender si definimos el MGF semiinvariante,$\gamma_{X}(r)$, como

$$\gamma_{X}(r)=\ln g_{X}(r)\label{1.61}$$

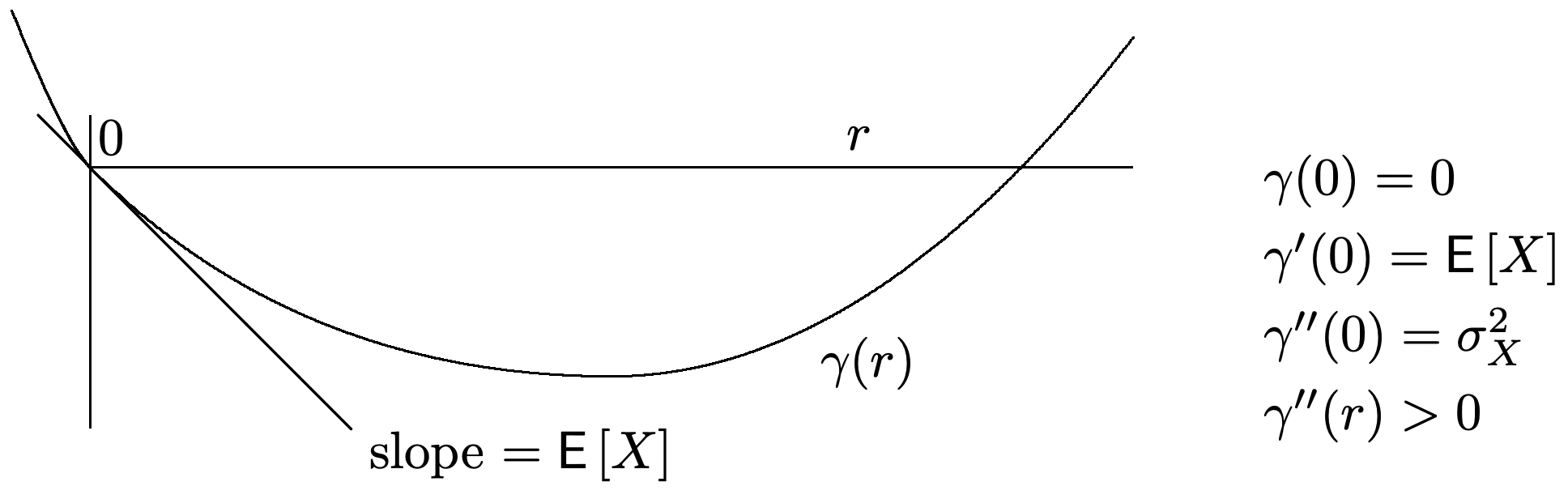
El MGF semiinvariante para un rv típico$X$ se esboza en la Figura 1.8. Las principales características a observar son, primero, eso$\gamma_{X}^{\prime}(0)=\mathrm{E}[X]$ y, segundo, que$\gamma_{X}^{\prime \prime}(r) \geq 0$ para$r$ en el interior de$I(X)$..

Figura 1.8: Función semi-invariante de generación de momentos$\gamma(r)$ para un rv típico$X$ asumiendo$r_{-}<0<r_{+}$. Ya que$\gamma(r)=\ln g(r)$, vemos que eso$\frac{\partial}{\partial r} \gamma(r)=\frac{1}{g(r)} \frac{\partial}{\partial r} g(r)$. Así$\gamma^{\prime}(0)=\mathrm{E}[X]$. También, pues$r$ en el interior de$I(X)$, el Ejercicio 1.24 muestra que$\gamma^{\prime \prime}(r) \geq 0$, y de hecho,$\gamma^{\prime \prime}(r)$ es estrictamente positivo salvo en el caso poco interesante donde$X$ es determinista (adquiere un solo valor con probabilidad 1). Como se indica en la figura, la línea recta de pendiente$\mathrm{E}[X]$ a través del origen es tangente a$\gamma(r)$.

En términos de$\gamma_{X}(r)$,\ ref {1.59} y\ ref {1.60} convertirse

$$\operatorname{Pr}\left\{S_{n} \geq n a\right\} \leq \exp \left(n\left[\gamma_{X}(r)-r a\right]\right) ; \quad(\text { for } 0<r \in I(X)\label{1.62}$$

$$\operatorname{Pr}\left\{S_{n} \leq n a\right\} \leq \exp \left(n\left[\gamma_{X}(r)-r a\right]\right) ; \quad(\text { for } 0>r \in I(X)\label{1.63}$$

Estos límites son geométricos en$n$ para fijos$a$ y$r$, por lo que debemos preguntar qué valor de$r$ proporciona el límite más ajustado para cualquier dado$a$. Ya que$\gamma_{X}^{\prime \prime}(r)>0$, el límite más apretado surge ya sea en aquello$r$ para el cual$\gamma^{\prime}(r)=a$ o en uno de los puntos finales,$r_{-}$ o$r_{+}$, de$I(X)$. Este valor mínimo se denota por

$\mu_{X}(a)=\inf _{r}\left[\gamma_{X}(r)-r a\right]$

Tenga en cuenta que$\left.\left(\gamma_{X}(r)-r a\right)\right|_{r=0}=0$ y$\left.\frac{\partial}{\partial r}\left(\gamma_{X}(r)-r a\right)\right|_{r=0}=\mathrm{E}[X]-a$. Por lo tanto si$a>E[X]$, entonces$\gamma_{X}(r)-r a$ debe ser negativo para el positivo suciamente pequeño$r$. De igual manera$a<\mathrm{E}[X]$, si, entonces$\gamma_{X}(r)-r a$ es negativo para negativo$r$ sucientemente cerrar ²⁹ a 0. En otras palabras,

$$\operatorname{Pr}\left\{S_{n} \geq n a\right\} \leq \exp \left(n \mu_{X}(a)\right) ; \quad \text { where } \mu_{X}(a)<0 \text { for } a>\mathrm{E}[X]\label{1.64}$$

$$\operatorname{Pr}\left\{S_{n} \leq n a\right\} \leq \exp \left(n \mu_{X}(a)\right) ; \quad \text { where } \mu_{X}(a)<0 \text { for } a<\mathrm{E}[X]\label{1.65}$$

Esto se resume en el siguiente lema:

Lema 1.4.1. Supongamos que 0 está en el interior de$I(X)$ y deja$S_{n}$ ser la suma de$n$ IID rv cada uno con la distribución de$X$. Entonces$\mu_{X}(a)=\inf _{r}\left[\gamma_{X}(r)-r a\right]<0$ para todos$a \neq \mathrm{E}[X]$. También,$\operatorname{Pr}\left\{S_{n} \geq n a\right\} \leq e^{n \mu_{X}(a)}$ para$a>E[X]$ y$\operatorname{Pr}\left\{S_{n} \leq n a\right\} \leq e^{n \mu_{X}(a)}$ para$a<\mathrm{E}[X]$.

La Figura 1.9 ilustra el lema y da una construcción gráfica para encontrar ³⁰$\mu_{X}(a)=\mathrm{inf}_r[\gamma_X(r)-ra]$.

Estos límites de Chernoff serán utilizados en la siguiente sección para ayudar a entender varias leyes de grandes números. También se utilizarán ampliamente en el Capítulo 7 y son útiles para la detección, caminatas aleatorias y teoría de la información.

El siguiente ejemplo evalúa estos límites para el caso en el que los IID rv son binarios. Veremos que en este caso los límites son exponencialmente apretados en un sentido a describir.

Ejemplo 1.4.1. Dejar$X$ ser binario con$\mathrm{p}_{X}(1)=p$ y$\mathrm{p}_{X}(0)=q=1-p$. Entonces$g_{X}(r)=q+pe^r$ para$-\infty<r<\infty$. También,$\gamma_{X}(r)=\ln \left(q+p e^{r}\right)$. Para ser consistentes con la expresión del binomio PMF en (1.23), encontraremos límites a$\operatorname{Pr}\left\{S_{n} \geq \tilde{p} n\right\}$ y$\operatorname{Pr}\left\{S_{n} \leq \tilde{p} n\right\}$ para$\tilde{p}>p$ y$\tilde{p}<p$ respectivamente. Así, de acuerdo con Lemma 1.4.1, primero evaluamos

$\mu_{X}(\tilde{p})=\inf _{r}\left[\gamma_{X}(r)-\tilde{p} r\right]$

El mínimo ocurre en aquel$r$ para el cual$\gamma_{X}^{\prime}(r)=\tilde{p}$, es decir, en

$\frac{p e^{r}}{q+p e^{r}}=\tilde{p}$

Figura 1.9: Minimización gráfica de$\gamma(r)-a r$: Para cualquiera$r \in I(X), \gamma(r)-a r$ es la intercepción del eje vertical de una línea de pendiente$a$ a través del punto$(r, \gamma(r))$. El mínimo ocurre cuando la línea de pendiente$a$ es tangente a la curva. Los dos ejemplos muestran un caso donde$\mathrm{E}[X]<0$ y otro donde$\mathrm{E}[X]>0$.

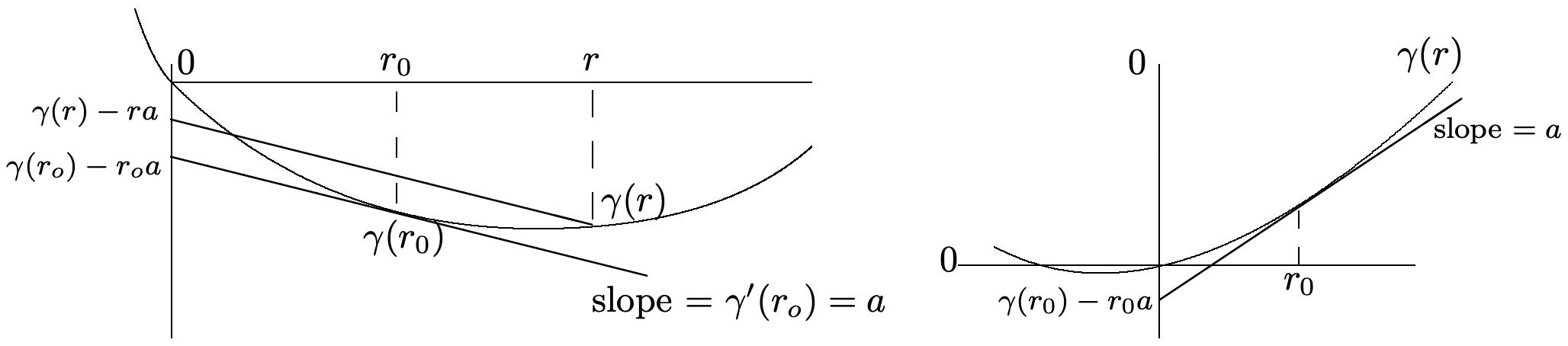
Reorganización de términos,

$$e^{r}=\frac{\tilde{p} q}{p \tilde{q}} \quad \text { where } \tilde{q}=1-\tilde{p} .\label{1.66}$$

Sustituyendo este valor minimizado de$r$ en términos$\ln \left(q+p e^{r}\right)-r \tilde{p}$ y reordenándolos,

$$\mu_{X}(\tilde{p})=\tilde{p} \ln \frac{p}{\tilde{p}}+\tilde{q} \ln \frac{\tilde{q}}{q}\label{1.67}$$

Sustituyendo esto en (1.64), y (1.65), obtenemos los siguientes límites de Chernoff para IID binarios rv Como se muestra arriba, están disminuyendo exponencialmente en$n$.

$$\left.\operatorname{Pr}\left\{S_{n} \geq n \tilde{p}\right\} \leq \exp \left\{n\left[\tilde{p} \ln \frac{p}{\tilde{p}}+\tilde{q} \ln \frac{q}{\tilde{q}}\right]\right\}\right\} ; \quad \text { for } \tilde{p}>p\label{1.68}$$

$$\left.\operatorname{Pr}\left\{S_{n} \leq n \tilde{p}\right\} \leq \exp \left\{n\left[\tilde{p} \ln \frac{p}{\tilde{p}}+\tilde{q} \ln \frac{q}{\tilde{q}}\right]\right\}\right\} ; \quad \text { for } \tilde{p}<p\label{1.69}$$

Hasta el momento, parece que simplemente hemos desarrollado otro límite superior en las colas de la función de distribución para el binomio. Entonces tal vez sea sorprendente comparar esta unión con el valor asintóticamente correcto (repetido a continuación) para el PMF binomial en (1.26).

$$\mathrm{p}_{S_{n}}(k) \sim \sqrt{\frac{\}1}{2 \pi n \tilde{p} \tilde{q}}} \exp n[\tilde{p} \ln (p / \tilde{p})+\tilde{q} \ln (q / \tilde{q})] \quad \text { for } \tilde{p}=\frac{k}{n}\label{1.70}$$

Para cualquier valor entero de$n \tilde{p}$ con$\tilde{p}>p$, podemos reducir el límite$\operatorname{Pr}\left\{S_{n} \geq n \tilde{p}\right\}$ por el término único$\mathrm{p}_{S_{n}}(n \tilde{p})$. Así$\operatorname{Pr}\left\{S_{n} \geq n \tilde{p}\right\}$, tanto superior como inferior están delimitados por cantidades que disminuyen exponencialmente con$n$ la misma tasa. El límite inferior es asintótico$n$ y tiene el coeciente$1 / \sqrt{2 \pi n \tilde{p} \tilde{q}}$. Estas diferencias son esencialmente insignificantes para grandes$n$ en comparación con el término exponencial. Podemos expresarlo analíticamente considerando el log del límite superior en\ ref {1.68} y el límite inferior en (1.70).

$$\left.\lim _{n \rightarrow \infty} \frac{\ln \operatorname{Pr}\left\{S_{n} \geq n \tilde{p}\right\}}{n}=\left[\tilde{p} \ln \frac{p}{\tilde{p}}+\tilde{q} \ln \frac{q}{\tilde{q}}\right]\right\} \quad \text { where } \tilde{p}>p\label{1.71}$$

---

Referencia

²⁷ La función de distribución de cualquier rv dada$Y$ es conocida (al menos en principio), y así uno podría preguntarse por qué un límite superior es siempre preferible al valor exacto. Una respuesta es que$Y$ podría darse en función de muchos otros rv y que los parámetros como la media en un límite son mucho más fáciles de encontrar que la función de distribución. Otra respuesta es que tales desigualdades se utilizan a menudo en teoremas que indican los resultados en términos de estadísticas simples como la media y no toda la función de distribución. Esto será evidente a medida que usemos estos límites.

²⁸ Esto parece paradójico, ya que$Z$ parece ser casi arbitrario. Sin embargo, ya que$r \in I(Z)$, tenemos$\int e^{r b} d \mathrm{~F}_{Z}(b)<\infty$.

²⁹ De hecho, para r suciamente pequeño,$\gamma(r)$ puede ser aproximado por una serie de potencia de segundo orden,$\gamma(r)\approx\gamma(0)+r \gamma^{\prime}(0)+\left(r^{2} / 2\right) \gamma^{\prime \prime}(0)=r \bar{X}+\left(r^{2} / 2\right) \sigma_{X}^{2}$. De ello se deduce que$\mu_{X}(a) \approx-(a-\bar{X})^{2} / 2 \sigma_{X}^{2}$ para muy pequeños$r$.

³⁰ Como caso especial, el infimum podría ocurrir en el borde del intervalo de convergencia, es decir, en$r_{-}$ o$r_{+}$. Como se muestra en el Ejercicio 1.23, el infimum puede estar en$r_{+}\left(r_{-}\right)$ solo si$g_{X}\left(r_{+}\right)\left(g_{X}\left(r_{-}\right)\right.$ existe, y en este caso, la tecinique gráfica en la Figura 1.9 aún funciona.