10.6: Filtros Anti-Aliasing
- Page ID
- 86455
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introducción
Se ha demostrado que una señal de\((−B,B)\) banda limitada puede ser perfectamente reconstruida a partir de sus muestras a una velocidad\(\omega_s=2 \pi /T_s≥B\). Sin embargo, no siempre es prácticamente posible producir frecuencias de muestreo suficientemente altas o asegurar que la entrada esté limitada en banda en situaciones reales. El aliasing, que se manifiesta como una diferencia de forma entre los periodos del espectro de señal de muestras y el espectro original, ocurriría sin ninguna medida adicional para corregirlo. Por lo tanto, a menudo se hace necesario filtrar la energía de la señal a frecuencias superiores\(\omega_s/2\) para evitar los efectos perjudiciales del aliasing. Este es el papel del filtro anti-aliasing, un filtro de paso bajo aplicado antes del muestreo para asegurar que la señal esté\((−\omega_s/2, \omega_s/2)\) limitada en banda o al menos casi así.
Filtros antialiasing
El aliasing puede ocurrir cuando una señal con energía en otras frecuencias que\((−B,B)\) se muestrea a velocidad\(\omega_s<2B\). Así, cuando se muestrea por debajo de la frecuencia Nyquist, es deseable eliminar la mayor cantidad posible de energía de señal fuera del rango de frecuencia mientras\((−B,B)\) se mantiene la mayor cantidad de energía de señal en el rango de frecuencia\((−B,B)\) como sea posible. Esto sugiere que el filtro de paso bajo ideal con frecuencia de corte\(\omega_s/2\) sería el filtro antialiasing óptimo para aplicar antes del muestreo. Si bien esto es cierto, el filtro de paso bajo ideal solo se puede aproximar en situaciones reales.
Para demostrar la importancia de los filtros anti-aliasing, considere el cálculo de la energía de error entre la señal original y su reconstrucción Whittaker-Shannon a partir de sus muestras tomadas con y sin el uso de un filtro anti-aliasing. Dejar\(x\) ser la señal original y\(y=Gx\) ser la señal filtrada anti-alias donde\(G\) está el filtro de paso bajo ideal con frecuencia de corte\(\omega_s/2\). Es fácil demostrar que el espectro reconstruido sin filtro anti-aliasing viene dado por
\ [\ Widetilde {X} (\ omega) =\ left\ {\ begin {array} {cl}
T_ {s} X_ {s}\ left (T_ {s}\ omega\ right) & |\ omega|<\ omega_ {s}/2\\
0 &\ text {de lo contrario}
\ end {array} =\ left\ {\ begin {array} {cc}
\ sum_ {k=-\ infty} ^ {\ infty} X\ izquierda (\ omega-k\ omega_ {s}\ derecha) & | \ omega|<\ omega_ {s}/2\\
0 &\ text {de lo contrario}
\ end {array}\ right. \ derecho. \ nonumber\]
Así, el espectro de error de reconstrucción para este caso es
\ [(X-\ Widetilde {X}) (\ omega) =\ izquierda\ {\ comenzar {array} {cc}
-\ sum_ {k=1} ^ {\ infty}\ izquierda (X\ izquierda (\ omega+k\ omega_ {s}\ derecha) +X\ izquierda (\ omega-k\ omega_ {s}\ derecha)\ derecha) & |\ omega<\ omega_ {s}/2\\
X (\ omega) &\ text {de lo contrario}
\ end {array}\ right.. \ nonumber\]
De manera similar, el espectro reconstruido usando el filtro anti-aliasing de paso bajo ideal viene dado por
\ [\ Widetilde {Y} (\ omega) =Y (\ omega) =\ left\ {\ begin {array} {cc}
X (\ omega) & |\ omega|<\ omega_ {s}/2\\
0 &\ text {de lo contrario}
\ end {array}\ derecha.. \ nonumber\]
Así, el espectro de error de reconstrucción para este caso es
\ [(X-\ Widetilde {Y}) (\ omega) =\ left\ {\ begin {array} {cc}
0 & |\ omega|<\ omega_ {s}/2\\
X (\ omega) &\ text {de lo contrario}
\ end {array}\ right. \ nonumber\]
De ahí que, por el teorema de Parseval, se deduce que\(\|x-\tilde{y}\| \leq\|x-\tilde{x}\|\). También tenga en cuenta que el espectro de\(\widetilde{Y}\) es idéntico al de la señal original\(X\) en frecuencias\(\omega \in\left(-\omega_{s} / 2, \omega_{s} / 2\right)\). Esto se muestra gráficamente en la Figura\(\PageIndex{1}\).
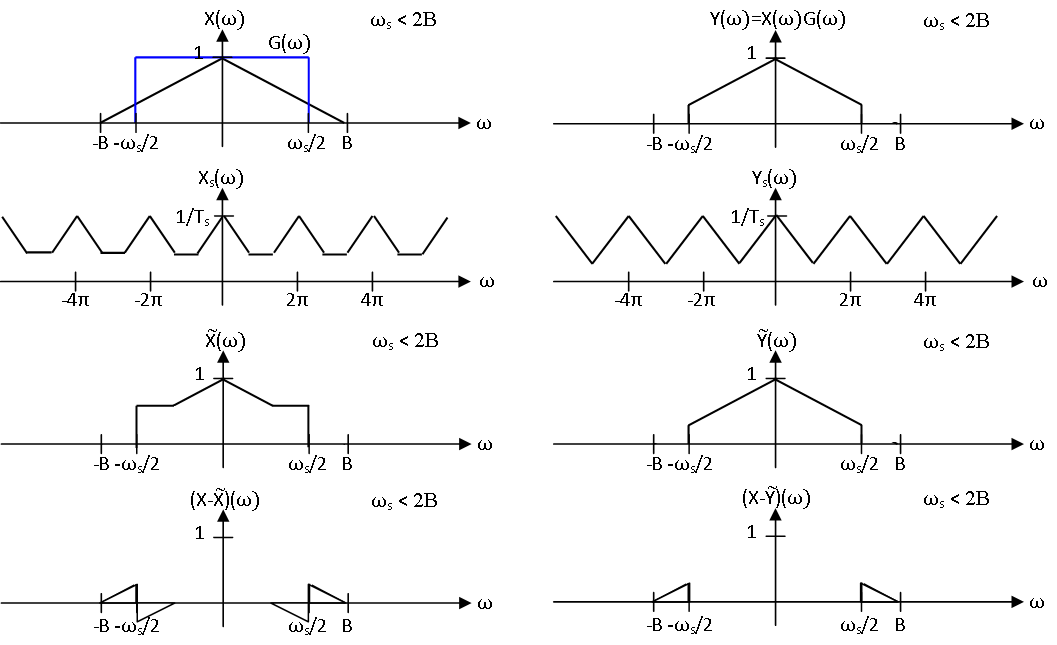
Resumen de filtros antialiasing
Como se puede ver, los filtros anti-aliasing aseguran que la señal esté\((−\omega_s/2,\omega_s/2)\) limitada en banda, o al menos casi así. El filtro antialiasing óptimo sería el filtro de paso bajo ideal con frecuencia de corte at\(\omega_s/2\), lo que garantizaría que el espectro de señal original y el espectro de señal reconstruido sean iguales en el intervalo\((−\omega_s/2,\omega_s/2)\). Sin embargo, el filtro de paso bajo ideal no es posible implementar en la práctica, y en su lugar deben aceptarse aproximaciones. Los filtros antialiasing son un componente importante de los sistemas que implementan el procesamiento de tiempo discreto de señales de tiempo continuas, como se mostrará en el módulo posterior.


