1.6: Problemas
- Page ID
- 86779
Sección 1-1
1. Encuentra el área de un círculo en el\(xy\) plano centrado en el origen usando:
(a) coordenadas rectangulares\(x + y^{2} = a^{2}\) (Pista:
\(\int \sqrt{a^{2} - x^{2}} dz = \frac{1}{2} [x \sqrt{a^{2} - x^{2}} + a^{2} \sin^{-1} (x /a)]\))
b) coordenadas cilíndricas\(\textrm{r}=a\).
¿Qué sistema de coordenadas es más fácil de usar?
2. Encuentra el volumen de una esfera de radio\(R\) centrada en el origen usando:
(a) coordenadas rectangulares\(x^{2} + y + z^{2} = R^{2}\) (Pista:
\(\int \sqrt{a^{2}-x^{2}}dx=\frac{1}{2}\left [x\sqrt{a^{2}-x^{2}}+a^{2}\sin ^{-1}\left ( x/a \right ) \right ]\))
b) coordenadas cilíndricas\(r^{2} + z^{2} = R^{2}\);
(c) coordenadas esféricas\(r=\textbf{R}\)
¿Qué sistema de coordenadas es el más sencillo?
Sección 1-2
Dados los tres vectores
\(\textbf{A} = 3 \textbf{i}_{x} + 2 \textbf{i}_{y} - \textbf{i}_{z} \\ \textbf{B} = 3 \textbf{i}_{x} - 4 \textbf{i}_{y} - 5 \textbf{i}_{z} \\ \textbf{C} = \textbf{i}_{x} - \textbf{i}_{y} + \textbf{i}_{z}\)
encuentra lo siguiente:
a)\(\textbf{A}\pm \textbf{B},\textbf{B}\pm \textbf{C},\textbf{A}\pm \textbf{C}\)
b)\(\textbf{A}\cdot \textbf{B},\textbf{B}\cdot \textbf{C},\textbf{A}\cdot \textbf{C}\)
c)\(\textbf{A}\times \textbf{B},\textbf{B}\times \textbf{C},\textbf{A}\times \textbf{C}\)
d)\(\left (\textbf{A}\times \textbf{B} \right )\cdot \textbf{C},\textbf{A}\cdot \left (\textbf{B}\times \textbf{C} \right )\) [¿Son iguales?]
e)\(\textbf{A}\times \left (\textbf{B} \times \textbf{C} \right ),\textbf{B}\left ( \textbf{A}\cdot \textbf{C} \right )-\textbf{C}\left ( \textbf{A}\cdot \textbf{B} \right )\) [¿Son iguales?]
f) ¿Cuál es el ángulo entre\(\textbf{A}\) y\(\textbf{C}\) y entre\(\textbf{B}\) y\(\textbf{A}\times\textbf{C}\)?
Dada la suma y diferencia entre dos vectores,
\(\textbf{A} + \textbf{B} = -\textbf{i}_{x} + 5 \textbf{i}_{y} - 4 \textbf{i}_{z} \\ \textbf{A} - \textbf{B} = 3 \textbf{i}_{x} - \textbf{i}_{y} - 2 \textbf{i}_{z}\)
encontrar los vectores individuales\(\textbf{A}\) y\(\textbf{B}\).
(a) Dados dos vectores \(\textbf{A}\)y\(\textbf{B}\), muestran que el componente de\(\textbf{B}\) paralelo a\(\textbf{A}\) es
\(\textbf{B}_{\parallel} = \frac{\textbf{B} \cdot \textbf{A}}{\textbf{A} \cdot \textbf{A}} \textbf{A}\)
(Pista:\(\textbf{B}_{\parallel} = \alpha \textbf{A}\). ¿Qué es\(\alpha\)?)
b) si los vectores son
\ (\ textbf {A} =\ textbf {i} _ {x} -2\ textbf {i} _ {y} +\ textbf {i} _ {z}\
\ textbf {B} =3\ textbf {i} _ {x} -5\ textbf {i} _ {y} -5\ textbf {i} _ {z}\)
¿Cuáles son los componentes de\(\textbf{B}\) paralelo y perpendicular a\(\textbf{A}\)?
\(\textbf{B} = \textbf{B}_{\perp} + \textbf{B}_{\parallel}\)
Cuáles son los ángulos entre cada uno de los siguientes vectores:
\(\textbf{A} = 4 \textbf{i}_{x} - 2 \textbf{i}_{y} + 2 \textbf{i}_{z} \\ \textbf{B} = -6 \textbf{i}_{x} + 3 \textbf{i}_{y} - 3 \textbf{i}_{z} \\ \textbf{C} = \textbf{i}_{x} + 3 \textbf{i}_{y} + \textbf{i}_{z}\)
Dados los dos vectores
\(\textbf{A} = 3 \textbf{i}_{x} + 4 \textbf{i}_{y} \textrm{ and } \textbf{B} = 7 \textbf{i}_{x} - 24 \textbf{i}_{y}\)
(a) ¿Cuál es su producto punto?
b) ¿Cuál es su producto cruzado?
c) ¿Cuál es el ángulo\(\theta\) entre los dos vectores?
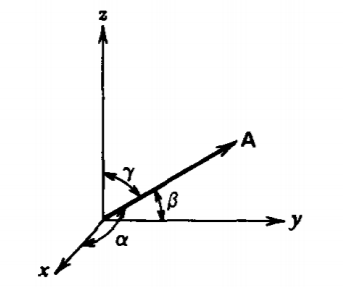
Dado el vector
\(\textbf{A} = \textbf{A}_{x}\textbf{i}_{x} + A_{y}\textbf{i}_{y} + A_{z}\textbf{i}_{z}\)
los cosenos direccionales se definen como los cosenos de los ángulos entre\(\) y cada uno de los ejes de coordenadas cartesianas. Encuentra cada uno de estos cosenos direccionales y demuestra que
\(\cos^{2} \alpha + \cos^{2} \beta + \cos^{2} \gamma = 1\)
Un triángulo está formado por los tres vectores\(\textbf{A}\),\(\textbf{B}\), y\(\textbf{C}=\textbf{B}-\textbf{A}\).
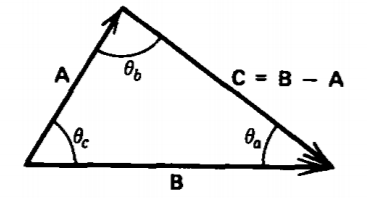
(a) Encontrar la longitud del vector\(\textbf{C}\) en términos de las longitudes de\(\textbf{A}\) y \(\textbf{B}\)y el ángulo cerrado\(\theta_{c}\). El resultado se conoce como la ley de los cosenos. (Pista:\(\textbf{C}\cdot \textbf{C}=\left ( \textbf{B}-\textbf{A} \right )\cdot \left ( \textbf{B}-\textbf{A} \right )\).)
b) Para el mismo triángulo, probar la ley de los senos:
\(\frac{\sin \: \theta_{a}}{A} = \frac{\sin \: \theta_{b}}{B} = \frac{\sin \: \theta_{c}}{C}\)
(Pista:\(\textbf{B}\times \textbf{A}=\left ( \textbf{C}+\textbf{A} \right )\times \textbf{A}\).)
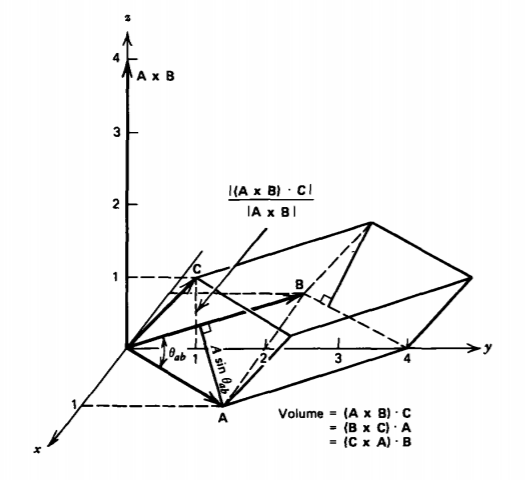
(a) Demostrar que el punto y la cruz pueden intercambiarse en el producto triple escalar
\(\left (\textbf{A}\times \textbf{B} \right )\cdot \textbf{C}=\left ( \textbf{B}\times \textbf{C} \right )\cdot \textbf{A}=\left ( \textbf{C}\times \textbf{A}\right )\cdot \textbf{B}\)
(b) Demostrar que este producto da el volumen de un paralelepípedo cuya base está definida por los vectores\(\)\(\) y cuya altura viene dada por\(\).
c) Si
\(\textbf{A} = \textbf{i}_{x} + 2 \textbf{i}_{y}, \: \: \: \textbf{B} = - \textbf{i}_{x} + 2 \textbf{i}_{y}, \: \: \: \textbf{C} = \textbf{i}_{x} + \textbf{i}_{z}\)
verificar las identidades de (a) y encontrar el volumen del paralelepípedo formado por los vectores.
(d) Demostrar la identidad del producto triple vector
\(\textbf{A}\times \left (\textbf{B}\times \textbf{C} \right )=\textbf{B}\left (\textbf{A}\cdot \textbf{C} \right )-\textbf{C}\left (\textbf{A}\cdot \textbf{B} \right )\)
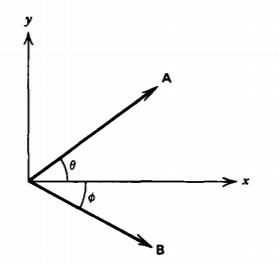
(a) Escribir los vectores\(\textbf{A}\) y\(\textbf{B}\) usar coordenadas cartesianas en términos de sus ángulos\(\theta\) y\(\phi\) desde el \(x\)eje.
b) Utilizando los resultados de (a) derivar las expansiones trigonométricas
\(\sin(\theta + \phi) = \sin \: \theta \: \cos \: \phi + \sin \: \phi \: \cos \: \theta\)
\(\cos (\theta + \phi) = \cos \: \theta \: \cos \: \phi - \sin \: \theta \: \sin \: \phi\)
Sección 1-3
Encuentra el gradiente de cada una de las siguientes funciones donde \(a\)y\(b\) son constantes:
a)\(f = axz + bx^{3}y\)
b)\(f = (a/\textrm{r}) \: \sin \: \phi + b \textrm{r} z^{2} \: \cos \: 3 \phi\)
c)\(f = ar \: \cos \: \theta + (b/r^{2}) \: \sin \: \phi\)
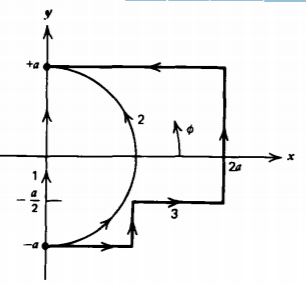
Evaluar la integral de línea del gradiente de la función
\(f = r \: \sin \: \phi\)
sobre cada uno de los contornos mostrados.
Sección 1-4
Encuentra la divergencia de los siguientes vectores:
a)\(\textbf{A} = x \textbf{i}_{x} + y \textbf{i}_{y} + z \textbf{i}_{z} = r \textbf{i}_{r}\)
b)\(\textbf{A} = (xy^{2}z^{3})[\textbf{i}_{x} + \textbf{i}_{y} + \textbf{i}_{z}]\)
c)\(\textbf{A} = \textrm{r} \: \cos \: \phi \textbf{i}_{\textrm{r}} + [(z/\textrm{r}) \: \sin \: \phi)] \textbf{i}_{z}\)
d)\(\textbf{A} = r^{2} \: \sin \: \theta \: \cos \: \phi \: [\textbf{i}_{r} + \textbf{i}_{\theta} + \textbf{i}_{\phi}]\)
Utilizando el teorema de divergencia probar las siguientes identidades integrales:
a)\(int_{V} \nabla f d V = \oint_{S} f \: \textbf{dS}\)
(Pista: Let\(\textbf{A}=\textbf{i}f\), donde\(\textbf{i}\) está cualquier vector de unidad constante.)
b)\(\int_{V} \nabla \times \textbf{F} \: d \textrm{V} = -\oint_{S} \textbf{F} \times \textbf{dS}\)
(Pista: Vamos\(\textbf{A}=\textbf{i}\times \textbf{F}\).)
c) Utilizando los resultados de (a) mostrar que el vector normal integrado sobre una superficie es cero:
\(\oint_{S} \textbf{dS} = 0\)
d) Verificar (c) para el caso de una esfera de radio\(R\).
(Pista:\(\textbf{i}_{r} = \sin \: \theta \: \cos \: \phi \textbf{i}_{x} + \sin \: \theta \: \sin \: \phi \textbf{i}_{y} + \cos \: \theta \textbf{i}_{z}\))
Usando el teorema de divergencia probar el teorema de Green
\(\oint_{S}[f \nabla g - g \nabla f] \cdot \textbf{dS} = \int_{V} [f \nabla^{2} g - g \nabla^{2} f] dV\)
(Pista:\(\nabla \cdot (f \nabla g) = f \nabla^{2} g + \nabla f \cdot \nabla g.\))
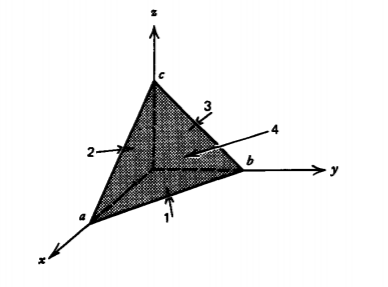
(a) Encontrar el elemento área\(\textbf{dS} \) (magnitud y dirección) en cada una de las cuatro superficies de la figura piramidal mostrada.
(b) Encontrar el flujo del vector
\(\textbf{A} = r \textbf{i}_{r} = x \textbf{i}_{x} + y \textbf{i}_{y} + z \textbf{i}_{z}\)
a través de la superficie de (a).
c) Verificar el teorema de divergencia evaluando también el flujo como
\(\Phi = \int_{V} \nabla \cdot \textbf{A} dV\)
Sección 1-5
Encuentra el curl de los siguientes vectores:
(a)\(\textbf{A} = x^{2} y \textbf{i}_{x} + y^{2} z \textbf{i}_{y} + x y \textbf{i}_{z}\)
b)\(\textbf{A} = \textrm{r} \: \cos \: \phi \textbf{i}_{z} + \frac{z \: \sin \: \phi}{\textrm{r}} \textbf{i}_{\textrm{r}}\)
c)\(\textbf{A} = r^{2} \sin \: \theta \: \cos \: \phi \: \textbf{i}_{r} + \frac{\cos \: \theta \: \sin \: \phi}{r^{2}} \textbf{i}_{\theta}\)
Usando el teorema de Stokes demostrar que
\(\oint_{L} f \: \textbf{dl} = - \int_{S} \nabla f \times \textbf{dS}\)
(Pista: Let\(\textbf{A}=\textbf{i}f\), donde\(\textbf{i}\) está cualquier vector de unidad constante.)
Verificar el teorema de Stokes para el contorno delimitador rectangular en el\(xy\) plano con un campo vectorial
\(\textbf{A} = (x + a)(y + b)(z + c) \textbf{i}_{x}\)
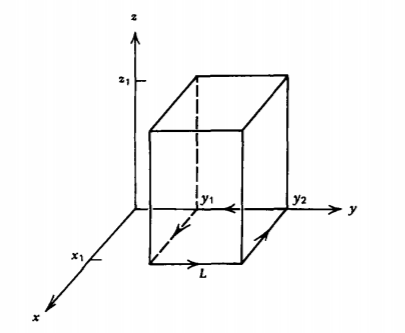
Verifique el resultado para (a) una superficie rectangular plana en el \(xy\)plano, y (b) para el cilindro rectangular.
Mostrar que el orden de diferenciación para la segunda derivada mixta
\(\frac{\partial}{\partial x} (\frac{\partial f}{\partial y}) = \frac{\partial}{\partial y}(\frac{\partial f}{\partial x})\)
no importa para la función
\(f = \frac{x^{2} \ln \: y}{y}\)
Algunos de los vectores unitarios en coordenadas cilíndricas y esféricas cambian de dirección en el espacio y así, a diferencia de los vectores unitarios cartesianos, no son vectores constantes. Esto significa que las derivadas espaciales de estos vectores unitarios son generalmente distintas de cero. Encuentra la divergencia y rizo de todos los vectores unitarios.
Un sistema general de coordenadas curvilíneas ortogonales diestras se describe mediante variables\(\left ( u,v,w \right )\), donde
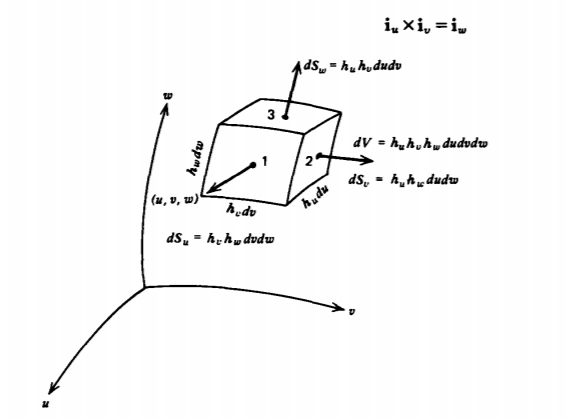
Dado que las cantidades de coordenadas incrementales\(du\)\(dv\), y\(dw\) no necesariamente tienen unidades de longitud, los elementos de longitud diferencial deben multiplicarse por coeficientes que generalmente son una función de\(u\),\(v\), y\(w\):
\(dL_{u} = h_{u}du, \: \: dL_{v} = h_{v}dv, \: \: dL_{w} = h_{w}dw\)
a) ¿Cuáles son los \(h\)coeficientes para los sistemas de coordenadas cartesianas, cilíndricas y esféricas?
b) ¿Cuál es el gradiente de cualquier función\(f\left ( u,v,w \right )\)?
c) ¿Cuál es el área de cada superficie y el volumen de un elemento de volumen de tamaño diferencial en el\(\left ( u,v,w \right )\) espacio?
d) ¿Cuáles son el rizo y la divergencia del vector?
\(\textbf{A} = A_{u}\textbf{i}_{u} + A_{v}\textbf{i}_{v} + A_{w} \textbf{i}_{w}\)?
e) ¿Qué es el escalar laplaciano\(\nabla^{2} f = \nabla \cdot (\nabla f)\)?
(f) Verifique sus resultados de (b) - (e) para los tres sistemas básicos de coordenadas.
Demostrar las siguientes identidades vectoriales:
(a)\(\nabla(fg) = f \nabla g + g \nabla f\)
b)\(\nabla(\textbf{A} \cdot \textbf{B}) = (\textbf{A} \cdot \nabla) \textbf{B} + (\textbf{B} \cdot \nabla) \textbf{A} + \textbf{A} \times (\nabla \times \textbf{B}) + \textbf{B} \times (\nabla \times \textbf{A})\)
c)\(\nabla \cdot (f \textbf{A}) = f \nabla \cdot \textbf{A} + (\textbf{A} \cdot \nabla ) \)
d)\(\nabla \cdot (\textbf{A} \cdot \textbf{B}) = \textbf{B} \cdot (\nabla \times \textbf{A}) - \textbf{A} \cdot (\nabla \times \textbf{B})\)
e)\(\nabla \times (\textbf{A} \times \textbf{B}) = \textbf{A}(\nabla \cdot \textbf{B}) - \textbf{B}(\nabla \cdot \textbf{A}) + (\textbf{B} \cdot \nabla) \textbf{A} - (\textbf{A} \cdot \nabla) \textbf{B}\)
f)\(\nabla \times (f \textbf{A}) = \nabla f \times \textbf{A} + f \nabla \times \textbf{A}\)
g)\(\nabla \times \textbf{A}) \times \textbf{A} = (\textbf{A} \cdot \nabla) \textbf{A} - \frac{1}{2} \nabla (\textbf{A} \cdot \textbf{A})\)
h)\(\nabla \times (\nabla \times \textbf{A}) = \nabla (\nabla \cdot \textbf{A}) - \nabla^{2} \textbf{A}\)
Dos puntos tienen coordenadas cartesianas\((1, 2, -1)\) y\((2, -3, 1)\).
a) ¿Cuál es la distancia entre estos dos puntos?
b) ¿Cuál es el vector unitario a lo largo de la línea que une los dos puntos?
(c) Encontrar un vector unitario en el\(xy\) plano perpendicular al vector unitario que se encuentra en (b).
Varios
Un circuito RLC serie ofrece una buena revisión en la resolución de ecuaciones diferenciales ordinarias de coeficiente constante lineal. \(V_0\)Se aplica un voltaje de paso al circuito inicialmente no excitado en\(t =0\).
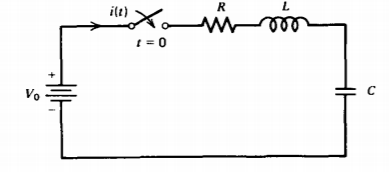
(a) Escribir una única ecuación diferencial para la corriente.
(b) Adivina una solución exponencial de la forma
\(i(t) = \hat{I}e^{st}\)
y encontrar las frecuencias naturales del circuito.
c) ¿Cuáles son las condiciones iniciales? ¿Cuáles son los voltajes de estado estacionario en cada elemento?
(d) Escribir y esbozar la solución para \(i\left ( t \right )\)cuando
\((\frac{R}{2L})^{2} < \frac{1}{LC'} \: (\frac{R}{2L})^{2} = \frac{1}{LC'} \: (\frac{R}{2L})^{2} \> \frac{1}{LC}\)
e) ¿Cuál es el voltaje en cada elemento?
(f) Una vez que el circuito ha alcanzado el estado estacionario, el voltaje del terminal se cortocircuita instantáneamente. ¿Cuál es la corriente de cortocircuito?
Muchas veces en este texto consideramos sistemas compuestos por secuencias repetitivas de un bloque de construcción básico. Dichos sistemas de elementos discretos se describen mediante ecuaciones de diferencia. Considere un sistema de capacitancia de inductancia-derivación en serie distribuida excitado por una frecuencia sinusoidal de\(\omega\) modo que el voltaje y la corriente en el bucle\(n\) th varíen como
\(i_{n} = \textrm{Re} (I_{n}e^{j \omega t}); \: \: v_{n} = \textrm{Re}(V_{n} e^{j \omega t})\)
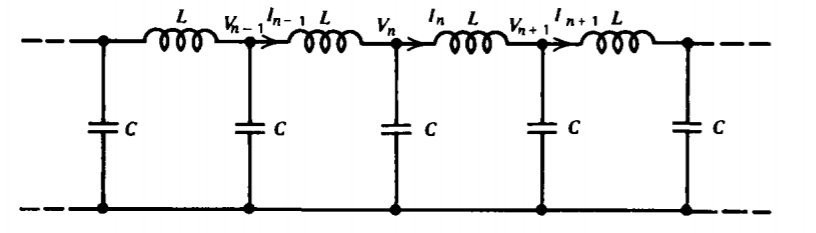
(a) Al escribir la ley de voltaje de Kirchoff para el\(\) n-ésimo bucle, mostrar que la corriente obedece a la ecuación de diferencia
\(I_{n + 1} - (2 = \frac{\omega^{2}}{\omega_{0}^{2}}) I_{n} + I_{n-1} = 0\)
¿Qué es\(\omega_{o}^{2}\)?
(b) Así como las soluciones exponenciales satisfacen ecuaciones diferenciales de coeficientes constantes lineales, las soluciones de ley de potencia satisfacen ecuaciones de diferencia de coeficientes constantes lineales
\(I_{n} = \hat{I} \lambda^{n}\)
¿Qué valores de\(\lambda\) satisfacer (a)?
c) La solución general a (a) es una combinación lineal de todas las soluciones posibles. La escalera de circuito que tiene\(N\) nodos es excitada en el bucle cero por una fuente de corriente
\(i_{0} = \textrm{Re}(I_{0}e^{j \omega t}\)
Encuentre la expresión general de corriente\(i_{n}\) y voltaje\(v_{n}\) para cualquier bucle cuando el último bucle\(N\) esté abierto (\(I_{N} = 0\)) o cortocircuitado (\(V_{N} = 0\)). (Pista:\(a + \sqrt{a^{2} - 1} = 1/(a = \sqrt{a^{2} -1})\)
d) ¿Cuáles son las frecuencias naturales del sistema cuando el último bucle está abierto o cortocircuitado?
(Pista:\((1)^{1/(2N)} = e^{j 2 \pi r/2N}, \: \: r = 1, 2, 3, ...., 2N.)\)


