5.1: Fuerzas en cargos por movimiento

5-1-1 La Ley de Fuerza Lorentz

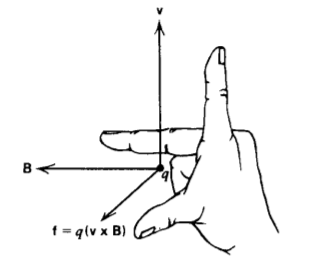
Era bien sabido que los imanes ejercen fuerzas unos sobre otros, pero en 1820 Oersted descubrió que un imán colocado cerca de un cable portador de corriente se alineará perpendicular al alambre. Cada carga q en el alambre, moviéndose con velocidad v en el campo magnético B [teslas, (kg-s ^-2 -A ^-1)], sintió la fuerza Lorentz determinada empíricamente perpendicular tanto a v como a B

\[\textbf{f} = q( \textbf{v} \times \textbf{B}) \nonumber \]

como se ilustra en la Figura 5-1. Una distribución de carga siente una fuerza diferencial df en cada elemento de carga incremental móvil dq:

\[d \textbf{f} = dq (\textbf{V} \times \textbf{B}) \nonumber \]

Figura 5-1 Una carga que se mueve a través de un campo magnético experimenta la fuerza de Lorentz perpendicular tanto a su movimiento como al campo magnético.

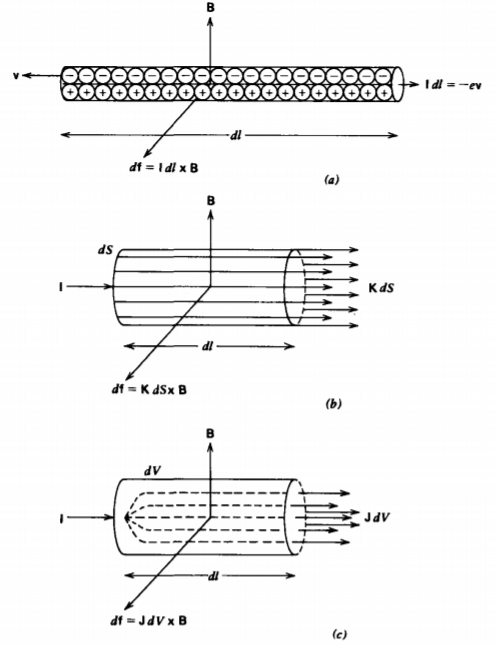
Las cargas móviles sobre una línea, superficie o volumen, constituyen respectivamente corrientes de línea, superficie y volumen, como en la Figura 5-2, donde (2) se convierte en

\[d \textbf{f} = \left \{ \begin{matrix} \rho_{f} \textbf{v} \times \textbf{B} dV = \textbf{J} \times \textbf{B} dV & (\textbf{J} = \rho_{f} \textbf{v}, \: \textrm{ volume current density} ) \\ \sigma_{f} \textbf{v} \times \textbf{B} dS = \textbf{K} \times \textbf{B} dS & (\textbf{K} = \sigma_{f} \textbf{v}, \: \textrm{ surface current density}) \\ \lambda_{f} \textbf{v} \times \textbf{B} dl = \textbf{I} \times \textbf{B} dl & (\textbf{I} = \lambda_{f} \textbf{v}, \: \textrm{line current} ) \end{matrix} \right. \nonumber \]

Figura 5-2 Las distribuciones de carga en línea móvil, superficie y volumen constituyen corrientes. (a) En alambres metálicos la carga neta es cero ya que hay cantidades iguales de cargas negativas y positivas para que la fuerza coulómbica sea cero. Dado que la carga positiva es esencialmente estacionaria, solo los electrones móviles contribuyen a la corriente de línea en la dirección opuesta a su movimiento. (b) Corriente superficial. (c) Corriente de volumen.

La fuerza magnética total sobre una distribución de corriente se obtiene entonces integrando (3) sobre el volumen total, superficie o contorno que contiene la corriente. Si hay una carga neta con su campo eléctrico asociado E, las densidades de fuerza totales incluyen la contribución coulómbica:

\[\textbf{f} = q (\textbf{E} + \textbf{v} \times \textbf{B}) \: \textrm{ Newton} \\ \textbf{F}_{L} = \lambda_{f} (\textbf{E} + \textbf{V} \times \textbf{B}) = \lambda_{f} \textbf{E} + \textbf{I} \times \textbf{B} \: \textrm{ N/m} \\ \textbf{F}_{S} = \sigma_{f} (\textbf{E} + \textbf{v} \times \textbf{B}) = \sigma_{f} \textbf{E} + \textbf{K} \times \textbf{B} \: \textrm{ N/m^{2}} \\ \textbf{F}_{V} = \rho_{f} (\textbf{E} + \textbf{v} \times \textbf{B}) = \rho_{f} \textbf{E} + \textbf{J} \times \textbf{B} \: \textrm{ N/m^{3}} \nonumber \]

En muchos casos la carga neta en un sistema es muy pequeña por lo que la fuerza coulómbica es despreciable. Esto suele ser cierto para la conducción en cables metálicos. Una corriente neta sigue fluyendo debido a la diferencia de velocidades de cada portador de carga.

A diferencia del campo eléctrico, el campo magnético no puede cambiar la energía cinética de una carga móvil ya que la fuerza es perpendicular a la velocidad. Puede alterar la trayectoria de la carga pero no su magnitud de velocidad.

5-1-2 Movimientos de Carga en un Campo Magnético Uniforme

Los tres componentes de la ley de Newton para una carga q de masa m que se mueve a través de un campo magnético uniforme\(B_{z} \textbf{i}_{z}\) son

\[m \frac{d \textbf{v}}{dt} = q \textbf{v} \times \textbf{B} \Rightarrow \left \{ \begin{matrix} m \frac{dv_{x}}{dt} = q v_{y} B_{z} \\ m \frac{dv_{y}}{dt} = - qv_{x}B_{z} \\ m \frac{dv_{z}}{dt} = 0 \Rightarrow v_{z} = \textrm{const} \end{matrix} \right. \nonumber \]

La componente de velocidad a lo largo del campo magnético no se ve afectada. Resolver la primera ecuación\(v_{y}\) y sustituir el resultado por la segunda ecuación nos da una sola ecuación en\(v_{x}\):

\[\frac{d^{2}v_{x}}{dt^{2}} + \omega_{0}^{2}v_{x} = 0, \: \: \: \: v_{y} = \frac{1}{\omega_{0}} \frac{dv_{x}}{dt}, \: \: \: \: \omega_{0} = \frac{qB_{z}}{m} \nonumber \]

donde\(\omega_{0}\) se llama la velocidad angular de Larmor o la frecuencia del ciclotrón (ver Sección 5-1-4). Las soluciones a (6) son

\[v_{x} = A_{1} \sin \omega_{0} t + A_{2} \cos \omega_{0} t \\ v_{y} = \frac{1}{\omega_{0}} \frac{dv_{x}}{dt} = A_{1} \cos \oemga_{0} t - A_{2} \sin \omega_{0} t \nonumber \]

donde\(A_{1}\) y\(A_{2}\) se encuentran a partir de las condiciones iniciales. Si en t =0,

\[\textbf{v}(t = 0) = v_{0} \textbf{i}_{x} \nonumber \]

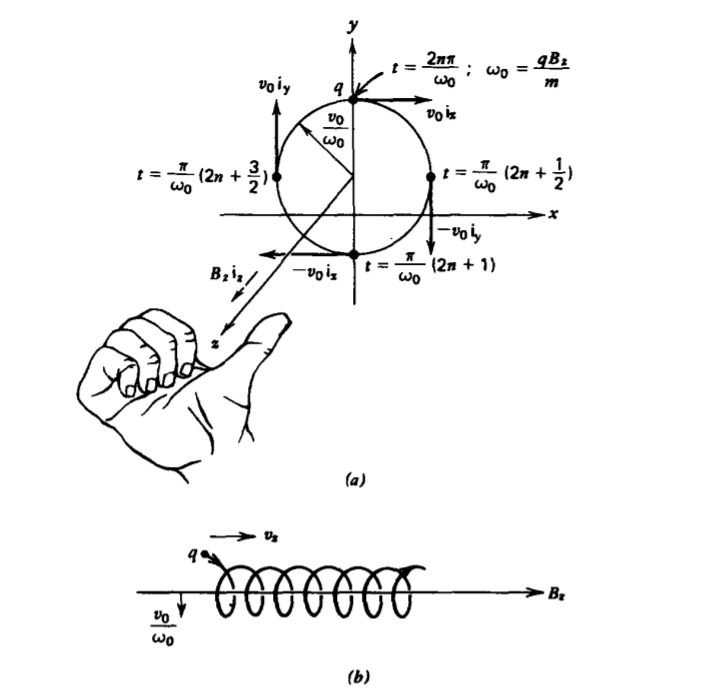
luego (7) y la Figura 5-3a muestran que la partícula viaja en círculo, con velocidad constante\(v_{0}\) en el plano xy:

\[v = v_{0} (\cos \omega_{0} t \textbf{i}_{x} - \sin \omega_{0} t \textbf{i}_{y}) \nonumber \]

con radio

\[R = v_{0}/\omega_{0} \nonumber \]

Si la partícula también tiene un componente de velocidad a lo largo del campo magnético en la dirección z, la trayectoria de carga se convierte en una hélice, como se muestra en la Figura 5-3b.

Figura 5-3 (a) Una carga positiva q, inicialmente moviéndose perpendicular a un campo magnético, siente una fuerza ortogonal poniendo la carga en un movimiento circular alrededor del campo magnético donde la fuerza de Lorentz se equilibra por la fuerza centrífuga. Tenga en cuenta que la carga viaja en la dirección (en este caso en el sentido de las agujas del reloj) de manera que su campo propio a través del bucle [ver Sección 5-2-1] es opuesto en dirección al campo aplicado. (b) Una componente de velocidad en la dirección del campo magnético no se ve afectada dando como resultado una trayectoria helicoidal.

5-1-3 El Espectrógrafo de Masas

El espectrógrafo de masas utiliza el movimiento circular derivado en la Sección 5-1-2 para determinar las masas de iones y medir las proporciones relativas de isótopos, como se muestra en la Figura 5-4. Las cargas entran entre electrodos de placa paralelos con una distribución de velocidad dirigida y. Para seleccionar aquellas cargas con una magnitud particular de velocidad, se imponen campos eléctricos y magnéticos perpendiculares para que la fuerza neta sobre una carga sea

\[f_{x} = q(E_{x} + v_{y}B_{z}) \nonumber \]

Para que las cargas pasen por la hendidura estrecha al final del canal, no deben ser desviadas por los campos para que la fuerza en (11) sea cero. Para una velocidad seleccionada\(v_{y} = v_{0}\) esto requiere un campo eléctrico dirigido negativamente x

que se ajusta fijando el voltaje aplicado V. Una vez que la carga pasa por la hendidura, ya no siente el campo eléctrico y sólo está bajo la influencia del campo magnético. Se desplaza así en un círculo de radio

\[r = \frac{v_{0}}{\omega_{0}} = \frac{v_{0}m}{q B_{0}} \nonumber \]

Figura 5-4 El espectrógrafo de masas mide la masa de un ion por el radio de su trayectoria cuando se mueve perpendicular a un campo magnético. El campo eléctrico uniforme cruzado selecciona la velocidad iónica que puede pasar a través de la hendidura.

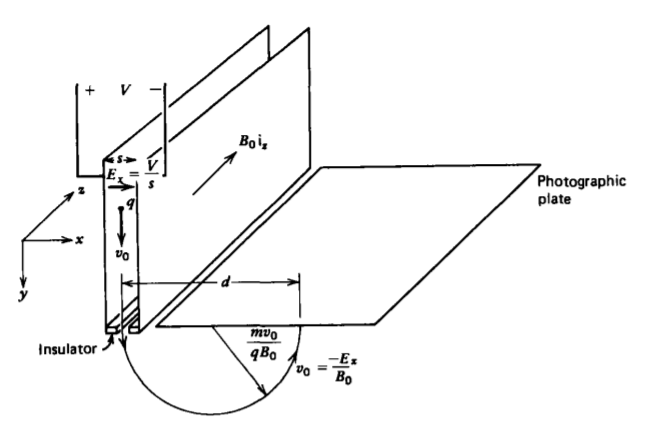
que es directamente proporcional a la masa del ion. Al medir la posición de la carga cuando golpea la placa fotográfica, se puede calcular la masa del ion. Diferentes isótopos que tienen el mismo número de protones pero diferentes cantidades de neutrones golpearán la placa en diferentes posiciones.

Por ejemplo, si el espectrógrafo de masas tiene un voltaje aplicado de V = -100 V a través de un espacio de 1 cm (E _x = -10 ⁴ V/m) con un campo magnético de 1 tesla, solo iones con velocidad

\[v_{y} = - E_{x}/B_{0} = 10^{4} \textrm{m/sec} \nonumber \]

pasará a través. Los tres isótopos de magnesio, ₁₂ Mg ²⁴, ₁₂ Mg ²⁵, ₁₂ Mg ²⁶, cada uno deficiente de un electrón, golpearán la placa fotográfica en las posiciones respectivas:

\[d = 2r = \frac{2 \times 10^{4} N (1.67 \times 10^{-27})}{1.6 \times 10^{-19} (1)} \approx 2 \times 10^{-4} N \Rightarrow 0.48, 0.50, 0.52 \textrm{cm} \nonumber \]

donde N es el número de protones y neutrones (m = 1.67 x ^10-27 kg) en el núcleo.

5-1-4 El Ciclotrón

Un ciclotrón lleva las partículas cargadas a velocidades muy altas por muchas pequeñas aceleraciones repetidas. Básicamente se compone de un cilindro hueco partido, como se muestra en la Figura 5-5, donde cada mitad se llama “dee” porque su forma es similar a la

Figura 5-5 El ciclotrón lleva iones a alta velocidad por muchas pequeñas aceleraciones repetidas por el campo eléctrico en la brecha entre des. Dentro de los dees el campo eléctrico es insignificante por lo que los iones se mueven en órbitas circulares cada vez más grandes debido a un campo magnético aplicado perpendicular a su movimiento.

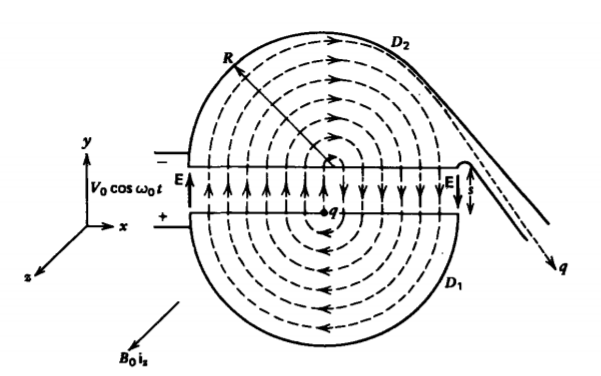
cuarta letra del alfabeto. Los dees se ponen en una diferencia de potencial sinusoidalmente variable. \(B_{0} \textbf{i}_{z}\)Se aplica un campo magnético uniforme a lo largo del eje del cilindro. El campo eléctrico es esencialmente cero dentro del volumen cilíndrico y se supone uniforme\(E_{y} =v(t)/s\) en el pequeño espacio entre los ejes. Una fuente de carga en el centro de\(D_{1}\) emite una carga q de masa m con velocidad cero en el pico de la tensión aplicada a t = 0. El campo eléctrico en el hueco acelera la carga hacia D ₂. Debido a que el hueco es tan pequeño, el voltaje permanece aproximadamente constante en V ₀ mientras la carga viaja entre dees de manera que su desplazamiento y velocidad son

\[m \frac{dv_{y}}{dt} = \frac{qV_{0}}{\textrm{s}} \Rightarrow v_{y} = \frac{qV_{0}}{sm} t \\ v_{y} = \frac{dy}{dt} \Rightarrow y = \frac{qV_{0}t^{2}}{2 ms} \nonumber \]

De esta manera, la carga entra en D ₂ en el momento\(t = [ 2ms^{2}/q \textrm{V}_{0}]^{1/2}\) posterior con velocidad\(v_{y} = \sqrt{2qV_{0}/m}\). Dentro\(D_{2}\) del campo eléctrico es insignificante por lo que la carga viaja en una órbita circular de radio\(r = v_{y}/\omega_{0} = m v_{y} /q B_{0}\) debido solo al campo magnético. La frecuencia del voltaje se ajusta para igualar apenas la velocidad angular\(\omega_{0} = q B_{0}/m\) de la carga, de manera que cuando la carga vuelve a entrar en el hueco entre dees la polaridad se ha invertido acelerando- la carga hacia D ₁ con mayor velocidad. Este proceso se repite continuamente, ya que cada vez que la carga entra en el hueco la polaridad del voltaje acelera la carga hacia la dee opuesta, resultando en un radio de recorrido mayor. Cada vez que la carga cruza el hueco su velocidad se incrementa en la misma cantidad de modo que después de que n brecha atraviese su velocidad y radio de órbita son

\[v_{n} = \bigg( \frac{2qnV_{0}}{m} \bigg) ^{1/2}, \: \: \: \: R_{n} = \frac{v_{n}}{\omega_{0}} = \bigg( \frac{2 nm V_{0}}{qB_{0}^{2}} \bigg) ^{1/2} \nonumber \]

Si el radio exterior de los ejes es R, la velocidad máxima de la carga

\[v_{\textrm{max}} = \omega_{0}R = \frac{qB_{0}}{m} R} \nonumber \]

se llega después de viajes de\(2n = qB_{0}^{2}R^{2}/mV_{0}\) ida y vuelta cuando\(R_{n} = R\). Para un ion hidrógeno (\(q = 1.6 \times 10^{-19}\)coul,\(m = 1.67 \times 10^{-27}\) kg), dentro de un campo magnético de 1 tesla (\(\omega_{0} \approx 9.6 \times 10^{7}\)radián/seg) y voltaje pico de 100 voltios con un radio de ciclotrón de un metro, alcanzamos\(v_{\textrm{max}} = 9.6 \times 10^{7}\) m/s (que es aproximadamente 30% de la velocidad de la luz) en aproximadamente\(2n \approx 9.6 \times 10^{5}\) viajes de ida y vuelta, lo que lleva un tiempo \( \tau = 4 n \pi/\omega_{0} \approx 2 \pi/100 \approx 0.06\)sec. Para llegar a esto

velocidad con un acelerador electrostático requeriría

\[\frac{1}{2} mv^{2} = qV \Rightarrow V = \frac{mv^{2}_{\textrm{max}}}{2q} \approx 48 \times 10^{6} \textrm{Volts} \nonumber \]

El ciclotrón trabaja a voltajes mucho menores debido a que la velocidad angular de los iones permanece constante para fijo\(qB_{0}/m\) y así llega al hueco en fase con el pico de la tensión aplicada para que se acelere secuencialmente hacia la dee opuesta. No se usa con electrones porque su pequeña masa les permite alcanzar velocidades relativistas cercanas a la velocidad de la luz, lo que luego aumenta enormemente su masa, disminuyendo su velocidad angular\(\omega\), poniéndolos fuera de fase con la tensión.

5-1-5 Efecto Hall

Cuando las cargas fluyen perpendicularmente a un campo magnético, el desplazamiento transversal debido a la fuerza de Lorentz puede dar lugar a un campo eléctrico. La geometría de la Figura 5-6 tiene un campo magnético uniforme\(B_{0} \textbf{i}_{z}\) aplicado a un material que transporta una corriente en la dirección y. Para cargas positivas como para agujeros en un semiconductor tipo p, la velocidad de carga también está en la dirección y positiva, mientras que para cargas negativas como ocurren en metales o en semiconductores de tipo n, la velocidad de carga está en la dirección y negativa. En el estado estacionario donde la velocidad de carga no varía con el tiempo, la fuerza neta sobre las cargas debe ser cero,

Figura 5-6 Un campo magnético perpendicular a un flujo de corriente desvía las cargas transversalmente dando lugar a un campo eléctrico y a la tensión Hall. La polaridad de la tensión es la misma que la señal de los portadores de carga.

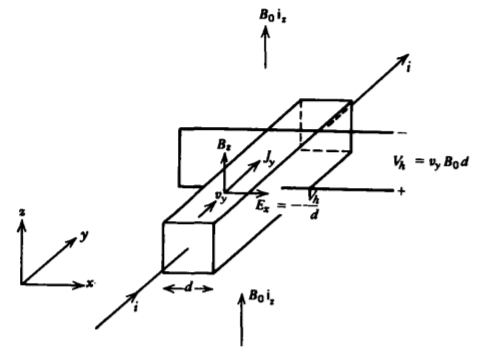
que requiere la presencia de un campo eléctrico dirigido x

\[\textbf{E} + \textbf{v} \times \textbf{B} = 0 \Rightarrow E_{x} = - v_{y} B_{0} \nonumber \]

Luego se desarrolla una diferencia de potencial transversal a través del material llamado voltaje Hall:

\[V_{h} = - \int_{0}^{d} E_{x} dx = v_{y} B_{0} d \nonumber \]

El voltaje Hall tiene su polaridad dada por el signo de\(v_{y}\); voltaje positivo para portadores de carga positiva y voltaje negativo para cargas negativas. Esta medición proporciona una manera fácil de determinar el signo del portador de carga predominante para la conducción.