5.5: Magnetización

Nuestro desarrollo hasta ahora se ha restringido a campos magnéticos en el espacio libre derivados de distribuciones de corriente impuestas. Así como pequeños desplazamientos de carga en materiales dieléctricos contribuyeron al campo eléctrico, los movimientos atómicos constituyen corrientes microscópicas, que también contribuyen al campo magnético. Existe una analogía directa entre polarización y magnetización, por lo que nuestro desarrollo será paralelo al de la Sección 3-1.

5-5-1 El dipolo magnético

Los modelos atómicos clásicos describen un átomo como electrones orbitantes alrededor de un núcleo cargado positivamente, como en la Figura 5-13.

Figura 5-13 Las corrientes atómicas surgen de electrones orbitando además de las contribuciones de espín del electrón y el núcleo

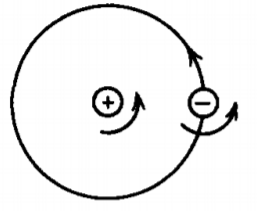
También se puede imaginar que el núcleo y el electrón están girando. El modelo más simple para estas corrientes atómicas es análogo al dipolo eléctrico y consiste en un pequeño bucle de corriente de área d S que transporta una corriente I, como en la Figura 5-14. Debido a que las dimensiones atómicas son tan pequeñas, sólo nos interesa el campo magnético lejos de este dipolo magnético. Entonces la forma del bucle no es importante, así por simplicidad lo tomamos como rectangular

El potencial de vector para este bucle es entonces

\[\textbf{A} = \frac{\mu_{0}I}{4 \pi} \bigg[ dx \bigg(\frac{1}{r_{3}} - \frac{1}{r_{1}} \bigg) \textbf{i}_{x} + dy \bigg( \frac{1}{r_{4}} - \frac{1}{r_{2}} \bigg) \textbf{i}_{y} \bigg] \nonumber \]

donde asumimos que la distancia desde cualquier punto de cada lado del bucle hasta el punto de campo P es aproximadamente constante.

Figura 5-14 Un dipolo magnético consiste en un pequeño bucle de corriente circulante. El momento magnético está en la dirección normal al bucle por la regla de la derecha.

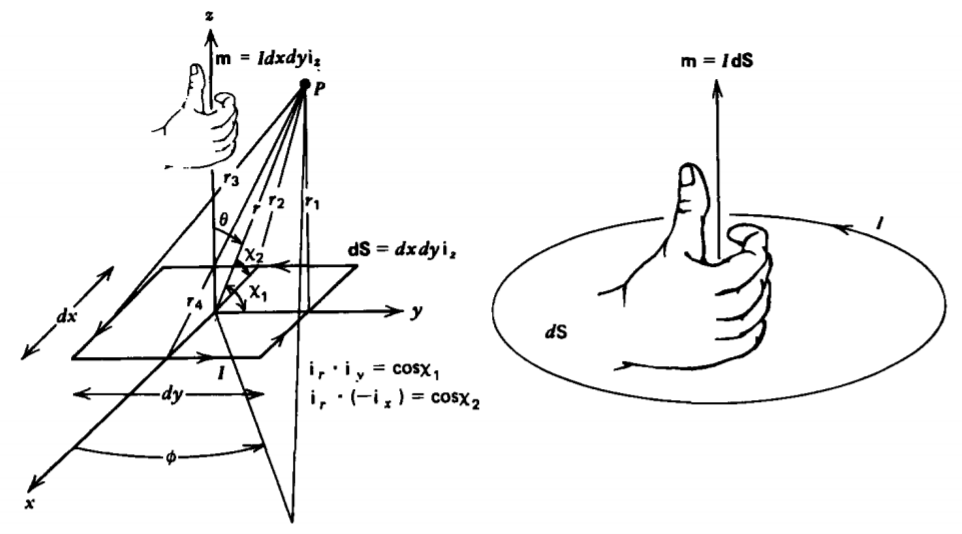
Utilizando la ley de los cosenos, estas distancias se relacionan como

\[r_{1}^{2} = r^{2} + \bigg( \frac{dy}{2} \bigg) ^{2} - r dy \cos \chi_{1}; \: \: \: \: r_{2}^{2} = r^{2} + \bigg( \frac{dx}{2} \bigg)^{2} - r dx \cos \chi_{2} \\ r_{3}^{2} = r^{2} + \bigg( \frac{dy}{2} \bigg)^{2} + r dy \cos \chi_{1}, \: \: \: \: r_{4}^{2} = r^{2} + \bigg( \frac{dx}{2} \bigg) ^{2} + r dx \cos \chi_{2} \nonumber \]

donde los ángulos\(\chi_{1}\) y\(\chi_{2}\) están relacionados con las coordenadas esféricas de la Tabla 1-2 como

\[\textbf{i}_{r} \cdot \textbf{i}_{y} = \cos \chi_{1} = \sin \theta \sin \phi \\ - \textbf{i}_{r} \cdot \textbf{i}_{x} = \cos \chi_{2} = - \sin \theta \cos \phi \nonumber \]

En el campo lejano, el límite (1) se convierte

\[\lim_{r >> dx \\ d >> dy} \textbf{A} = \frac{\mu_{0}I}{4 \pi} \bigg[ \frac{dx}{r} \bigg( \frac{1}{\bigg[ 1 + \frac{dy}{dr} \bigg( \frac{dy}{2r} + 2 \cos \chi_{1} \bigg) \bigg] ^{1/2}} \\ - \frac{1}{\bigg[1 + \frac{dy}{2r} \bigg( \frac{dy}{2r} - 2 \cos \chi_{1} \bigg) \bigg]^{1/2} } \bigg) \\ + \frac{dy}{r} \bigg( \frac{1}{\bigg[ 1 + \frac{dx}{2r} \bigg( \frac{dx}{2r} + 2 \cos \chi_{2} \bigg) \bigg]^{1/2}} - \frac{1}{\bigg[ 1 + \frac{dx}{2r} \bigg( \frac{dx}{2r} -2 \cos \chi_{2} \bigg) \bigg]^{1/2}} \bigg) \bigg] \approx \frac{- \mu_{0}I}{4 \pi r^{2}} dx dy [ \cos \chi_{1} \textbf{i}_{x} + \cos\chi_{2} \textbf{i}_{y}] \nonumber \]

El uso de (3), (4) reduce aún más a

\[\textbf{A} = \frac{\mu_{0}I d \textrm{S}}{4 \pi r^{2}} \sin \theta [ - sin \phi \textbf{i}_{x} + \cos \phi \textbf{i}_{y} ] \\ = \frac{\mu_{0}I d \textrm{S}}{4 \pi r^{2}} \sin \theta \textbf{i}_{\phi} \nonumber \]

donde nuevamente usamos la Tabla 1-2 para escribir el término de vector de unidad cartesiana entre corchetes como\(\textbf{i}_{\phi}\). El momento dipolo magnético m se define como el vector en la dirección perpendicular al bucle (en este caso\(\textbf{i}_{z}\)) por la regla de la derecha con magnitud igual al producto de la corriente y el área del bucle:

\[\textbf{m} = I \: d \textrm{S} \textbf{i}_{z} = I \: \textbf{dS} \nonumber \]

Entonces el potencial vectorial puede escribirse de manera más general como

\[\textbf{A} = \frac{\mu_{0}m}{4 \pi r^{2}} \sin \theta \textbf{i}_{\phi} = \frac{\mu_{0} \textbf{m}}{4 \pi r^{2}} \times \textbf{i}_{r} \nonumber \]

con campo magnético asociado

\[\textbf{B} = \nabla \times \textbf{A} = \frac{1}{r \sin \theta} \frac{\partial}{\partial \theta} (A_{\phi} \sin \theta) \textbf{i}_{r} - \frac{1}{r} \frac{\partial}{\partial r} (r A_{\phi}) \textbf{i}_{\phi} \\ = \frac{\mu_{0} m}{4 \pi r^{3}} [2 \cos \theta \textbf{i}_{r} + \sin \theta \textbf{i}_{\theta}] \nonumber \]

Este campo es idéntico en forma al campo dipolar eléctrico de la Sección 3-1-1 si reemplazamos\(p/\varepsilon_{0}\) por\(\mu_{0} m\).

5-5-2 Corrientes de Magnetización

Amperios modelaron materiales magnéticos como teniendo el volumen llenado con tales bucles de corriente circulante infinitesimal con densidad numérica N, como se ilustra en la Figura 5-15. El vector de magnetización M se define entonces como la densidad del dipolo magnético:

\[\textbf{M} = N \textbf{m} = NI \textbf{dS} \textrm{amp/m} \nonumber \]

Para el contorno de tamaño diferencial en el plano xy mostrado en la Figura 5-15, solo aquellos dipolos con momentos en las direcciones x o y (así z componentes de las corrientes) darán lugar a corrientes que cruzan perpendicularmente a través de la superficie delimitada por el contorno. Esos dipolos completamente dentro del contorno no dan corriente neta ya que la corriente pasa por el contorno dos veces, una vez en la dirección z positiva y en su retorno en la dirección z negativa. Sólo esos dipolos a cada lado de los bordes-para que la corriente sólo pase por el contorno una vez, con el retorno fuera del contorno-dan una corriente neta a través del bucle.

Debido a que la longitud de los lados del contorno\(\Delta x\) y\(\Delta y\) son de tamaño diferencial, asumimos que los dipolos a lo largo de cada borde no cambian de magnitud ni dirección. Entonces la corriente total neta vinculada por el contorno cerca de cada lado es igual al producto de la corriente por dipolo I y el número de dipolos que apenas pasan por el contorno una vez. Si el vector normal al bucle dipolo (en la dirección de m) forma un ángulo\(\theta\) con respecto a la dirección del lado del contorno en la posición x, la corriente neta vinculada a lo largo de la línea en x es

\[- IN d \textrm{S} \Delta y \cos \theta \big|_{x} = -M_{y}(x) \Delta y \nonumber \]

El signo menos surge porque la corriente dentro del contorno adyacente a la línea en la coordenada x fluye en la dirección - z.

Figura 5-15 Muchos de estos dipolos magnéticos dentro de un material que une un contorno cerrado dan lugar a una corriente de magnetización efectiva que también es fuente del campo magnético.

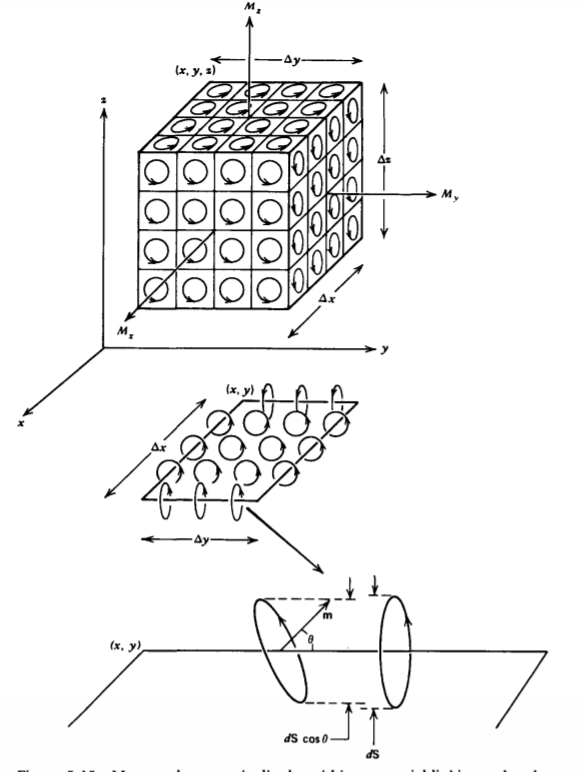
Del mismo modo, cerca del borde en la coordenada\(x + \Delta x \), la corriente neta vinculada perpendicular al contorno es

\[IN \: d \textrm{S} \Delta y \cos \theta \big|_{x + \Delta x} = M_{y} (x + \Delta x) \Delta y \nonumber \]

A lo largo de los bordes en y y\(y + \Delta y\), las contribuciones actuales son

\[IN \: d \textrm{S} \Delta x \: \cos \theta \big|_{y} = M_{x}(y) \Delta x \\ = - IN \: d \textrm{S} \: \Delta x \cos \theta \big|_{y + \Delta y} = - M_{x}(y + \Delta y) \Delta x \nonumber \]

La corriente total en la dirección z vinculada por este contorno es así la suma de contribuciones en (10) - (12):

\[I_{z \textrm{tot}} = \Delta x \Delta \bigg( \frac{M_{y} (x + \Delta x) - M_{y}(x)}{\Delta x} - \frac{M_{x}(y + \Delta y) - M_{x}(y)}{\Delta y}\bigg) \nonumber \]

Si la magnetización es uniforme, la corriente total neta es cero ya que la corriente que pasa por el bucle en un lado es cancelada por la corriente que fluye en dirección opuesta en el otro lado. Solo si la magnetización cambia con la posición puede haber una corriente neta a través de la superficie del bucle. Esto se puede lograr si bien la corriente por dipolo, área por dipolo, densidad de dipolos, de ángulo de orientación de los dipolos es una función de posición.

En el límite como\(\Delta x\) y\(\Delta y\) se vuelven pequeños, términos en el lado derecho en (13) definen derivadas parciales para que la corriente por unidad de área en la dirección z sea

\[\lim_{\Delta x \rightarrow 0 \\ \Delta y \rightarrow 0} J_{z} = \frac{I_{z \textrm{ tot}}}{\Delta x \Delta y} = \bigg( \frac{\partial M_{y}}{\partial x} - \frac{\partial M_{x}}{\partial y} \bigg) = ( \nabla \times \textbf{M})_{z} \nonumber \]

que reconocemos como el componente z del rizo de la magnetización. Si hubiéramos orientado nuestro bucle en los planos xz o yz, los componentes de densidad de corriente obedecerían de manera similar las relaciones

\[J_{y} = \bigg( \frac{\partial M_{x}}{\partial z} - \frac{\partial M_{z}}{\partial x} \bigg) = (\nabla \times \textbf{M})_{y} \\ J_{x} = \bigg( \frac{\partial M_{z}}{\partial y} - \frac{\partial M_{y}}{\partial z} \bigg) = (\nabla \times \textbf{M})_{x} \nonumber \]

donde subindicamos la densidad de corriente con una m para representar la densidad de corriente de magnetización, a menudo llamada densidad de corriente Amperiano.

Estas corrientes son también fuentes del campo magnético y pueden ser utilizadas en la ley de Ampere como

\[\nabla \times \frac{\textbf{B}}{\mu_{0}} = \textbf{J}_{m} + \textbf{J}_{f} = \textbf{J}_{f} + \nabla \times \textbf{M} \nonumber \]

donde\(\textbf{J}_{f}\) se encuentra la corriente libre debido al movimiento de cargas libres en contraste con la corriente de magnetización\(\textbf{J}_{m}\), que se debe al movimiento de cargas encuadernadas en los materiales.

Como solo podemos imponer corrientes libres, es conveniente definir el vector H como la intensidad del campo magnético a distinguir de B, que ahora llamaremos densidad de flujo magnético:

\[\textbf{H} = \frac{\textbf{B}}{\mu_{0}} - \textbf{M} \Rightarrow \textbf{B} = \mu_{0} (\textbf{H} + \textbf{M}) \nonumber \]

Entonces (17) se puede refundir como

\[\nabla \times \bigg( \frac{\textbf{B}}{\mu_{0}} - \textbf{M} \bigg) = \nabla \times \textbf{H} = \textbf{J}_{f} \nonumber \]

Las relaciones de divergencia y flujo de la Sección 5-3-1 no han cambiado y están en términos de la densidad de flujo magnético B. En el espacio libre, donde M = 0, la relación de (19) entre B y H se reduce a

\[\textbf{B} = \mu_{0} \textbf{H} \nonumber \]

Esto es análogo al desarrollo de la polarización con las relaciones de D, E y P. Obsérvese que en (18), el parámetro constante\(\mu_{0}\) multiplica tanto H como M, a diferencia de la permitividad\(\mu_{0}\) que solo multiplica E.

La ecuación (19) se puede poner en una forma integral equivalente usando el teorema de Stokes:

\[\int_{S} (\nabla \times \textbf{H}) \cdot \textbf{dS} = \oint_{L} \textbf{H} \cdot \textbf{dl} = \int_{S} \textbf{J}_{f} \cdot \textbf{dS} \nonumber \]

La densidad de corriente libre\(\textbf{J}_{f}\) es la fuente del campo H, la densidad de corriente de magnetización\(\textbf{J}_{m}\). es la fuente del campo M, mientras que la corriente total\(\textbf{J}_{f} + \textbf{J}_{m}\),, es la fuente del campo B.

5-5-3 Materiales Magnéticos

Existen analogías directas entre los procesos de polarización que se encuentran en los efectos dieléctricos y magnéticos. La ley constitutiva que relaciona la magnetización M con un campo magnético aplicado H se encuentra aplicando la fuerza Lorentz a nuestros modelos atómicos.

a) Diamagnetismo

Los electrones orbitantes como bucles de corriente atómica son análogos a la polarización electrónica, con la corriente en la dirección opuesta a su velocidad. Si el electrón (e = 1.6 x ^10-9 coul) gira a velocidad angular\(\omega\) en el radio R, como en la Figura 5-16, la corriente y el momento dipolar son

\[I = \frac{e \omega}{2 \pi}, \: \: \: \: m = I \pi R^{2} = \frac{e \omega}{2} R^{2} \nonumber \]

Figura 5-16 El electrón orbitante tiene su momento magnético m en la dirección opuesta a su momento angular L porque la corriente es opuesta a la velocidad del electrón.

Tenga en cuenta que el momento angular L y el momento magnético m están dirigidos de manera opuesta y están relacionados como

\[\textbf{L} = m_{e} R \textbf{i}_{r} \times \textbf{v} = m_{e} \omega R^{2} \textbf{i}_{z} = - \frac{2m_{e}}{e} \textbf{m} \nonumber \]

donde m _e = 9.1 x 10 ^-31 kg es la masa electrónica.

Dado que la teoría cuántica requiere que el momento angular se cuantifique en unidades de\(h/2 \pi\), donde la constante de Planck es\(h = 6.62 \times 10{-34}\) joule-seg, la unidad más pequeña de momento magnético, conocida como el magnetón Bohr, es

\[m_{B} = \frac{eh}{4 \pi m_{e}} \approx 9.3 \times 10^{-24} \textrm{amp m}^{2} \nonumber \]

Dentro de un material homogéneo estos dipolos se distribuyen aleatoriamente de manera que por cada electrón que orbita en una dirección, otro electrón cercano está orbitando en dirección opuesta para que en ausencia de un campo magnético aplicado no haya magnetización neta.

La fuerza de atracción coulómbica sobre el electrón orbitante hacia el núcleo con número atómico Z se equilibra por la fuerza centrífuga:

\[m_{e} \omega^{2} R = \frac{Z e^{2}}{4 \pi \varepsilon_{0}R^{2}} \nonumber \]

Dado que el lado izquierdo es solo proporcional al cuadrado del momento angular cuantificado, también se cuantifica el radio de órbita R para el que el valor más pequeño es

\[R = \frac{4 \pi \varepsilon_{0}}{m_{e}Ze^{2}} \bigg( \frac{h}{2 \pi} \bigg)^{2} \approx \frac{5 \times 10^{-11}}{Z} \textrm{m} \nonumber \]

con velocidad angular resultante

\[\omega = \frac{Z^{2}e^{4}m_{e}}{(4 \pi \varepsilon_{0})^{2}(h/2 \pi)^{3}} \approx 1.3 \times 10^{16}Z^{2} \nonumber \]

Cuando\(H_{0}\textbf{i}_{z}\) se aplica un campo magnético, como en la Figura 5-17, los bucles de electrones con momento magnético opuesto al campo sienten una fuerza radial adicional hacia adentro, mientras que los bucles con momento colineal y campo sienten una fuerza radial hacia afuera. Dado que el radio orbital R no puede cambiar porque está cuantificado, esta fuerza magnética da como resultado un cambio de velocidad orbital\(\Delta \omega\):

\[m_{e}(\omega + \Delta \omega_{1})^{2} R = e \bigg( \frac{Ze}{4 \pi \varepsilon_{0}R^{2}} + (\omega + \Delta \omega_{1}) R \mu_{0}H_{0} \bigg) \\ m_{e}(\omega + \Delta \omega_{2})^{2} R= e \bigg( \frac{Ze}{4 \pi \varepsilon_{0}R^{2}} - (\omega + \Delta \omega_{2}) R \mu_{0} H_{0} \bigg) \nonumber \]

donde el primer electrón acelera mientras que el segundo se ralentiza.

Debido a que el cambio de velocidad\(\Delta \omega\) es mucho menor que la velocidad natural\(\omega\), resolvemos (28) aproximadamente como

\[\Delta \omega_{1} = \frac{e \omega \mu_{0} H_{0}}{2 m_{e} \omega - e \mu_{0} H_{0}} \\ \Delta \omega_{2} = \frac{- e \omega \mu_{0} H_{0}}{2 m_{e} \omega + e \mu_{0} H_{0}} \nonumber \]

donde descuidamos cantidades de orden\((\Delta \omega)^{2}\). Sin embargo, incluso con intensidades de campo magnético muy altas de\(H_{0} 10^{6}\) amp/m vemos que generalmente

\[e \mu_{0} H_{0} << 2 m_{e} \omega_{0} \\ (1.6 \times 10^{-19})(4 \pi 10^{-7}) 10^{6} << 2(9.1 \times 10^{-31})(1.3 \times 10^{16}) \nonumber \]

de manera que (29) reduce aún más a

\[\Delta \omega_{1} \approx - \Delta \omega_{2} \approx \frac{e \mu_{0}H_{0}}{2 m_{e}} \approx 1.1 \times 10^{5} H_{0} \nonumber \]

El momento magnético neto para este par de bucles,

\[m = \frac{eR^{2}}{2} (\omega_{2} - \omega_{1}) = -eR^{2} \Delta \omega_{1} = \frac{- e^{2} \mu_{0}R^{2}}{2 m_{e}} H_{0} \nonumber \]

es opuesto en dirección al campo magnético aplicado.

Figura 5-17 Los efectos diamagnéticos, aunque generalmente pequeños, surgen en todos los materiales debido a que los dipolos con momentos paralelos al campo magnético tienen un incremento en la velocidad de los electrones orbitantes mientras que aquellos dipolos con momentos opuestos al campo tienen una disminución de velocidad. El radio del bucle permanece constante porque se cuantifica.

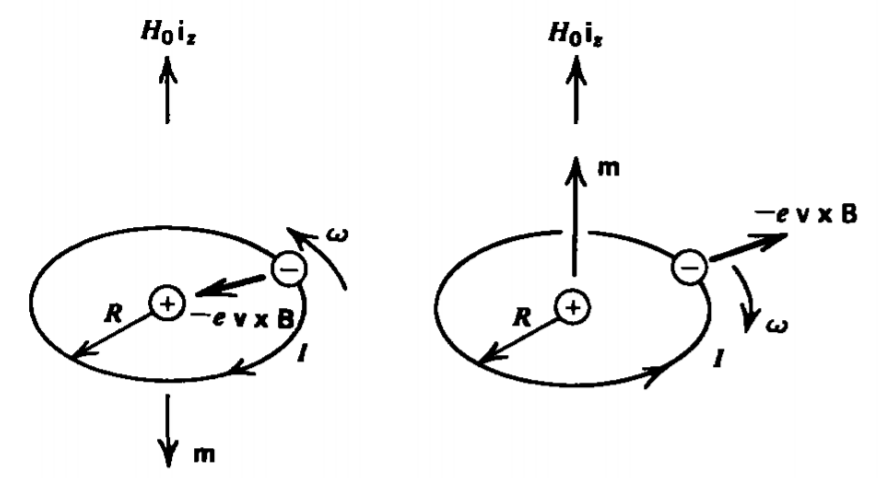
Si tenemos N pares de bucles por unidad de volumen, el campo de magnetización es

\[\textbf{M} = N \textbf{m} = - \frac{Ne^{2} \mu_{0} R^{2}}{2m_{e}} H_{0}\textbf{i}_{z} \nonumber \]

que también se dirige de manera opuesta al campo magnético aplicado

Dado que la magnetización está linealmente relacionada con el campo, definimos la susceptibilidad magnética\(\chi_{m}\) como

\[\textbf{M} = \chi_{m} \textbf{H}, \: \: \: \: \chi_{m} = - \frac{Ne^{2}\mu_{0}R^{2}}{2 m_{e}} \nonumber \]

donde\(\chi_{m}\) es negativo. La densidad de flujo magnético es entonces

\[\textbf{B} = \mu_{0}(\textbf{H} + \textbf{M}) = \mu_{0}(1 + \chi_{m}) \textbf{H} = \mu_{0} \mu_{r} \textbf{H} = \mu \textbf{H} \nonumber \]

donde\(\mu_{r} = 1 + \chi_{m}\) se llama la permeabilidad relativa y\(\mu\) es la permeabilidad. En el espacio libre\(\chi_{m} = 0 \) para que\(\mu_{r} = 1\) y\(\mu = \mu_{0}\). La última relación en (35) suele ser conveniente de usar, ya que todos los resultados en el espacio libre siguen siendo correctos dentro del material permeable lineal si reemplazamos\(\mu_{0}\) por\(\mu\). En materiales diamagnéticos, donde la susceptibilidad es negativa, tenemos eso\(\mu_{r} < 1, \: \mu < \mu_{0}\). Sin embargo, sustituyendo en nuestros valores típicos

\[\chi_{m} = - \frac{Ne^{2}\mu_{0}R^{2}}{2 m.} \approx \frac{4.4 \times 10^{-35}}{Z^{2}}N \nonumber \]

vemos que incluso con\(N \approx 10^{30}\) átomos/m ³,\(\chi_{m}\) es mucho menor que la unidad por lo que los efectos diamagnéticos son muy pequeños.

b) Paramagnetismo

En cuanto a la polarización de orientación, un campo magnético aplicado ejerce un par en cada dipolo tendiendo a alinear su momento con el campo, como se ilustra para el dipolo magnético rectangular con momento en ángulo\(\theta\) con un campo magnético uniforme B en la Figura 5-18a. La fuerza en cada pierna es

\[\textbf{df}_{1} = - \textbf{df}_{2} = I \Delta x \: \Delta x \: \textbf{i}_{x} \times \textbf{B} = I \: \Delta x[B_{y} \textbf{i}_{z} - B_{z} \textbf{i}_{y}] \\ \textbf{df}_{3} = - \textbf{df}_{4} = I \: \Delta y \: \textbf{i}_{y} \times \textbf{B} = I \: \Delta y (-B_{x} \textbf{i}_{z} + B_{z} \textbf{i}_{x}) \nonumber \]

En un campo magnético uniforme, las fuerzas sobre patas opuestas son iguales en magnitud pero opuestas en dirección para que la red

Figura 5-18 (a) Se ejerce un par sobre un dipolo magnético con momento en ángulo\(\theta\) con un campo magnético aplicado. (b) A partir de las estadísticas de Boltzmann, la agitación térmica se opone a la alineación de dipolos magnéticos. Todos los dipolos en ángulo\(\theta\), juntos tienen una magnetización neta en la dirección del campo aplicado.

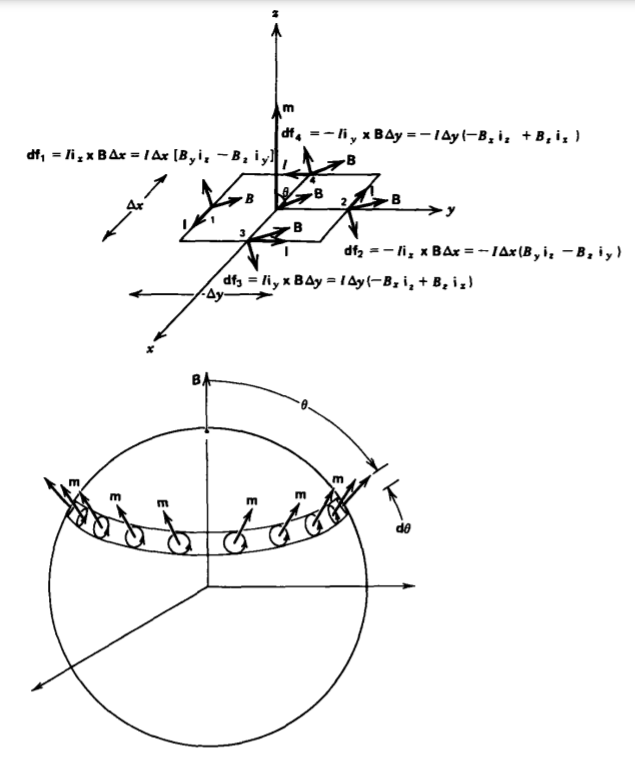
la fuerza en el bucle es cero. Sin embargo, hay un par:

\[\textbf{T} = \sum_{n=1}^{4} \textbf{r} \times \textbf{df}_{n} \\ = \frac{\Delta y}{2} (- \textbf{i}_{y} \times \textbf{df}_{1} + \textbf{i}_{y} \times \textbf{df}_{2}) + \frac{\Delta x}{2} (\textbf{i}_{x} \times \textbf{df}_{3} - \textbf{i}_{x} \times \textbf{df}_{4}) \\ = I \Delta x \: \Delta y (B_{x}i_{y} - B_{y}\textbf{i}_{x}) = \textbf{m} \times \textbf{B} \nonumber \]

La cantidad incremental de trabajo necesario para girar el dipolo en un ángulo pequeño\(d \theta\) es

\[dW = T \: d \theta = m \mu_{0} H_{0} \sin \theta d \theta \nonumber \]

de manera que la cantidad total de trabajo necesaria para girar el dipolo de\(\theta = 0\) a cualquier valor de\(\theta\) es

\[W = \int_{0}^{\theta} T \: d \theta = - m \mu_{0} H_{0} \cos \theta \big|_{0}^{\theta} = m \mu_{0} H_{0} (1-\cos \theta) \nonumber \]

Esta obra se almacena como energía potencial, pues si se libera el dipolo intentará orientarse con su momento paralelo al campo. La agitación térmica se opone a esta alineación donde la estadística de Boltzmann describe la densidad numérica de dipolos que tienen energía W como

\[n = n_{1} e^{-W/kT} = n_{1} e^{-m \mu_{0} H_{0} (1-\cos \theta)/kT} = n_{0} e^{m \mu_{0} H_{0} \cos \theta/ kT} \nonumber \]

donde agrupamos la contribución de energía constante en (40) dentro de la amplitud\(n_{0}\), que se encuentra especificando la densidad numérica promedio de los dipolos N dentro de una esfera de radio R:

\[N = \frac{1}{\frac{4}{3} \pi R^{3}} \int_{\theta = 0}^{\pi} \int_{\phi = 0}^{2 \pi} \int_{r = 0 }^{R} n_{0} e^{a \cos \theta} r^{2} \sin \theta dr \: d \theta \: d \phi \\ = \frac{n_{0}}{2} \int_{\theta = 0}^{\pi} \sin \theta e^{a \cos theta} d \theta \nonumber \]

donde dejamos

\[a = m \mu_{0} H_{0}/kT \nonumber \]

Con el cambio de variable

\[u = a \cos \theta, \: \: \: \: du = -a \sin \theta \: d \theta \nonumber \]

la integración en (42) se convierte

\[N = \frac{-n_{0}}{2a} \int_{a}^{-a} e^{u} du = \frac{n_{0}}{a} \sinh a \nonumber \]

para que (41) se convierta

\[n = \frac{N_{a}}{\sinh a} e^{a \cos \theta} \nonumber \]

De la Figura 5-18b vemos que todos los dipolos en el caparazón\(\theta\) a lo largo del intervalo para\(\theta + d \theta\) contribuir a una magnetización neta. que está en la dirección del campo magnético aplicado:

\[dM = \frac{mn}{\frac{4}{3} \pi R^{3}} \cos \theta r^{2} \sin \theta \: dr \: d \theta \: d \phi \nonumber \]

de manera que la magnetización total debida a todos los dipolos dentro de la esfera es

\[M = \frac{maN}{2 \sinh a} \int_{\theta = 0}^{\pi} \sin \theta \cos \theta e^{a \cos \theta} d \theta \nonumber \]

Nuevamente utilizando el cambio de variable en (44), (48) se integra a

\[M = \frac{-mN}{2a \sinh a} \int_{a}^{-a} u e^{u} du \\ = \frac{-m N}{2a \sinh a} e^{u} (u-1) \big|_{a}^{a} \\ = \frac{-mN}{2a \sinh a} [e^{-a} (-a -1) - e^{a} (a-1)] \\ = \frac{-mN}{a \sinh a} [-a \cosh a + \sinh a] \\ = mN[\coth a -1/a] \nonumber \]

que se conoce como la ecuación de Langevin y se representa en función de la temperatura recíproca en la Figura 5-19. A bajas temperaturas (alta a) la magnetización se satura a M = mN ya que todos los dipolos tienen sus momentos alineados con el campo. A temperatura ambiente, a suele ser muy pequeño. Usando los parámetros en (26) y (27) en un campo magnético fuerte de\(H_{0} = 10^{6}\) amps/m, a es mucho menor que la unidad:

\[a = \frac{m \mu_{0}H_{0}}{kT} = \frac{e \omega}{2} R^{2} \frac{\mu_{0}H_{0}}{kT} \approx 8 \times 10^{-4} \nonumber \]

Figura 5-19 La ecuación de Langevin describe la magnetización neta. A bajas temperaturas (alta a) todos los dipolos se alinean con el campo provocando saturación. A altas temperaturas (a << 1) la magnetización aumenta linealmente con el campo.

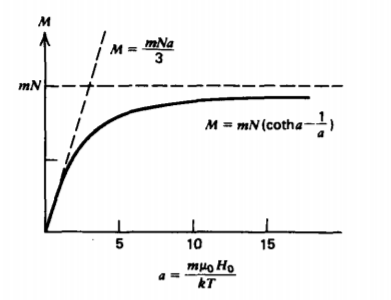
En este límite, la ecuación de Langevin simplifica a

\[\lim_{a << 1}M \approx mN \bigg[ \frac{1 + a^{2}/2}{a + a^{3}/6} - \frac{1}{a} \bigg] \\ \approx mN \bigg( \frac{(1 + a^{2}/2)(1-a^{3}/6)}{a} = \frac{1}{a} \bigg] \\ \approx \frac{mNa}{3} \approx \frac{\mu_{0}m^{2}N}{3kT}H_{0} \nonumber \]

En este límite la susceptibilidad magnética\(\chi_{m}\) es positiva:

\[\textbf{M} = \chi_{m}\textbf{H}, \: \: \: \chi_{m} = \frac{\mu_{0}m^{2}N}{3 kT} \nonumber \]

pero incluso con\(N \approx 10^{30}\) átomos/m ³, sigue siendo muy pequeño:

\[\chi_{m} \approx 7 \times 10^{-4} \nonumber \]

c) Ferromagnetismo

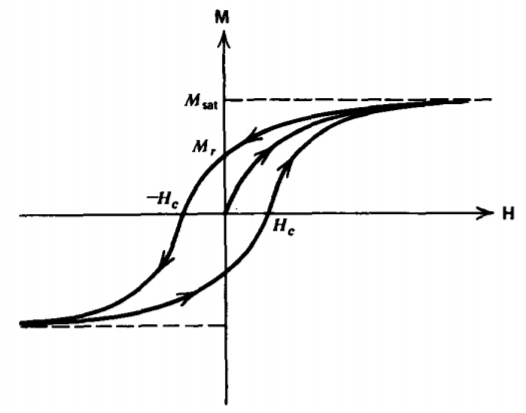
En cuanto a los ferroeléctricos (ver Sección 3-1-5), el acoplamiento suficientemente alto entre dipolos magnéticos adyacentes en algunas aleaciones de hierro hace que se alineen espontáneamente incluso en ausencia de un campo magnético aplicado. Cada uno de estos dominios microscópicos actúan como un imán permanente, pero se distribuyen aleatoriamente por todo el material para que la magnetización macroscópica sea cero. Cuando se aplica un campo magnético, los dipolos tienden a alinearse con el campo para que los dominios con una magnetización a lo largo del campo crezcan a expensas de los dominios no alineados.

El comportamiento similar a la fricción del movimiento de la pared del dominio es un proceso con pérdida de manera que la magnetización varía con el campo magnético de manera no lineal, como lo describe el bucle de histéresis en la Figura 5-20. Un campo fuerte alinea todos los dominios con la saturación. Al disminuir H, la magnetización va a la zaga de manera que existe una magnetización remanente _Mr incluso con campo cero. En esta condición tenemos un imán permanente. Para llevar la magnetización a cero se requiere un campo coercitivo negativo - H _c.

Aunque no lineal, la principal importancia de ingeniería de los materiales ferromagnéticos es que la permeabilidad relativa\(\mu_{r}\) suele ser de miles:

\[\mu = \mu_{r} \mu_{0} = \textbf{B}/\textbf{H} \nonumber \]

Este valor suele ser tan alto que en aplicaciones de ingeniería lo idealizamos para que sea infinito. En este límite

\[\lim_{\mu \rightarrow \infty} \textbf{B} = \mu \textbf{H} \Rightarrow \textbf{H} = 0, \: \: \: \: \textbf{B} \: \textrm{ finite} \nonumber \]

el campo H se convierte en cero para mantener el campo B finito.

Figura 5-20 Los materiales ferromagnéticos exhiben histéresis donde la magnetización se satura a altas intensidades de campo y retiene una magnetización remanente neta _Mr incluso cuando H es cero. Se requiere un campo coercitivo - H _c para que la magnetización vuelva a cero.

Ejemplo 5-1: Corriente de línea infinita dentro de un cilindro magnéticamente permeable

Una corriente de línea I de extensión infinita se encuentra dentro de un cilindro de radio a que tiene permeabilidad\(\mu\), como en la Figura 5-21. El cilindro está rodeado de espacio libre. ¿Cuáles son los campos B, H y M en todas partes? ¿Cuál es la corriente de magnetización?

Figura 5-21 Una corriente de línea libre de extensión infinita colocada dentro de un cilindro permeable da lugar a una corriente de magnetización de línea a lo largo del eje y una corriente de magnetización superficial dirigida opuestamente en la superficie del cilindro.

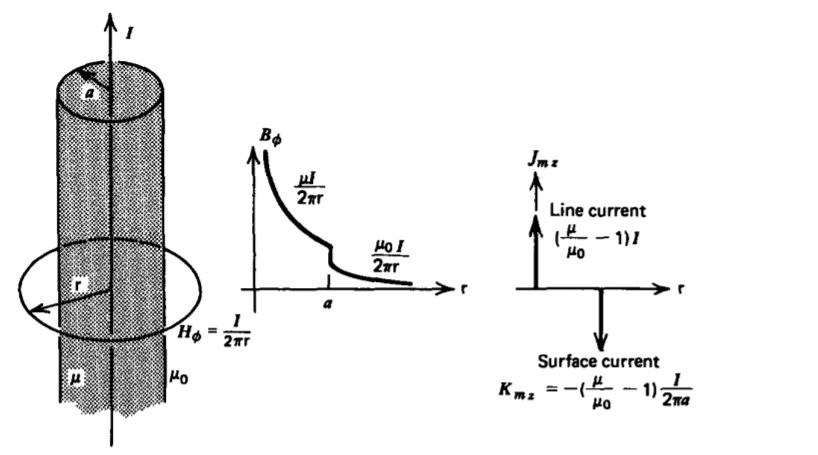
Solución

Elija un contorno circular de radio r alrededor de la corriente. Utilizando la forma integral de la ley de Ampere, (21), el campo H es de la misma forma ya sea dentro o fuera del cilindro:

\(\oint_{L} \textbf{H} \cdot \textbf{dl} = H_{\phi} 2 \pi \textrm{r} = I \Rightarrow H_{\phi} = \frac{I}{2 \pi \textrm{r}}\)

La densidad de flujo magnético difiere en cada región porque la permeabilidad difiere:

\(B_{\phi} = \left \{ \begin{matrix} \mu H_{\phi} = \frac{\mu I}{2 \pi \textrm{r}}, & 0 < \textrm{r} < a \\ \mu_{0} H_{\phi} = \frac{\mu_{0}I}{2 \pi \textrm{r}}, & \textrm{r} > a \end{matrix} \right.\)

La magnetización se obtiene de la relación

\(\textbf{M} = \frac{\textbf{B}}{\mu_{0}} - \textbf{H}\)

como

\[M_{\phi} = \left \{ \begin{matrix} \bigg(\frac{\mu}{\mu_{0}} - 1 \bigg) H_{\phi} = \frac{\mu - \mu_{0}}{\mu_{0}} \frac{I}{2 \pi \textrm{r}}, & 0 < \textrm{r} < a \\ 0, & \textrm{r} > a \end{matrix} \right. \nonumber \]

La corriente de magnetización volumétrica se puede encontrar usando (16):

\[\textbf{J}_{m} = \nabla \times \textbf{M} = - \frac{\partial M_{\phi}}{\partial z} \textbf{i}_{\textrm{r}} + \frac{1}{r} \frac{\partial}{\partial textrm{r}}( \textrm{r} M_{\phi}) \textbf{i}_{z} = 0, \: \: \: \: 0 < \textrm{r} < a \nonumber \]

No hay corriente de magnetización masiva porque no hay corrientes libres a granel. Sin embargo, hay una corriente de magnetización de línea a r =0 y una corriente de magnetización superficial a r = a. Se encuentran fácilmente usando la forma integral de (16) del teorema de Stokes:

\[\int_{S} \nabla \times \textbf{M} \cdot \textbf{dS} = \oint_{L} \textbf{M} \cdot \textbf{dl} = \int_{S} \textbf{J}_{m} \cdot \textbf{dS} \nonumber \]

Escoja un cortour alrededor del centro del cilindro con r < a

\[M_{\phi} 2 \pi \textrm{r} = \bigg( \frac{\mu - \mu_{0}}{\mu_{0}} \bigg) I = I_{m} \nonumber \]

donde\(I_{m}\) está la corriente de la línea de magnetización. El resultado permanece sin cambios para cualquier radio r< a ya que no se encierra más corriente ya que\(\textbf{J}_{m} = 0 \) para 0 < r < a. Tan pronto como r > a,\(M_{\phi}\) se convierte en cero para que la corriente de magnetización total se convierta en cero. Por lo tanto, a r = a una corriente de magnetización superficial debe fluir cuya corriente total es igual en magnitud pero opuesta en signo a la corriente de magnetización de línea:

\[K_{zm} = \frac{-I_{m}}{2 \pi a} = - \frac{\mu - \mu_{0})I}{\mu_{0} 2 \pi a} \nonumber \]