5.9: Problemas
- Page ID
- 86869
Sección 5-1
Una carga\(q\) de masa\(m\) se mueve a través de un campo magnético uniforme\(B_{0} \textbf{i}_{z}\). A\( t =0\) su velocidad y desplazamiento son
\(\textbf{v} (t = 0) = v_{x0} \textbf{i}_{x} + v_{y0} \textbf{i}_{y} + v_{z0} \textbf{i}_{z} \\ \textbf{r}(t = 0) = x_{0} \textbf{i}_{x} + y_{0} \textbf{i}_{y} + z_{0} \textbf{i}_{z}\)
a) ¿Cuál es la velocidad y desplazamiento posteriores?
(b) Demostrar que su movimiento proyectado sobre el\(xy\) plano es un círculo. ¿Cuál es el radio de este círculo y dónde está su centro?
c) ¿Cuál es la dependencia temporal de la energía cinética de la carga\(\frac{1}{2} m \vert \textbf{v} \vert ^{2}\)?
Un magnetrón es esencialmente un condensador de placa paralela estresado por voltaje constante\(V_{0}\) donde los electrones de carga\( -e\) se emiten a\(x = 0, \,y = 0\) una velocidad inicial cero. Se aplica un campo\(B_{0} \textbf{i}_{z}\) magnético transversal. Descuidar los campos eléctricos y magnéticos debidos a los electrones en comparación con el campo aplicado.
(a) ¿Cuál es la velocidad y desplazamiento de un electrón, inyectado con velocidad inicial cero a \(t = 0\)?
(b) ¿Qué valor del campo magnético sólo impedirá que los electrones lleguen al otro electrodo? Este es el campo magnético de corte.
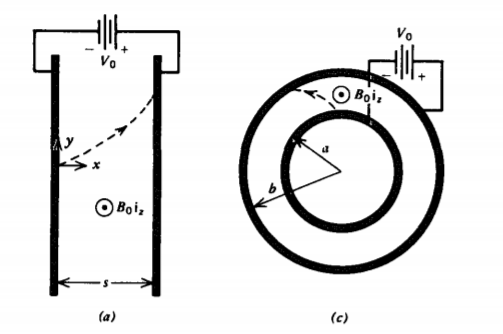
(c) Se construye un magnetrón con electrodos coaxiales desde donde se inyectan electrones\(r = a, \,\phi=0\) con velocidad inicial cero. Usando las relaciones de la Tabla 1-2,
\(\textbf{i}_{\textrm{r}} = \cos \phi \textbf{i}_{x} + \sin \phi \textbf{i}_{y} \\ \textbf{i}_{\phi} = - \sin \phi \textbf{i}_{x} + \cos \phi \textbf{i}_{y}\)
demuestre que
\(\frac{d \textbf{i}_{\textrm{r}}}{dt} = \textbf{i}_{\phi} \frac{d \phi}{d t} = \frac{v_{\phi}}{\textrm{r}} \textbf{i}_{\phi} \\ \frac{d \textbf{i}_{\phi}}{dt} = - \textbf{i}_{\textrm{r}} \frac{d \phi}{dt} = - \frac{v_{\phi}}{\textrm{r}} \textbf{i}_{\textrm{r}}\)
¿Cuál es la aceleración de una carga con velocidad?
\(\textbf{v} = v_{\textrm{r}} \textbf{i}_{\textrm{r}} + v_{\phi} \textbf{i}_{\phi}\)?
(d) Encontrar la velocidad de los electrones en función de la posición radial.
Pista:
\(\frac{dv_{\textrm{r}}}{dt} = \frac{dv_{\textrm{r}}}{d \textrm{r}} \frac{d \textrm{r}}{dt} = v_{\textrm{r}} \frac{dv_{\textrm{r}}}{d \textrm{r}} = \frac{d}{d \textrm{r}} (\frac{1}{2} v_{\textrm{r}}^{2}) \\ \frac{dv_{\phi}}{dt} = \frac{dv_{\phi}}{d \textrm{r}} \frac{d \textrm{r}}{dt} = v_{\textrm{r}} \frac{dv_{\phi}}{d \textrm{r}} \)
e) ¿Cuál es el campo magnético de corte? Consulta tu respuesta con (b) en el límite\(b = a +s \) donde\(s\ll a\).
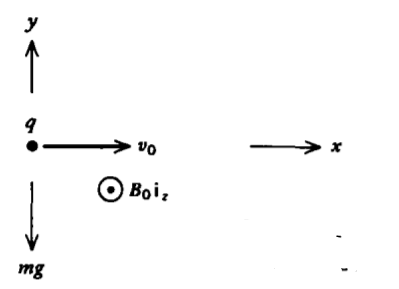
Una carga\(q\) de masa\(m\) dentro de un campo de gravedad\(-g\textbf{i}_{y}\) tiene una velocidad inicial\(v_{0} \textbf{i}_{x}\). Se aplica un campo\(B_{0} \textbf{i}_{z}\) magnético. ¿Qué valor de\(B_{0}\) mantendrá la partícula moviéndose a velocidad constante en la\(x\) dirección?
La relación carga/masa de un electrón\(e/m\) se midió primero por Sir J. J. Thomson en\(1897\) el dispositivo de tubo de rayos catódicos mostrado. Los electrones emitidos por el cátodo pasan a través de una hendidura en el ánodo hacia una región con campos eléctricos y magnéticos cruzados, siendo ambos perpendiculares a la velocidad de los electrones. El extremo del tubo está recubierto con un material fluorescente que produce un punto brillante donde impacta el haz de electrones.
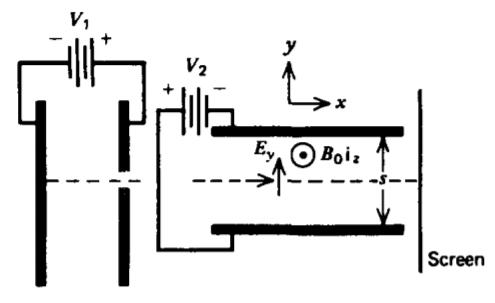
(a) ¿Cuál es la velocidad de los electrones al pasar por la hendidura si su velocidad inicial del cátodo es\(v_{0}\)?
b) El campo eléctrico\(\textbf{E}\) y el campo magnético \(\textbf{B}\)se ajustan para que la deflexión vertical del haz sea cero. ¿Cuál es la velocidad inicial del electrón? (Negligencia gravedad.)
(c) El voltaje\(V_{2}\) se establece ahora en cero. ¿Cuál es el radio\(R\) del movimiento de los electrones sobre el campo magnético?
d) ¿Qué es\(e/m\) en términos de\(E\)\(B\), y\(R\)?
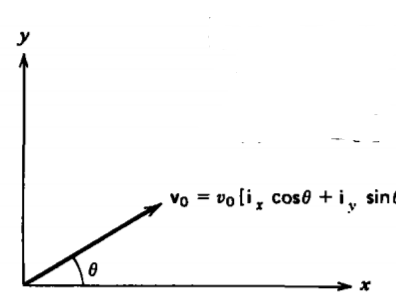
Una carga\(q\) de masa\(m\) en\(t = 0\) cruza el origen con velocidad\(\textbf{v}_{0} = \textbf{v}_{x0} \textbf{i}_{x} + v_{y 0} \textbf{i}_{y}\). Para cada uno de los siguientes campos magnéticos aplicados, ¿dónde y cuándo vuelve a cruzar el\(y =0\) avión la carga?
(a)\(\textbf{B} = B_{0} \textbf{i}_{x}\)
b)\(\textbf{B} = B_{0} \textbf{i}_{y}\)
c)\(\textbf{B} = B_{0} \textbf{i}_{z}\)
En 1896 Zeeman observó que un átomo en un campo magnético tenía una división fina de sus líneas espectrales. Una teoría clásica del efecto Zeeman, desarrollada por Lorentz, modeló el electrón con masa\(m\) como unido al núcleo por una fuerza de resorte con constante de resorte de\(k\) modo que en ausencia de un campo magnético su frecuencia natural era\(\omega_{k} = \sqrt{k/m}\)
(a) Se\(B_{0}\textbf{i}_{z}\) aplica un campo magnético. Escribe la ley de Newton para el\(x\),\(y\), y\(z\) los desplazamientos del electrón incluyendo la primavera y las fuerzas de Lorentz.
(b) Debido a que estas ecuaciones son lineales, adivina soluciones exponenciales de la forma\(e^{st}\). ¿Cuáles son las frecuencias naturales?
(c) Debido a que normalmente\(\omega_{k}\) se encuentra en el rango óptico (\(\omega_{k} \approx 10^{15}\)radián/seg), muestran que la división de frecuencia es pequeña en comparación con\(\omega_{k}\) incluso para un campo fuerte de\(B_{0}\) = 1 tesla. En este límite, encuentra expresiones aproximadas para las frecuencias naturales de (b).
Una carga\(q\) se mueve a través de una región donde hay un campo eléctrico\(\textbf{E}\) E y un campo magnético\(\textbf{E}\) B. El medio es muy viscoso por lo que los efectos inerciales son insignificantes,
\(\beta \textbf{v} = q (\textbf{E} + \textbf{v} \times \textbf{B})\)
donde\(\beta\) está el coeficiente de arrastre viscoso. ¿Cuál es la velocidad de la carga? (Pista:\(\textbf{v} \times \textbf{B} = - \textbf{v} (\textbf{B} \cdot \textbf{B}) + \textbf{B}(\textbf{v} \cdot \textbf{B})\) y\(\textbf{v} \cdot \textbf{B} = (q/\beta) \textbf{E} \cdot \textbf{B}.\))
Las cargas de masa\(m\)\(q\), carga y densidad numérica\(n\) se mueven a través de un material conductor y chocan con el medio anfitrión con una frecuencia de colisión\(\nu\) en presencia de un campo eléctrico \(\textbf{E}\)y un campo magnético\(\textbf{B}\).
a) Escribir la primera ley de Newton para los transportistas de carga, en la misma línea que se desarrolló en la Sección 3-2-2, con la adición de la fuerza Lorentz.
b) Descuidar la inercia y difusión de las partículas, resolver la velocidad de las partículas\(\textbf{v}\).
c) ¿Cuál es la ley constitutiva que relaciona la densidad\(\textbf{J}=qn\textbf{v}\) de corriente con \(\textbf{E}\)y\(\textbf{B}\). Esta es la ley generalizada de Ohm en presencia de un campo magnético.
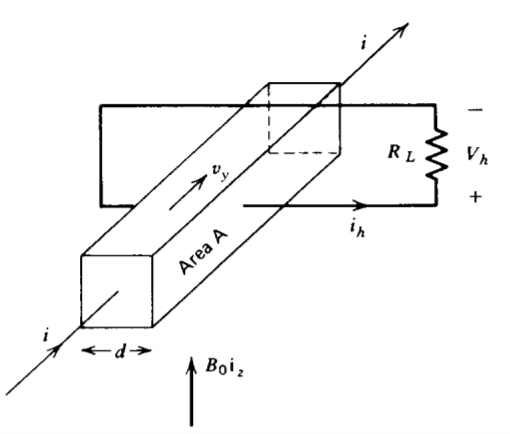
d) ¿Qué es la conductividad óhmica\(\sigma\)? \(i\)Se pasa una corriente a través de este material en presencia de un campo magnético perpendicular. Una resistencia\(R_{L}\) está conectada a través de los terminales. ¿Cuál es el voltaje Hall? (Ver parte superior de la página 379).
e) ¿Qué valor de\(R_{L}\) maximiza la potencia disipada en la carga?
Sección 5-2
Una carga\(q\) puntual viaja dentro del campo magnético de una corriente de línea infinitamente larga\(I\). A\(r = r0\) su velocidad es
\(\textbf{v} (t = 0) = v_{r0} \textbf{i}_{\textrm{r}} + v_{\phi 0} \textbf{i}_{\phi} + v_{z0} \textbf{i}_{z}\)
Su velocidad posterior es sólo una función de\(r\).
a) ¿Cuál es la velocidad de la carga en función de la posición? Pista: Ver Problema 2c y 2d,
\( \int \frac{\ln x}{x} dx = \frac{1}{2} (\ln x)^{2}\)
b) ¿Cuál es la energía cinética de la carga?
c) ¿Cuál es la distancia más cercana a la que la carga puede acercarse a la corriente de línea si\(v_{\phi 0} = 0 \)?
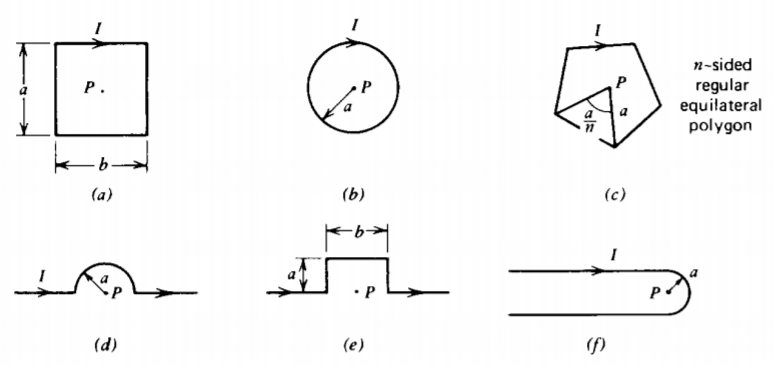
Encuentre el campo magnético en el punto P que se muestra para las siguientes corrientes de línea:
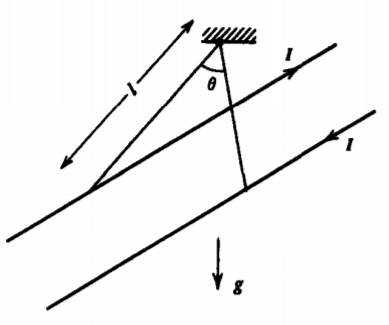
Dos corrientes largas de línea paralela de masa por unidad de longitud\(m\) en un campo \(g\)de gravedad transportan una corriente\(I\) en direcciones opuestas. Están suspendidos por cordones de longitud\(l\). ¿Cuál es el ángulo\(\theta\) entre los cordones?
Una corriente constante\(K_{0} \textbf{i}_{\phi}\) fluye sobre la superficie de una esfera de radio\(R\).
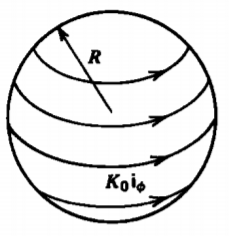
a) ¿Cuál es el campo magnético en el centro de la esfera? (CONSEJO:\(\textbf{i}_{\phi} \times \textbf{i}_{r} = \textbf{i}_{\phi} = \cos \theta \cos \phi \textbf{i}_{x} + \cos \theta \sin \phi \textbf{i}_{y} - \sin \theta \textbf{i}_{z}\).)
(b) Utilizar los resultados de (a) para encontrar el campo magnético en el centro de una concha esférica de radio interior\(R_1\) y radio exterior\(R_2\) que transporta una corriente volumétrica uniformemente distribuida\(J_{0} \textbf{i}_{\phi}\).
Una corriente\(I\) de línea de longitud\(2L\) fluye a lo largo del \(z\)eje.
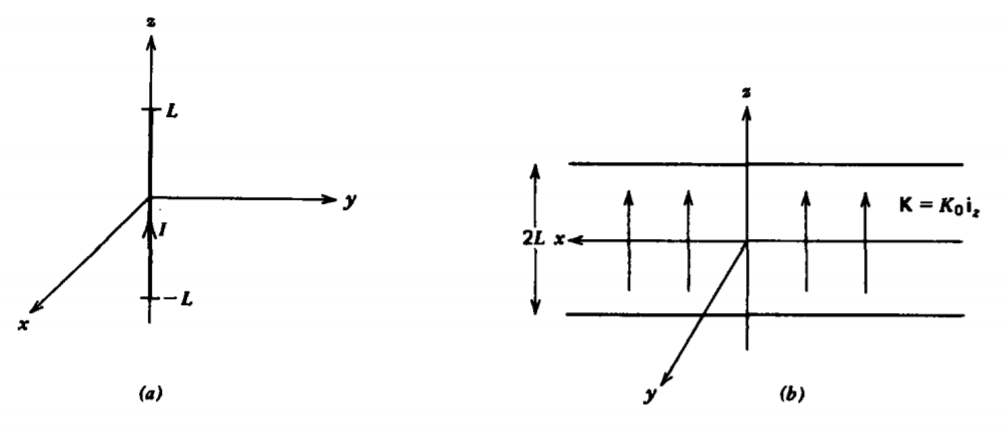
a) ¿Cuál es el campo magnético en todas partes del\(z =0\) avión?
(b) Utilizar los resultados de (a) para encontrar el campo magnético en el\(z = 0\) plano debido a una hoja de corriente infinitamente larga de altura\(2L\) y densidad de corriente uniforme\(K_{0}\textbf{i}_{z}\). Pista: Let\(u=x^{2} + y^{2}\)
\(\int \frac{du}{u(u^{2} + bu - a)^{1/2}} = \frac{1}{\sqrt{a}} \sin^{-1} \bigg( \frac{bu + 2a}{u \sqrt{b^{2} + 4a}} \bigg) \)
Los alambres estrechamente espaciados se enrollan alrededor de un núcleo cilíndrico infinitamente largo en ángulo de paso\(\theta_{0}\). Una corriente que fluye en los cables se aproxima luego a una corriente de superficie
\(\textbf{K} = K_{0} (\textbf{i}_{z} \sin \theta_{0} + \textbf{i}_{\phi} \cos \theta_{0})\)
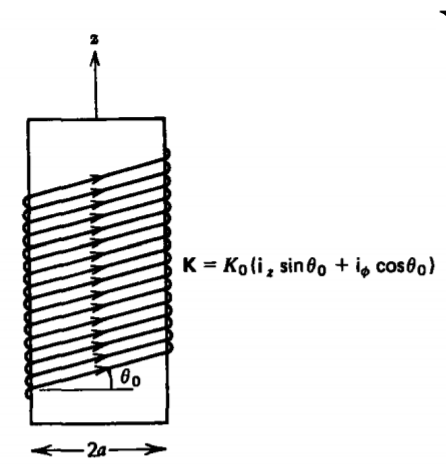
¿Cuál es el campo magnético en todas partes?
Una losa infinita lleva una corriente uniforme\(J_{0}\textbf{i}_{z}\) excepto dentro de un agujero cilíndrico de radio \(a\)centrado dentro de la losa.
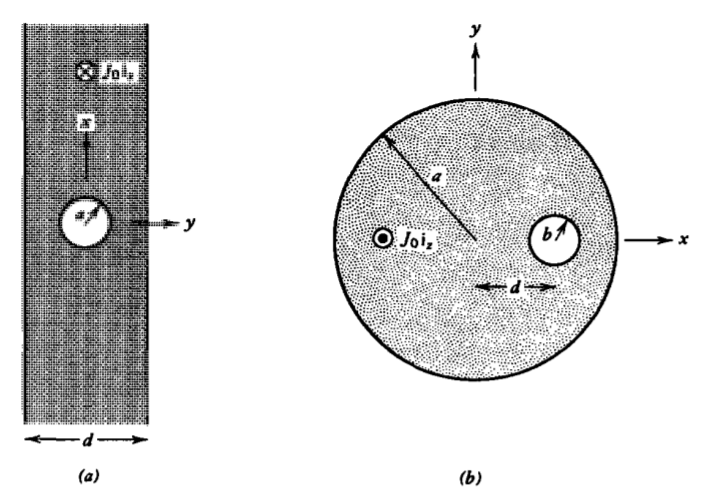
(a) ¿Encuentra el campo magnético en todas partes? (Pista: Use superposición reemplazando el agujero por dos corrientes opuestas).
(b) Un cilindro infinitamente largo de radio\(a\) que transporta una corriente uniforme\(J_{0}\textbf{i}_{z}\) tiene un orificio de radio fuera del eje\(b\) con centro a una\(d\) distancia del centro del cilindro. ¿Cuál es el campo magnético dentro del agujero? (Pista: Convertir a coordenadas cartesianas\(\textrm{r} \textbf{i}_{\phi} = x \textbf{i}_{y}- y \textbf{i}_{x}\))
Sección 5.3
¿Cuál de los siguientes vectores puede ser un campo magnético\(\textbf{B}\)? Si es así, ¿cuál es la densidad de corriente\(\textbf{J}\)?
(a)\(\textbf{B} = a r \textbf{i}_{r}\)
b)\(\textbf{B} = a (x \textbf{i}_{y} - y \textbf{i}_{x})\)
c)\(\textbf{B} = a (x \textbf{i}_{x} - y \textbf{i}_{y})\)
d)\(\textbf{B} = a \textrm{r} \textbf{i}_{\phi}\)
Encuentre el campo magnético en todas partes para cada una de las siguientes distribuciones de corriente:
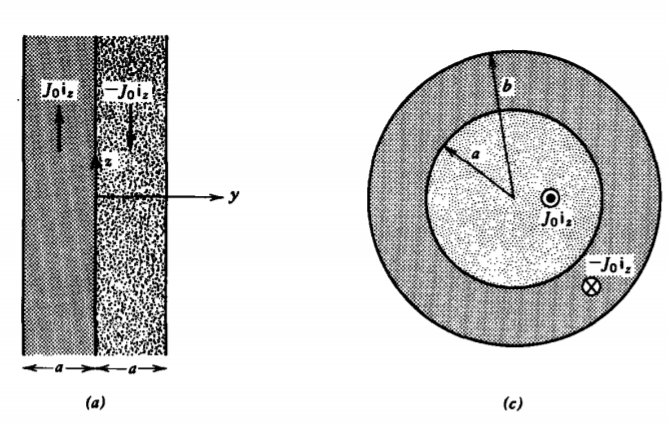
(a)\(\textbf{J} = \left \{ \begin{matrix} J_{0} \textbf{i}_{z}, & -a < y < 0 \\ -J_{0}\textbf{i}_{z,} & 0 < y < a \end{matrix} \right. \)
b)\(\textbf{J} = \frac{J_{0}y}{a} \textbf{i}_{z}, \: \: \: \: -a < y < a \)
c)\(\textbf{J} = \left \{ \begin{matrix} J_{0}\textbf{i}_{z}, & 0 < \textrm{r} < a \\ -J_{0} \textbf{i}_{z}, & a < \textrm{r} < b \end{matrix} \right. \)
d)\(\textbf{J} = \left \{ \begin{matrix} \frac{J_{0} \textrm{r}}{a} \textbf{i}_{z}, & \textrm{r} < a \\ 0, & \textrm{r} > a \end{matrix} \right. \)
Sección 5.4
Dos hojas de corriente semiinfinitas paralelas a una distancia de\(d\) distancia tienen sus corrientes fluyendo en direcciones opuestas y se extienden a lo largo del intervalo\( - \infty < x < 0\).
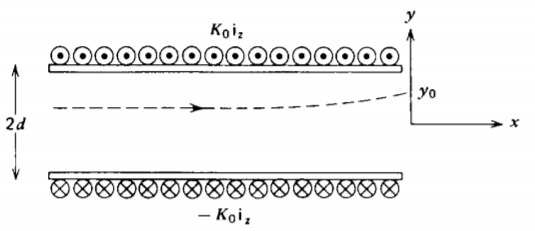
a) ¿Cuál es el potencial vectorial? (Pista: Usar superposición de los resultados en la Sección 5-3-4b.)
b) ¿Cuál es el campo magnético en todas partes?
c) ¿Cuánto flujo magnético por unidad de longitud emana a través de la cara abierta\(x = 0\)? ¿Cuánto flujo magnético por unidad de longitud pasa a través de cada hoja de corriente?
d) Una línea de campo magnético emana en la posición\(y_{0} (0 < y_{0} < d)\) del\(x = 0\) plano. ¿A qué valor de\(y\) está esta línea de campo\(x = - \infty\)?
(a) Demostrar que\(\nabla \cdot \textbf{A} \neq 0\) para la línea de longitud finita corriente en la Sección 5-4-3a. ¿Por qué es así?
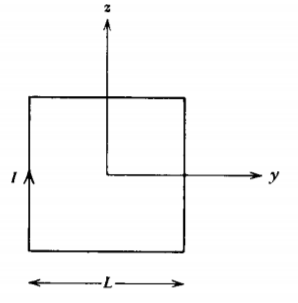
(b) Encontrar el potencial vectorial para un bucle cuadrado.
c) ¿Qué es\(\nabla \cdot \textbf{A}\) ahora?
Encuentre el potencial de vector magnético y el campo ma netico para las siguientes distribuciones actuales: (Pista:\(\nabla^{2} \textbf{A} = \nabla ( \nabla \cdot \textbf{A})\))
(i) Cilindro infinitamente largo de radio a que lleva un
(a) corriente superficial\(K_{0} \textbf{i}_{\phi}\)
b) corriente superficial,\(K_{0} \textbf{i}_{z}\)
(c) corriente de volumen\(J_{0}\textbf{i}_{z}\)
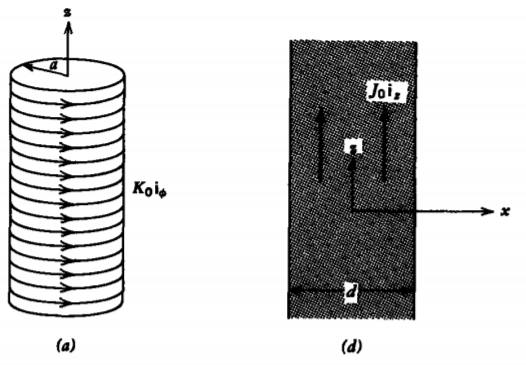
(ii) Losa infinitamente larga de espesor\(\) d que lleva a
d) corriente de volumen\(J_{0} \textbf{i}_{z}\)
e) corriente de volumen\(\frac{J_{0}x}{d} \textbf{i}_{z}\)
Sección 5.5
Una definición general para el momento dipolar magnético para cualquier bucle de corriente conformado es
\(\textbf{m} = \frac{1}{2} \oint \textbf{r} \times \textbf{I} dl\)
Si la corriente se distribuye sobre una superficie o volumen o se debe a una carga de punto móvil, utilizamos
\(\textbf{I} dl \rightarrow q \textbf{v} \rightarrow \textbf{K} d \textrm{S} \rightarrow \textbf{J} d \textrm{V}\)
Cuál es el momento dipolo magnético para las siguientes distribuciones de corriente:
a) una carga puntual q girada a velocidad angular constante\(\omega\) en el radio \(a\);
b) un bucle de corriente circular de radio a que lleve una corriente\(I\);
c) un disco de radio a con corriente superficial\(K_{0} \textbf{i}_{\phi}\);
d) una esfera uniformemente distribuida de carga superficial o volumétrica con carga total\(\mathcal{Q}\) y radio\(R\) rotando en la\(\phi\) dirección a velocidad angular constante\(\omega\). (Pista:\(\textbf{i}_{r} \times \textbf{i}_{\phi} = - \textbf{i}_{\theta} = - [ \cos \theta \cos \phi \textbf{i}_{x} + \cos \theta \sin \phi \textbf{i}_{y} - \sin \theta \textbf{i}_{z}]\))
Dos dipolos magnéticos de punto idénticos\(\textbf{m}\) con polarizabilidad magnética\(\alpha (\textbf{m} = \alpha \textbf{H})\) están\(a\) separados a lo largo del\(z\) eje. Se aplica un campo\(H_{0} \textbf{i}_{z}\) macroscópico.
a) ¿Cuál es el campo magnético local que actúa sobre cada dipolo?
b) ¿Cuál es la fuerza en cada dipolo?
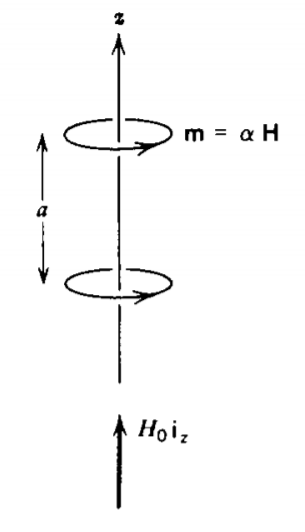
(c) Repetir (a) y (b) si tenemos una matriz infinita de tales dipolos. Pista:
\(\sum_{n=1}^{\infty} \frac{1}{n^{3}} \approx 1.2\)
d) Si asumimos que existe uno de esos dipolos dentro de cada volumen de\(a^{3}\), ¿cuál es la permeabilidad del medio?
Un electrón en órbita con momento magnético\(m_{z} \textbf{i}_{z}\) se encuentra en un campo magnético uniforme\(B_{0} \textbf{i}_{z}\) cuando en\(t = 0\) él está ligeramente desplazado de manera que su momento angular\(\textbf{L} = - (2m_{e}/e) \textbf{m}\) ahora también tiene componentes x e y.
(a) Demostrar que la ecuación de par puede ser puesta en términos del momento magnético
\(\frac{d \textbf{m}}{dt} = - \gamma \textbf{m} \times \textbf{B}\)
donde\(\gamma\) se llama la relación giromagnética. ¿Qué es\(\gamma\)?
(b) Escribir los tres componentes de (a) y resolver por el momento magnético si en \(t =0 \)este momento es inicialmente
\(\textbf{m} (t=0) = m_{x0} \textbf{i}_{x} + m_{y0} \textbf{i}_{y} + m_{z0} \textbf{i}_{z}\)
(c) Demostrar que el momento magnético precede sobre el campo magnético aplicado. ¿Cuál es la frecuencia de precesión?
Cuáles son los\(\textbf{M}\) campos\(\textbf{B}\)\(\textbf{H}\),, y y las corrientes de magnetización resultantes para los siguientes casos:
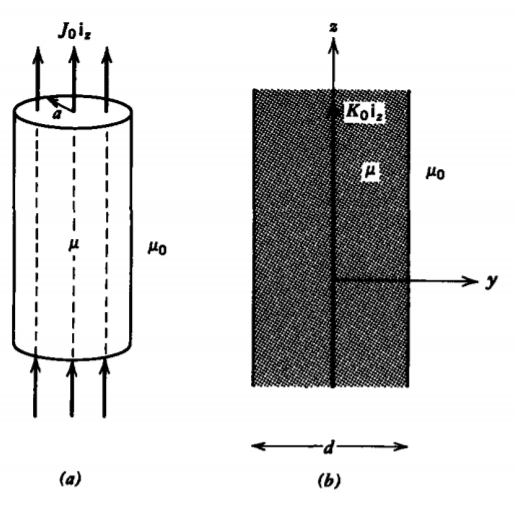
a) Una corriente volumétrica uniformemente distribuida\(J_{0}\textbf{i}_{z}\) a través de un cilindro de radio a y permeabilidad\(\mu\) rodeada de espacio libre.
(b) Una lámina actual\(K_{0} \textbf{i}_{z}\) centrada dentro de una losa permeable de espesor\(d\) rodeada de espacio libre.
Sección 5.6
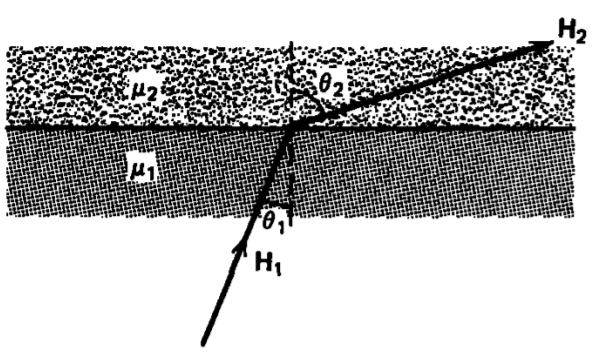
Un campo magnético con magnitud\(H_{1}\) incide sobre la interfaz plana que separa dos materiales linealmente permeables diferentes en un ángulo\(\theta_{1}\) de la normal. No hay corriente superficial en la interfaz. ¿Cuál es la magnitud y el ángulo del campo magnético en la región 2?
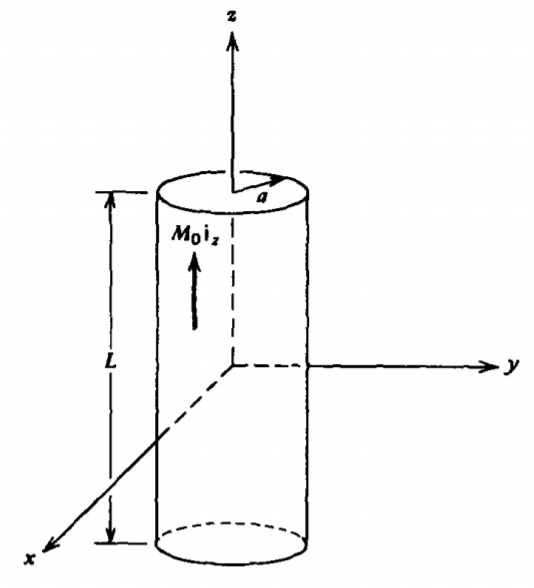
Un cilindro de radio a y longitud\(L\) está permanentemente magnetizado como\(M_{0}\textbf{i}_{z}\). \
a) ¿Cuáles son los\(\textbf{H}\) campos\(\textbf{B}\) y en todas partes a lo largo de su eje?
b) ¿Cuáles son los campos lejos del imán\(\left ( r\gg a,\,r\gg L \right )\)?
(c) Utilizar los resultados de (a) para encontrar los\(\textbf{H}\) campos\(\textbf{B}\) y en todas partes debido a una losa permanentemente magnetizada\(M_{0} \textbf{i}_{z}\) de\(xy\) extensión y grosor infinitos\(L\).
(d) Repetir (a) y (b) si el. cilindro tiene magnetización\(M_{0} (1-\textrm{r} /a) \textbf{i}_{z}\). Pista:
\(\int \frac{d \textrm{r}}{(a^{2} + \textrm{r}^{2})^{1/2}} = \ln (\textrm{r} + \sqrt{a^{2} + \textrm{r}^{2}})\)
Sección 5.7
Una corriente \(z\)de línea dirigida\(I\) es una distancia d por encima de la interfaz que separa dos materiales magnéticos diferentes con permeabilidades\(\mu_{1}\) y\(\mu_{2}\).

(a) Encontrar las corrientes de imagen\(I'\) en posición\(x =-d\) y\(I"\) en \(x=d\)esa satisfacer todas las condiciones de contorno. El campo en la región 1 se debe a\(I\) y\(I' \) mientras que el campo en la región 2 se debe a\(I"\). (Pista: Vea el problema dieléctrico análogo en la Sección 3-3-3.)
b) ¿Cuál es la fuerza por unidad de longitud en la corriente de línea\(I\)?
Una corriente de línea infinitamente larga\(I\) es paralela y está a una\(D\) distancia del eje de un cilindro de radio perfectamente conductor\(a\) que lleva una corriente superficial total\(I_{0}\).
(a) Encontrar corrientes de imagen adecuadas y verificar que se cumplan las condiciones de contorno. (Pista:\(x \textbf{i}_{y} - y \textbf{i}_{x} = \textrm{r} \textbf{i}_{\phi}; \: \: \: \textbf{i}_{y} = \sin \phi \textbf{i}_{\textrm{r}} + \cos \phi \textbf{i}_{\phi}; \: x = \textrm{r} \cos \phi.\))
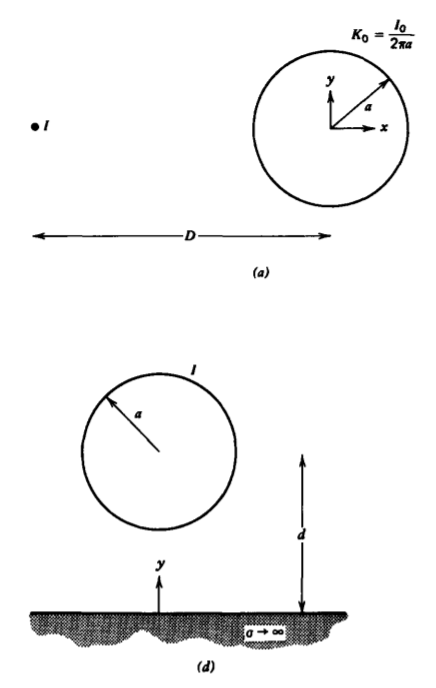
b) ¿Cuál es la distribución de corriente superficial en el cilindro? ¿Qué corriente total fluye en el cilindro? Pista:
\(\int \frac{d \phi}{a + b \cos \phi} = \frac{2}{[a^{2} - b^{2}]^{1/2}} \tan^{-1} \bigg( \frac{[a^{2} - b^{2}]^{1/2} \tan (\frac{1}{2} \phi)}{(a + b)} \bigg)\)
c) ¿Cuál es la fuerza por unidad de longitud sobre el cilindro?
(d) Un cilindro perfectamente conductor de radio a que transporta una corriente total \(I\)tiene su centro a una distancia\(d\) por encima de un plano perfectamente conductor. ¿Qué corrientes de imagen satisfacen las condiciones límite?
e) ¿Cuál es la fuerza por unidad de longitud sobre el cilindro?
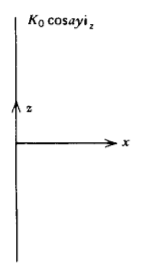
Se\(K_{0} \cos ay \textbf{i}_{z}\) coloca una hoja actual en\(x =0\). Debido a que no hay corrientes de volumen para\(x \neq 0\), se puede definir un potencial magnético escalar\(\textbf{H} = \nabla_{\chi}\).
a) ¿Para qué sirve la forma general de solución\(\chi\)? (Pista: Ver Sección 4-2-3.)
b) ¿Qué condiciones de frontera deben cumplirse?
c) ¿Cuál es el campo magnético y el potencial vectorial en todas partes?
d) ¿Cuál es la ecuación de las líneas del campo magnético?
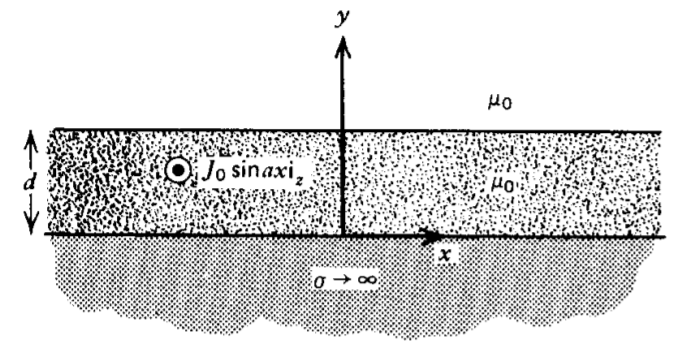
Una losa de espesor \(d\)lleva una distribución de corriente volumétrica\(J_{0} \sin a x \textbf{i}_{z}\) y se coloca sobre un plano de tierra perfectamente conductor.
(a) Encontrar una solución particular para el potencial del vector. ¿Se satisfacen todas las condiciones de contorno?
(b) Demostrar que se pueden agregar soluciones adicionales a las ecuaciones de Laplace al potencial vectorial para satisfacer las condiciones límite. ¿Cuál es el campo magnético en todas partes?
c) ¿Cuál es la distribución de la corriente superficial en el plano de tierra?
d) ¿Cuál es la fuerza por unidad de longitud sobre una sección de plano de tierra de ancho\(2 \pi/a\)? ¿Cuál es la fuerza corporal por unidad de longitud en una sección de la losa portadora actual de ancho\(2 \pi/a\)?
(e) Cuál es el campo magnético si la losa no lleva corriente pero está permanentemente magnetizada como\(M_{0} \sin ax \textbf{i}_{y}\) Repetir (c) y (d).
Una corriente de línea de longitud \(L\)se encuentra perpendicularmente sobre un plano de tierra perfectamente conductor.
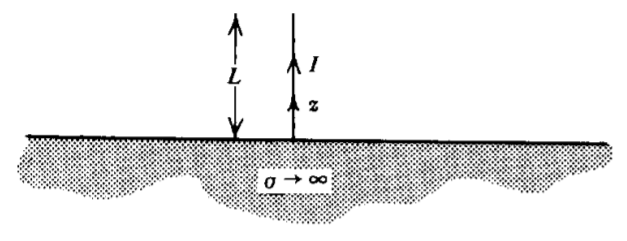
(a) Encontrar una corriente de imagen adecuada que sea equivalente a la corriente inducida en el\(z =0\) plano. ¿Te sorprende la dirección de la imagen actual?
b) ¿Cuál es el campo magnético en todas partes? (Pista: Ver Sección 5-4-3a.)
c) ¿Cuál es la distribución de corriente superficial en el plano conductor?
Un cilindro de radio a se coloca dentro de un campo magnético uniforme\(H_{0}\textbf{i}_{x}\) Encuentra el campo magnético para cada uno de los siguientes casos:
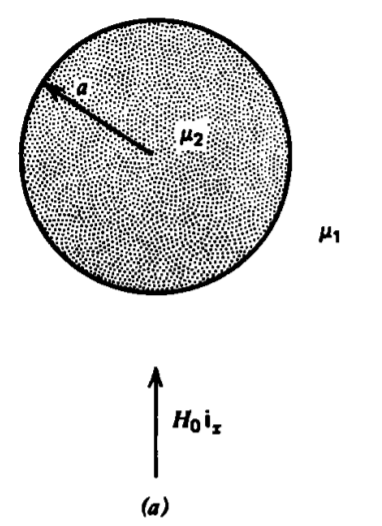
(a) El cilindro tiene permeabilidad\(\mu_{2}\) y el medio circundante tiene permeabilidad\(\mu_{1}\)
(b) Cilindro perfectamente conductor en espacio libre.
(c) Cilindro uniformemente magnetizado\(M_{2} \textbf{i}_{x}\) en un medio uniformemente magnetizado\(M_{1} \textbf{i}_{x}\).
Una hoja de corriente\(K_{0} \textbf{i}_{z}\) se coloca a lo largo del \(y\)eje\(x =0\) entre dos planos paralelos perfectamente conductores a una distancia de\(d\) distancia.
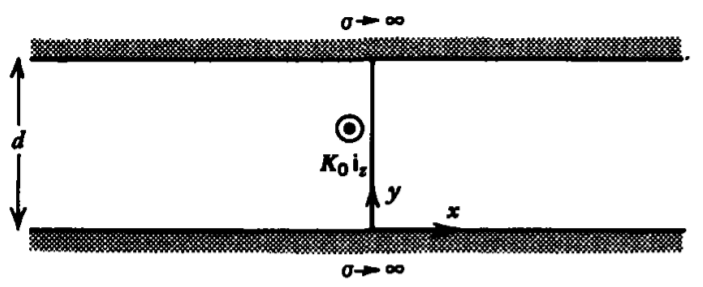
(a) Escribir la corriente constante en\(x =0\) como una serie infinita de Fourier de periodo fundamental\(2d\). (Pista: Ver Sección 4-2-5.)
b) ¿Qué forma general de potencial escalar\(\chi\), dónde\(\textbf{H} = \nabla_{\chi}\), satisfará las condiciones límite?
c) ¿Cuál es el campo magnético en todas partes?
d) ¿Cuál es la distribución de la corriente superficial y la corriente total en los planos conductores? Pista:
\(\sum_{n=1 \\ (n \textrm{ odd})}^{\infty} \frac{1}{n^{2}} = \frac{\pi^{2}}{8}\)
Sección 5.8
Un cilindro infinitamente largo de radio\(a\) está permanentemente magnetizado como\(M_{0} \textbf{i}_{x}\)
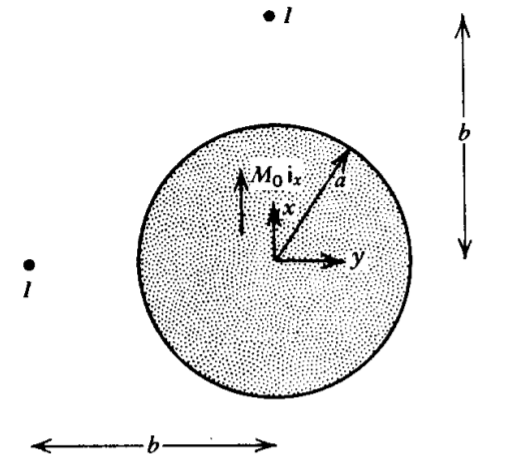
(a) Encontrar el campo magnético en todas partes.
(b) Una corriente de línea infinitamente larga\(I\) se coloca en\(y = -b\) o en \(x = b \,(b > a)\). Para cada uno de estos casos, ¿cuál es la fuerza por unidad de longitud en la línea actual? (Pista: Ver problema 32c.)
Los electrodos de placa paralela están separados por una losa conductora rectangular que tiene una permeabilidad\(\mu\). El sistema es impulsado por una fuente de corriente continua.
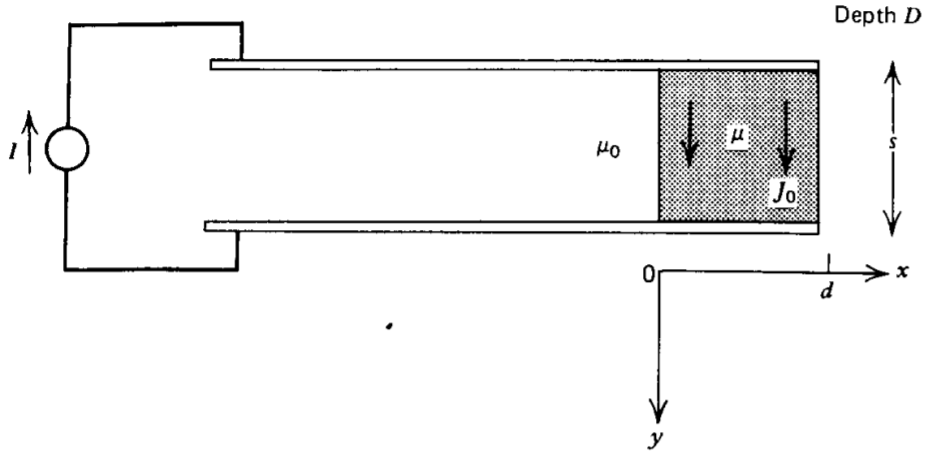
(a) Descuidar los efectos del campo de franjas asumiendo que el campo magnético es\(H_{z}(x) \textbf{i}_{z}\). Si la corriente se distribuye uniformemente por toda la losa, encuentra el campo magnético en todas partes.
b) ¿Cuál es la fuerza total sobre la losa? ¿La fuerza cambia con diferente permeabilidad de losa? ¿Por qué no?
Una losa permeable se inserta parcialmente en el entrehierro de un circuito magnético con campo uniforme\(H_{0}\). Hay un campo de flecos no uniforme justo fuera del circuito magnético cerca de los bordes.
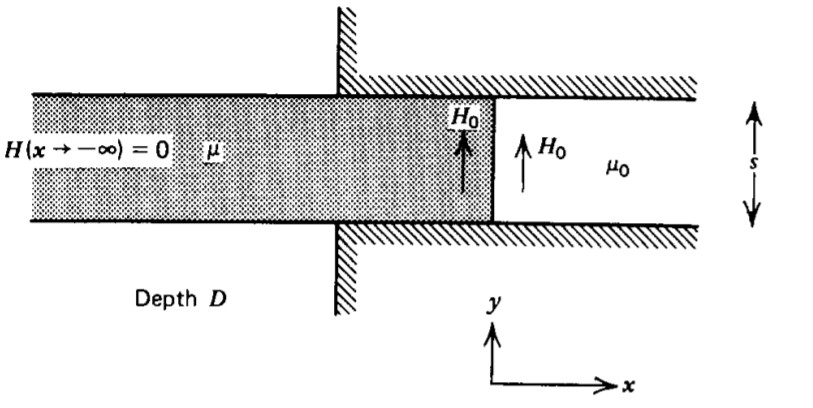
a) ¿Cuál es la fuerza total sobre la losa en la \(x\)dirección?
(b) Repita (a) si la losa está permanentemente magnetizada\(\textbf{M} = M_{0} \textbf{i}_{y}\). (Pista: ¿Qué es\(H_{x}(x = - \infty)\)? Ver Ejemplo 5-2a.)


