3.6: Estado estacionario sinusoidal y el circuito RLC en serie
- Page ID
- 82236
Los fasores pueden ser utilizados para analizar el comportamiento de sistemas eléctricos y mecánicos que han alcanzado una especie de equilibrio llamado estado estacionario sinusoidal. En el estado estacionario sinusoidal, cada voltaje y corriente (o fuerza y velocidad) en un sistema es sinusoidal con frecuencia angular\(ω\). Sin embargo, las amplitudes y fases de estos voltajes y corrientes sinusoidales son todas diferentes. Por ejemplo, el voltaje a través de una resistencia podría conducir el voltaje a través de un condensador en 90° (\(\frac π 2\)radianes) y retardar el voltaje a través de un inductor en 90° (\(\frac π 2\)radianes).
Para hacer concreta nuestra aplicación de fasores a sistemas eléctricos, consideramos el circuito RLC en serie ilustrado en la Figura\(\PageIndex{1}\). La flecha etiquetada\(i(t)\) denota una corriente que fluye en respuesta al voltaje aplicado, y el + y - en la fuente de voltaje indican que la polaridad del voltaje aplicado es positiva en la parte superior y negativa en la parte inferior. Nuestra convención es que la corriente fluye de positiva a negativa, en este caso en sentido horario en el circuito.
Supondremos que la fuente de voltaje es un oscilador de audio que produce el voltaje
\[V(t)=A\cos(ωt+φ) \nonumber \]
Representamos este voltaje como la señal compleja
\[V(t)↔Ae^{jφ}e^{jωt} \nonumber \]
y darle la representación fasora
\[V(t)↔V;V=Ae^{jφ} \nonumber \]
Luego describimos la fuente de voltaje por el fasor V y recordamos que siempre podemos calcular el voltaje real multiplicando por\(e^{jωt}\) y tomando la parte real:
\[V(t)=\mathrm{Re}\{Ve^{jωt}\} \nonumber \]
Demostrar que
\[\mathrm{Re}[Ve^{jωt}]=A\cos(ωt+φ) \nonumber \]
cuando\(V=Ae^{jφ}\).
Leyes de Circuito
En tus clases de circuitos estudiarás las leyes de Kirchhoff que rigen el comportamiento de baja frecuencia de los circuitos construidos a partir de resistencias (R), inductores (L) y condensadores (C). En su estudio aprenderá que el voltaje caído a través de una resistencia está relacionado con la corriente que fluye a través de ella por la ecuación
\[V_R(t)=Ri(t) \nonumber \]
Aprenderá que el voltaje caído a través de un inductor es proporcional a la derivada de la corriente que fluye a través de él, y el voltaje caído a través de un condensador es proporcional a la integral de la corriente que fluye a través de él:
\[V_L(t)=L\frac {di} {dt} (t) \nonumber \]
\[V_C(t)=\frac 1 C ∫i(t)dt \nonumber \]
Fasores e impedancia compleja
Ahora supongamos que la corriente en las ecuaciones precedentes es sinusoidal, de la forma
\[i(t)=B\cos(ωt+θ) \nonumber \]
Podemos reescribir\(i(t)\) como
\[i(t)=\mathrm{Re}\{Ie^{jωt}\} \nonumber \]
donde\(I\) está la representación fasora de\(i(t)\).
Encuentra el fasor\(I\) en términos de\(B\) y\(θ\) en la ecuación anterior.
El voltaje caído a través de la resistencia es
\[\begin{align} V_R(t) &=Ri(t) \\[4pt] &=R\mathrm{Re}\{Ie^{jωt}\} \\[4pt] &=\mathrm{Re}\{RIe^{jωt}\} \end{align} \nonumber \]
Por lo tanto, la representación fasora para\(V_R(t)\) es
\[V_R(t)↔V_R;V_R=RI \nonumber \]
Llamamos a R la impedancia de la resistencia porque R es la constante de escala que relaciona el “voltaje fasor V R 'con la “corriente fasora I”.
El voltaje caído a través del inductor es
\[V_L(t)=L\frac {di}{dt}(t)=L\frac d {dt}\mathrm{Re}\{Ie^{jωt}\} \nonumber \]
La derivada se puede mover a través del operador Re [] (ver Ejercicio) para producir el resultado
\[\begin{align} V_L(t)&=L\mathrm{Re}\{jωIe^{jωt}\} \\[4pt] &=\mathrm{Re}\{jωLIe^{jωt}\} \end{align} \nonumber \]
Así, la representación fástica de\(V_L(t)\)
\[V_L(t)↔V_L;V_L=jωLI \nonumber \]
Llamamos a\(jωL\) la impedancia del inductor porque\(jωL\) es la constante de escala compleja que relaciona “voltaje de fasor\(V_L\)” con “corriente de fasor\(I\).
Demostrar que los operadores\(\frac d {dt}\) y Re [] conmutan:
\(\frac d {dt}\mathrm{Re}\{e^{jωt}\}=\mathrm{Re}\{\frac d {dt} e^{jωt}\}\)
El voltaje caído a través del condensador es
\[V_C(t)=\frac 1 C ∫i(t)dt = \frac 1 C ∫ \mathrm{Re}\{Ie^{jωt}\}dt \nonumber \]
La integral puede moverse a través del operador Re [] para producir el resultado
\[ \begin{align} V_C(t) &=\frac 1 C \mathrm{Re}\{\frac I {jω} e^{jωt}\} \\[4pt] &=\mathrm{Re}\{\frac I {jωC} e^{jωt}\} \end{align} \nonumber \]
Así, la representación fasora de V C (t) es
\[V_C(t)↔V_C;V_C=\frac I {jωC} \nonumber \]
Llamamos a\(\frac 1 {jωC}\) la impedancia del condensador porque\(\frac 1 {jωC}\) es la constante de escala compleja que relaciona “voltaje fasor V C" con “corriente fasor I.”
Ley de Voltaje de Kirchhoff
La ley de voltaje de Kirchhoff dice que el voltaje caído en la combinación en serie de R, L y C ilustrada en la Figura es igual al voltaje generado por la fuente (esta es una de las dos leyes de conservación fundamentales en la teoría de circuitos, siendo la otra una ley de conservación para la corriente):
\[V(t)=V_R(t)+V_L(t)+V_C(t) \nonumber \]
Si reemplazamos todos estos voltajes por sus complejas representaciones, tenemos
\[\mathrm{Re}\{Ve^{jωt}\}=\mathrm{Re}\{(V_R+V_L+V_C)e^{jωt}\} \nonumber \]
Una solución obvia es
\[V=VR+VL+VC \nonumber \]
\[=(R+jωL+\frac 1 {jωC})I \nonumber \]
donde I es la representación fasora para la corriente que fluye en el circuito. Esta solución se ilustra en la Figura, donde los voltajes de fasores\(RI\),\(jωLI\), y\(\frac 1 {jωC} I\) son forzados a sumarse a la tensión de fasor\(V\).
Redibuja la figura anterior para\(R=ωL=\frac 1 {ωC} = 1\)
Impedancia
Llamamos al número complejo\(R+jωL+\frac 1 {jωC}\) la impedancia compleja para la red RLC en serie porque es el número complejo el que relaciona el voltaje fasor V con la corriente fasor I:
\[V=ZI \nonumber \]
\[Z=R+jωL+\frac 1 {jωC} \nonumber \]
El número complejo\(Z\) depende de los valores numéricos de resistencia\((R)\), inductancia\((L)\) y capacitancia\((C)\), pero también depende de la frecuencia angular\((ω)\) utilizada para la fuente sinusoidal. Esta impedancia puede manipularse de la siguiente manera para ponerla en una forma iluminadora:
\[Z=R+j(ωL−\frac 1 {ωC}) \nonumber \]
\[= R+j \sqrt{\frac L C}(ω \sqrt{LC}−\frac 1 {/sqrt{ωLC}}) \nonumber \]
El parámetro\(ω_0=\frac 1 {\sqrt{LC}}\) es un parámetro que aprenderás a llamar una “frecuencia natural no amortiguada” en tus cursos de circuitos más avanzados. Con él, podemos escribir la impedancia como
\[Z=R+jω_0L(\frac ω {ω_0}−\frac {ω_0} ω) \nonumber \]
La frecuencia\(\frac ω {ω_0}\) es una frecuencia normalizada que denotamos por\(ν\). Entonces la impedancia, en función de la frecuencia normalizada, es
\[Z(ν)=R+jω_0L(ν−\frac 1 ν) \nonumber \]
Cuando la frecuencia normalizada es igual a uno\((ν=1)\), entonces la impedancia es completamente real y\(Z=R\). El circuito parece que es una sola resistencia.
\[∣Z(ν)∣∣=R[1+(/frac {ω_0L} R)^2(ν−\frac 1 ν)^2]^{1/2} \nonumber \]
\[\mathrm{arg}Z(ν)=\tan^{−1}\frac {ω_0L} R (ν−\frac 1 ν) \nonumber \]
La impedancia obedece a las siguientes simetrías en torno a\(ν=1\):
\[Z(ν)=Z^∗(\frac 1 ν) \nonumber \]
\[∣Z(ν)∣=∣Z(\frac 1 ν)∣ \nonumber \]
\[\mathrm{arg}Z(ν)=−\mathrm{arg}Z(\frac 1 ν) \nonumber \]
En el siguiente párrafo mostramos cómo esta función de impedancia influye en la corriente que fluye en el circuito.
Resonancia
La representación de fasores para la corriente que fluye la corriente que fluye en el circuito RLC en serie es
\[\begin{align} I &=VZ(ν) \\[4pt] &=1|Z(ν)|e−jargZ(ν)V \end{align} \nonumber \]
La función\(H(ν)=\frac 1 {Z(ν)}\) muestra un “fenómeno de resonancia”. es decir,\(|H(ν)|\) alcanza su punto máximo\(ν=1\) y disminuye a cero y ν=0 y ν=∞:
\[|H(ν)|= \begin{cases} 0, ν=0 \\ \frac 1 R, ν=1 \\ 0, ν=∞ \end{cases} \nonumber \]
Cuando\(|H(ν)|=0\), no fluye corriente.
La función\(|H(ν)|\) se representa frente a la frecuencia normalizada\(ν=\frac ω {ω_0}\) en la Figura. El pico de resonancia ocurre en ν=1, donde\(|H(ν)|=\frac 1 R\) significa que el circuito parece puramente resistivo. Los fenómenos de resonancia subyacen a la selectividad de frecuencia de todas las redes eléctricas y mecánicas.
(MATLAB) Escribir un programa MATLAB para computar y trazar\(|H(ν)|\) y\(argH(ν)\) versus ν para ν que van de 0.1 a 10 en pasos de 0.1. Realiza tus cálculos para\(ω_0LR=10,1,0.1\), y 0.01, y sobregrafica tus resultados.
Criterio de círculo y factor de potencia
Nuestro estudio de la impedancia\(Z(ν)\) y la función\(H(ν)=\frac 1 {Z(ν)}\) aporta información sobre la resonancia de un circuito RLC e ilustra la selectividad de frecuencia del circuito. Pero hay más que podemos hacer para iluminar el comportamiento del circuito.
\[V=RI+j(ωL−\frac 1 {ωC})I \nonumber \]
Esta ecuación muestra cómo se divide el voltaje entre el voltaje del resistor RI y el voltaje del inductor-condensador\(j(ωL−1ωC)I\).
\[V=RI+jω_0L(\frac ω {ω_0}−\frac {ω_0} ω)I \nonumber \]
o
\[V=RI+\frac {jω_0L} R (ν−/frac 1 ν)RI \nonumber \]
Para simplificar nuestra notación, podemos escribir esta ecuación como
\[V=V_R+jk(ν)V_R \nonumber \]
donde\(V_R\) esta el voltaje del fasor\(RI\) y\(k(ν)\) es la variable real
\[k(ν)=\frac {ω_0L} R (ν−\frac 1 ν) \nonumber \]
La ecuación aporta percepciones geométricas muy importantes. Primero, aunque el voltaje fasor\(V_R\) en el circuito RLC es complejo, los términos\(V_R\) y\(jk(ν)V_R\) están desfasados por\(\frac π 2\) radianes. Esto significa que, por cada valor permisible de\(V_R\), el correspondiente\(jk(ν)V_R\) debe sumarse en un triángulo rectángulo para producir la tensión de fuente V. Esto se ilustra en la Figura. A medida que cambia la frecuencia ν, luego\(k(ν)\) cambia, produciendo otros valores de\(V_R\) y\(jk(ν)V_R\) que suman a V. Varias soluciones de este tipo para\(V_R\) y\(jk(ν)V_R\) se ilustran en la Figura 3.15 (b). De la figura obtenemos la clara impresión de que el voltaje del fasor\(V_{>R}\) se encuentra en un círculo de radio\(\frac V 2\) centrado en\(\frac V 2\) Probemos esta solución,
\[V_R=\frac V 2 +\frac V 2 e^{jψ}=\frac V 2 (1+e^{jψ}) \nonumber \]
y explorar sus consecuencias. Cuando esta solución se sustituye en Ecuación, el resultado es
\[V=\frac V 2 (1+e^{jψ})+jk(ν)V_2(1+e^{jψ}) \nonumber \]
o
\[2=(1+e^{jψ})[1+jk(ν)] \nonumber \]
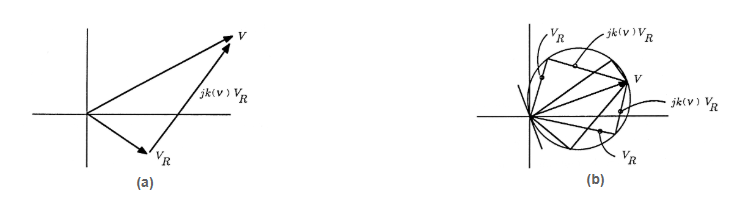
Si multiplicamos el lado izquierdo por su conjugado complejo y el lado derecho por su conjugado complejo, obtenemos la identidad
\[4=2(1+\cosψ)[1+k^2(ν)] \nonumber \]
Esta ecuación nos dice cómo depende el ángulo ψ\(k(ν)\) y, a la inversa, cómo\(k(ν)\) depende de ψ:
\[\cosψ = \frac {1−k^2(ν)} {1+k^2(ν)} \nonumber \]
\[k^2(ν)=\frac {1−\cosψ} {1+\cosψ} \nonumber \]
El número\(\cosψ\) se encuentra entre −1 y +1, por lo que una solución circular sí funciona.
Consultar\(−1≤\cosψ≤1\) por\(−∞<k<∞\) y\(−∞<k<∞\) para\(−π≤ψ≤π\). Sketch\(k\) versus\(ψ\) y\(ψ\) versus\(k\).
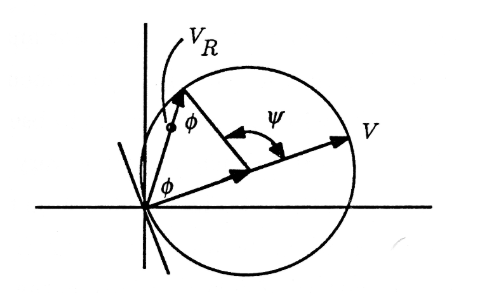
La ecuación\(V_R=\frac V 2 (1+e{jψ})\) se ilustra en la Figura. El ángulo que\(V_R\) hace con\(V\) se determina a partir de la ecuación
\[2φ+π−ψ=π⇒φ=\frac ψ 2 \nonumber \]
En el estudio de los sistemas de potencia, cosφ es un “factor de potencia” que determina cuánta potencia se entrega a la resistencia. Podemos denotar el factor de potencia como
\[η=\cosφ=\cos\frac ψ 2 \nonumber \]
Pero\(\cosψ\) puede escribirse como
\[η=cosφ=cos\frac ψ 2 \nonumber \]
Pero\(\cosψ\) puede escribirse como
\[\begin{align} \cosψ=\cos(φ+φ) &= \cos^2φ−−\sin^2φ \\ &=\cos^2φ−(1−\cos^2φ) \\ &=2\cos^2φ−1 \\ &=2η^2−1 \end{align} \nonumber \]
Por lo tanto, el cuadrado del factor de potencia η es
\[ \eta ^2 = \frac{\cos \psi + 1}{2} = \frac{1}{1+k^2(\nu)} \nonumber \]
El factor de potencia es un máximo de 1 para\(k(ν)=0\), correspondiente a\(ν=1(ω=ω_0)\). Es un mínimo de 0 para\(k(ν)=±∞\), correspondiente a\(ν=0,∞(ω=0,∞)\).
Con\(k\) definido como\(k(ν)=\frac {ω_0L} R (ν−\frac 1 ν)\), parcela\(k^2(ν)\)\(\cosψ\), y\(η^2\) versus\(ν\).
Encuentra el valor de\(ν\) que hace que el factor de potencia\(η=0.707\).