11.3E: Ejercicios
- Page ID
- 112775
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La práctica hace la perfección
En los siguientes ejercicios, grafica cada ecuación usando propiedades.
- \(y=-x^{2}+4 x-3\)
- \(y=-x^{2}+8 x-15\)
- \(y=6 x^{2}+2 x-1\)
- \(y=8 x^{2}-10 x+3\)
- Contestar
-
1.
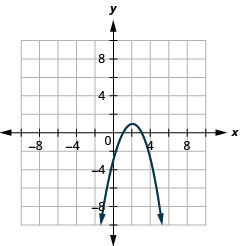
Figura 11.2.83 3.
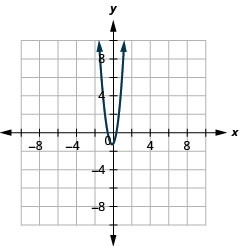
Figura 11.2.84
En los siguientes ejercicios,
- Escribe la ecuación en forma estándar y
- Utilice las propiedades de la forma estándar para graficar la ecuación.
- \(y=-x^{2}+2 x-4\)
- \(y=2 x^{2}+4 x+6\)
- \(y=-2 x^{2}-4 x-5\)
- \(y=3 x^{2}-12 x+7\)
- Contestar
-
1.
- \(y=-(x-1)^{2}-3\)
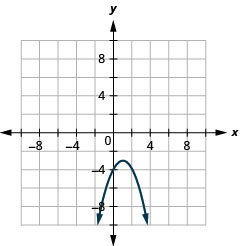
Figura 11.2.85 3.
- \(y=-2(x+1)^{2}-3\)
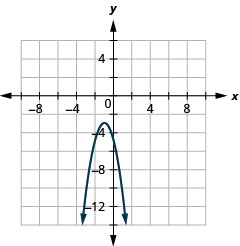
Figura 11.2.86
En los siguientes ejercicios, grafica cada ecuación usando propiedades.
- \(x=-2 y^{2}\)
- \(x=3 y^{2}\)
- \(x=4 y^{2}\)
- \(x=-4 y^{2}\)
- \(x=-y^{2}-2 y+3\)
- \(x=-y^{2}-4 y+5\)
- \(x=y^{2}+6 y+8\)
- \(x=y^{2}-4 y-12\)
- \(x=(y-2)^{2}+3\)
- \(x=(y-1)^{2}+4\)
- \(x=-(y-1)^{2}+2\)
- \(x=-(y-4)^{2}+3\)
- \(x=(y+2)^{2}+1\)
- \(x=(y+1)^{2}+2\)
- \(x=-(y+3)^{2}+2\)
- \(x=-(y+4)^{2}+3\)
- \(x=-3(y-2)^{2}+3\)
- \(x=-2(y-1)^{2}+2\)
- \(x=4(y+1)^{2}-4\)
- \(x=2(y+4)^{2}-2\)
- Contestar
-
1.
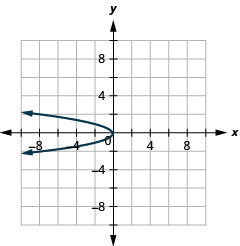
Figura 11.2.87 3.
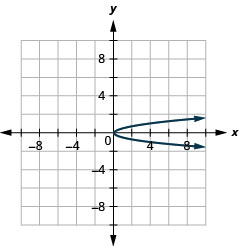
Figura 11.2.88 5.
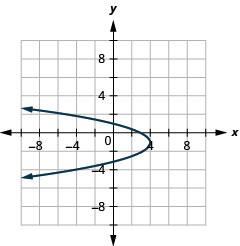
Figura 11.2.89 7.
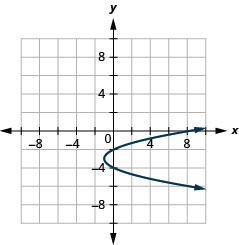
Figura 11.2.90 9.
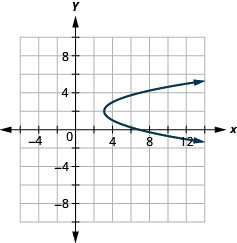
Figura 11.2.91 11.
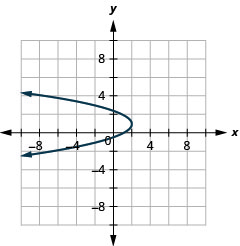
Figura 11.2.92 13.
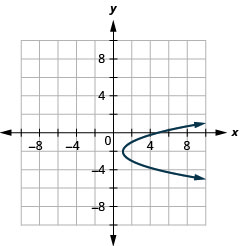
Figura 11.2.93 15.
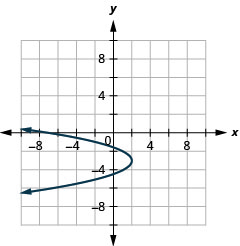
Figura 11.2.94 17.
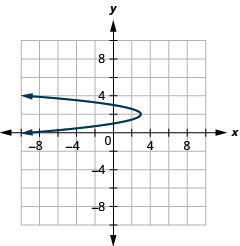
Figura 11.2.95 19.
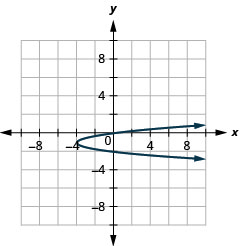
Figura 11.2.96
En los siguientes ejercicios,
- Escribe la ecuación en forma estándar y
- Utilice las propiedades de la forma estándar para graficar la ecuación.
- \(x=y^{2}+4 y-5\)
- \(x=y^{2}+2 y-3\)
- \(x=-2 y^{2}-12 y-16\)
- \(x=-3 y^{2}-6 y-5\)
- Contestar
-
1.
- \(x=(y+2)^{2}-9\)
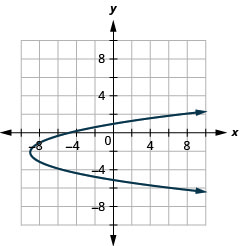
Figura 11.2.97 3.
- \(x=-2(y+3)^{2}+2\)
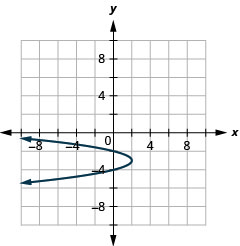
Figura 11.2.98
En los siguientes ejercicios, haga coincidir cada gráfica con una de las siguientes ecuaciones:
- \(x^{2}+y^{2}=64\)
- \(x^{2}+y^{2}=49\)
- \((x+5)^{2}+(y+2)^{2}=4\)
- \((x-2)^{2}+(y-3)^{2}=9\)
- \(y=-x^{2}+8 x-15\)
- \(y=6 x^{2}+2 x-1\)
1.
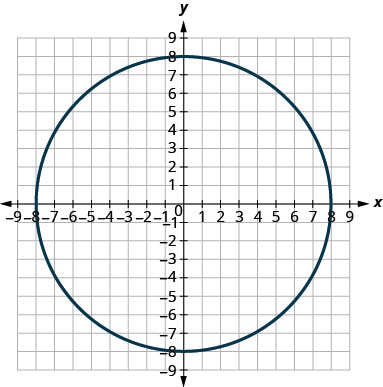
2.
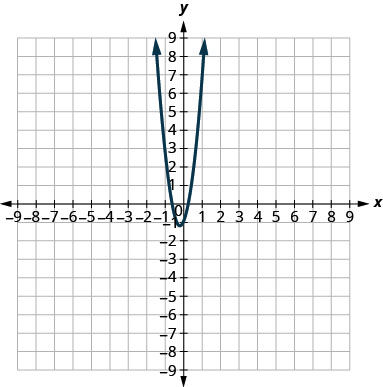
3.
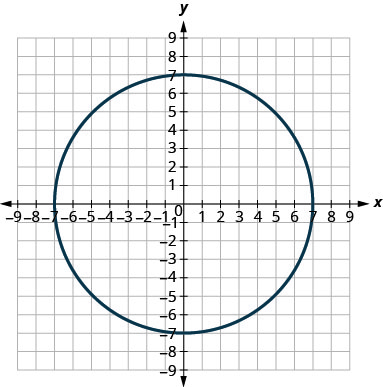
4.
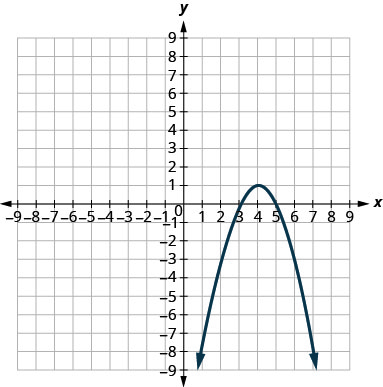
5.
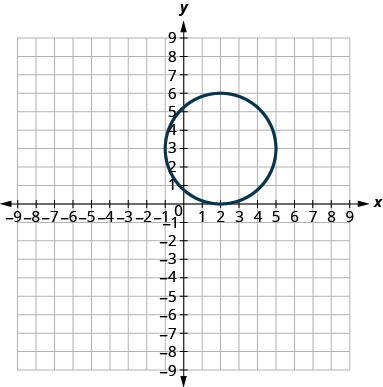
6.
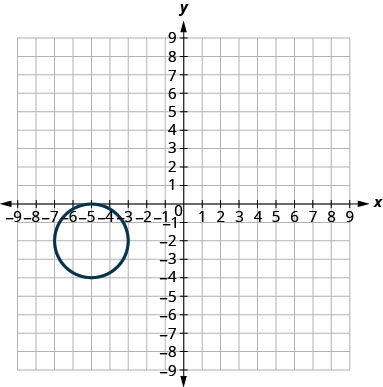
- Contestar
-
1. a
3. b
5. d
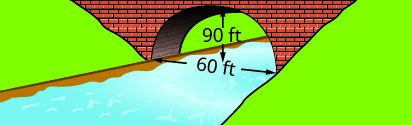
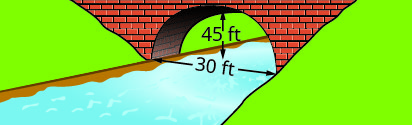
Escribe la ecuación en forma estándar del arco parabólico formado en la cimentación del puente mostrado. Usa el lado inferior izquierdo del puente como origen\((0, 0)\).
1.
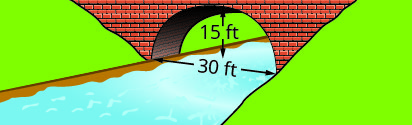
2.
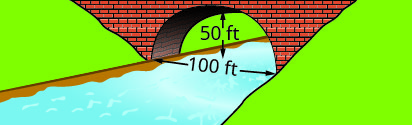
3.
4.
- Contestar
-
1. \(y=-\frac{1}{15}(x-15)^{2}+15\)
3. \(y=-\frac{1}{10}(x-30)^{2}+90\)
- En sus propias palabras, defina una parábola.
- ¿La parábola es\(y=x^{2}\) una función? ¿La parábola es\(x=y^{2}\) una función? Explique por qué o por qué no.
- Escribe la ecuación de una parábola que se abre hacia arriba o hacia abajo en forma estándar y la ecuación de una parábola que se abre a la izquierda o a la derecha en forma estándar. Proporcionar un boceto de la parábola para cada una, etiquetar el vértice y el eje de simetría.
- Explica con tus propias palabras, cómo puedes decir a partir de su ecuación si una parábola se abre hacia arriba, hacia abajo, a la izquierda o a la derecha.
- Contestar
-
1. Las respuestas pueden variar
3. Las respuestas pueden variar
Autocomprobación
a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
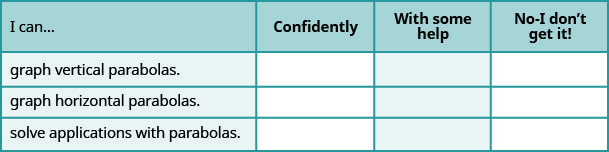
b. Después de revisar esta lista de verificación, ¿qué harás para tener confianza en todos los objetivos?