Prefacio
- Page ID
- 112361
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Prefacio
Álgebra elemental es un texto de trabajo que abarca los temas tradicionales estudiados en un curso de álgebra elemental moderna. Está destinado a estudiantes que:
- Este texto puede ser utilizado en clase estándar o clases a su propio ritmo. Para ayudar a los alumnos a alcanzar estos objetivos y hacer del estudio del álgebra una experiencia placentera y gratificante, el Álgebra Primaria se organiza de la siguiente manera.
Características pedagógicas
- Objetivos
Conjuntos de Muestras
Álgebra elemental contiene ejemplos que se ponen en cajas para facilitar la referencia. Los ejemplos se denominan Conjuntos de Muestras por dos razones:
- Un Conjunto de Práctica paralelo sigue a cada Conjunto de Muestra, lo que refuerza los conceptos recién aprendidos. Las respuestas a todos los Conjuntos de Práctica se muestran con la pregunta al ver este contenido en línea, o al final del capítulo en la versión impresa.
Ejercicios de sección
Los problemas se emparejan para que los problemas impares sean equivalentes en especie y dificultad a los problemas pares. Las respuestas a los problemas impares se proporcionan con el ejercicio cuando se ve en línea, o al final del capítulo en la versión impresa.
Ejercicios para la revisión
Esta sección consiste en problemas que forman una revisión acumulativa del material tratado en los apartados anteriores del texto y no se limita al material de dicho capítulo. Los ejercicios están ordenados por sección para una fácil referencia.
Resumen de Key Concepts
Al final de cada capítulo se incluye un resumen de las ideas y fórmulas importantes utilizadas a lo largo del capítulo. Más que una simple lista de términos, el resumen es una valiosa herramienta que refuerza conceptos en preparación para el Examen de Competencia al final del capítulo, así como exámenes futuros. El resumen arroja cada ítem a la sección del texto donde se discute.
Suplemento de ejercicio
Además de numerosos ejercicios de sección, cada capítulo incluye aproximadamente 100 problemas suplementarios, a los que se hace referencia por sección. Las respuestas a los problemas impares se incluyen con los problemas cuando se ven en línea y en la parte posterior del capítulo en la versión impresa.
Examen de competencia
Cada capítulo termina con un examen de competencia que puede servir como una revisión de capítulo o una evaluación de capítulo. El examen de competencia está clavado en secciones, lo que permite al estudiante referirse al texto para obtener asistencia. Las respuestas a todos los problemas del examen de competencia se incluyen con los ejercicios cuando se ven en línea, o en la parte posterior del capítulo en la versión impresa.
Contenido
El estilo de escritura es informal y amigable, ofreciendo un enfoque sencillo y sensato del álgebra. Hemos hecho un esfuerzo deliberado para no escribir otro texto que minimice el uso de palabras porque creemos que los estudiantes pueden estudiar conceptos algebraicos y entender técnicas algebraicas usando palabras y símbolos en lugar de símbolos solos. Nuestra experiencia ha sido que los estudiantes de nivel elemental no tienen la experiencia suficiente con las matemáticas para entender solo las explicaciones simbólicas; también necesitan leer la explicación.
Hemos tenido mucho cuidado en presentar conceptos y técnicas para que sean comprensibles y fáciles de recordar. Después de que se han desarrollado los conceptos, se advierte a los estudiantes sobre los escollos comunes.
Revisión Aritmética
Este capítulo contiene muchos ejemplos de técnicas aritméticas que se utilizan directa o indirectamente en álgebra. Dado que el capítulo pretende ser una revisión, las técnicas de resolución de problemas se presentan sin ser desarrolladas. Por lo tanto, no se proporciona espacio de trabajo, ni el capítulo contiene todas las características pedagógicas del texto. Como revisión, este capítulo puede ser asignado a discreción del instructor y también puede ser una valiosa herramienta de referencia para el alumno.
Propiedades Básicas de Números Reales
Los símbolos, las notaciones y las propiedades de los números que forman la base del álgebra, así como los exponentes y las reglas de los exponentes, se introducen en Propiedades Básicas de los Números Reales. Cada propiedad de los números reales y las reglas de los exponentes se expresan tanto simbólica como literalmente. Se incluyen explicaciones literales porque las explicaciones simbólicas por sí solas pueden ser difíciles de interpretar para un estudiante.
Operaciones Básicas con Números Reales
En este capítulo se presentan las operaciones básicas con números reales. El concepto de valor absoluto se discute tanto geométrica como simbólicamente. La presentación geométrica ofrece una comprensión visual del significado de x. La presentación simbólica incluye una explicación literal de cómo usar la definición. Se desarrollan exponentes negativos, utilizando reciprocales y las reglas de exponentes que el alumno ya ha aprendido. También se incluye la notación científica, utilizando ejemplos únicos y de la vida real.
Expresiones y ecuaciones algebraicas
Las operaciones con expresiones algebraicas y evaluaciones numéricas se introducen en Expresiones y Ecuaciones Algebraicas. Los coeficientes se describen en lugar de limitarse a definir. Los productos binomiales especiales tienen tanto explicación simbólica literal como como ocurren con tanta frecuencia en matemáticas, hemos tenido cuidado de ayudar al alumno a recordarlos. En cada problema de ejemplo, el alumno es “platicado” a través de la forma simbólica.
Resolver ecuaciones lineales y desigualdades
En este capítulo, el énfasis está en la mecánica de la resolución de ecuaciones, lo que explica claramente cómo aislar una variable. El objetivo es ayudar al alumno a sentirse más cómodo resolviendo problemas aplicados. Se brinda amplia oportunidad para que el estudiante practique la traducción de palabras a símbolos, lo cual es una parte importante del “Método de los Cinco Pasos” para resolver problemas aplicados (discutido en la Sección 5.6 y Sección 5.7).
Factorización de polinomios
El factoring es una habilidad esencial para el éxito en los cursos de álgebra y matemáticas de nivel superior. Por lo tanto, hemos tenido mucho cuidado en desarrollar la comprensión del estudiante sobre el proceso de factorización. La técnica se ilustra consistentemente mostrando un conjunto vacío de paréntesis y describiendo el proceso de pensamiento utilizado para descubrir los términos que se van a colocar dentro de los paréntesis.
El esquema de factorización para productos especiales se presenta con descripciones tanto verbales como simbólicas, ya que no todos los estudiantes pueden interpretar descripciones simbólicas por sí solos. Se presentan dos técnicas, el método estándar de “ensayo y error” y el método de “recolectar y descartar” (un método similar al método “ac”), para factorizar trinomios con coeficientes principales diferentes de 1.
Graficar ecuaciones lineales y desigualdades en una y dos variables
En este capítulo se muestra al alumno cómo las gráficas proporcionan información que no siempre es evidente a partir de la ecuación por sí sola. El capítulo comienza estableciendo la relación entre las variables en una ecuación, el número de ejes de coordenadas necesarios para construir la gráfica, y la dimensión espacial tanto del sistema de coordenadas como de la gráfica. También se enfatiza la interpretación de las gráficas a lo largo del capítulo, comenzando con el trazado de puntos. La fórmula de pendiente está completamente desarrollada, progresando de frases verbales a expresiones matemáticas. Luego, las expresiones se forman en una ecuación al afirmar explícitamente que una relación es una comparación de dos cantidades del mismo tipo (por ejemplo, distancia, peso o dinero). Este enfoque beneficia a los estudiantes que toman cursos futuros que utilizan gráficos para mostrar información.
Al alumno se le muestra cómo graficar líneas utilizando el método de intercepción, el método de tabla y el método pendiente-intercepción, así como cómo distinguir, por inspección, líneas oblicuas y horizontales/verticales.
Expresiones racionales
En este capítulo se presenta un estudio detallado de las operaciones aritméticas con expresiones racionales, comenzando con la definición de una expresión racional y luego procediendo inmediatamente a una discusión del dominio. También se incluye el proceso de reducción de una expresión racional e ilustraciones de multiplicar, dividir, sumar y restar expresiones racionales. Dado que las operaciones de suma y resta pueden ocasionar la mayor dificultad, se les presta especial atención. Hemos tratado de hacer más clara la explicación escrita de los ejemplos mediante el uso de un enfoque de “congelación de fotogramas.
El método de cinco pasos para resolver problemas aplicados se incluye en este capítulo para mostrar el enfoque de resolución de problemas de números, problemas de trabajo y problemas de geometría. El capítulo también ilustra la simplificación de expresiones racionales complejas, utilizando el método combine-divide y el método LCD-Multiply-Divide.
Ecuaciones de Raíces, Radicales y Raíz Cuadrada
Se hace la distinción entre la raíz cuadrada principal del número x
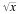 , y la raíz cuadrada secundaria del número
x
, y la raíz cuadrada secundaria del número
x
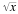 , por explicación y por ejemplo. La simplificación de expresiones radicales que involucran y no involucran fracciones se muestra en muchos ejemplos detallados; esto es seguido por una explicación de cómo y por qué los radicales son eliminados del denominador de una expresión radical. Se han incluido aplicaciones de la vida real de ecuaciones radicales, como problemas relacionados con la producción diaria, las ventas diarias, la frecuencia de resonancia electrónica y la energía cinética.
, por explicación y por ejemplo. La simplificación de expresiones radicales que involucran y no involucran fracciones se muestra en muchos ejemplos detallados; esto es seguido por una explicación de cómo y por qué los radicales son eliminados del denominador de una expresión radical. Se han incluido aplicaciones de la vida real de ecuaciones radicales, como problemas relacionados con la producción diaria, las ventas diarias, la frecuencia de resonancia electrónica y la energía cinética.Ecuaciones cuadráticas
Se discuten los métodos de resolución de ecuaciones cuadráticas así como la lógica subyacente a cada método. La factorización, la extracción de raíces, la finalización del cuadrado y la fórmula cuadrática se desarrollan cuidadosamente. Se reintroduce la propiedad de factor cero de los números reales. El capítulo también incluye gráficas de ecuaciones cuadráticas basadas en la parábola estándar, y = x 2 , y problemas aplicados de las áreas de manufactura, población, física, geometría, matemáticas (número y volúmenes), y astronomía, que se resuelven mediante el método de cinco pasos.
Sistemas de Ecuaciones Lineales
Comenzando con la solución gráfica de los sistemas, este capítulo incluye una interpretación de sistemas independientes, inconsistentes y dependientes y ejemplos para ilustrar las aplicaciones de estos sistemas. Se explica el método de sustitución y el método de adición para resolver un sistema por eliminación, señalando cuándo usar cada método. El método de cinco pasos se utiliza nuevamente para ilustrar las soluciones de problemas de valor y tasa (problemas de monedas y mezclas), utilizando dibujos que corresponden a la solución real.
- Un Conjunto de Práctica paralelo sigue a cada Conjunto de Muestra, lo que refuerza los conceptos recién aprendidos. Las respuestas a todos los Conjuntos de Práctica se muestran con la pregunta al ver este contenido en línea, o al final del capítulo en la versión impresa.
- Objetivos


