5.6: Aplicación II - Solución de Problemas
( \newcommand{\kernel}{\mathrm{null}\,}\)
Solución de Problemas Aplicados
Estudiemos algunos problemas interesantes que involucran ecuaciones lineales en una variable. Para resolver este tipo de problemas, aplicamos el siguiente método de cinco pasos:
Método de cinco pasos para resolver problemas verbales
- Quex (o alguna otra letra) represente la cantidad desconocida.
- Traducir las palabras a símbolos matemáticos y formar una ecuación.
- Resuelve esta ecuación.
- Pregúntate “¿Este resultado parece razonable?” Verifique la solución sustituyendo el resultado en la declaración original del problema.
Si la respuesta no se comprueba, o bien has resuelto la ecuación incorrectamente, o has desarrollado la ecuación equivocada. Verifique primero su método de solución. Si el resultado no comprueba, reconsidera tu ecuación.
- Escribe la conclusión.
Si ha sido tu experiencia que los problemas verbales son difíciles, entonces sigue el método de cinco pasos cuidadosamente. La mayoría de las personas tienen dificultades porque descuidan el paso 1.
Siempre empieza por PRESENTAR UNA VARIABLE!
Tenga en cuenta lo que representa la variable a lo largo del problema.
Conjunto de Muestras A
Este año un artículo cuesta 44 dólares, un incremento de $3 con respecto al precio del año pasado. ¿Cuál fue el precio del año pasado?
\ (\ begin {array} {Flushleft}
\ text {Paso 1:}\ text {Dejar} x&=&\ text {precio del año pasado}\\
\ text {Paso 2:} x+3&=&44&x+3\ text {representa el incremento de\ $3 en el precio.} \\
\ text {Paso 3:} &x+3&=&44\\
&x+3-3&=&44-3\\
&x&=&41\\
\ text {Paso 4:} &41+3&=&44&\ text {Sí, esto es correcto}\\
\ text {Paso 5: El precio del año pasado fue\ $41}.
\ end {array}\)
Conjunto de práctica A
Este año un artículo cuesta 23 dólares, un incremento de 4 dólares con respecto al precio del año pasado. ¿Cuál fue el precio del año pasado?
- Letx=
- El precio del año pasado fue.
- Contestar
-
El precio del año pasado fue de $19
Conjunto de Muestras B
El perímetro (longitud alrededor) de un cuadrado es de 60 cm (centímetros). Encuentra la longitud de un lado.
Paso 1: Vamosx= length of a side..
Paso 2: Podemos dibujar un cuadro.
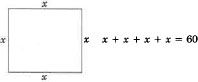
\ (\ begin {array} {Flushleft}
\ text {Paso 3:} &x+x+x+x&=&60\\
&4x&=&60&\ text {Divide ambos lados por 4.} \\
&x&=&15\\
\ text {Paso 4:} &4 (15) &=&60&\ text {Sí, esto es correcto}\\
\ text {Paso 5:} &\ text {La longitud de un lado es de 15 cm}
\ end {array}\)
Set de práctica B
El perímetro de un triángulo es de 54 pulgadas. Si cada lado tiene la misma longitud, encuentra la longitud de un lado.
- Letx=
- La longitud de un lado es de pulgadas.
- Contestar
-
La longitud de un lado es de 18 pulgadas.
Conjunto de Muestras C
El seis por ciento de un número es 54. ¿Cuál es el número?
\ (\ begin {array} {Flushleft}
\ text {Paso 1:} &\ text {Let} x =\ text {el número}\
\\ text {Paso 2:} &\ text {Debemos convertir 6% a un decimal}\\
\ end {array}\)
\ (\ begin {array} {Flushleft}
&6\ %&=&.06\\
&.06x& =&54&.06x\ text {ocurre porque queremos 6% de} x.\\
\ text {Paso 3:} &.06x&=&54&\ text {Divide ambos lados por} .06. \\
&x&=&\ dfrac {54} {.06}\\
&x&=&900\\
\ text {Paso 4:} &.06 (900) &=&54. &\ text {Sí, esto es correcto.} \\
\ text {Paso 5:} &\ text {El número es} 900.
\ end {array}\)
Set de práctica C
El ocho por ciento de un número es 36. ¿Cuál es el número?
- Letx=
- El número es.
- Contestar
-
El número es 450.
Conjunto de Muestras D
Un astrónomo nota que una estrella emite aproximadamente 3.6 veces más energía que otra estrella. Juntas las estrellas desprenden 55.844 unidades de energía. ¿Cuántas unidades de energía emite cada estrella?
1. En este problema tenemos dos incógnitas y, por lo tanto, podríamos pensar, dos variables. No obstante, fíjense que la energía que desprende una estrella se da en términos de la otra estrella. Entonces, en lugar de introducir dos variables, introducimos solo una. El otro (s) desconocido (s) se expresa en términos de éste. (Podríamos llamar a esta cantidad la cantidad base.)
Dejarx= número de unidades de energía desprendidas por la estrella menos energética. Entonces,3.6x= número de unidades de energía emitidas por la estrella más enérgica.
\ (\ begin {array} {Flushleft}
\ text {Paso 2:} &x+3.6x&=&55.844\\
\ text {Paso 3:} &x+3.6x&=&55.844\\
&4.6x&=&55.844&\ text {Divide ambos lados por} 4.6\ text {. Una calculadora sería útil en este punto.} \\
&x&=&\ dfrac {55.844} {4.6}\\
&x&=&12.14&\ text {La redacción del problema implica que se necesitan dos números}\\
&&&&&\ text {para una solución completa. Necesitamos el número de unidades de}\\
&&&&&\ text {energía para la otra estrella.} \\
&3.6x&=&3.6 (12.14)\\
&&=&43.704\\
\ text {Paso 4:} &12.14+43.704&=&55.844&\ text {Sí, esto es correcto}.
\ end {array}\)
Step 5: One start gives off 12.14 units of energy and the other star gives off 43.704 units of energy
Set de Práctica D
El jardín A produce 5.8 veces más verduras que el jardín B. Juntos los huertos producen 102 libras de vegetales. ¿Cuántos kilos de verduras produce el huerto A?
- Letx=
- Contestar
-
El Jardín A produce 87 libras de vegetales.
Juego de Muestras E
Dos números pares consecutivos suman 432. ¿Cuáles son los dos números?
\ (\ text {Paso 1: Dejar} x=\ text {el número par más pequeño. Entonces} x+2=\ text {el siguiente número par (consecutivo)}\\
\ text {ya que los números pares consecutivos difieren en} 2\ text {(al igual que los números impares consecutivos)}\)
\ (\ begin {array} {Flushleft}
\ text {Paso 2:} &x+x+2&=&432\
\\ texto {Paso 3:} &x+x+2&=&432\\
&2x+2&=&432\\
&2x&=&430\\
&x&=&215&\ text {También, desde} x=215, x+2 = 217
\ fin {matriz}\)
\ (\ text {Paso 4:} 215+217=432,\ text {pero} 215\ text {y} 217\ text {son números impares y estamos buscando números pares.} \\
\ text {Al verificar nuestro método de solución y reexaminar nuestra ecuación, no encontramos}\\
\ text {errores.}\)
Step 5: We must conclude that this problem has no solution. There are no two consecutive even numbers that sum to 432
Set de práctica E
La suma de dos números pares consecutivos es 498. ¿Cuáles son los dos números?
- Contestar
-
Los dos números son 248 y 250.
Ejercicios
Resolver los siguientes problemas. Tenga en cuenta que algunos de los problemas pueden parecer no tener aplicaciones prácticas y pueden no parecer muy interesantes. Ellos, junto con los demás problemas, ayudarán, sin embargo, a desarrollar tu lógica y capacidad de resolución de problemas.
Si se resta dieciocho de algún número el resultado es cincuenta y dos. ¿Cuál es el número?
- Letx=
- La ecuación es
- (Resuelve la ecuación.)
- (Comprobar)
- El número es.
- Contestar
-
Paso 1: Dejar quex= la cantidad desconocida.
Paso 2: La ecuación esx−18=52.
Paso 3: (Resuelve la ecuación.) Agrega 18 a cada lado.
\ (x−18+18=52+18\\
x=70\)
Paso 4: (Comprobar)70−18=52; Verdadero.
Paso 5: El número es 70.
Si nueve más de dos veces por número es cuarenta y seis, ¿cuál es el número?
- Letx=
- La ecuación es
- (Resuelve la ecuación.)
- (Comprobar)
- El número es.
Si nueve menos de tres octavos de un número es dos y un cuarto, ¿cuál es el número?
- Letx=
- El número es.
- Contestar
-
Paso 5: El número es 30.
El veinte por ciento de un número es 68. ¿Cuál es el número?
- Letx=
- El número es.
Ocho más que una cantidad es 37. ¿Cuál es la cantidad original?
- Letx=
- La cantidad original es.
- Contestar
-
Paso 5: La cantidad original es 29.
Si una cantidad más 85% más de la cantidad es 62.9, ¿cuál es la cantidad original?
- Dejar x= cantidad original.
- La cantidad original es.
Una empresa debe incrementar la producción en 12% con respecto a la producción del año pasado. La nueva salida será de 56 ítems. ¿Cuál fue la producción del año pasado?
- LetP=
- La producción del año pasado fue de ítems.
- Contestar
-
Paso 5: La producción del año pasado fue de 50 ítems.
Una empresa ha determinado que debe incrementar la producción de cierta línea de bienes por112 tiempos de producción del año pasado. La nueva salida será de 2885 ítems. ¿Cuál fue la producción del año pasado?
- La producción del año pasado fue de ítems.
Un protón es aproximadamente 1837 veces más pesado que un electrón. Si un electrón pesa 2.68 unidades, ¿cuántas unidades pesa un protón?
- Un protón pesa unidades.
- Contestar
-
Paso 5: Un protón pesa 4923.16 unidades.
Tres enteros consecutivos suman 36. ¿Qué son?
- Contestar
-
Paso 5: El primer número entero es 11; el segundo es 12; el tercero es 13.
Neptuno está aproximadamente 30 veces más lejos del sol que la Tierra. Si la luz tarda 8 minutos en viajar del sol a la Tierra, ¿cuántos minutos se tarda en viajar a Neptuno?
- La luz tarda minutos en llegar a Neptuno.
El radio del sol es de unos 695,202 km (kilómetros). Eso es aproximadamente 109 veces más grande que el radio de la Tierra. ¿Cuál es el radio de la tierra?
- El radio de la tierra es km.
- Contestar
-
Paso 5: El radio de la tierra es de 6378 km.
Tres enteros pares consecutivos suman 131. ¿Qué son?
El perímetro de un triángulo es de 105 cm. Si cada una de las dos patas es exactamente el doble de la longitud de la base, ¿cuánto dura cada pata?
- Deja=
Dibujar un cuadro. - Cada pierna mide cm de largo. La base es.
Una empresa maderera ha contratado cortar tablas en dos piezas para que una pieza sea tres veces la longitud de la otra. Si una tabla mide 12 pies de largo, ¿cuál es la longitud de cada pieza después del corte?
- La longitud de la pieza más corta es pies, y la longitud de la pieza más larga es pies.
- Contestar
-
Paso 5: La longitud de la pieza más corta es de 3 pies y la longitud de la pieza más larga es de 9 pies.
Dos enteros impares consecutivos suman 151. ¿Qué son?
Un estudiante que realiza un experimento de química tiene un vaso de precipitados que contiene 84 ml (mililitros) de una solución de alcohol y agua. Sus instrucciones de laboratorio le dicen que hay 4.6 veces más agua que alcohol en la solución. ¿Cuántos mililitros de alcohol hay en la solución? ¿Cuántos mililitros de agua?
- Hay ml de alcohol en la solución. Hay ml de agua en la solución.
Un estadístico está recopilando datos para ayudarle a estimar el ingreso promedio de los contadores en California. Necesita recolectar 390 datos y ya23 está. ¿Cuántos datos ha recopilado el estadístico?
- El estadístico ha recabado datos.
Supongamos que el estadístico está a 4 piezas de datos por debajo de23 hacerse. ¿Cuántos datos ha recopilado?
- Contestar
-
Paso 5: El estadístico ha recabado 260 datos.
Un comercial de televisión anuncia que cierto tipo de batería durará, en promedio, 20 horas más que el doble de la vida de otro tipo de batería. Si las pruebas de consumo muestran que la batería anunciada dura 725 horas, ¿cuántas horas debe durar el otro tipo de batería para que la afirmación del anunciante sea válida?
- El otro tipo de batería debe durar horas para que el reclamo del anunciante sea válido.
Un matraz de 1000 ml que contiene una solución de cloruro llenará 3 vasos del mismo tamaño con 210 ml de la solución sobrante. ¿Cuántos mililitros de la solución de cloruro contendrá cada vaso de precipitados?
- Cada vaso de precipitados contendrá ml de la solución de cloruro.
- Contestar
-
Paso 5: Cada vaso de precipitados contendrá26313 ml de solución de cloruro.
Una estrella quema29 de su masa original y luego sopla37 de la masa restante como una nebulosa planetaria. Si la masa final es de 3 unidades de masa, ¿cuál fue la masa original?
- La masa original era unidades de masa.
La suma de un número y dieciséis es cuarenta y dos. ¿Cuál es el número?
- Contestar
-
Paso 5: El número desconocido es 26.
Cuando se resta once de un número, el resultado es 85. ¿Cuál es el número?
Tres veces un número se divide por 6 y el resultado es 10.5. ¿Cuál es el número?
- Contestar
-
Paso 5: El número desconocido es 21.
Cuando un número se multiplica por sí mismo, el resultado es 144. ¿Cuál es el número?
Un número se triplica, luego se incrementa en siete. El resultado es 48. ¿Cuál es el número?
- Contestar
-
Paso 5: El número desconocido es413.
Ocho veces un número se disminuye tres veces el número, dando una diferencia de 22. ¿Cuál es el número?
Un número es quince más que otro número. La suma de los dos números es 27. ¿Qué son?
- Contestar
-
Paso 5: Un número desconocido es 6; el otro es 21.
La longitud de un rectángulo es de 6 metros más de tres veces el ancho. El perímetro del rectángulo es de 44 metros ¿Cuáles son las dimensiones del rectángulo?
Se agrega siete al producto de 41 y algún número. El resultado, cuando se divide por cuatro, es de 63. ¿Cuál es el número?
- Contestar
-
Paso 5: El número desconocido es24541.
El segundo lado de un triángulo es cinco veces la longitud del lado más pequeño. El tercero es el doble de la longitud del segundo lado. El perímetro del triángulo es de 48 pulgadas. Encuentra la longitud de cada lado.
La persona A tiene cuatro veces más edad que la persona B, que es seis veces mayor que la persona C, que tiene el doble de edad que la persona D. ¿Qué edad tiene cada persona si sus edades combinadas son 189 meses?
Como consecuencia de la teoría de la relatividad de Einstein, la tasa de paso del tiempo es diferente para una persona en una posición estacionaria y una persona en movimiento. (¡Difícil de creer, pero cierto!) Para el observador en movimiento, la velocidad de paso del tiempo es más lenta que la del observador estacionario, es decir, la persona en movimiento envejece más lentamente que el observador estacionario. (Este hecho ha sido probado muchas veces por experimentos con materiales radiactivos). El efecto se llama “dilatación del tiempo” y en realidad solo se nota cuando un objeto viaja cerca de la velocidad de la luz (186,000 millas por segundo). Teniendo en cuenta estas ideas, trata de resolver los siguientes problemas:
Dos personas tienen relojes idénticos. Uno está parado en la tierra y el otro se mueve en una nave espacial a 95% la velocidad de la luz, 176,700 millas por segundo. La tasa de paso del tiempo de la persona en movimiento a esta velocidad es aproximadamente 0.31 veces más rápida que la persona que está de pie en la tierra.
- Si pasan dos días de tiempo terrestre, ¿cuántos días pasan realmente en la nave espacial?
- Si pasan 30 años de tiempo terrestre, ¿cuántos años han pasado realmente en la nave espacial?
- años han pasado en la nave espacial.
- Si han pasado 30 años en la nave espacial, ¿cuántos años han pasado en la tierra?
- Un viajero espacial realiza un viaje de ida y vuelta a la estrella Capella. El viaje le lleva 120 años (viajando a 176,000 millas por segundo). Si es el año 2000 en la tierra cuando se va, ¿qué año terrestre será cuando regrese?
- Contestar
-
a) Paso 5: El tiempo transcurrido en el espacio es de 0.62 días.
b) Paso 5: Han pasado 9.3 años en la nave espacial.
(c) Paso 5: Han pasado 96.77 años en la tierra.
(d) Paso 5: El año de la Tierra cuando regrese será de 2387.
Ejercicios para la revisión
Especificar el dominio de la ecuacióny=x−1x+4
Clasificar la ecuaciónx+4=1 como una identidad, una contradicción o una ecuación condicional.
- Contestar
-
condicional
Clasificar la ecuación2x+3=2x+3 como una identidad, una contradicción o una ecuación condicional.
Resuelve la ecuación4(x−1)+12=−3(2x+4).
- Contestar
-
x=−2
Traducir la siguiente oración a una ecuación matemática. Tres menos que un número desconocido se multiplica por cuatro negativos. El resultado es dos más que el número desconocido original.


