5.8: Ecuaciones lineales en dos variables
- Page ID
- 112175
Soluciones a Ecuaciones Lineales en Dos Variables
Solución a una ecuación en dos variables
Hemos descubierto que una ecuación es una forma matemática de expresar la relación de igualdad entre cantidades. Si la relación es entre dos cantidades, la ecuación contendrá dos variables. Decimos que una ecuación en dos variables tiene una solución si se puede encontrar un par ordenado de valores de tal manera que cuando estos dos valores se sustituyen en la ecuación se obtiene una declaración verdadera. Esto se ilustra cuando observamos algunas soluciones a la ecuación\(y=2x+5\).
\ (\ begin {array} {l}
x=4, y=13;\ quad\ text {desde} 13=2 (4) +5\ text {es verdadero}\\
x=1, y=7;\ quad\ text {desde} 7=2 (1) +5\ text {es verdadero.}\\
x=0, y=5;\ quad\ text {desde} 5=2 (0) +5\ texto {es cierto.}\\
x=-6, y=-7;\ quad\ text {desde} -7=2 (-6) +5\ text {es verdadero.}
\ end {array}\)
Pares ordenados como soluciones
Es importante tener en cuenta que una solución a una ecuación lineal en dos variables es un par ordenado de valores, un valor por cada variable. No se conoce completamente una solución hasta que se especifican los valores de ambas variables.
Variables independientes y dependientes
Recordemos que, en una ecuación, se dice que cualquier variable cuyo valor pueda asignarse libremente es una variable independiente. Cualquier variable cuyo valor se determine una vez asignado el otro valor o valores se dice que es una variable dependiente. Si, en una ecuación lineal, la variable independiente es x y la variable dependiente es y, y una solución a la ecuación es x=a e y=b, la solución se escribe como
PAR ORDENADO:\((a, b)\)
Par Pedido
En un par ordenado,\((a, b)\), el primer componente,\(a\), da el valor de la variable independiente, y el segundo componente,\(b\), da el valor de la variable dependiente.
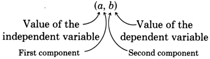
Podemos usar pares ordenados para mostrar algunas soluciones a la ecuación\(y=6x−7\).
\((0, -7)\)
Si\(x = 0\) y\(y = -7\), obtenemos una declaración verdadera tras la sustitución y el cálculo
\ (\ begin {array} {flushleft}
y&=&6x-7\\
-7&=&6 (0) -7&\ text {¿Es esto correcto?} \\
-7&=&-7&\ text {¿Esto es correcto?} \\
-7&=&41&\ text {Sí, esto es correcto}
\ end {array}\)
\((8, 41)\)
Si\(x = 8\) y\(y = 41\), obtenemos una declaración verdadera tras la sustitución y el cálculo
\ (\ begin {array} {flushleft}
y&=&6x-7\\
41&=&6 (8) -7&\ text {¿Es esto correcto?} \\
41&=&48-7&\ text {¿Es esto correcto?} \\
41&=&41&\ text {Sí, esto es correcto}
\ end {array}\)
\((-4, -31)\)
Si\(x = 8\) y\(y = 41\), obtenemos una declaración verdadera tras la sustitución y el cálculo
\ (\ begin {array} {flushleft}
y&=&6x-7\\
-31&=&6 (-4) -7&\ text {¿Es esto correcto?} \\
-31&=&-24-7&\ text {¿Es esto correcto?} \\
-31&=&-31&\ text {Sí, esto es correcto}
\ end {array}\)
Estas son sólo tres de las infinitamente muchas soluciones a esta ecuación.
Conjunto de Muestras A
Encuentre una solución a cada una de las siguientes ecuaciones lineales en dos variables y escriba la solución como un par ordenado.
\ (
y=3 x-6,\ text {if} x=1
\)
Sustituir 1 por\(x\), computar y resolver para\(y\).
\ (
\ begin {aligned}
y &=3 (1) -6\\
&=3-6\\
&=-3
\ end {aligned}
\)
Por lo tanto, una solución es\((1,-3)\).
\ (
y=15-4 x,\ text {if} x=-10
\)
Sustituir -10 por\(x\), computar y resolver para\(y\).
\ (
\ begin {aligned}
y &=15-4 (-10)\\
&=15+40\\
&=55
\ end {aligned}
\)
Por lo tanto, una solución es\((-10,55)\).
\ (
b=-9 a+21,\ text {if} a=2
\)
Sustituir 2 por\(a\), computar y resolver para\(b\).
\ (
\ begin {aligned}
b &=-9 (2) +21\\
&=-18+21\\
&=3
\ end {aligned}
\)
Por lo tanto, una solución es\((2,3)\).
\(5 x-2 y=1, \text{ if } x=0\)
Sustituir 0 por\(x\), computar y resolver para\(y\).
\ (
\ begin {aligned}
5 (0) -2 y &=1\\
0-2 y &=1\\
-2 y &=1\\ y &=\
y &=-\ dfrac {1} {2}
\ end {alineado}
\)
Por lo tanto, una solución es\(\left(0,-\dfrac{1}{2}\right)\).
Conjunto de práctica A
Encuentre una solución a cada una de las siguientes ecuaciones lineales en dos variables y escriba la solución como un par ordenado.
\(y=7x−20\), si\(x=3\)
- Contestar
-
\((3, 1)\)
\(m=−6n+1\), si\(n=2\)
- Contestar
-
\((2, −11)\)
\(b=3a−7\), si\(a=0\)
- Contestar
-
\((0, −7)\)
\(10x−5y−20=0\), si\(x=−8\)
- Contestar
-
\((−8, −20)\)
\(3a+2b+6=0\), si\(a=−1\)
- Contestar
-
\((-1, \dfrac{-3}{2})\)
Ejercicios
Para los siguientes problemas, resolver las ecuaciones lineales en dos variables.
\(y=8x+14\), si\(x=1\)
- Contestar
-
\((1,22)\)
\(y=−2x+1\), si\(x=0\)
\(y=5x+6\), si\(x=4\)
- Contestar
-
\((4,26)\)
\(x+y=7\), si\(x=8\)
\(3x+4y=0\), si\(x=−3\)
- Contestar
-
\((-3, \dfrac{9}{4})\)
\(−2x+y=1\), si\(x=\dfrac{1}{2}\)
\(5x−3y+1=0\), si\(x=−6\)
- Contestar
-
\((-6, -\dfrac{29}{3})\)
\(−4x−4y=4\), si\(y=7\)
\(2x+6y=1\), si\(y=0\)
- Contestar
-
\((\dfrac{1}{2}, 0)\)
\(−x−y=0\), si\(y=\dfrac{14}{3}\)
\(y=x\), si\(x=1\)
- Contestar
-
\((1,1)\)
\(x+y=0\), si\(x=0\)
\(y + \dfrac{3}{4} = x\), si\(x = \dfrac{9}{4}\)
- Contestar
-
\((\dfrac{9}{4}, \dfrac{3}{2})\)
\(y+17=x\), si\(x=−12\)
\(−20y+14x=1\), si\(x=8\)
- Contestar
-
\((8, \dfrac{111}{20})\)
\(\dfrac{3}{5}y + \dfrac{1}{4}x = \dfrac{1}{2}\), si\(x = -3\)
\(\dfrac{1}{5}x + y = -9\), si\(y = -1\).
- Contestar
-
\((−40,−1)\)
\(y+7−x=0\), si\(x = *\)
\(2x+31y−3=0\), si\(x=a\)
- Contestar
-
\((a, \dfrac{3-2a}{31})\)
\(436x+189y=881\), si\(x=−4231\)
\(y=6(x−7)\), si\(x=2\)
- Contestar
-
\((2,−30)\)
\(y=2(4x+5)\), si\(x=−1\)
\(5y=9(x−3)\), si\(x=2\)
- Contestar
-
\((2, -\dfrac{9}{5})\)
\(3y=4(4x+1)\), si\(x=−3\)
\(−2y=3(2x−5)\), si\(x=6\)
- Contestar
-
\((6, -\dfrac{21}{2})\)
\(−8y=7(8x+2)\), si\(x=0\)
\(b=4a−12\), si\(a=−7\)
- Contestar
-
\((−7,−40)\)
\(b=−5a+21\), si\(a=−9\)
\(4b−6=2a+1\), si\(a=0\)
- Contestar
-
\((0, \dfrac{7}{4})\)
\(−5m+11=n+1\), si\(n=4\)
\(3(t+2)=4(s−9)\), si\(s=1\)
- Contestar
-
\((1, -\dfrac{38}{3})\)
\(7(t−6)=10(2−s)\), si\(s=5\)
\(y=0x+5\), si\(x=1\)
- Contestar
-
\((1,5)\)
\(2y=0x−11\), si\(x=−7\)
\(−y=0x+10\), si\(x=3\)
- Contestar
-
\((3,−10)\)
\(−5y=0x−1\), si\(x=0\)
\(y=0(x−1)+6\), si\(x=1\)
- Contestar
-
\((1,6)\)
\(y=0(3x+9)−1\), si\(x=12\)
Un examen de las velocidades ganadoras en la carrera automovilística Indianapolis 500 de 1961 a 1970 produce la ecuación\(y=1.93x+137.60\), donde\(x\) está el número de años a partir de 1960 y\(y\) es la velocidad ganadora. Se utilizaron métodos estadísticos para obtener la ecuación y, para un año determinado, la ecuación sólo da la velocidad aproximada de ganancia. Usa la ecuación\(y=1.93x+137.60\) para encontrar la velocidad ganadora aproximada en
- 1965
- 1970
- 1986
- 1990
- Contestar
-
(a) Aproximadamente 147 mph usando\((5,147.25)\)
(b) Aproximadamente 157 mph usando\((10,156.9)\)
(c) Aproximadamente 188 mph usando\((26,187.78)\)
(d) Aproximadamente 196 mph usando\((30,195.5)\)
En la teoría de la electricidad, la ley de Ohm relaciona la corriente eléctrica con el voltaje por la ecuación\(y=0.00082x\), donde\(x\) está el voltaje en voltios y\(y\) es la corriente en amperios. Esta ecuación se encontró por métodos estadísticos y para un voltaje dado solo rinde un valor aproximado para la corriente. Utilice la ecuación\(y=0.00082x\) para encontrar la corriente aproximada para un voltaje de
- 6 voltios
- 10 voltios
Se han utilizado métodos estadísticos para obtener una relación entre el número real y el número reportado de submarinos alemanes hundidos cada mes por la Armada de Estados Unidos en la Segunda Guerra Mundial. La ecuación que expresa el número aproximado de hundimientos reales,\(y\), para un número dado de hundimientos reportados,\(x\), es\(y=1.04x+0.76\). Encuentra el número aproximado de hundimientos reales de submarinos alemanes si el número reportado de hundimientos es
- 4
- 9
- 10
- Contestar
-
(a) Aproximadamente 5 hundimientos usando\((4,4.92)\)
(b) Aproximadamente 10 hundimientos usando\((9,10.12)\)
(c) Aproximadamente 11 hundimientos usando\((10,11.16)\)
Se han utilizado métodos estadísticos para obtener una relación entre el peso del corazón (en miligramos) y el peso corporal (en miligramos) de descendencia diabética de 10 meses de edad de ratones machos cruzados. La ecuación que expresa el peso corporal aproximado para un peso cardíaco dado es\(y=0.213x−4.44\). Encuentra el peso corporal aproximado para un peso cardíaco de
- 210 mg
- 245 mg
Se han utilizado métodos estadísticos para producir la ecuación\(y=0.176x−0.64\). Esta ecuación da el recuento aproximado de glóbulos rojos (en millones) de la sangre de un perro,\(y\), para un volumen de células empaquetadas dado (en milímetros),\(x\). Encuentre el recuento aproximado de glóbulos rojos para un volumen de células empaquetadas de
- 40 mm
- 42 mm
- Contestar
-
(a) Aproximadamente 6.4 usando\((40,6.4)\)
(b) Aproximadamente 4.752 usando\((42,7.752)\)
Una máquina industrial puede funcionar a diferentes velocidades. La máquina también produce artículos defectuosos, y el número de artículos defectuosos que produce parece estar relacionado con la velocidad a la que la máquina está funcionando. Los métodos estadísticos encontraron que la ecuación\(y=0.73x−0.86\) es capaz de dar el número aproximado de artículos defectuosos,\(y\), para una velocidad de máquina dada,\(x\). Utilice esta ecuación para encontrar el número aproximado de artículos defectuosos para una velocidad de máquina de
- 9
- 12
Una empresa informática ha encontrado, utilizando técnicas estadísticas, que existe una relación entre los puntajes de las pruebas de aptitud de los trabajadores de la línea de montaje y su productividad. Utilizando datos acumulados a lo largo de un periodo de tiempo,\(y=0.89x−41.78\) se derivó la ecuación. El\(x\) representa una puntuación de prueba de aptitud y\(y\) el número aproximado correspondiente de artículos ensamblados por hora. Estimar el número de ítems producidos por un trabajador con una puntuación de aptitud de
- 80
- 95
- Contestar
-
a) Aproximadamente 29 artículos utilizando\((80,29.42)\)
(b) Aproximadamente 43 elementos que utilizan\((95,42.77)\)
Los químicos, haciendo uso de técnicas estadísticas, han podido expresar el peso aproximado del bromuro de potasio,\(W\), que se disolverá en 100 gramos de agua a\(T\) grados centígrados. La ecuación que expresa esta relación es\(W=0.52T+54.2\). Utilice esta ecuación para predecir el peso del bromuro de potasio que se disolverá en 100 gramos de agua que se calienta a una temperatura de
- 70 grados centígrados
- 95 grados centígrados
El departamento de mercadotecnia de una gran empresa ha podido expresar la relación entre la demanda de un producto y su precio mediante técnicas estadísticas. El departamento encontró, al analizar estudios realizados en seis diferentes áreas del mercado, que la ecuación que da la demanda aproximada de un producto (en miles de unidades) por un precio determinado (en centavos) es\(y=−14.15x+257.11\). Encuentra el número aproximado de unidades demandadas cuando el precio es
- $0.12
- $0.15
- Contestar
-
(a) Aproximadamente 87 unidades usando\((12,87.31)\)
(b) Aproximadamente 45 unidades usando\((15,44.86)\)
El manejo de un programa de lectura rápida afirma que la ganancia aproximada de velocidad (en palabras por minuto)\(G\),, está relacionada con el número de semanas pasadas en su programa,\(W\), viene dada por la ecuación\(G=26.68W−7.44\). Predecir la ganancia aproximada de velocidad para un estudiante que ha gastado
- 3 semanas en el programa
- 10 semanas en el programa
Ejercicios para la revisión
Encuentra el producto. \((4x−1)(3x+5)\).
- Contestar
-
\(12x^2+17x−5\)
Encuentra el producto. \((5x+2)(5x−2)\)
Resuelve la ecuación\(6[2(x−4)+1]=3[2(x−7)]\).
- Contestar
-
\(x=0\)
Resolver la desigualdad\(−3a−(a−5)≥a+10\).
Resolver la desigualdad compuesta\(−1<4y+11<27\).
- Contestar
-
\(−3<y<4\)


