6.3: Factorización de un Monomio a partir de un Polinomio
- Page ID
- 112108
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El proceso de factorización
Introducimos el proceso de factorizar un monomio a partir de un polinomio examinando un problema: Supongamos que ese\(12x^2+20x\) es el producto y uno de los factores es\(4x\). Para encontrar el otro factor podríamos configurar el problema de esta manera:
\(4x \cdot () = 12x^2 + 20x\)
Dado que el producto\(12x^2 + 20x\) consta de dos términos, la expresión multiplicar\(4x\) debe constar de dos términos, ya que, por la propiedad distributiva
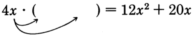
Ahora vemos que este problema es simplemente una extensión de encontrar los factores de un monomio.
\ (\ begin {array} {Flushleft}
\ text {1er término:} &4x () &=&12x^2&\ text {2do término:} &4x () &=&20x\
& () &=&\ dfrac {12x^2} {4x} && () &=&\ dfrac {20x} {4x}\
& () &=&3x&=&& () &=&5\\
\ end {array}\)
Por lo tanto,\(4x \cdot (3x+5) = 12x^2 + 20x\)
Por lo general, estas divisiones se pueden hacer mentalmente y los términos del factor se rellenan directamente.
Conjunto de Muestras A
El producto es\(3x^7-2x^6+4x^5-3x^4\) y un factor es\(x^4\). Encuentra el otro factor.
Tenemos el problema: ¿\(x^4\)tiempos “qué expresión” rinde\(3x^7-2x^6+4x^5-3x^4\)? Matemáticamente,
\(x^4 \cdot () = 3x^7-2x^6+4x^5-3x^4\)
Dado que hay cuatro términos en el producto, debe haber cuatro términos dentro de los paréntesis. Para encontrar cada uno de los cuatro términos, dividiremos (mentalmente) cada término del producto por\(x^4\). El cociente resultante será el término necesario del factor.
\ (\ begin {array} {Flushleft}
\ text {1er término:} &\ dfrac {3x^7} {x^4} &=&3x^ {7-4} =3x^3&\ text {Lugar} 3x^3\ texto {en la posición 1sdt en el ()}\\
\ text {2do término:} &\ dfrac {-2x^6} {x^4} &=&-2x^2&\ text {Colocar} -2x^2\ text {en la 2da posición en la ()}\\
\ text {3er término:} &\ dfrac {4x^5} {x^4} &=&4x&\ text {Colocar} 4x\ text {en la 3ª posición en el ()}\\
\ text {4to término:} &\ dfrac {-3x^4} {x^4} &=&-3&\ text {Lugar} -3\ text {en la 4ª posición en el ()}\\
\ end {array}\)
Por lo tanto, el otro factor es\(3x^3-2x^2+4x-3\).
Este resultado se puede verificar aplicando la propiedad distributiva.
\(x^4 \cdot (3x^3-2x^2+4x-3) = 3x^7-2x^6+4x^5-3x^4\). ¿Es esto correcto?
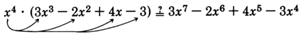
\(3x^{4+3} -2x^{4+2} + 4x^{4+1} = 3x^7 - 2x^6 + 4x^5 - 3x^4\)¿Es esto correcto?
\(3x^7 - 2x^6 + 4x^5 - 3x^4 = 3x^7 - 2x^6 + 4x^5 - 3x^4\)Sí, esto es correcto.
Por lo tanto,
\(x^4 \cdot (3x^3-2x^2+4x-3) = 3x^7-2x^6+4x^5-3x^4\)
Nuevamente, si las divisiones se pueden realizar mentalmente, el proceso puede proceder muy rápido.
El producto es\(10x^3y^6 + 15x^3y^4 - 5x^2y^4\) y un factor es\(5x^2y^4\). Encuentra el otro factor.
\(5x^2y^4 \cdot ( ) = 10x^3y^6 + 15x^3y^4 - 5x^2y^4\)
Dado que hay tres términos en el producto, debe haber tres términos dentro de los paréntesis. Para encontrar cada uno de estos tres términos, dividiremos cada término del producto por\(5x^2y^4\).
\ (\ begin {array} {Flushleft}
\ text {1er término:} &\ dfrac {10x^3y^6} {5x^2y^4} &=&2xy^2&\ text {Coloque el} 2xy^2\ text {en la 1ª posición en el ()}\\
\ text {2do término:} &\ dfrac {5x^3y4} {^2y^4} &=&3x&\ text {Coloca el} 3x\ text {en la 2da posición en el ()}\\
\ text {3er término:} &\ dfrac {-5x^2y^4} {5x^2y^4} &=&-1&\ text {Coloque el} -1\ text {en la 3ª posición en la ()}
\ end {array}\)
El otro factor es\(2xy^2 + 3x - 1\), y
\(5x^2y^4 \cdot (2xy^2 + 3x - 1) = 10x^3y^6 + 15x^3y^4 - 5x^2y^4\)
El producto es\(-4a^2-b^3+2c\) y un factor es\(-1\). Encuentra el otro factor.
\(-1( ) = -4a^2-b^3+2c\)
Dado que hay tres términos en el producto, debe haber tres términos dentro de los paréntesis. Dividiremos (mentalmente) cada término del producto por\(-1\)
\ (\ begin {array} {Flushleft}
\ text {1er término:} &\ dfrac {-4a^2} {-1} &=&4a^2&\ text {Lugar} 4a^2\ text {en la 1ª posición dentro del ()}\
\ texto {2do término:} &\ dfrac {-b^3} {-1} &=&b^3&\ text {Coloca} b^3\ text {en la 2da posición dentro de la ()}\\
\ text {3er término:} &\ dfrac {2c} {-1} &=&-2c&\ text {Colocar} -2c\ text {en la 3ª posición dentro de la ()}
\ end {array}\)
El otro factor es\(4a^2+b^3-2c\), y
\(-1(4a^2+b^3-2c) = -4a^2-b^3+2c\)
Sin escribir el\(-1\), obtenemos
\(-(4a^2+b^3-2c) = -4a^2-b^3+2c\)
El producto es\(-3a^2b^5 - 15a^3b^2 + 9a^2b^2\) y un factor es\(-3a^2b^2\). Encuentra el otro factor.
\(-3a^2b^2( ) = -3a^2b^5-15a^3b^2+9a^2b^2\)
Dividiendo mentalmente cada término del trinomio original por\(-3a^2b^2\), obtenemos\(b^3 + 5a - 3\) como el otro factor, y
\(-3a^2b^2(b^3 + 5a - 3) = -3a^2b^5 - 15a^3b^2 + 9a^2b^2\).
Conjunto de práctica A
El producto es\(3x^2 - 6x\) y un factor es\(3x\). Encuentra el otro factor.
- Contestar
-
\(x-2\)
El producto es\(5y^4 + 10y^3 - 15y^2\) y un factor es\(5y^2\). Encuentra el otro factor.
- Contestar
-
\(y^2 + 2y - 3\)
El producto es\(4x^5y^3 - 8x^4y^4 + 16x^3y^5 + 24xy^7\) y un factor es\(4xy^3\). Encuentra el otro factor.
- Contestar
-
\(x^4 - 2x^3y + 4x^2y^2 + 6y^4\)
El producto es\(-25a^4-35a^2+5\) y un factor es\(-5\). Encuentra el otro factor.
- Contestar
-
\(5a^4+7a^2-1\)
El producto es\(-a^2 + b^2\) y un factor es\(-1\). Encuentra el otro factor.
- Contestar
-
\(a^2-b^2\)
Ejercicios
Para los siguientes problemas, la primera cantidad representa el producto y la segunda cantidad un factor. Encuentra el otro factor.
\(4x+10, 2\)
- Contestar
-
\(2x+5\)
\(6y+18, 3\)
\(5x+25, 5\)
- Contestar
-
\(x+5\)
\(16a+64, 8\)
\(3a^2 + 9a, 3a\)
- Contestar
-
\(a+3\)
\(14b^2+16b, 2b\)
\(21x^2+28x, 7x\)
- Contestar
-
\(3x+4\)
\(45y^2+50y, 5y\)
\(18a^2-4a, 2a\)
- Contestar
-
\(9a−2\)
\(20a^2 - 12a, 4a\)
\(7x^2 - 14x, 7x\)
- Contestar
-
\(x−2\)
\(6y^2 - 24y, 6y\)
\(8a^2 + 4a, 4a\)
- Contestar
-
\(2a+1\)
\(26b^2 + 13b, 13b\)
\(9x^2 + 6x + 18, 6\)
- Contestar
-
\(\dfrac{3}{2}x^2 + x + 3\)
\(12b^2 + 16b + 20, 4\)
\(21x^2 + 7x - 14, 7\)
- Contestar
-
\(3x^2 + x - 2\)
\(35x^2 + 40x - 5, 5\)
\(14y^2 - 28y + 14, 14\)
- Contestar
-
\(y^2 - 2y + 1\)
\(36a^2 - 16a + 12, 4\)
\(4y^2 - 10y - 12, 2\)
- Contestar
-
\(2y^2 - 5y - 6\)
\(6b^2 - 6b - 3, 3\)
\(18x^3 + 20x, 2x\)
- Contestar
-
\(9x^2 + 10\)
\(40y^3 + 24y, 4y\)
\(16x^3 - 12x^2, 4x^2\)
- Contestar
-
\(4x−3\)
\(11x^3 - 11x + 11, 11\)
\(10a^3 + 12a^2 + 16a + 8, 2\)
- Contestar
-
\(5a^3 + 6a^2 + 8a + 4\)
\(14b^3 + 16b^2 + 26b + 30, 2\)
\(8a^3 - 4a^2 - 12a + 16, 4\)
- Contestar
-
\(2a^3 - a^2 - 3a + 4\)
\(25x^3 - 30x^2 + 15x - 10, 5\)
\(4x^6 + 16x^4 - 16x, 4x\)
- Contestar
-
\(x^5 + 4x^3 - 4\)
\(9a^5 + 6a^5 - 18a^4 + 24a^2, 3a^2\)
\(10x^3 - 35x^2, 5x^2\)
- Contestar
-
\(2x−7\)
\(12x^3y^5 + 20x^3y^2, 4x^3y^2\)
\(10a^4b^3 + 4a^3b^4, 2a^3b^3\)
- Contestar
-
\(5a+2b\)
\(8a^3b^6c^8 + 12a^2b^7c^6 - 16a^2b^7c^5, 4a^2b^5c^5\)
\(4x^5y^4+x^2+x, x\)
- Contestar
-
\(4x^4y^4+x+1\)
\(14a^5b^2 - 3a^4b^4 + 7a^3, a^3\)
\(64a^5b^3c^{11} + 56a^4b^4c^{10} - 48a^3b^5c^9 - 8a^3b^2c^5, 8a^3b^2c^5\)
- Contestar
-
\(8a^2bc^6 + 7ab^2c^5 - 6b^3c^4 - 1\)
\(3h^3b^2 - 2h^6b^3 - 9h^2b + hb, hb\)
\(5a + 10, -5\)
- Contestar
-
\(−a−2\)
\(6b+8, −2\)
\(8x^2 + 12x, -4x\)
- Contestar
-
\(−2x−3\)
\(20a^2b^2-10a^2, -10a^2\)
\(a+b, −1\)
- Contestar
-
\(−a−b\)
\(x+y, −1\)
\(a−b+c, −1\)
- Contestar
-
\(−a+b−c\)
\(2x+4y−z, −1\)
\(−a−b−c, −1\)
- Contestar
-
\(a+b+c\)
\(x^2-x+1, -1\)
Ejercicios para la revisión
¿Cuántos\(4y^2\) hay adentro\(24x^2y^3\)?
- Contestar
-
\(6x^2y\)
Encuentra el producto\((2y-3)^2\).
Resolver\(2(2a−1)−a=7\).
- Contestar
-
\(a=3\)
Dado que\(3m^2n\) es un factor de\(12m^3n^4\), encontrar el otro factor.


