1.6: Exponentes y Raíces Cuadradas

Última actualización
Guardar como PDF

Page ID: 110108

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Interpreta la notación exponencial con exponentes enteros positivos.
Calcular la potencia$n$ th de un número real.
Calcular el valor exacto y aproximado de la raíz cuadrada de un número real.

Notación exponencial y exponentes enteros positivos

Si un número se repite como factor numerosas veces, entonces podemos escribir el producto en una forma más compacta usando notación exponencial. Por ejemplo,

$5\cdot 5\cdot 5\cdot 5=5^{4}$

La base es el factor, y el exponente entero positivo indica el número de veces que la base se repite como factor. En el ejemplo anterior, la base es$5$ y el exponente es$4$. En general, si$a$ es la base la que se repite como factor$n$ veces, entonces

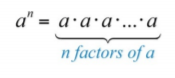$Captura de pantalla (971) .png$

Figura$\PageIndex{1}$

Cuando el exponente es$2$, llamamos cuadrado al resultado. Por ejemplo,

$3^{2}=3\cdot 3=9$

El número$3$ es la base y el entero$2$ es el exponente. La notación se$3^{2}$ puede leer de dos maneras: “tres al cuadrado” o “$3$elevado a la segunda potencia”. La base puede ser cualquier número real.

Es importante estudiar la diferencia entre las formas en que se calculan los dos últimos ejemplos. En el ejemplo$(−7)^{2}$, la base es$−7$ como lo indican los paréntesis. En el ejemplo$−5^{2}$, la base es$5$, no$−5$, por lo que sólo la$5$ es cuadrada y el resultado sigue siendo negativo. Para ilustrar esto, escribe

$-5^{2}=-1\cdot 5^{2}=-1\cdot 5\cdot 5=-25$

Esta sutil distinción es muy importante porque determina el signo del resultado.

La notación textual para los exponentes generalmente se denota usando el$(^)$ símbolo de intercalación de la siguiente manera:

$\begin{aligned}8^{2}&=8\wedge 2=8*8=64 \\ -5.1^{2}&=-5.1\wedge 2=-5.1*5.1=-26.01 \end{aligned}$

El cuadrado de un entero se llama cuadrado perfecto. La capacidad de reconocer cuadrados perfectos es útil en nuestro estudio del álgebra. Los cuadrados de los enteros de$1$ a$15$ deben ser memorizados. A continuación se muestra una lista parcial de cuadrados perfectos:

$\{0,1,4,9,16,25,36,49,64,81,100,121,144,169,196,225,...\}$

Ejercicio$\PageIndex{1}$

Simplificar

$(−12)^{2}$.

Contestar: $144$

Cuando el exponente es$3$ llamamos al resultado un cubo. Por ejemplo,

$3^{3}=3\cdot 3\cdot 3=27$

La notación se$3^{3}$ puede leer de dos maneras: “tres cubos” o “$3$elevada a la tercera potencia”. Como antes, la base puede ser cualquier número real.

Tenga en cuenta que el resultado de cubicar un número negativo es negativo. El cubo de un entero se llama un cubo perfecto. La capacidad de reconocer cubos perfectos es útil en nuestro estudio del álgebra. Los cubos de los enteros de$1$ a$10$ deben ser memorizados. A continuación se muestra una lista parcial de cubos perfectos:

$\{0,1,8,27,64,125,216,343,512,729,1000,...\}$

Ejercicio$\PageIndex{2}$

Simplificar$(−2)^{3}$.

Contestar: $-8$

Si el exponente es mayor que$3$, entonces la notación a se lee “a elevada a la potencia$n$ th”.

$\begin{aligned} 10^{6}&=10\cdot 10\cdot 10\cdot 10\cdot 10\cdot 10=1,000,000 \\ (-1)^{4}&=(-1)(-1)(-1)(-1)=1 \\ \left(\frac{1}{3} \right)^{5}&=\frac{1}{3}\cdot \frac{1}{3}\cdot \frac{1}{3}\cdot \frac{1}{3}\cdot \frac{1}{3} =\frac{1}{243} \end{aligned}$

Observe que el resultado de una base negativa con un exponente par es positivo. El resultado de una base negativa con un exponente impar es negativo. Estos hechos a menudo se confunden cuando se trata de números negativos. Estudie cuidadosamente los siguientes cuatro ejemplos:

Mesa$\PageIndex{1}$
La base es$(-2)$	La base es$2$
\ ((-2)\) ">$\begin{array}{c}{(-2)^{4}=(-2)\cdot (-2)\cdot (-2)\cdot (-2)=+16} \\ {(-2)^{3}=(-2)\cdot (-2)\cdot (-2)=-8} \end{array}$	\ (2\) ">$\begin{array}{c}{-2^{4}=-2\cdot 2\cdot 2\cdot 2=-16}\\{-2^{3}=-2\cdot 2\cdot 2=-8} \end{array}$

Los paréntesis indican que el número negativo se va a utilizar como base.

Ejemplo$\PageIndex{1}$

Calcular:

$\left(-\frac{1}{3} \right)^{3}$
$\left(-\frac{1}{3} \right)^{4}$

Solución:

La base es$−\frac{1}{3}$ para ambos problemas.

a. Utilizar la base como factor tres veces.

$\begin{aligned} \left(-\frac{1}{3} \right)^{3}&=\left(-\frac{1}{3} \right)\left(-\frac{1}{3} \right)\left(-\frac{1}{3} \right) \\ &=-\frac{1}{27} \end{aligned}$

b. Utilizar la base como factor cuatro veces.

$\begin{aligned} \left(-\frac{1}{3} \right)^{4}&=\left(-\frac{1}{3} \right)\left(-\frac{1}{3} \right)\left(-\frac{1}{3} \right)\left(-\frac{1}{3} \right) \\ &=+\frac{1}{81} \end{aligned}$

Respuesta:

a.$-\frac{1}{27}$; b.$\frac{1}{81}$

Ejercicio$\PageIndex{3}$

Simplificar:

$−10^{4}$y$(−10)^{4}$.

Contestar: $−10,000$y$10,000$

Raíz cuadrada de un número real

Piense en encontrar la raíz cuadrada de un número como la inversa de cuadrar un número. Es decir, para determinar la raíz cuadrada de$25$ la pregunta es: “¿Qué número al cuadrado es igual$25$?” En realidad, hay dos respuestas a esta pregunta,$5$ y$−5$.

$5^{2}=25\quad\text{and}(-5)^{2}=25$

Cuando se le pide la raíz cuadrada de un número, nos referimos implícitamente a la raíz cuadrada principal (no negativa). Por lo tanto, tenemos,

$\sqrt{a^{2}}=a$, si$a\geq 0$ o más generalmente$\sqrt{a^{2}}=|a|$

A modo de ejemplo$\sqrt{25}=5$,, que se lee “raíz cuadrada de$25$ iguales”$5$. El símbolo$√$ se llama el signo radical y$25$ se llama radicando. La notación textual alternativa para raíces cuadradas sigue:

$\sqrt{16}=text{sqrt}(16)=4$

También vale la pena señalar que

$\sqrt{1}=1\quad\text{and}\quad\sqrt{0}=0$

Este es el caso porque$1^{2}=1$ y$0^{2}=0$.

Ejemplo$\PageIndex{2}$

Simplificar:

$\sqrt{10,000}$.

Solución:

$10,000$es un cuadrado perfecto porque$100⋅100=10,000$.

$\begin{aligned} \sqrt{10,000}&=\sqrt{(100)^{2}} \\ &=100 \end{aligned}$

Respuesta:

$100$

Ejemplo$\PageIndex{3}$

Simplificar:

$\sqrt{\frac{1}{9}}$.

Solución:

Aquí notamos que$\frac{1}{9}$ es un cuadrado porque$\frac{1}{3}⋅\frac{1}{3}=\frac{1}{9}$.

$\begin{aligned} \sqrt{\frac{1}{9}}&=\sqrt{\left(\frac{1}{3} \right)^{2}} \\ &=\frac{1}{3} \end{aligned}$

Respuesta:

$\frac{1}{3}$

Dado$a$ y$b$ como números reales positivos, utilice la siguiente propiedad para simplificar las raíces cuadradas cuyos radicandos no son cuadrados:

$\sqrt{a\cdot b}=\sqrt{a}\cdot\sqrt{b}$

La idea es identificar el factor cuadrado más grande del radicando y luego aplicar la propiedad que se muestra arriba. A modo de ejemplo, para simplificar$\sqrt{8}$ aviso que no$8$ es un cuadrado perfecto. Sin embargo,$8=4⋅2$ y por lo tanto tiene un factor cuadrado perfecto distinto de$1$. Aplicar la propiedad de la siguiente manera:

$\begin{aligned} \sqrt{8}&=\sqrt{4\cdot 2} \\ &=\color{Cerulean}{\sqrt{4}}\color{black}{\cdot\sqrt{2}} \\ &=\color{Cerulean}{2}\color{black}{\cdot\sqrt{2}}\\&=2\sqrt{2} \end{aligned}$

Aquí$2\sqrt{2}$ hay un número irracional simplificado. A menudo se le pide que encuentre una respuesta aproximada redondeada a un cierto decimal. En ese caso, usa una calculadora para encontrar la aproximación decimal usando ya sea el problema original o el equivalente simplificado.

$\sqrt{8}=2\sqrt{2}\approx 2.83$

En una calculadora, inténtalo$2.83\wedge 2$. ¿Qué esperas? ¿Por qué la respuesta no es la que esperarías?

Es importante mencionar que el radicando debe ser positivo. Por ejemplo,$\sqrt{−9}$ es indefinido ya que no hay un número real que al cuadrar sea negativo. Intenta tomar la raíz cuadrada de un número negativo en tu calculadora. ¿Qué dice?

Nota

Tomar la raíz cuadrada de un número negativo se define más adelante en el curso.

Ejemplo$\PageIndex{4}$

Simplifica y da una respuesta aproximada redondeada a la centésima más cercana:

$\sqrt{75}$.

Solución:

El radicando se$75$ puede factorizar como$25 ⋅ 3$ donde el factor$25$ es un cuadrado perfecto.

$\begin{aligned} \sqrt{75}&=\sqrt{25\cdot 3}&\color{Cerulean}{The\:largest\:perfect\:square} \\ &=\color{Cerulean}{\sqrt{25}}\color{black}{\cdot\sqrt{3}}&\color{Cerulean}{factor\:of\:75\:is\:25.} \\ &=\color{Cerulean}{5}\color{black}{\cdot\sqrt{3}} \\ &=5\sqrt{3} &\color{Cerulean}{Exact\:answer} \\ &\approx 8.66 &\color{Cerulean}{Approximate\:answer} \end{aligned}$

Respuesta:

$\sqrt{75}\approx 8.66$

Como cheque, calcule (\ sqrt {75}\) y$5\sqrt{3}$ en una calculadora y verifique que ambos resultados sean aproximadamente$8.66$.

Ejemplo$\PageIndex{5}$

Simplificar:

$\sqrt{180}$.

Solución:

$\begin{aligned} \sqrt{180}&=\sqrt{36\cdot 5} \\ &=\color{Cerulean}{\sqrt{36}}\color{black}{\cdot\sqrt{5}} \\ &=\color{Cerulean}{6}\color{black}{\cdot\sqrt{5}} \\ &=6\sqrt{5} \end{aligned}$

Dado que la pregunta no pidió una respuesta aproximada, presentamos la respuesta exacta.

Respuesta:

$6\sqrt{5}$

Ejemplo$\PageIndex{6}$

Simplificar:

$-5\sqrt{162}$.

Solución:

$\begin{aligned} -5\sqrt{162}&=-5\cdot\sqrt{81\cdot 2} \\ &=-5\cdot\color{Cerulean}{\sqrt{81}}\color{black}{\cdot\sqrt{2}} \\ &=-5\cdot\color{Cerulean}{9}\color{black}{\cdot\sqrt{2}} \\ &=-45\cdot\sqrt{2} \\ &=-45\sqrt{2} \end{aligned}$

Respuesta:

$-45\sqrt{2}$

Ejercicio$\PageIndex{4}$

Simplifica y da una respuesta aproximada redondeada a la centésima más cercana:

$\sqrt{128}$.

Contestar: $8\sqrt{2}≈11.31$

Un triángulo rectángulo es un triángulo donde uno de los ángulos mide$90°$. El lado opuesto al ángulo recto es el lado más largo, llamado hipotenusa, y los otros dos lados se llaman piernas. Numerosas aplicaciones del mundo real involucran esta figura geométrica. El teorema de Pitágoras establece que dado cualquier triángulo rectángulo con patas de medición$a$ y$b$ unidades, el cuadrado de la medida de la hipotenusa c es igual a la suma de los cuadrados de las medidas de las piernas:$a^{2}+b^{2}=c^{2}$. Es decir, la hipotenusa de cualquier triángulo rectángulo es igual a la raíz cuadrada de la suma de los cuadrados de sus patas.

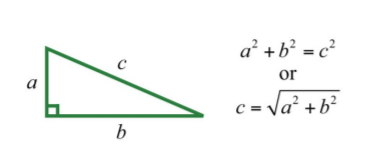$Captura de pantalla (973) .png$

Figura$\PageIndex{1}$

Ejemplo$\PageIndex{7}$

Si las dos patas de un triángulo rectángulo miden$3$ unidades y$4$ unidades, entonces encuentra la longitud de la hipotenusa.

Solución:

Dadas las longitudes de las patas de un triángulo rectángulo, usa la fórmula$c=\sqrt{a^{2}+b^{2}}$ para encontrar la longitud de la hipotenusa.

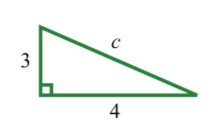$Captura de pantalla (974) .png$

Figura$\PageIndex{2}$

$\begin{aligned} c&=\sqrt{a^{2}+b^{2}} \\ c&=\sqrt{3^{2}+4^{2}} \\ &=\sqrt{9+16} \\ &=\sqrt{25} \\ &=5 \end{aligned}$

Respuesta:

$c=5$unidades

Al encontrar la hipotenusa de un triángulo rectángulo usando el teorema de Pitágoras, el radicando no siempre es un cuadrado perfecto.

Ejemplo$\PageIndex{8}$

Si las dos patas de un triángulo rectángulo miden$2$ unidades y$6$ unidades, encuentra la longitud de la hipotenusa.

Solución:

$Captura de pantalla (975) .png$

Figura$\PageIndex{3}$

$\begin{aligned} c&=\sqrt{a^{2}+b^{2}} \\ &=\sqrt{2^{2}+6^{2}} \\ &=\sqrt{4+36} \\ &=\sqrt{40} \\ &=\sqrt{4\cdot 10} \\&=\sqrt{4}\cdot\sqrt{10} \\ &=2\cdot\sqrt{10} \end{aligned}$

Respuesta:

$c=2\sqrt{10}$unidades

Claves para llevar

Cuando se usa notación exponencial$a^{n}$, la base$a$ se usa como factor$n$ veces.
Cuando el exponente es$2$, el resultado se llama cuadrado. Cuando el exponente es$3$, el resultado se llama cubo.
Memorizar los cuadrados de los enteros hasta$15$ y los cubos de los enteros hasta$10$. Serán utilizados a menudo a medida que avances en tu estudio del álgebra.
Cuando estén involucrados números negativos, tenga cuidado de asociar al exponente con la base correcta. Los paréntesis agrupan un número negativo elevado a alguna potencia.
Una base negativa elevada a una potencia par es positiva.
Una base negativa elevada a una potencia impar es negativa.
La raíz cuadrada de un número es un número que cuando se cuadra da como resultado el número original. La raíz cuadrada principal es la raíz cuadrada positiva.
Simplifique una raíz cuadrada buscando el factor cuadrado perfecto más grande del radicando. Una vez que se encuentre un cuadrado perfecto, aplique la propiedad$\sqrt{a⋅b}=\sqrt{a}⋅\sqrt{b}$, donde$a$ y no$b$ sean negativos, y simplifique.
Verifique las raíces cuadradas simplificadas calculando aproximaciones de la respuesta utilizando tanto el problema original como la respuesta simplificada en una calculadora para verificar que los resultados son los mismos.
Encuentra la longitud de la hipotenusa de cualquier triángulo rectángulo dadas las longitudes de las piernas usando el teorema de Pitágoras.

Ejercicio$\PageIndex{5}$ Square of a Number

Simplificar.

$10^{2}$
$12^{2}$
$(−9)^{2}$
$−12^{2}$
$11^{2}$
$(−20)^{2}$
$0^{2}$
$1^{2}$
$−(−8)^{2}$
$−(13)^{2}$
$(\frac{1}{2})^{2}$
$(−\frac{2}{3})^{2}$
$0.5^{2}$
$1.25^{2}$
$(−2.6)^{2}$
$−(−5.1)^{2}$
$(2\frac{1}{3})^{2}$
$(5\frac{3}{4})^{2}$

Contestar

1. $100$

3. $81$

5. $121$

7. $0$

9. $−64$

11. $\frac{1}{4}$

13. $.25$

15. $6.76$

17. $5\frac{4}{9}$

Ejercicio$\PageIndex{6}$ Square of a Number

Si$s$ es la longitud del lado de un cuadrado, entonces el área viene dada por$A=s^{2}$.

Determinar el área de un cuadrado dado que un lado mide$5$ pulgadas.
Determinar el área de un cuadrado dado que un lado mide$2.3$ pies.
Enumere todos los cuadrados de los enteros$0$ a través de$15$.
Enumere todos los cuadrados de los enteros de$−15$ a$0$.
Enumere los cuadrados de todos los números racionales del conjunto$\{0, \frac{1}{3}, \frac{2}{3}, 1, \frac{4}{3}, \frac{5}{3}, 2\}$.
Enumere los cuadrados de todos los números racionales del conjunto$\{0, \frac{1}{2}, 1, \frac{3}{2}, 2, \frac{5}{2}\}$.

Contestar

1. $25$pulgadas cuadradas

3. $\{0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225\}$

5. $\{0, \frac{1}{9}, \frac{4}{9}, 1, \frac{16}{9}, \frac{25}{9}, 4\}$

Ejercicio$\PageIndex{7}$ Integer Exponents

Simplificar.

$5^{3}$
$2^{6}$
$(−1)^{4}$
$(−3)^{3}$
$−1^{4}$
$(−2)^{4}$
$−7^{3}$
$(−7)^{3}$
$−(−3)^{3}$
$−(−10)^{4}$
$(−1)^{20}$
$(−1)^{21}$
$(−6)^{3}$
$−3^{4}$
$1^{100}$
$0^{100}$
$−(\frac{1}{2})^{3}$
$(\frac{1}{2})^{6}$
$(\frac{5}{2})^{3}$
$(−\frac{3}{4})^{4}$
Listar todos los cubos de los enteros$−5$ a través de$5$.
Listar todos los cubos de los enteros de$−10$ a$0$.
Enumere todos los cubos de los números racionales en el conjunto$\{−\frac{2}{3}, −\frac{1}{3}, 0, \frac{1}{3}, \frac{2}{3}\}$.
Enumere todos los cubos de los números racionales en el conjunto$\{−\frac{3}{7}, −\frac{1}{7}, 0, \frac{1}{7}, \frac{3}{7}\}$.

Responder

1. $125$

3. $1$

5. $−1$

7. $−343$

9. $27$

11. $1$

13. $−216$

15. $1$

17. $−\frac{1}{8}$

19. $\frac{12}{58}$

21. $\{−125, −64, −27, −8, −1, 0, 1, 8, 27, 64, 125\}$

23. $\{−\frac{8}{27}, −\frac{1}{27}, 0, \frac{1}{27}, \frac{8}{27}\}$

Ejercicio$\PageIndex{8}$ Square Root of a Number

Determinar la respuesta exacta en forma simplificada.

$\sqrt{121}$
$\sqrt{81}$
$\sqrt{100}$
$\sqrt{169}$
$−\sqrt{25}$
$−\sqrt{144}$
$\sqrt{12}$
$\sqrt{27}$
$\sqrt{45}$
$\sqrt{50}$
$\sqrt{98}$
$\sqrt{2000}$
$\sqrt{\frac{1}{4}}$
$\sqrt{\frac{9}{16}}$
$\sqrt{\frac{5}{9}}$
$\sqrt{\frac{8}{36}}$
$\sqrt{0.64}$
$\sqrt{0.81}$
$\sqrt{30^{2}}$
$\sqrt{15^{2}}$
$\sqrt{(−2)^{2}}$
$\sqrt{(−5)^{2}}$
$\sqrt{−9}$
$\sqrt{−16}$
$3\sqrt{16}$
$5\sqrt{18}$
$−2\sqrt{36}$
$−3\sqrt{32}$
$6\sqrt{200}$
$10\sqrt{27}$

Responder

1. $11$

3. $10$

5. $−5$

7. $2\sqrt{3}$

9. $3\sqrt{5}$

11. $7\sqrt{2}$

13. $\frac{1}{2}$

15. $5\sqrt{3}$

17. $0.8$

19. $30$

21. $2$

23. No es real

25. $12$

27. $−12$

29. $60\sqrt{2}$

Ejercicio$\PageIndex{9}$ Square Root of a Number

Aproximar lo siguiente a la centésima más cercana.

$\sqrt{2}$
$\sqrt{3}$
$\sqrt{10}$
$\sqrt{15}$
$2\sqrt{3}$
$5\sqrt{2}$
$−6\sqrt{5}$
$-4\sqrt{6}$
$\sqrt{79}$
$\sqrt{54}$
$−\sqrt{162}$
$−\sqrt{86}$
Si las dos patas de un triángulo rectángulo miden$6$ unidades y$8$ unidades, entonces encuentra la longitud de la hipotenusa.
Si las dos patas de un triángulo rectángulo miden$5$ unidades y$12$ unidades, entonces encuentra la longitud de la hipotenusa.
Si las dos patas de un triángulo rectángulo miden$9$ unidades y$12$ unidades, entonces encuentra la longitud de la hipotenusa.
Si las dos patas de un triángulo rectángulo miden$\frac{3}{2}$ unidades y$2$ unidades, entonces encuentra la longitud de la hipotenusa.
Si las dos patas de un triángulo rectángulo miden ambas$1$ unidades, entonces encuentra la longitud de la hipotenusa.
Si las dos patas de un triángulo rectángulo miden$1$ unidad y$5$ unidades, entonces encuentra la longitud de la hipotenusa.
Si las dos patas de un triángulo rectángulo miden$2$ unidades y$4$ unidades, entonces encuentra la longitud de la hipotenusa.
Si las dos patas de un triángulo rectángulo miden$3$ unidades y$9$ unidades, entonces encuentra la longitud de la hipotenusa.

Responder

1. $1.41$

3. $3.16$

5. $3.46$

7. $−13.42$

9. $8.89$

11. $−12.73$

13. $10$unidades

15. $15$unidades

17. $\sqrt{2}$unidades

19. $2\sqrt{5}$unidades

Ejercicio$\PageIndex{10}$ Discussion Board Topics

¿Por qué es el resultado de un exponente de$2$ llamado cuadrado? ¿Por qué es el resultado de un exponente de$3$ llamado cubo?
Investigar y discutir la historia del teorema de Pitágoras.
Investigar y discutir la historia de la raíz cuadrada.
Discutir la importancia de la raíz cuadrada principal.

Responder

1. Las respuestas pueden variar

3. Las respuestas pueden variar