5.1: Raíces y Radicales

Objetivos de aprendizaje

• Identificar y evaluar las raíces cuadradas y cúbicas.
• Determinar el dominio de las funciones que involucran raíces cuadradas y cúbicas.
• $n$Evaluar las raíces.
• Simplifique los radicales usando las reglas de producto y cociente para radicales.

Raíces cuadradas y cubitas

Recordemos que una raíz cuadrada ¹ de un número es un número que al multiplicarse por sí mismo produce el número original. Por ejemplo,$5$ es una raíz cuadrada de$25$, porque$5^{2} = 25$. Ya que$(−5)^{2} = 25$, podemos decir que$−5$ es una raíz cuadrada de$25$ también. Cada número real positivo tiene dos raíces cuadradas, una positiva y otra negativa. Por esta razón, utilizamos el signo radical$√$ para denotar la raíz cuadrada principal (no negativa) ² y un signo negativo frente al radical$−√$ para denotar la raíz cuadrada negativa.

$\begin{aligned} \sqrt { 25 } & = 5 \quad\quad\color{Cerulean} { Positive\: square \:root \:of \: 25} \\ - \sqrt { 25 } & = - 5 \quad\:\color{Cerulean} { Negative \:square\: root \:of\: 25} \end{aligned}$

Cero es el único número real con una raíz cuadrada.

$\sqrt { 0 } = 0 \text { because } 0 ^ { 2 } = 0$

Ejemplo$\PageIndex{1}$:

Evaluar.

1. $\sqrt { 121 }$
2. $- \sqrt { 81 }$

Solución

1. $\sqrt { 121 } = \sqrt { 11 ^ { 2 } } = 11$
2. $- \sqrt { 81 } = - \sqrt { 9 ^ { 2 } } = - 9$

Si el radicando ³, el número dentro del signo radical, se puede factorizar como el cuadrado de otro número, entonces la raíz cuadrada del número es aparente. En este caso, tenemos la siguiente propiedad:

$\sqrt { a ^ { 2 } } = a \quad \text { if } \quad a \geq 0$

O más generalmente,

$\sqrt { a ^ { 2 } } = | a | \quad \text { if } \quad a \in R$

El valor absoluto es importante porque$a$ puede ser un número negativo y el signo radical denota la raíz cuadrada principal. Por ejemplo,

$\sqrt { ( - 8 ) ^ { 2 } } = | -8| = 8$

Hacer uso del valor absoluto para asegurar un resultado positivo.

Ejemplo$\PageIndex{2}$:

Simplificar:$\sqrt { ( x - 2 ) ^ { 2 } }$.

Solución

Aquí la expresión de la variable$x − 2$ podría ser negativa, cero o positiva. Dado que el signo depende de la cantidad desconocida$x$, debemos asegurarnos de obtener la raíz cuadrada principal haciendo uso del valor absoluto.

$\sqrt { ( x - 2 ) ^ { 2 } } = | x - 2 |$

Respuesta:

$| x - 2 |$

La importancia del uso del valor absoluto en el ejemplo anterior es evidente cuando evaluamos utilizando valores que hacen que el radical sea negativo. Por ejemplo, cuando$x = 1$,

$\begin{aligned} \sqrt { ( x - 2 ) ^ { 2 } } & = | x - 2 | \\ & = | 1 - 2 | \\ & = | - 1 | \\ & = 1 \end{aligned}$

A continuación, considere la raíz cuadrada de un número negativo. Para determinar la raíz cuadrada de$−25$, debe encontrar un número que al cuadrado resulte en$−25$:

$\sqrt { - 25 } = \color{Cerulean}{?} \color{black}\quad{ \text { or }} \quad( \color{Cerulean}{?}\color{black}{ )} ^ { 2 } = - 25$

Sin embargo, cualquier número real al cuadrado siempre resulta en un número positivo. La raíz cuadrada de un número negativo se deja indefinida actualmente. Por ahora, vamos a decir que no$\sqrt { - 25 }$ es un número real. Por lo tanto, la función de raíz cuadrada ⁴ dada por no$f ( x ) = \sqrt { x }$ se define como un número real si los$x$ valores -son negativos. El valor más pequeño en el dominio es cero. Por ejemplo,$f ( 0 ) = \sqrt { 0 } = 0$ y$f ( 4 ) = \sqrt { 4 } = 2$. Recordemos la gráfica de la función de raíz cuadrada.

Figura$\PageIndex{1}$

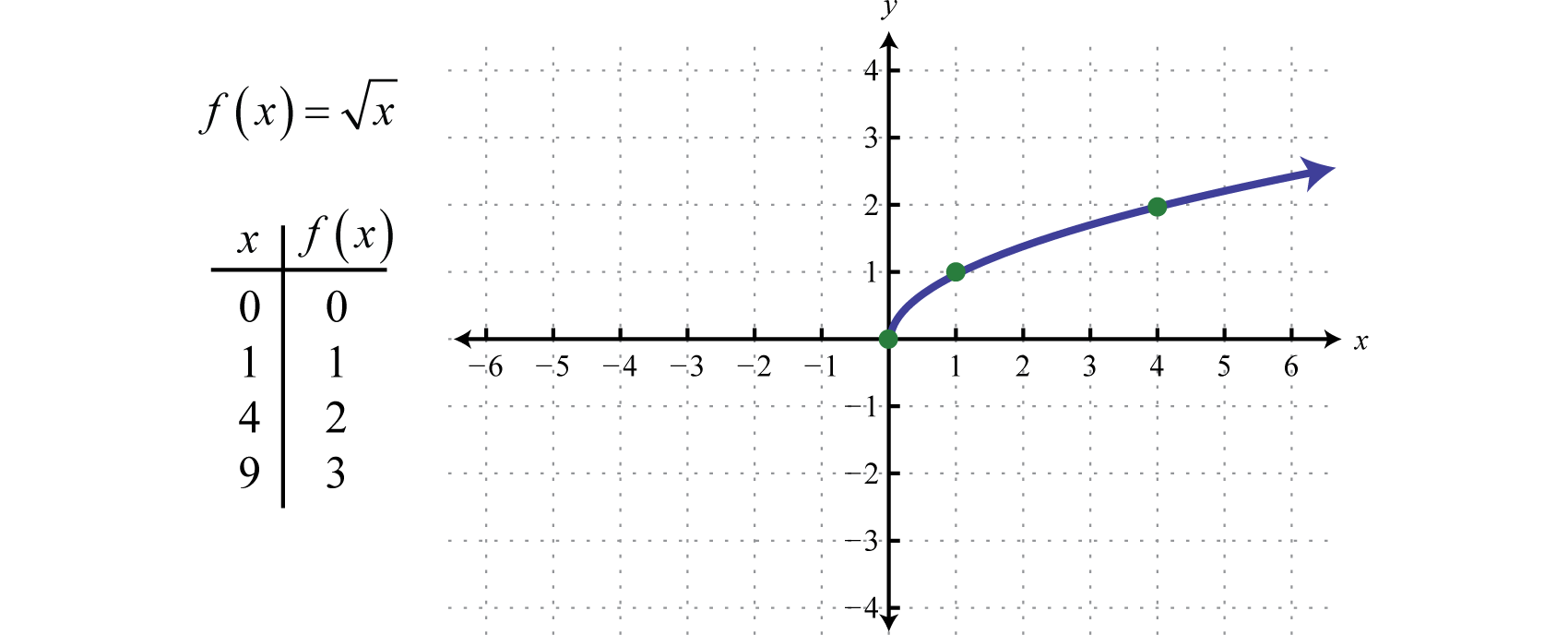
Tanto el dominio como el rango consisten en números reales mayores o iguales a cero:$[0, ∞)$. Para determinar el dominio de una función que involucra una raíz cuadrada observamos el radicando y encontramos los valores que producen resultados no negativos.

Ejemplo$\PageIndex{3}$:

Determinar el dominio de la función definida por$f ( x ) = \sqrt { 2 x + 3 }$.

Solución

Aquí está el radicando$2x + 3$. Esta expresión debe ser cero o positiva. En otras palabras,

$2 x + 3 \geq 0$

Resolver para$x$.

$\begin{aligned} 2 x + 3 & \geq 0 \\ 2 x & \geq - 3 \\ x & \geq - \frac { 3 } { 2 } \end{aligned}$

Respuesta:

Dominio:$\left[ - \frac { 3 } { 2 } , \infty \right)$

Una raíz cubo ⁵ de un número es un número que cuando se multiplica por sí mismo tres veces produce el número original. Además, denotamos una raíz cubo usando el símbolo$\sqrt [ 3 ] { }$, donde$3$ se llama el índice ⁶. Por ejemplo,

$\sqrt [ 3 ] { 64 } = 4 , \text { because } 4 ^ { 3 } = 64$

El producto de tres factores iguales será positivo si el factor es positivo y negativo si el factor es negativo. Por esta razón, cualquier número real tendrá sólo una raíz cúbica real. De ahí que no se apliquen los tecnicismos asociados a la raíz principal. Por ejemplo,

$\sqrt [ 3 ] { - 64 } = - 4 , \text { because } ( - 4 ) ^ { 3 } = - 64$

En general, dado cualquier número real$a$, tenemos la siguiente propiedad:

$\sqrt [ 3 ] { a ^ { 3 } } = a \quad \text { if } \quad a \in R$

Al simplificar las raíces cúbicas, busca factores que sean cubos perfectos.

Ejemplo$\PageIndex{4}$:

Evaluar.

1. $\sqrt [ 3 ] { 8 }$
2. $\sqrt [ 3 ] { 0 }$
3. $\sqrt [ 3 ] { \frac { 1 } { 27 } }$
4. $\sqrt [ 3 ] { - 1 }$
5. $\sqrt [ 3 ] { - 125 }$

Solución

1. $\sqrt [ 3 ] { 8 } = \sqrt [ 3 ] { 2 ^ { 3 } } = 2$
2. $\sqrt [ 3 ] { 0 } = \sqrt [ 3 ] { 0 ^ { 3 } } = 0$
3. $\sqrt [ 3 ] { \frac { 1 } { 27 } } = \sqrt [ 3 ] { \left( \frac { 1 } { 3 } \right) ^ { 3 } } = \frac { 1 } { 3 }$
4. $\sqrt [ 3 ] { - 1 } = \sqrt [ 3 ] { ( - 1 ) ^ { 3 } } = - 1$
5. $\sqrt [ 3 ] { - 125 } = \sqrt [ 3 ] { ( - 5 ) ^ { 3 } } = - 5$

Puede darse el caso de que el radicando no sea un cuadrado o cubo perfecto. Si un entero no es una potencia perfecta del índice, entonces su raíz será irracional. Por ejemplo,$\sqrt [ 3 ] { 2 }$ es un número irracional que se puede aproximar en la mayoría de las calculadoras usando el botón$\sqrt [ x ] { }$ raíz. Dependiendo de la calculadora, normalmente escribimos el índice antes de presionar el botón y luego el radicando de la siguiente manera:

$3 \quad\sqrt [ x ] {y }\quad2\quad=$

Por lo tanto, tenemos

$\sqrt [ 3 ] { 2 } \approx 1.260 , \quad \text { because } \quad 1.260 ^{\wedge} 3 \approx 2$

Dado que las raíces cúbicas pueden ser negativas, cero o positivas, no hacemos uso de ningún valor absoluto.

Ejemplo$\PageIndex{5}$:

Simplificar:$\sqrt [ 3 ] { ( y - 7 ) ^ { 3 } }$.

Solución

La raíz cúbica de una cantidad en cubos es esa cantidad.

$\sqrt [ 3 ] { ( y - 7 ) ^ { 3 } } = y - 7$

Respuesta:

$y-7$

Ejercicio$\PageIndex{1}$

Evaluar:$\sqrt [ 3 ] { - 1000 }$.

Responder

$=10$

www.youtube.com/V/B06NIS-3GIG

A continuación, considere la función de raíz cubo ⁷:

$f ( x ) = \sqrt [ 3 ] { x } \quad\color{Cerulean}{Cube\:root\:function.}$

Dado que la raíz cubo podría ser negativa o positiva, concluimos que el dominio consiste en todos los números reales. Esboce la gráfica trazando puntos. Elija algunos valores positivos y negativos para$x$, así como cero, y luego calcule los$y$ valores -correspondientes.

Mesa$\PageIndex{1}$

$x$	$f(x)$	$f ( x ) = \sqrt [ 3 ] { x }$	$\color{Cerulean}{Ordered\:Pairs}$
\ (x\) ">$-8$	\ (f (x)\) ">$\color{Cerulean}{-2}$	\ (f (x) =\ sqrt [3] {x}\) ">$f ( - 8 ) = \sqrt [ 3 ] { - 8 } = - 2$	\ (\ color {cerúleo} {Pedido\ :Pares}\) ">$(-8,-2)$
\ (x\) ">$-1$	\ (f (x)\) ">$\color{Cerulean}{-1}$	\ (f (x) =\ sqrt [3] {x}\) ">$f ( - 1 ) = \sqrt [ 3 ] { - 1 } = - 1$	\ (\ color {cerúleo} {Pedido\ :Pares}\) ">$(-1,-1)$
\ (x\) ">$0$	\ (f (x)\) ">$\color{Cerulean}{0}$	\ (f (x) =\ sqrt [3] {x}\) ">$f ( 0 ) = \sqrt [ 3 ] { 0 } = 0$	\ (\ color {cerúleo} {Pedido\ :Pares}\) ">$(0,0)$
\ (x\) ">$1$	\ (f (x)\) ">$\color{Cerulean}{1}$	\ (f (x) =\ sqrt [3] {x}\) ">$f ( 1 ) = \sqrt [ 3 ] { 1 } = 1$	\ (\ color {cerúleo} {Pedido\ :Pares}\) ">$(1,1)$
\ (x\) ">$8$	\ (f (x)\) ">$\color{Cerulean}{2}$	\ (f (x) =\ sqrt [3] {x}\) ">$f ( 8 ) = \sqrt [ 3 ] { 8 } = 2$	\ (\ color {cerúleo} {Pedido\ :Pares}\) ">$(8,2)$

Trace los puntos y dibuje la gráfica de la función de raíz cúbica.

Figura$\PageIndex{2}$

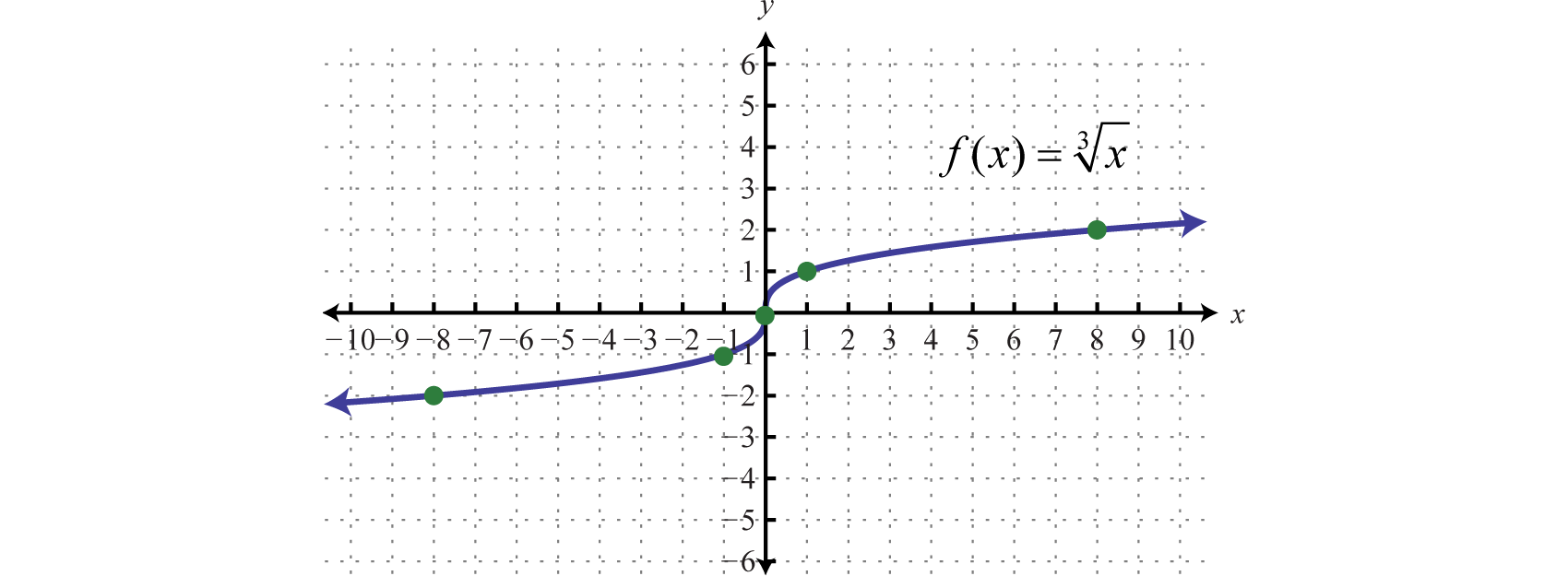
El gráfico pasa la prueba de línea vertical y de hecho es una función. Además, el rango consta de todos los números reales.

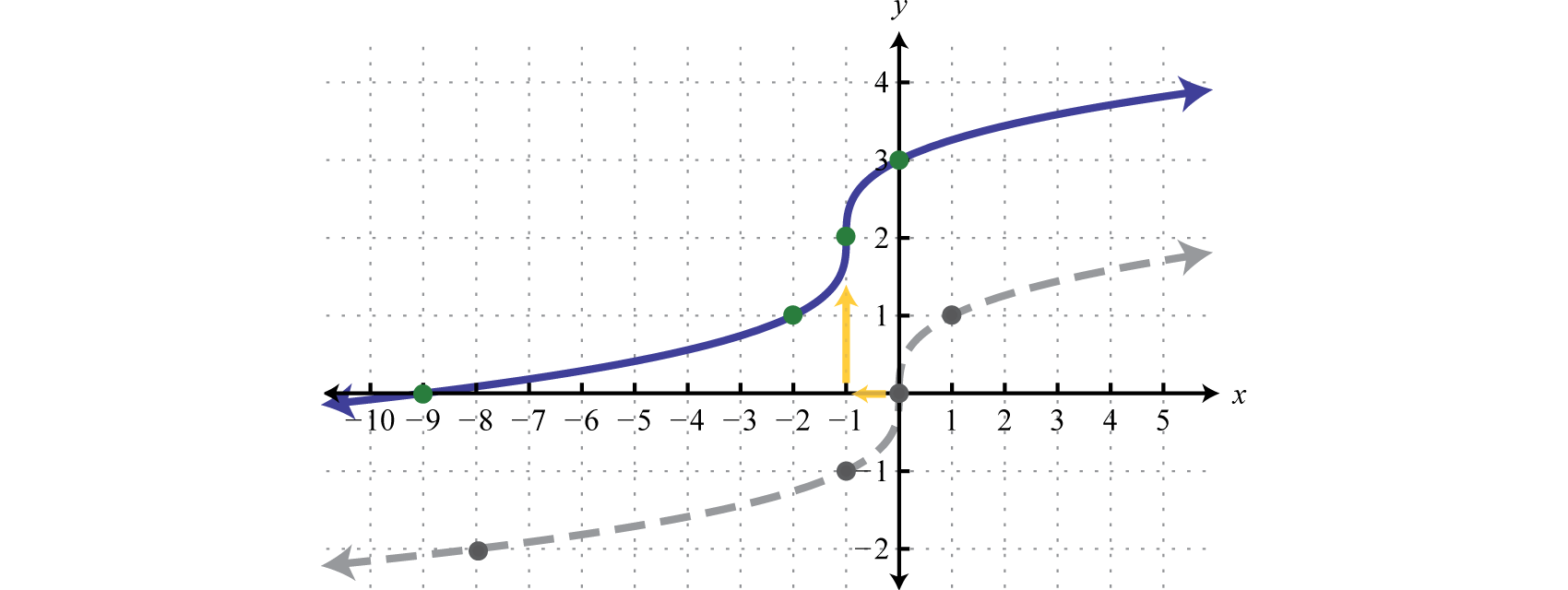
Ejemplo$\PageIndex{6}$:

Dado$g ( x ) = \sqrt [ 3 ] { x + 1 } + 2$, encontrar$g ( - 9 ) , g ( - 2 ) , g ( - 1 )$, y$g(0)$. Esbozar la gráfica de$g$.

Solución

Reemplazar$x$ con los valores dados.

Mesa$\PageIndex{2}$

$x$	$g(x)$	$g ( x ) = \sqrt [ 3 ] { x + 1 } + 2$	$\color{Cerulean}{Ordered\:Pairs}$
\ (x\) ">$-9$	\ (g (x)\) ">$\color{Cerulean}{0}$	\ (g (x) =\ sqrt [3] {x + 1} + 2\) ">$g ( \color{OliveGreen}{- 9}\color{black}{ )} = \sqrt [ 3 ] { \color{OliveGreen}{- 9}\color{black}{ +} 1 } + 2 = \sqrt [ 3 ] { - 8 } + 2 = - 2 + 2 = 0$	\ (\ color {cerúleo} {Pedido\ :Pares}\) ">$(-9,0)$
\ (x\) ">$-2$	\ (g (x)\) ">$\color{Cerulean}{1}$	\ (g (x) =\ sqrt [3] {x + 1} + 2\) ">$g ( \color{OliveGreen}{- 2}\color{black}{ )} = \sqrt [ 3 ] {\color{OliveGreen}{ - 2}\color{black}{ +} 1 } + 2 = \sqrt [ 3 ] { - 1 } + 2 = - 1 + 2 = 1$	\ (\ color {cerúleo} {Pedido\ :Pares}\) ">$(-2,1)$
\ (x\) ">$-1$	\ (g (x)\) ">$\color{Cerulean}{2}$	\ (g (x) =\ sqrt [3] {x + 1} + 2\) ">$g ( \color{OliveGreen}{- 1}\color{black}{ )} = \sqrt [ 3 ] { \color{OliveGreen}{- 1}\color{black}{ +} 1 } + 2 = \sqrt [ 3 ] { 0 } + 2 = 0 + 2 = 2$	\ (\ color {cerúleo} {Pedido\ :Pares}\) ">$(-1,2)$
\ (x\) ">$0$	\ (g (x)\) ">$\color{Cerulean}{3}$	\ (g (x) =\ sqrt [3] {x + 1} + 2\) ">$g ( \color{OliveGreen}{0}\color{black}{ )} = \sqrt [ 3 ] { \color{OliveGreen}{0}\color{black}{ +} 1 } + 2 = \sqrt [ 3 ] { 1 } + 2 = 1 + 2 = 3$	\ (\ color {cerúleo} {Pedido\ :Pares}\) ">$(0,3)$

También podemos bosquejar la gráfica utilizando las siguientes traducciones:

$\begin{array} { l } { y = \sqrt [ 3 ] { x } \quad\quad\quad\quad \color{Cerulean} { Basic\: cube \:root\: function } } \\ { y = \sqrt [ 3 ] { x + 1 } \quad \quad\:\color{Cerulean} { Horizontal\: shift\: left\: 1\: unit } } \\ { y = \sqrt [ 3 ] { x + 1 } + 2 \:\:\:\color{Cerulean} { Vertical\: shift\: up\: 2\: units } } \end{array}$

Respuesta:

Figura$\PageIndex{3}$

$n$th Raíces

Para cualquier entero$n ≥ 2$, definimos una raíz$n$ th ⁸ de un número real positivo como un número que cuando se eleva a la potencia$n$ th produce el número original. Dado cualquier número real no negativo$a$, tenemos la siguiente propiedad:

$\sqrt [ n ] { a ^ { n } } = a , \quad \text { if } \quad a \geq 0$

Aquí n se llama el índice y$a^{n}$ se llama el radicando. Además, podemos referirnos a toda la expresión$\sqrt [ n ] { A }$ como un radical ⁹. Cuando el índice es un número entero mayor o igual a$4$, decimos “cuarta raíz”, “quinta raíz”, y así sucesivamente. La raíz$n$ th de cualquier número es aparente si podemos escribir el radicando con un exponente igual al índice.

Ejemplo$\PageIndex{7}$:

Simplificar:

1. $\sqrt [ 4 ] { 81 }$
2. $\sqrt [ 5 ] { 32 }$
3. $\sqrt [ 7 ] { 1 }$
4. $\sqrt [ 4 ] { \frac { 1 } { 16 } }$

Solución

1. $\sqrt [ 4 ] { 81 } = \sqrt [ 4 ] { 3 ^ { 4 } } = 3$
2. $\sqrt [ 5 ] { 32 } = \sqrt [ 5 ] { 2 ^ { 5 } } = 2$
3. $\sqrt [ 7 ] { 1 } = \sqrt [ 7 ] { 1 ^ { 7 } } = 1$
4. $\sqrt [ 4 ] { \frac { 1 } { 16 } } = \sqrt [ 4 ] { \left( \frac { 1 } { 2 } \right) ^ { 4 } } = \frac { 1 } { 2 }$

Nota

Si el índice es$n = 2$, entonces el radical indica una raíz cuadrada y se acostumbra escribir el radical sin el índice;$\sqrt [ 2 ] { a } = \sqrt { a }$.

Ya nos hemos ocupado de definir la raíz cuadrada principal de un número real. En este punto, extendemos esta idea a enésima raíces cuando n es parejo. Por ejemplo,$3$ es una cuarta raíz de$81$, porque$3^{4} = 81$. Y ya que$(−3)^{4} = 81$, podemos decir que$−3$ es una cuarta raíz de$81$ también. De ahí que usamos el signo radical$\sqrt [ n ] { }$ para denotar la raíz principal (no negativa)$n$ th ¹⁰ cuando$n$ es par. En este caso, para cualquier número real$a$, utilizamos la siguiente propiedad:

$\sqrt [ n ] { a ^ { n } } = | a | \quad \color{Cerulean} { When\:n\:is\:even }$

Por ejemplo,

$\begin{aligned} \sqrt [ 4 ] { 81 } & = \sqrt [ 4 ] { 3 ^ { 4 } } \quad\quad= |3| \:\:\:\:\:= 3 \\ \sqrt [ 4 ] { 81 } & = \sqrt [ 4 ] { ( - 3 ) ^ { 4 } } \:\:= | - 3 | = 3 \end{aligned}$

La raíz$n$ th negativa, cuando$n$ es par, se denotará usando un signo negativo frente al radical$- \sqrt [ n ] { }$.

$- \sqrt [ 4 ] { 81 } = - \sqrt [ 4 ] { 3 ^ { 4 } } = - 3$

Hemos visto que la raíz cuadrada de un número negativo no es real porque cualquier número real que sea cuadrado dará como resultado un número positivo. De hecho, surge un problema similar para cualquier índice par:

$\sqrt [ 4 ] { - 81 } =\color{Cerulean}{ ?} \quad \color{black}{\text { or }} \quad (\color{Cerulean}{ ?}\color{black}{ )} ^ { 4 } = - 81$

Podemos ver que una cuarta raíz de no$−81$ es un número real porque la cuarta potencia de cualquier número real siempre es positiva.

$\left. \begin{array} { l } { \sqrt { - 4 } } \\ { \sqrt [ 4 ] { - 81 } } \\ { \sqrt [ 6 ] { - 64 } } \end{array} \right\} \quad \color{Cerulean}{These\:radicals\:are\:not\:real\:numbers.}$

Se le anima a probar todos estos en una calculadora. ¿Qué dice?

Ejemplo$\PageIndex{8}$:

Simplificar.

1. $\sqrt [ 4 ] { ( - 10 ) ^ { 4 } }$
2. $\sqrt [ 4 ] { - 10 ^ { 4 } }$
3. $\sqrt [ 6 ] { ( 2 y + 1 ) ^ { 6 } }$

Solución

Dado que los índices son pares, utilice valores absolutos para asegurar resultados no negativos.

1. $\sqrt [ 4 ] { ( - 10 ) ^ { 4 } } = | - 10 | = 10$
2. $\sqrt [ 4 ] { - 10 ^ { 4 } } = \sqrt [ 4 ] { - 10,000 }$no es un número real.
3. $\sqrt [ 6 ] { ( 2 y + 1 ) ^ { 6 } } = | 2 y + 1 |$

Cuando el índice$n$ es impar, no ocurren los mismos problemas. El producto de un número impar de factores positivos es positivo y el producto de un número impar de factores negativos es negativo. De ahí que cuando el índice$n$ es impar, solo hay una raíz$n$ th real para cualquier número real$a$. Y tenemos la siguiente propiedad:

$\sqrt [ n ] { a ^ { n } } = a \quad \color{Cerulean} { When \: n\:is\:odd}$

Ejemplo$\PageIndex{9}$:

Simplificar.

1. $\sqrt [ 5 ] { ( - 10 ) ^ { 5 } }$
2. $\sqrt [ 5 ] { - 32 }$
3. $\sqrt [ 7 ] { ( 2 y + 1 ) ^ { 7 } }$

Solución

Dado que los índices son impares, no se utiliza el valor absoluto.

1. $\sqrt [ 5 ] { ( - 10 ) ^ { 5 } } = - 10$
2. $\sqrt [ 5 ] { - 32 } = \sqrt [ 5 ] { ( - 2 ) ^ { 5 } } = - 2$
3. $\sqrt [ 7 ] { ( 2 y + 1 ) ^ { 7 } } = 2 y + 1$

En resumen, para cualquier número real$a$ tenemos,

$\begin{aligned} \sqrt [ n ] { a^ { n } } & = | a | \color{Cerulean}\:\:\: { When \: n\: is\: even } \\ \sqrt [ n ] {a^ { n } } & = a \quad\: \color{Cerulean} { When \: n\: is\: odd } \end{aligned}$

Cuando$n$ es impar, la raíz$n$ th es positiva o negativa dependiendo del signo del radicando.

$\begin{aligned} \sqrt [ 3 ] { 27 } & = \sqrt [ 3 ] { 3 ^ { 3 } } = 3 \\ \sqrt [ 3 ] { - 27 } & = \sqrt [ 3 ] { ( - 3 ) ^ { 3 } } = - 3 \end{aligned}$

Cuando$n$ es par, la raíz$n$ th es positiva o no real dependiendo del signo del radicando.

$\begin{aligned} \sqrt [ 4 ] { 16 } & = \sqrt [ 4 ] { 2 ^ { 4 } } \quad\:\:= 2 \\ \sqrt [ 4 ] { 16 } & = \sqrt [ 4 ] { ( - 2 ) ^ { 4 } } = | - 2| = 2 \\ \sqrt [ 4 ] { - 16 } & \quad\color{Cerulean} { Not \:a \:real\: number } \end{aligned}$

Ejercicio$\PageIndex{2}$

Simplificar:$- 8 \sqrt [ 5 ] { - 32 }$.

Responder

$16$

www.youtube.com/V/IK1xxGQ18F0

Simplificando los radicales

No siempre va a darse el caso de que el radicando sea una potencia perfecta del índice dado. Si no lo es, entonces usamos la regla del producto para los radicales ¹¹ y la regla del cociente para los radicales ¹² para simplificarlos. Dados los números reales$\sqrt [ n ] { A }$ y$\sqrt [ n ] { B }$,

Mesa$\PageIndex{3}$

Regla del Producto para Radicales:	$\sqrt [ n ] { A \cdot B } = \sqrt [ n ] { A } \cdot \sqrt [ n ] { B }$
Regla de cociente para radicales:	$\sqrt [ n ] { \frac { A } { B } } = \frac { \sqrt [ n ] { A } } { \sqrt [ n ] { B } }$

Un radical se simplifica ¹³ si no contiene ningún factor que pueda escribirse como potencias perfectas del índice.

Ejemplo$\PageIndex{10}$:

Simplificar:$\sqrt { 150 }$.

Solución

Aquí$150$ se puede escribir como$2 \cdot 3 \cdot 5 ^ { 2 }$.

$\begin{aligned} \sqrt { 150 } & = \sqrt { 2 \cdot 3 \cdot 5 ^ { 2 } }\quad\quad \color{Cerulean} { Apply\: the\: product \:rule\: for\: radicals.} \\ & = \sqrt { 2 \cdot 3 } \cdot \sqrt { 5 ^ { 2 } }\quad\: \color{Cerulean} { Simplify. } \\ & = \sqrt { 6 } \cdot 5 \\ & = 5 \sqrt { 6 } \end{aligned}$

Podemos verificar nuestra respuesta en una calculadora:

$\sqrt { 150 } \approx 12.25 \quad\text { and }\quad 5 \sqrt { 6 } \approx 12.25$

Además, cabe señalar que

$12.25 ^ { 2 } \approx 150$

Respuesta:

$5 \sqrt { 6 }$

Nota

$5 \sqrt { 6 }$es la respuesta exacta y$12.25$ es una respuesta aproximada. Presentamos respuestas exactas a menos que se indique lo contrario.

Ejemplo$\PageIndex{11}$:

Simplificar:$\sqrt [ 3 ] { 160 }$.

Solución

Utilice la factorización principal de$160$ para encontrar el factor de cubo perfecto más grande:

$\begin{aligned} 160 & = 2 ^ { 5 } \cdot 5 \\ & = \color{Cerulean}{2 ^ { 3} }\color{black}{ \cdot} 2 ^ { 2 } \cdot 5 \end{aligned}$

Reemplazar el radicando con esta factorización y luego aplicar la regla del producto para los radicales.

$\begin{aligned} \sqrt [ 3 ] { 160 } & = \sqrt [ 3 ] { 2 ^ { 3 } \cdot 2 ^ { 2 } \cdot 5 } \quad\quad\color{Cerulean} { Apply\:the\: product\: rule\: for\: radicals.} \\ & = \sqrt [ 3 ] { 2 ^ { 3 } } \cdot \sqrt [ 3 ] { 2 ^ { 2 } \cdot 5 }\quad \color{Cerulean} { Simplify. } \\ & = 2 \cdot \sqrt [ 3 ] { 20 } \end{aligned}$

Podemos verificar nuestra respuesta en una calculadora.

$\sqrt [ 3 ] { 160 } \approx 5.43 \text { and } 2 \sqrt [ 3 ] { 20 } \approx 5.43$

Respuesta:

$2 \sqrt [ 3 ] { 20 }$

Ejemplo$\PageIndex{12}$:

Simplificar:$\sqrt [ 5 ] { - 320 }$.

Solución

Aquí observamos que el índice es impar y el radicando es negativo; de ahí que el resultado sea negativo. Podemos facturar el radicando de la siguiente manera:

$- 320 = - 1 \cdot 32 \cdot 10 = ( - 1 ) ^ { 5 } \cdot ( 2 ) ^ { 5 } \cdot 10$

Luego simplifique:

$\begin{aligned} \sqrt [ 5 ] { - 320 } & = \sqrt [ 5 ] { ( - 1 ) ^ { 5 } \cdot ( 2 ) ^ { 5 } \cdot 10 } \quad\quad\quad\color{Cerulean} { Apply\: the\: product\: rule\: for\: radicals.} \\ & = \sqrt [ 5 ] { ( - 1 ) ^ { 5 } } \cdot \sqrt [ 5 ] { ( 2 ) ^ { 5 } } \cdot \sqrt [ 5 ] { 10 }\quad \color{Cerulean} { Simplify. } \\ &= -1\cdot2\cdot \sqrt[5]{10} \\ &=-2\cdot \sqrt[5]{10}\end{aligned}$

Respuesta:

$- 2 \sqrt [ 5 ] { 10 }$

Ejemplo$\PageIndex{13}$:

Simplificar:$\sqrt [ 3 ] { - \frac { 8 } { 64 } }$.

Solución

En este caso, considerar la fracción equivalente con$−8 = (−2)^{3}$ en el numerador y$64 = 4^{3}$ en el denominador y luego simplificar.

$\begin{aligned} \sqrt [ 3 ] { - \frac { 8 } { 64 } } & = \sqrt [ 3 ] { \frac { - 8 } { 64 } } \quad\quad\quad\color{Cerulean} { Apply\: the\: quotient \:rule\: for\: radicals.} \\ & = \frac { \sqrt [ 3 ] { ( - 2 ) ^ { 3 } } } { \sqrt [ 3 ] { 4 ^ { 3 } } }\quad\:\:\: \color{Cerulean} { Simplify. } \\ & = \frac { - 2 } { 4 } \\ & = - \frac { 1 } { 2 } \end{aligned}$

Respuesta:

$-\frac{1}{2}$

Ejercicio$\PageIndex{3}$

Simplificar:$\sqrt [ 4 ] { \frac { 80 } { 81 } }$

Responder

$\frac { 2 \sqrt [ 4 ] { 5 } } { 3 }$

www.youtube.com/v/8cwbdbfo2fq

Claves para llevar

• Para simplificar una raíz cuadrada, busque el factor cuadrado perfecto más grande del radicando y luego aplique la regla del producto o cociente para los radicales.
• Para simplificar una raíz cubo, busque el factor cubo perfecto más grande del radicando y luego aplique la regla del producto o cociente para los radicales.
• Al trabajar con enésima raíz,$n$ determina la definición que aplica. Usamos$\sqrt [ n ] { a ^ { n } } = a _ { 1 }$ cuando$n$ es impar y$\sqrt [ n ] { a ^ { n } } = | a |$ cuando$n$ es par.
• Para simplificar$n$ las raíces, busque los factores que tengan un poder que sea igual al índice$n$ y luego aplique la regla del producto o cociente para los radicales. Por lo general, el proceso se simplifica si se trabaja con la factorización principal del radicando.

Ejercicio$\PageIndex{4}$

Simplificar.

1. $\sqrt { 36 }$
2. $\sqrt { 100 }$
3. $\sqrt { \frac { 4 } { 9 } }$
4. $\sqrt { \frac { 1 } { 64 } }$
5. $- \sqrt { 16 }$
6. $- \sqrt { 1 }$
7. $\sqrt { ( - 5 ) ^ { 2 } }$
8. $\sqrt { ( - 1 ) ^ { 2 } }$
9. $\sqrt { - 4 }$
10. $\sqrt { - 5 ^ { 2 } }$
11. $- \sqrt { ( - 3 ) ^ { 2 } }$
12. $- \sqrt { ( - 4 ) ^ { 2 } }$
13. $\sqrt { x ^ { 2 } }$
14. $\sqrt { ( - x ) ^ { 2 } }$
15. $\sqrt { ( x - 5 ) ^ { 2 } }$
16. $\sqrt { ( 2 x - 1 ) ^ { 2 } }$
17. $\sqrt [ 3 ] { 64 }$
18. $\sqrt [ 3 ] { 216 }$
19. $\sqrt [ 3 ] { - 216 }$
20. $\sqrt [ 3 ] { - 64 }$
21. $\sqrt [ 3 ] { - 8 }$
22. $\sqrt [ 3 ] { 1 }$
23. $- \sqrt [ 3 ] { ( - 2 ) ^ { 3 } }$
24. $- \sqrt [ 3 ] { ( - 7 ) ^ { 3 } }$
25. $\sqrt [ 3 ] { \frac { 1 } { 8 } }$
26. $\sqrt [ 3 ] { \frac { 8 } { 27 } }$
27. $\sqrt [ 3 ] { ( - y ) ^ { 3 } }$
28. $- \sqrt [ 3 ] { y ^ { 3 } }$
29. $\sqrt [ 3 ] { ( y - 8 ) ^ { 3 } }$
30. $\sqrt [ 3 ] { ( 2 x - 3 ) ^ { 3 } }$

Responder

1. $6$

3. $\frac{2}{3}$

5. $−4$

7. $5$

9. No es un número real

11. $−3$

13. $|x|$

15. $|x − 5|$

17. $4$

19. $−6$

21. $−2$

23. $2$

25. $\frac{1}{2}$

27. $−y$

29. $y − 8$

Ejercicio$\PageIndex{5}$

Determinar el dominio de la función dada.

1. $g ( x ) = \sqrt { x + 5 }$
2. $g ( x ) = \sqrt { x - 2 }$
3. $f ( x ) = \sqrt { 5 x + 1 }$
4. $f ( x ) = \sqrt { 3 x + 4 }$
5. $g ( x ) = \sqrt { - x + 1 }$
6. $g ( x ) = \sqrt { - x - 3 }$
7. $h ( x ) = \sqrt { 5 - x }$
8. $h ( x ) = \sqrt { 2 - 3 x }$
9. $g ( x ) = \sqrt [ 3 ] { x + 4 }$
10. $g ( x ) = \sqrt [ 3 ] { x - 3 }$

Responder

1. $[ - 5 , \infty )$

3. $\left[ - \frac { 1 } { 5 } , \infty \right)$

5. $( - \infty , 1 ]$

7. $( - \infty , 5 ]$

9. $( - \infty , \infty )$

Ejercicio$\PageIndex{6}$

Evaluar dada la definición de función.

1. Dado$f ( x ) = \sqrt { x - 1 }$, encontrar$f ( 1 ) , f ( 2 )$, y$f ( 5 )$
2. Dado$f ( x ) = \sqrt { x + 5 }$, encontrar$f ( - 5 ) , f ( - 1 )$, y$f ( 20 )$
3. Dado$f ( x ) = \sqrt { x } + 3$, encontrar$f ( 0 ) , f ( 1 )$, y$f(16)$
4. Dado$f ( x ) = \sqrt { x } - 5$, encontrar$f ( 0 ) , f ( 1 )$, y$f(25)$
5. Dado$g ( x ) = \sqrt [ 3 ] { x }$, encontrar$g ( - 1 ) , g ( 0 )$, y$g(1)$
6. Dado$g ( x ) = \sqrt [ 3 ] { x } - 2$ hallazgo$g ( - 1 ) , g ( 0 )$, y$g(8)$
7. Dado$g ( x ) = \sqrt [ 3 ] { x + 7 }$, encontrar$g ( - 15 ) , g ( - 7 )$, y$g(20)$
8. Dado$g ( x ) = \sqrt [ 3 ] { x - 1 } + 2$, encontrar$g ( 0 ) , g ( 2 )$, y$g(9)$

Responder

1. $f ( 1 ) = 0 ; f ( 2 ) = 1 ; f ( 5 ) = 2$

3. $f ( 0 ) = 3 ; f ( 1 ) = 4 ; f ( 16 ) = 7$

5. $g ( - 1 ) = - 1 ; g ( 0 ) = 0 ; g ( 1 ) = 1$

7. $g ( - 15 ) = - 2 ; g ( - 7 ) = 0 ; g ( 20 ) = 3$

Ejercicio$\PageIndex{7}$

Esbozar la gráfica de la función dada y dar su dominio y rango.

1. $f ( x ) = \sqrt { x + 9 }$
2. $f ( x ) = \sqrt { x - 3 }$
3. $f ( x ) = \sqrt { x - 1 } + 2$
4. $f ( x ) = \sqrt { x + 1 } + 3$
5. $g ( x ) = \sqrt [ 3 ] { x - 1 }$
6. $g ( x ) = \sqrt [ 3 ] { x + 1 }$
7. $g ( x ) = \sqrt [ 3 ] { x } - 4$
8. $g ( x ) = \sqrt [ 3 ] { x } + 5$
9. $g ( x ) = \sqrt [ 3 ] { x + 2 } - 1$
10. $g ( x ) = \sqrt [ 3 ] { x - 2 } + 3$
11. $f ( x ) = - \sqrt [ 3 ] { x }$
12. $f ( x ) = - \sqrt [ 3 ] { x - 1 }$

Responder

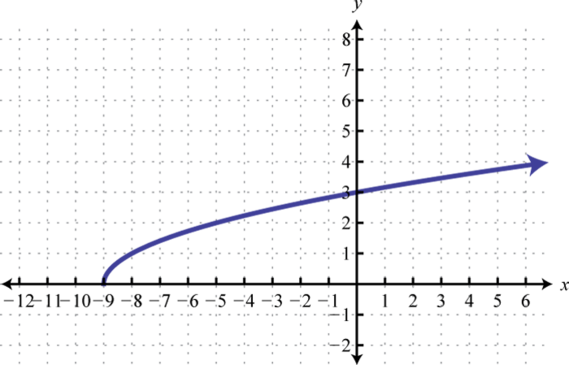
1. Dominio:$[ - 9 , \infty )$; rango:$[ 0 , \infty )$

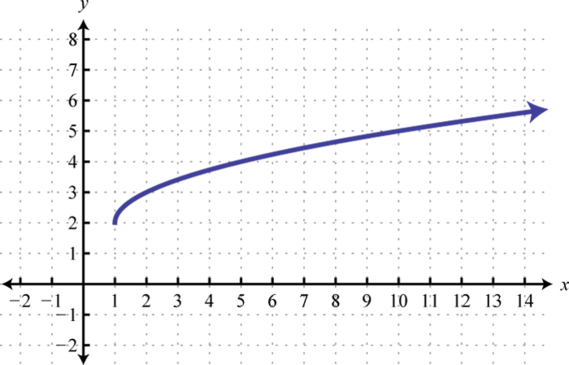
Figura$\PageIndex{4}$

3. Dominio:$[ 1 , \infty )$; rango:$[ 2 , \infty )$

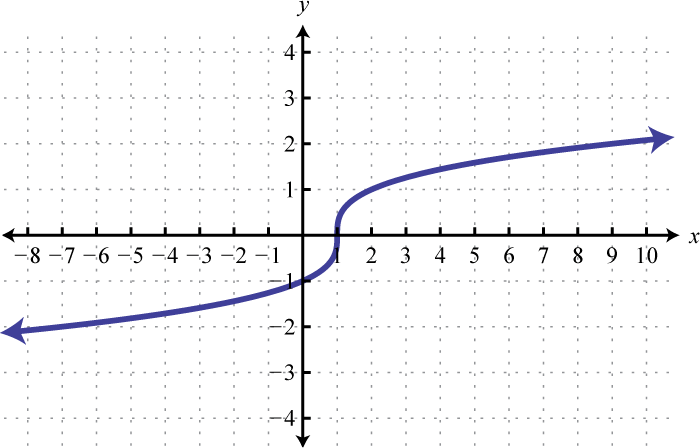
Figura$\PageIndex{5}$

5. Dominio:$\mathbb { R }$; rango;$\mathbb { R }$

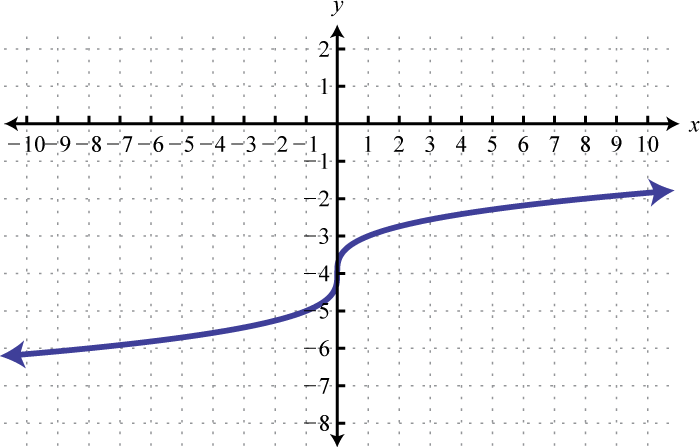
Figura$\PageIndex{6}$

7. Dominio:$\mathbb { R }$; rango;$\mathbb { R }$

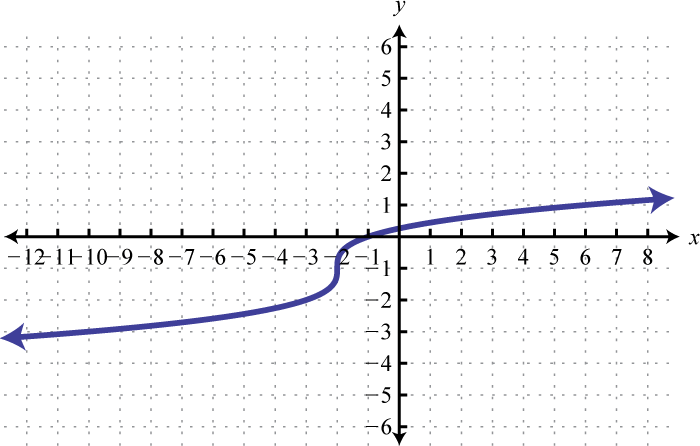
Figura$\PageIndex{7}$

9. Dominio:$\mathbb { R }$; rango;$\mathbb { R }$

Figura$\PageIndex{8}$

11. Dominio:$\mathbb { R }$; rango;$\mathbb { R }$

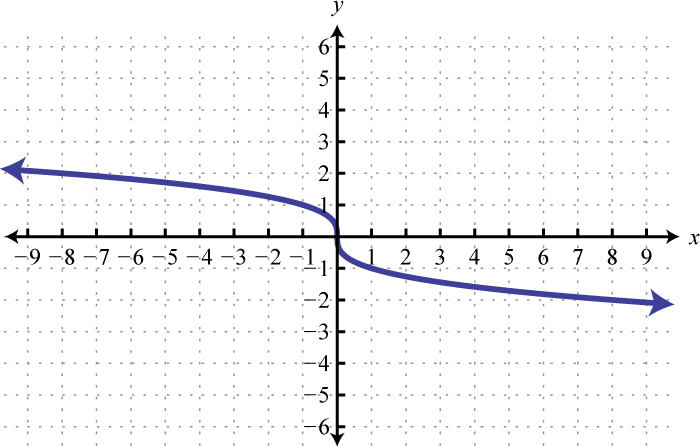
Figura$\PageIndex{9}$

Ejercicio$\PageIndex{8}$

Simplificar.

1. $\sqrt [ 4 ] { 64 }$
2. $\sqrt [ 4 ] { 16 }$
3. $\sqrt [ 4 ] { 625 }$
4. $\sqrt [ 4 ] { 1 }$
5. $\sqrt [ 4 ] { 256 }$
6. $\sqrt [ 4 ] { 10,000 }$
7. $\sqrt [ 5 ] { 243 }$
8. $\sqrt [ 5 ] { 100,000 }$
9. $\sqrt [ 5 ] { \frac { 1 } { 32 } }$
10. $\sqrt [ 5 ] { \frac { 1 } { 243 } }$
11. $- \sqrt [ 4 ] { 16 }$
12. $- \sqrt [ 6 ] { 1 }$
13. $\sqrt [ 5 ] { - 32 }$
14. $\sqrt [ 5 ] { - 1 }$
15. $\sqrt { - 1 }$
16. $\sqrt [ 4 ] { - 16 }$
17. $- 6 \sqrt [ 3 ] { - 27 }$
18. $- 5 \sqrt [ 3 ] { - 8 }$
19. $2 \sqrt [ 3 ] { - 1,000 }$
20. $7 \sqrt [ 5 ] { - 243 }$
21. $6 \sqrt [ 4 ] { - 16 }$
22. $12 \sqrt [ 6 ] { - 64 }$
23. $\sqrt [ 3 ] { \frac { 25 } { 16 } }$
24. $6 \sqrt { \frac { 16 } { 9 } }$
25. $5 \sqrt [ 3 ] { \frac { 27 } { 125 } }$
26. $7 \sqrt [ 5 ] { \frac { 32 } { 7 ^ { 5 } } }$
27. $- 5 \sqrt [ 3 ] { \frac { 8 } { 27 } }$
28. $- 8 \sqrt [ 4 ] { \frac { 625 } { 16 } }$
29. $2 \sqrt [ 5 ] { 100,000 }$
30. $2 \sqrt [ 7 ] { 128 }$

Responder

1. $4$

3. $5$

5. $4$

7. $3$

9. $\frac{1}{2}$

11. $−2$

13. $−2$

15. No es un número real

17. $18$

19. $−20$

21. No es un número real

23. $\frac{15}{4}$

25. $3$

27. $−\frac{10}{3}$

29. $20$

Ejercicio$\PageIndex{9}$

Simplificar.

1. $\sqrt { 96 }$
2. $\sqrt { 500 }$
3. $\sqrt { 480 }$
4. $\sqrt { 450 }$
5. $\sqrt { 320 }$
6. $\sqrt { 216 }$
7. $5 \sqrt { 112 }$
8. $10 \sqrt { 135 }$
9. $- 2 \sqrt { 240 }$
10. $- 3 \sqrt { 162 }$
11. $\sqrt { \frac { 150 } { 49 } }$
12. $\sqrt { \frac { 200 } { 9 } }$
13. $\sqrt { \frac { 675 } { 121 } }$
14. $\sqrt { \frac { 192 } { 81 } }$
15. $\sqrt [ 3 ] { 54 }$
16. $\sqrt [ 3 ] { 24 }$
17. $\sqrt [ 3 ] { 48 }$
18. $\sqrt [ 3 ] { 81 }$
19. $\sqrt [ 3 ] { 40 }$
20. $\sqrt [ 3 ] { 120 }$
21. $\sqrt [ 3 ] { 162 }$
22. $\sqrt [ 3 ] { 500 }$
23. $\sqrt [ 3 ] { \frac { 54 } { 125 } }$
24. $\sqrt [ 3 ] { \frac { 40 } { 343 } }$
25. $5 \sqrt [ 3 ] { - 48 }$
26. $2 \sqrt [ 3 ] { - 108 }$
27. $8 \sqrt [ 4 ] { 96 }$
28. $7 \sqrt [ 4 ] { 162 }$
29. $\sqrt [ 5 ] { 160 }$
30. $\sqrt [ 5 ] { 486 }$
31. $\sqrt [ 5 ] { \frac { 224 } { 243 } }$
32. $\sqrt [ 5 ] { \frac { 5 } { 32 } }$
33. $\sqrt [ 5 ] { - \frac { 1 } { 32 } }$
34. $\sqrt [ 6 ] { - \frac { 1 } { 64 } }$

Responder

1. $4 \sqrt { 6 }$

3. $4 \sqrt { 30 }$

5. $8 \sqrt { 5 }$

7. $20 \sqrt { 7 }$

9. $- 8 \sqrt { 15 }$

11. $\frac { 5 \sqrt { 6 } } { 7 }$

13. $\frac { 15 \sqrt { 3 } } { 11 }$

15. $3 \sqrt [ 3 ] { 2 }$

17. $2 \sqrt [ 3 ] { 6 }$

19. $2 \sqrt [ 3 ] { 5 }$

21. $3 \sqrt [ 3 ] { 6 }$

23. $\frac { 3 \sqrt [ 3 ] { 2 } } { 5 }$

25. $- 10 \sqrt [ 3 ] { 6 }$

27. $16 \sqrt [ 4 ] { 6 }$

29. $2 \sqrt [ 5 ] { 5 }$

31. $\frac { 2 \sqrt [ 5 ] { 7 } } { 3 }$

33. $- \frac { 1 } { 2 }$

Ejercicio$\PageIndex{10}$

Simplificar. Dar la respuesta exacta y la respuesta aproximada redondeada a la centésima más cercana.

1. $\sqrt { 60 }$
2. $\sqrt { 600 }$
3. $\sqrt { \frac { 96 } { 49 } }$
4. $\sqrt { \frac { 192 } { 25 } }$
5. $\sqrt [ 3 ] { 240 }$
6. $\sqrt [ 3 ] { 320 }$
7. $\sqrt [ 3 ] { \frac { 288 } { 125 } }$
8. $\sqrt [ 3 ] { \frac { 625 } { 8 } }$
9. $\sqrt [ 4 ] { 486 }$
10. $\sqrt [ 5 ] { 288 }$

Responder

1. $2 \sqrt { 15 } ; 7.75$

3. $\frac { 4 \sqrt { 6 } } { 7 } ; 1.40$

5. $2 \sqrt [ 3 ] { 30 } ; 6.21$

7. $\frac { 2 \sqrt [ 3 ] { 36 } } { 5 } ; 1.32$

9. $3 \sqrt [ 4 ] { 6 } ; 4.70$

Ejercicio$\PageIndex{11}$

Reescribir lo siguiente como una expresión radical con coeffecient$1$.

1. $2 \sqrt { 15 }$
2. $3 \sqrt { 7 }$
3. $5 \sqrt { 10 }$
4. $10 \sqrt { 3 }$
5. $2 \sqrt [ 3 ] { 7 }$
6. $3 \sqrt [ 3 ] { 6 }$
7. $2 \sqrt [ 4 ] { 5 }$
8. $3\sqrt [ 4 ] { 2 }$
9. Cada lado de un cuadrado tiene una longitud que es igual a la raíz cuadrada del área del cuadrado. Si el área de un cuadrado es unidades$72$ cuadradas, encuentra la longitud de cada uno de sus lados.
10. Cada borde de un cubo tiene una longitud que es igual a la raíz cúbica del volumen del cubo. Si el volumen de un cubo es de unidades$375$ cúbicas, encuentra la longitud de cada uno de sus bordes.
11. La corriente$I$ medida en amperios viene dada por la fórmula$I = \sqrt { \frac { P } { R } }$ donde$P$ se mide el consumo de energía en vatios y$R$ es la resistencia medida en ohmios. Si una bombilla de$100$ vatio tiene$160$ ohmios de resistencia, encuentre la corriente necesaria. (Redondear a la centésima más cercana de un amperio.)
12. El tiempo en segundos que un objeto está en caída libre viene dado por la fórmula$t = \frac { \sqrt { s } } { 4 }$ donde$s$ representa la distancia en pies que ha caído el objeto. ¿Cuánto tiempo tardará un objeto en caer al suelo desde lo alto$8$ de una escalera de mano? (Redondear a la décima de segundo más cercana.)

Responder

1. $\sqrt { 60 }$

3. $\sqrt { 250 }$

5. $\sqrt [ 3 ] { 56 }$

7. $\sqrt [ 4 ] { 80 }$

9. $6 \sqrt { 2 }$unidades

11. $0.79$amperio

Ejercicio$\PageIndex{12}$

1. Explica por qué hay dos raíces cuadradas reales para cualquier número real positivo y una raíz cubo real para cualquier número real.
2. ¿De qué es la raíz cuadrada$1$ y de qué es la raíz cúbica$1$? Explique por qué.
3. $\sqrt { - 1 }$Explique por qué no es un número real y por qué$\sqrt [ 3 ] { - 1 }$ es un número real.
4. Investigar y discutir los métodos utilizados para calcular raíces cuadradas antes del uso común de las calculadoras electrónicas.

Responder

1. La respuesta puede variar

3. La respuesta puede variar

Notas al pie

¹ Un número que al multiplicarse por sí mismo produce el número original.

² La raíz cuadrada positiva de un número real positivo, denotada con el símbolo$√$.

³ La expresión$A$ dentro de un signo radical,$\sqrt [ n ] { A }$.

⁴ La función definida por$f ( x ) = \sqrt { x }$.

⁵ Un número que cuando se usa como factor consigo mismo tres veces produce el número original, denotado con el símbolo$\sqrt [ 3 ] { }$.

⁶ El entero positivo$n$ en la notación$\sqrt [ n ] { }$ que se utiliza para indicar una raíz enésima.

⁷ La función definida por$f ( x ) = \sqrt [ 3 ] { x }$.

⁸ Un número que cuando se eleva a la potencia$n$ th$(n ≥ 2)$ produce el número original.

⁹ Se utiliza cuando se refiere a una expresión de la forma$\sqrt [ n ] { A }$.

¹⁰ La raíz$n$ th positiva cuando$n$ es par.

¹¹ Dados los números reales$\sqrt [ n ] { A }$ y$\sqrt [ n ] { B }$,$\sqrt [ n ] { A \cdot B } = \sqrt [ n ] { A } \cdot \sqrt [ n ] { B }$.

¹² Dados números reales$\sqrt [ n ] { A }$ y$\sqrt [ n ] { B }$,$\sqrt [ n ] { \frac { A } { B } } = \frac { \sqrt [ n ] { A } } { \sqrt [ n ] { B } }$ dónde$B ≠ 0$.

¹³ Un radical donde el radicando no consiste en ningún factor que pueda escribirse como poderes perfectos del índice.