7.4: Resolver ecuaciones racionales

Última actualización
Guardar como PDF

Page ID: 111645

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

En la Sección 3 del Capítulo 2, demostramos que la forma más eficiente de resolver una ecuación que contenía fracciones era limpiar primero las fracciones multiplicando ambos lados de la ecuación por el mínimo denominador común. Por ejemplo, dada la ecuación

\[\dfrac{1}{2}x+\dfrac{1}{3}=\dfrac{1}{4} \nonumber \]

primero limpiaríamos las fracciones multiplicando ambos lados por$12$.

\[\begin{align*} 12\left [ \dfrac{1}{2}x + \dfrac{1}{3}\right ] &= \left [ \dfrac{1}{4} \right ]12\\ 6x+4 &= 3 \end{align*} \nonumber \]

Este procedimiento funciona igualmente bien cuando los denominadores contienen una variable.

Ejemplo$\PageIndex{1}$

Resolver para$x$:$1-\dfrac{2}{x} = \dfrac{3}{x^2}$

Solución

El denominador común es$x^2$. Comenzamos limpiando fracciones, multiplicando ambos lados de la ecuación por$x^2$.

\[\begin{align*} 1-\dfrac{2}{x} &= \dfrac{3}{x^2} \quad \color {Red} \text {Original equation.}\\ {\color {Red} x^2}\left [1- \dfrac{2}{x} \right] &= \left [ \dfrac{3}{x^2} \right ]{\color {Red} x^2} \quad \color {Red} \text {Multiply both sides by } x^2. \end{align*} \nonumber \]

Ahora usamos la propiedad distributiva.

\[{\color {Red} x^2}[1]-{\color {Red} x^2}\left [\dfrac{2}{x} \right ] = \left [\dfrac{3}{x^2} \right ]{\color {Red} x^2} \quad \color {Red} \text {Distribute } x^2. \nonumber \]

Ahora cancelamos factores comunes y simplificamos.

\[x^2 - 2x =3 \quad \color {Red} \text {Cancel. Simplify. } \nonumber \]

La ecuación resultante es no lineal ($x$se eleva a una potencia mayor que$1$). Hacer un lado cero, luego factorial.

\[\begin{align*} x^2-2x-3 &= 0 \quad \color {Red} \text {Nonlinear. Make one side zero.}\\ (x-3)(x+1) &= 0 \quad \color {Red} \text {Factor.} \end{align*} \nonumber \]

Utilice la propiedad cero del producto para completar la solución. O el primer factor es cero o el segundo factor es cero.

\[\begin{align*} x-3 &= 0 \\ x &= 3 \end{align*} \nonumber\]

\[\begin{align*} x+1 &= 0 \\ x &= -1 \end{align*} \nonumber\]

De ahí que las soluciones sean$x = −1$ y$x = 3$.

Cheque. Sustituir$−1$$x$, luego$3$ por$x$ en la ecuación original y simplificar.

\[\begin{align*} 1-\dfrac{2}{x} &= \dfrac{3}{x^2} \\ 1-\dfrac{2}{({\color {Red} -1})^2} &= \dfrac{3}{({\color {Red} -1})^2} \\ 1+2 &= 3\\ 3 &= 3 \end{align*} \nonumber\]

\[\begin{align*} 1-\dfrac{2}{x} &= \dfrac{3}{x^2} \\ 1-\dfrac{2}{({\color {Red} 3})} &= \dfrac{3}{({\color {Red} 3})^2} \\ 1-\dfrac{2}{3} &= \dfrac{3}{9}\\ \dfrac{1}{3} &= \dfrac{1}{3} \end{align*} \nonumber\]

Tenga en cuenta que ambos resultan en declaraciones verdaderas, lo que demuestra que ambos$x =−1$ y$x =3$ verifican la ecuación original.

Ejercicio$\PageIndex{1}$

Resolver para$x$:$1-\dfrac{6}{x} = -\dfrac{8}{x^2}$

Contestar: $2,4$

Ejemplo$\PageIndex{2}$

Resolver para$x$:$6-\dfrac{22}{x^2}=\dfrac{29}{x}$

Solución

El denominador común es$x^2$.

\[\begin{align*} 6-\dfrac{22}{x^2} &= \dfrac{29}{x} \quad \color {Red} \text {Original equation.}\\ {\color {Red} x^2}\left [6-\dfrac{22}{x^2} \right ] &= \left [\dfrac{29}{x} \right ] {\color {Red} x^2} \quad \color {Red} \text {Multiply both sides by } x^2\\ {\color {Red} x^2}[6]-{\color {Red} x^2}\left [\dfrac{22}{x^2} \right ] &= \left [\dfrac{29}{x} \right ] {\color {Red} x^2} \quad \color {Red} \text {Distribute } x^2 \\ 6x^2-22 &= 29x \quad \color {Red} \text {Cancel and Simplify.} \end{align*} \nonumber \]

Esta última ecuación es no lineal. Hacer un lado cero.

\[6x^2 −29x−22 = 0 \nonumber \]

El par entero$4$ y$−33$ tiene producto$ac = −132$ y suma$b = −29$. Divida el término medio en una suma usando este par, luego factorizar por agrupación.

\[\begin{align*} 6x^2 +4x-33x-22 &= 0 \\ 2x(3x + 2)-11(3x + 2) &= 0 \\ (2x - 11)(3x + 2) &= 0 \end{align*} \nonumber \]

Por último, utilice la propiedad cero del producto para escribir:

\[\begin{align*} 2x - 11 &= 0 \\ 2x &= 11 \\ x &= \dfrac{11}{2} \end{align*} \nonumber \]

\[\begin{align*} 3x + 2 &= 0 \\ 3x &= -2 \\ x &= -\dfrac{2}{3} \end{align*}\]

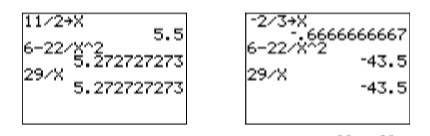
Consulta: Comprobemos estas soluciones con nuestras calculadoras. Ingrese$11/2$, presione el botón STO►, presione el$\mathrm{X,T,\theta,n}$ botón y la tecla ENTER (vea la pantalla de la calculadora a la izquierda en la Figura$\PageIndex{1}$). A continuación, ingrese el lado izquierdo de la ecuación como$6-22/X^2$ y presione ENTRAR. Ingrese el lado derecho de la ecuación como$29/X$ y presione ENTRAR. Los resultados son los mismos (ver la pantalla de la calculadora a la izquierda en la Figura$\PageIndex{1}$). Esto verifica que$11/2$ sea una solución de$6−22/x^2 = 29/x$.

La pantalla de la calculadora a la derecha en la Figura$\PageIndex{1}$ muestra una comprobación similar de la solución$x = −2/3$.

higo 7.4.1.png — Figura$\PageIndex{1}$: Comprobando las soluciones de$6-\dfrac{22}{x^2}=\dfrac{29}{x}$

Ejercicio$\PageIndex{2}$

Resolver para$x$:$\dfrac{7}{x^2}+8=-\dfrac{30}{x}$

Contestar: $−1/4, −7/2$

Resolver ecuaciones racionales con la calculadora gráfica

Usemos la calculadora gráfica para resolver una ecuación que contenga expresiones racionales.

Ejemplo$\PageIndex{3}$

Considera la siguiente ecuación:\[2-\dfrac{9}{x}=\dfrac{5}{x^2} \nonumber \] Resuelve la ecuación algebraicamente, luego resuelve la ecuación gráficamente usando tu calculadora gráfica. Compara tus soluciones.

Solución

Solución algebraica: Primero, un enfoque algebraico. Multiplique ambos lados de la ecuación por el denominador común$x^2$.

\[\begin{align*} 2-\dfrac{9}{x} &= \dfrac{5}{x^2} \quad \color {Red} \text {Original equation.}\\ {\color {Red} x^2}\left [2-\dfrac{9}{x} \right ] &= \left [\dfrac{5}{x^2} \right ] {\color {Red} x^2} \quad \color {Red} \text {Multiply both sides by } x^2\\ {\color {Red} x^2}[2]-{\color {Red} x^2}\left [\dfrac{9}{x} \right ] &= \left [\dfrac{5}{x^2} \right ] {\color {Red} x^2} \quad \color {Red} \text {Distribute } x^2 \\ 2x^2-9x &= 5 \quad \color {Red} \text {Cancel and Simplify.} \end{align*} \nonumber\]

La última ecuación es no lineal. Hacer un lado cero.

\[2x^2 −9x−5=0 \quad \color {Red} \text {Make one side zero.} \nonumber \]

El par entero$−10$ y$1$ tienen igualación de producto$ac = −10$ y suma igual$b = −9$. Romper el término medio usando este par, luego factorizar por agrupación.

\[\begin{align*} 2x^2-10x+x-5 &= 0 \quad \color {Red} -10x+x=-9x\\ 2x(x-5) + 1(x-5) &= 0 \quad \color {Red} \text {Factor by grouping.} \\ (2x + 1)(x-5) &= 0 \quad \color {Red} \text {Factor out } x-5 \end{align*} \nonumber\]

Ahora use la propiedad cero del producto para escribir:

\[\begin{align*} 2x+1 &= 0\\ 2x &= -1\\ x &= -\dfrac{1}{2} \end{align*} \nonumber \]

\[\begin{align*} x-5 &= 0\\ x &= 5 \end{align*} \nonumber\]

De ahí que las soluciones sean$x = −1/2$ y$x = 5$.

Solución gráfica: Podríamos cargar cada lado de la ecuación por separado, luego usar la utilidad intersectar para averiguar dónde se cruzan las gráficas. Sin embargo, en este caso, es un poco más fácil hacer un lado de la ecuación cero, dibujar una sola gráfica, luego anotar dónde la gráfica cruza el$x$ eje -eje.

\[\begin{align*} 2-\dfrac{9}{x} &= \dfrac{5}{x^2} \quad \color {Red} \text {Original equation.} \\ 2-\dfrac{9}{x} - \dfrac{5}{x^2} &= 0 \quad \color {Red} \text {Make one side zero.} \nonumber \end{align*} \nonumber\]

Cargue el lado izquierdo de la ecuación en$\mathrm{Y1}$ as$\mathrm{2-9/X-5/X}\land 2$ (vea la imagen de la izquierda en la Figura$\PageIndex{2}$), luego seleccione 6:ZStandard en el menú ZOOM para producir la imagen a la derecha en la Figura$\PageIndex{2}$.

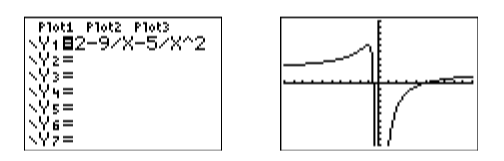
higo 7.4.2.png — Figura$\PageIndex{2}$: Esbozar la gráfica de$y=2-\dfrac{9}{x}-\dfrac{5}{x^2}$.

A continuación, las soluciones de

\[2-\dfrac{9}{x}-\dfrac{5}{x^2} = 0 \nonumber \]

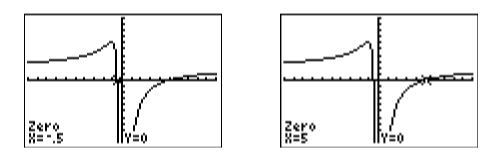
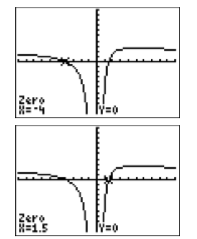
se encuentran señalando donde la gráfica de$y=2-\dfrac{9}{x}-\dfrac{5}{x^2}$ cruzar el$x$ eje. Seleccione 2:cero en el menú CALC. Use las teclas de flecha para mover el cursor a la izquierda de la primera$x$ intercepción, luego presione ENTRAR para establecer el “Límite izquierdo”. A continuación, mueva el cursor a la derecha de la primera$x$ intersección, luego presione ENTRAR para establecer el “Límite a la derecha”. Por último, deja el cursor donde está y presiona ENTRAR para establecer tu “Guess”. La calculadora responde con el resultado mostrado en la ﬁgura de la izquierda en la Figura$\PageIndex{3}$.

Repita el procedimiento de cero-ﬁnding para capturar las coordenadas de la segunda$x$ intersección (vea la imagen de la derecha en la Figura$\PageIndex{3}$).

higo 7.4.3.png — Figura$\PageIndex{3}$: Localización de los ceros de$y=2-\dfrac{9}{x}-\dfrac{5}{x^2}$.

Reportando la solución en tu tarea: Duplica la imagen en la ventana de visualización de tu calculadora en tu página de tareas. Usa una regla para dibujar todas las líneas, pero a mano alzada cualquier curva.

Etiquete los ejes horizontal y vertical con$x$ y$y$, respectivamente (ver Figura$\PageIndex{4}$).
Coloca tus parámetros WINDOW al final de cada eje (ver Figura$\PageIndex{4}$).
Etiquete la gráfica con su ecuación (ver Figura$\PageIndex{4}$).
Deja caer líneas verticales discontinuas a través$x$ de cada intercepción. Sombra y etiquete los$x$ valores -de los puntos donde la línea vertical discontinua cruza el$x$ eje -eje. Estas son las soluciones de la ecuación$2− 9/x− 5/x^2 = 0$ (ver Figura$\PageIndex{4}$).

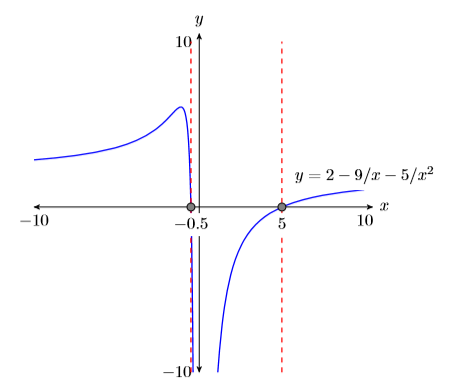
higo 7.4.4.png — Figura$\PageIndex{4}$: Reportando tu solución gráfica en tu tarea.

Así, la calculadora está reportando que las soluciones de$2−9/x −5/x^2 = 0$ son$x =−0.5$ y$x = 5$, que coinciden con las soluciones algebraicas$x = −1/2$ y$x = 5$.

Ejercicio$\PageIndex{3}$

Resuelve la ecuación$2+\dfrac{5}{x}=\dfrac{12}{x^2}$ tanto algebraica como gráficamente, luego compara tus soluciones.

Contestar

$−4, 3/2$

$Ex 7.4.3.png$

Aplicaciones numéricas

Apliquemos lo que hemos aprendido a una aplicación.

Ejemplo$\PageIndex{4}$

La suma de un número y su recíproco es$41/20$. Encuentra el número.

Solución

En la solución, abordamos cada paso de los Requisitos para Soluciones de Problemas de Word.

Configurar un diccionario de variables: Let$x$ representar el número desconocido.
Establecer una ecuación: Si el número desconocido es$x$, entonces su recíproco es$1/x$. Así, la “suma de un número y su recíproco es$41/20$” se convierte en:\[x+\dfrac{1}{x}=\dfrac{41}{20} \nonumber \]
Resuelve la ecuación: Despeja las fracciones multiplicando ambos lados por$20x$, el mínimo denominador común. \[\begin{align*} x+\dfrac{1}{x} &= \dfrac{41}{20} \quad \color {Red} \text {Model equation.}\\ {\color {Red}20x}\left [x+\dfrac{1}{x} \right ] &= \left [\dfrac{41}{20} \right ]{\color {Red}20x} \quad \color {Red} \text {Multiply both sides by }20x\\ {\color {Red}20x}[x]+{\color {Red}20x}\left [\dfrac{1}{x} \right ] &= \left [\dfrac{41}{20} \right ]{\color {Red}20x} \quad \color {Red} \text {Distribute }20x.\\ 20x^2+20 &= 41x \quad \color {Red} \text {Cancel and simplify.} \end{align*} \nonumber \]La ecuación es no lineal. Hacer un lado cero. \[20x^2 −41x + 20 = 0 \quad \color {Red} \text {Make one side zero.}\nonumber \]El par entero$−16$ y$−25$ tiene producto$ac = 400$ y suma$b = −41$. Divida el término medio en la última ecuación en una suma de términos similares usando este par, luego factorizar por agrupación. \[\begin{align*} 20x^2 - 16x-25x + 20 &= 0 \quad \color {Red} -16x-25x=-41x\\ 4x(5x-4)-5(5x-4) &= 0 \quad \color {Red} \text {Factor by grouping.}\\ (4x-5)(5x-4) &= 0 \quad \color {Red} \text {Factor out }5x-4.\\ \end{align*} \nonumber \]Ahora podemos usar la propiedad cero producto para escribir:\[\begin{align*} 4x-5 &= 0 \\ 4x &= 5 \\ x &= \dfrac{5}{4} \end{align*} \nonumber\] o\[\begin{align*} 5x-4 &= 0 \\ 5x &= 4 \\ x &= \dfrac{4}{5} \end{align*} \nonumber\]
Responde a la pregunta: Hay dos números posibles,$5/4$ y$4/5$.
Mirar atrás: Se supone que la suma del número desconocido y su recíproco es igual$41/20$. La respuesta$5/4$ tiene reciprocidad$4/5$. Su suma es:\[\begin{align*} \dfrac{5}{4} + \dfrac{4}{5} &= \dfrac{16}{20} + \dfrac{25}{20}\\ &= \dfrac{41}{20} \end{align*} \nonumber\] Así,$5/4$ es una solución válida. La segunda respuesta$4/5$ tiene reciprocidad$5/4$, por lo que es claro que su suma también lo es$41/20$. De ahí$4/5$ que también sea una solución válida.

Ejercicio$\PageIndex{4}$

La suma de un número y su recíproco es$53/14$. Encuentra el número.

Contestar: $2/7, 7/2$

Search

Text Color

Text Size

Margin Size

Font Type