8.3: Completando la Plaza

Última actualización
Guardar como PDF

Page ID: 111662

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

En Introducción a la notación radical, mostramos cómo resolver ecuaciones tales como$x^2 = 9$ tanto algebraica como gráficamente.

\[\begin{aligned} x^{2} &=9 \\ x &=\pm 3 \end{aligned} \nonumber \]

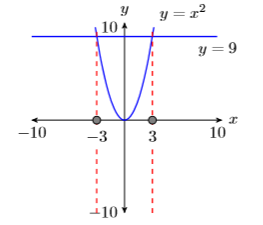
Tenga en cuenta que cuando tomamos la raíz cuadrada de ambos lados de esta ecuación, hay dos respuestas, una negativa y otra positiva.

Un cuadrado perfecto es bonito, pero no requerido. De hecho, es posible que incluso tengamos que factorizar un cuadrado perfecto para poner nuestra respuesta final en forma simple.

\[\begin{aligned} x^{2} &=8 \\ x &=\pm \sqrt{8} \\ x &=\pm \sqrt{4} \sqrt{2} \\ x &=\pm 2 \sqrt{2} \end{aligned} \nonumber \]

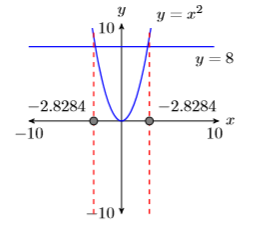
Los lectores deben usar sus calculadoras para verificar eso$-2 \sqrt{2} \approx -2.8284$ y$2 \sqrt{2} \approx 2.8284$.

Ahora, vamos a extender esta técnica de solución a una clase más amplia de ecuaciones.

Ejemplo$\PageIndex{1}$

Resolver para$x : (x-4)^{2}=9$

Solución

Al igual que las soluciones de$x^2 = 9$ son$x = ±3$, utilizamos un enfoque similar$(x−4)^2 = 9$ para obtener:

\[\begin{array}{rlrl}{(x-4)^{2}} & {=9} & {} & \color {Red} {\text { Original equation. }} \\ {x-4} & {=\pm 3} & {} & \color {Red} {\text { There are two square roots. }}\end{array} \nonumber \]

Para completar la solución, agregue$4$ a ambos lados de la ecuación.

\[x=4 \pm 3 \quad \color {Red} \text { Add } 3 \text { to both sides. } \nonumber \]

Tenga en cuenta que esto significa que hay dos respuestas, a saber:

\[\begin{array}{l}{x=4-3} \\ {x=1}\end{array} \nonumber \]

\[\begin{array}{l}{x=4+3} \\ {x=7}\end{array} \nonumber \]

Comprobar: Verifique cada solución sustituyéndola en la ecuación original.

Sustituto$1$ de$x$:

\[\begin{aligned}(x-4)^{2} &=9 \\(1-4)^{2} &=9 \\(-3)^{2} &=9 \end{aligned} \nonumber \]

Sustituto$7$ de$x$:

\[\begin{aligned}(x-4)^{2} &=9 \\(7-4)^{2} &=9 \\(3)^{2} &=9 \end{aligned} \nonumber \]

Debido a que la última declaración en cada cheque es una declaración verdadera, ambas$x = 1$ y$x = 7$ son soluciones válidas de$(x−4)^2 = 9$.

Ejercicio$\PageIndex{1}$

Resolver para$x :(x+6)^{2}=10$

Contestar: $-2$,$-10$

En Ejemplo$\PageIndex{1}$, el lado derecho de la ecuación$(x−4)^2 = 9$ era un cuadrado perfecto. Sin embargo, esto no es obligatorio, como mostrará el siguiente ejemplo.

Ejemplo$\PageIndex{2}$

Resolver para$x :(x+5)^{2}=7$

Solución

Usando la misma técnica que en Ejemplo$\PageIndex{1}$, obtenemos:

\[\begin{array}{rlrl}{(x+5)^{2}} & {=7} & {} & \color {Red} {\text { Original equation. }} \\ {x+5} & {=\pm \sqrt{7}} & {} & \color {Red} {\text { There are two square roots. }}\end{array} \nonumber \]

Para completar la solución, restar 5 de ambos lados de la ecuación.

\[x=-5 \pm \sqrt{7} \quad \color {Red} \text { Subtract } 5 \text { from both sides.} \nonumber \]

Tenga en cuenta que esto significa que hay dos respuestas, a saber:

\[x=-5-\sqrt{7} \quad \text { or } \quad x=-5+\sqrt{7} \nonumber \]

Comprobar: Verifique cada solución sustituyéndola en la ecuación original.

Sustituto$-5-\sqrt{7}$ de$x$:

\[\begin{aligned}(x+5)^{2} &=7 \\((-5-\sqrt{7})+5)^{2} &=7 \\(-\sqrt{7})^{2} &=7 \end{aligned} \nonumber \]

Sustituto$-5+\sqrt{7}$ de$x$:

\[\begin{aligned}(x+5)^{2} &=7 \\((-5+\sqrt{7})+5)^{2} &=7 \\(\sqrt{7})^{2} &=7 \end{aligned} \nonumber \]

Debido a que la última declaración en cada cheque es una declaración verdadera, ambas$x=-5-\sqrt{7}$ y$x=-5+\sqrt{7}$ son soluciones válidas de$(x+5)^{2}=7$.

Ejercicio$\PageIndex{2}$

Resolver para$x :(x-4)^{2}=5$

Contestar: $4+\sqrt{5}, 4-\sqrt{5}$

A veces tendrás que factorizar un cuadrado perfecto para poner tu respuesta en forma sencilla.

Ejemplo$\PageIndex{3}$

Resolver para$x :(x+4)^{2}=20$

Solución

Usando la misma técnica que en Ejemplo$\PageIndex{1}$, obtenemos:

\[\begin{array}{rlrl}{(x+4)^{2}} & {=20} & {} & \color {Red} {\text { Original equation. }} \\ {x+4} & {=\pm \sqrt{20}} & {} & \color {Red} {\text { There are two square roots. }} \\ {x+4} & {=\pm \sqrt{4} \sqrt{5}} & {} & \color {Red} {\text { Factor out a perfect square. }} \\ {x+4} & {=\pm 2 \sqrt{5}} & {} & \color {Red} {\text { Simplify: } \sqrt{4}=2}\end{array} \nonumber \]

Para completar la solución, restar$4$ de ambos lados de la ecuación.

\[x=-4 \pm 2 \sqrt{5} \quad \color {Red} \text { Subtract } 4 \text { from both sides. } \nonumber \]

Tenga en cuenta que esto significa que hay dos respuestas, a saber:

\[x=-4-2 \sqrt{5} \quad \text { or } \quad x=-4+2 \sqrt{5} \nonumber \]

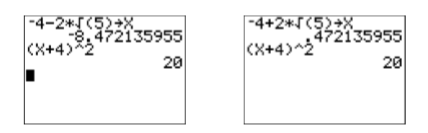
Consulta: Aunque es posible verificar las respuestas exactas, usemos nuestra calculadora en su lugar. Primero, almacene$-4-2 \sqrt{5}$ en$\mathbf{X}$. A continuación, ingrese el lado izquierdo de la ecuación$(x + 4)^2 = 20$ (vea la imagen a la izquierda en la Figura$\PageIndex{3}$). Tenga en cuenta que (x+4) 2 simplifica a 20, mostrando que$-4-2 \sqrt{5}$ es una solución de$(x+4)^2 = 20$.

De manera similar, la solución$-4+2 \sqrt{5}$ también se registra$(x + 4)^2 = 20$ (ver imagen a la derecha en la Figura$\PageIndex{3}$).

higo 8.3.3.png — Figura$\PageIndex{3}$: Comprobación$-4-2 \sqrt{5}$ y$-4+2 \sqrt{5}$ en la ecuación$(x+4)^2 = 20$.

Ejercicio$\PageIndex{3}$

Resolver para$x :(x+7)^{2}=18$

Contestar: $-7+3 \sqrt{2},-7-3 \sqrt{2}$

Trinomios cuadrados perfectos revisitados

Recordemos la cuadratura de un atajo binomial.

Al cuadrado de un binomio

Si$a$ y$b$ son números reales, entonces: Es\[(a±b)^2 = a^2 ±2ab + b^2 \nonumber \] decir, cuadras el primer término, tomas el producto del primer y segundo términos y duplica el resultado, luego cuadras el tercer término.

Ejemplos de recordatorio:

\[\begin{aligned}(x+3)^{2} &=x^{2}+2(x)(3)+3^{2} \\ &=x^{2}+6 x+9 \end{aligned} \nonumber \]

\[\begin{aligned}(x-8)^{2} &=x^{2}-2(x)(8)+8^{2} \\ &=x^{2}-16 x+64 \end{aligned} \nonumber \]

Debido a que la factorización es “no multiplicar”, es una cuestión sencilla revertir el proceso de multiplicación y factorizar estos trinomios cuadrados perfectos.

\[x^{2}+6 x+9=(x+3)^{2} \nonumber \]

\[x^{2}-16 x+64=(x-8)^{2} \nonumber \]

Observe cómo en cada caso simplemente tomamos la raíz cuadrada del primer y último término.

Ejemplo$\PageIndex{4}$

Factorial cada uno de los siguientes trinomios:

$x^{2}-12 x+36$
$x^{2}+10 x+25$
$x^{2}-34 x+289$

Solución

Siempre que el primer y último término de un trinomio sean cuadrados perfectos, debemos sospechar que tenemos un trinomio cuadrado perfecto.

El primer y tercer término de$x^{2}-12 x+36$ son cuadrados perfectos. De ahí que tomemos sus raíces cuadradas e intentemos:\[x^{2}-12 x+36=(x-6)^{2} \nonumber \] Tenga en cuenta eso$2(x)(6)=12 x$, que es el término medio a la izquierda. La solución comprueba.
El primer y tercer término de$x^{2}+10 x+25$ son cuadrados perfectos. De ahí que tomemos sus raíces cuadradas e intentemos:\[x^{2}+10 x+25=(x+5)^{2} \nonumber \] Tenga en cuenta eso$2(x)(5)=10 x$, que es el término medio a la izquierda. La solución comprueba.
El primer y tercer término de$x^{2}-34 x+289$ son cuadrados perfectos. De ahí que tomemos sus raíces cuadradas e intentemos:\[x^{2}-34 x+289=(x-17)^{2} \nonumber \] Tenga en cuenta eso$2(x)(17)=34 x$, que es el término medio a la izquierda. La solución comprueba.

Ejercicio$\PageIndex{4}$

Factor:$x^2 + 30x + 225$

Contestar: $(x+15)^{2}$

Completando la Plaza

En esta sección comenzamos con el binomio$x^2 +bx$ y hacemos la pregunta “¿A qué valor constante debemos sumar para$x^2 + bx$ que el trinomio resultante sea un trinomio cuadrado perfecto?” La respuesta está en este procedimiento.

Completando la plaza

Para calcular la constante requerida para hacer$x^2 +bx$ un trinomio cuadrado perfecto:

Tome la mitad del coecient de$x : \dfrac{b}{2}$
Cuadrando el resultado del paso uno:$\left(\dfrac{b}{2}\right)^{2}=\dfrac{b^{2}}{4}$
Agregue el resultado del paso dos a$x^{2}+b x : x^{2}+b x+\dfrac{b^{2}}{4}$

Si sigues este proceso, el resultado será un trinomio cuadrado perfecto que se factorizará de la siguiente manera:

\[x^{2}+b x+\dfrac{b^{2}}{4}=\left(x+\dfrac{b}{2}\right)^{2} \nonumber \]

Ejemplo$\PageIndex{5}$

Dado$x^2 + 12 x$, completar el cuadrado para crear un trinomio cuadrado perfecto.

Solución

$x^2 + 12x$Compárelo$x^2 + bx$ y fíjelo$b = 12$.

Tome la mitad de$12: 6$
Cuadrando el resultado del paso uno:$6^2 = 36$
Agregue el resultado del paso dos a$x^2 + 12x: x^2 + 12x + 36$

Comprobar: Tenga en cuenta que el primer y último término de$x^2 +12x+36$ son cuadrados perfectos. Tomar las raíces cuadradas del primer y último término y factorizar de la siguiente manera:

\[x^{2}+12 x+36=(x+6)^{2} \nonumber \]

Tenga en cuenta que$2(x)(6) = 12x$, por lo que los cheques de mediano plazo.

Ejercicio$\PageIndex{5}$

Dado$x^2 + 16x$, completar el cuadrado para crear un trinomio cuadrado perfecto.

Contestar: $x^{2}+16 x+64=(x+8)^{2}$

Ejemplo$\PageIndex{6}$

Dado$x^2−3x$, completar el cuadrado para crear un trinomio cuadrado perfecto.

Solución

$x^2 −3x$Compárelo$x^2 + bx$ y fíjelo$b =−3$.

Tome la mitad de$-3 : -\dfrac{3}{2}$
Cuadrando el resultado del paso uno:$\left(-\dfrac{3}{2}\right)^{2}=\dfrac{9}{4}$
Agregue el resultado del paso dos a$x^{2}-3 x : x^{2}-3 x+\dfrac{9}{4}$

Comprobar: Tenga en cuenta que el primer y último término de$x^{2}-3 x+\dfrac {9}{4}$ son cuadrados perfectos. Tomar las raíces cuadradas del primer y último término y factorizar de la siguiente manera:

\[x^{2}-3 x+\dfrac{9}{4}=\left(x-\dfrac{3}{2}\right)^{2} \nonumber \]

Tenga en cuenta que$2(x)\left (\dfrac {3}{2} \right)=3 x$, por lo que los cheques de mediano plazo.

Ejercicio$\PageIndex{6}$

Dado$x^2 −5x$, completar el cuadrado para crear un trinomio cuadrado perfecto.

Contestar: $x^{2}-5 x+\dfrac {10}{4}=\left(x-\dfrac {5}{2} \right)^{2}$

Resolver ecuaciones completando el cuadrado

Considera la siguiente ecuación no lineal.

\[x^2 =2x +2 \nonumber \]

El enfoque estándar es hacer un lado cero y factor. \[x^2 −2x−2=0 \nonumber \]Sin embargo, uno rápidamente se da cuenta de que no hay un par entero cuyo producto es$ac = −2$ y cuya suma es$b = −2$. Entonces, ¿qué hace uno en esta situación? La respuesta es “Completa el cuadrado”.

Ejemplo$\PageIndex{7}$

Usa completar el cuadrado para ayudar a resolver$x^2 =2x + 2$.

Solución

Primero, muévase$2x$ hacia el lado izquierdo de la ecuación, manteniendo la constante$2$ en el lado derecho de la ecuación. \[x^2 −2x =2 \nonumber \]A la izquierda, tomar la mitad del coecient de$x: \left (\dfrac{1}{2} \right)(-2)=-1$. Cuadrando el resultado:$(-1)^{2}=1$. Agrega este resultado a ambos lados de la ecuación.

\[\begin{array}{l}{x^{2}-2 x+1=2+1} \\ {x^{2}-2 x+1=3}\end{array} \nonumber \]

Ahora podemos factorizar el lado izquierdo como un trinomio cuadrado perfecto.

\[(x-1)^{2}=3 \nonumber \]

Ahora, como en Ejemplos$\PageIndex{1}$,$\PageIndex{2}$, y$\PageIndex{3}$, podemos tomar la raíz cuadrada de ambos lados de la ecuación. Recuerden, hay dos raíces cuadradas.

\[x-1=\pm \sqrt{3} \nonumber \]

Por último,$1$ sumar a ambos lados de la ecuación.

\[x=1 \pm \sqrt{3} \nonumber \]

Así, la ecuación$x^2 =2x+ 2$ tiene dos respuestas,$x=1-\sqrt{3}$ y$x=1+\sqrt{3}$.

Consulta: Vamos a usar la calculadora para verificar las soluciones. Primero, almacene$1-\sqrt{3}$ en$\mathbf{X}$ (vea la imagen de la izquierda en la Figura$\PageIndex{4}$). Luego ingrese los lados izquierdo y derecho de la ecuación$x^2 =2 x + 2$ y compare los resultados (vea la imagen a la izquierda en la Figura$\PageIndex{4}$). De manera similar, comprueba la segunda respuesta$1+\sqrt{3}$ (ver la imagen de la derecha en la Figura$\PageIndex{4}$).

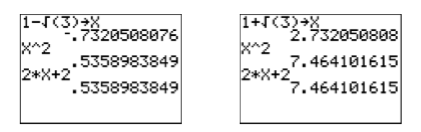
higo 8.3.4.png — Figura$\PageIndex{4}$: Comprobación$1-\sqrt{3}$ y$1+\sqrt{3}$ en la ecuación$x^2 =2x + 2$.

En ambos casos, tenga en cuenta que los lados izquierdo y derecho de$x^2 =2x+2$ producen el mismo resultado. De ahí que ambos$1-\sqrt{3}$ y$1+\sqrt{3}$ sean soluciones válidas de$x^2 =2x+2$.

Ejercicio$\PageIndex{7}$

Usa completar el cuadrado para ayudar a resolver$x^2 =3−6x$.

Contestar: $-3+2 \sqrt{3},-3-2 \sqrt{3}$

Ejemplo$\PageIndex{8}$

Resolver la ecuación$x^2 −8x−12 = 0$, tanto algebraica como gráficamente. Compara tu respuesta de cada método.

Solución

Primero, mueve la constante$12$ hacia el lado derecho de la ecuación.

\[\begin{aligned} x^{2}-8 x-12=0 & \quad \color {Red} \text { Original equation. } \\ x^{2}-8 x=12 & \quad \color {Red} \text { Add } 12 \text { to both sides. } \end{aligned} \nonumber \]

Toma la mitad del coecient de$x :(1 / 2)(-8)=-4$. Cuadrado:$(-4)^{2}=16$. Ahora agregue$16$ a ambos lados de la ecuación.

\[\begin{aligned} x^{2}-8 x+16 & =12+16 \quad \color {Red} \text { Add } 16 \text { to both sides. } \\ (x-4)^{2} & =28 \quad \color {Red} \text { Factor left-hand side. } \\ x-4 &=\pm \sqrt{28} \quad \color {Red} \text { There are two square roots. }\end{aligned} \nonumber \]
Tenga en cuenta que la respuesta no está en forma simple radical.

\[\begin{array}{rlrl}{x-4} & {=\pm \sqrt{4} \sqrt{7}} & {} & \color {Red} {\text { Factor out a perfect square. }} \\ {x-4} & {=\pm 2 \sqrt{7}} & {} & \color {Red} {\text { Simplify: } \sqrt{4}=2} \\ {x} & {=4 \pm 2 \sqrt{7}} & {} & \color {Red} {\text { Add } 4 \text { to both sides. }}\end{array} \nonumber \]

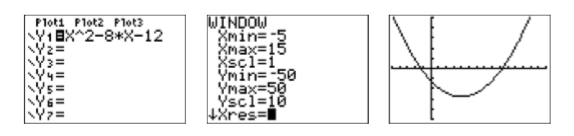
Solución gráfica: Ingrese la ecuación$y = x^2 − 8x − 12$ en$\mathbf{Y1}$ el menú Y= (vea la primera imagen en la Figura$\PageIndex{5}$). Después de alguna experimentación, nos fijamos en los parámetros VENTANA mostrados en la imagen media de la Figura$\PageIndex{5}$. Una vez que haya ingresado estos parámetros WINDOW, presione el botón GRAPAR para producir la imagen más a la derecha en la Figura$\PageIndex{5}$.

higo 8.3.5.png — Figura$\PageIndex{5}$: Dibujando la gráfica de$y = x^2 −8x−12$.

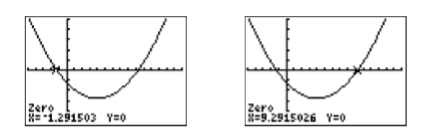
Estamos buscando soluciones de$x^2 −8x−12 = 0$, por lo que necesitamos ubicar donde la gráfica de$y = x^2 −8x−12$ intercepta el$x$ eje -eje. Es decir, tenemos que encontrar los ceros de$y = x^2 −8x−12$. Seleccione 2:cero en el menú CALC, mueva el cursor ligeramente hacia la izquierda de la primera$x$ intercepción y presione ENTRAR en respuesta a “Límite izquierdo”. Mueva el cursor ligeramente a la derecha de la primera$x$ intercepción y presione ENTRAR en respuesta a “Límite a la derecha”. Deje el cursor donde se sienta y presione ENTRAR en respuesta a “Guess”. La calculadora responde determinando la$x$ coordenada de la$x$ -intercepción, como se muestra en la primera imagen de la Figura$\PageIndex{6}$.

Repita el proceso para encontrar la segunda$x$ -intercepción de que$y = x^2−8x−12$ se muestra en la segunda imagen de la Figura$\PageIndex{6}$.

higo 8.3.6.png — Figura$\PageIndex{6}$: Cálculo de los ceros de$y = x^2 −8x−12$.

Reportando la solución en tu tarea: Duplica la imagen en la ventana de visualización de tu calculadora en tu página de tareas. Usa una regla para dibujar todas las líneas, pero a mano alzada cualquier curva.

Etiquete los ejes horizontal y vertical con$x$ y$y$, respectivamente (ver Figura$\PageIndex{7}$).
Coloca tus parámetros WINDOW al final de cada eje (ver Figura$\PageIndex{7}$).
Etiquete la gráfica con su ecuación (ver Figura$\PageIndex{7}$).
Deja caer líneas verticales discontinuas a través$x$ de cada intercepción. Sombra y etiquete los$x$ valores -de los puntos donde la línea vertical discontinua cruza el$x$ eje -eje. Estas son las soluciones de la ecuación$x^2−8x−12 = 0$ (ver Figura$\PageIndex{7}$).

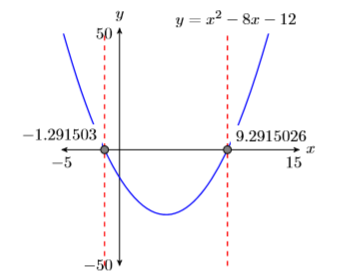
higo 8.3.7.png — Figura$\PageIndex{7}$: Reportando tu solución gráfica en tu tarea.

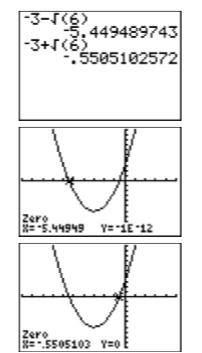
Así, la calculadora gráfica informa que las soluciones de$x^2 −8x−12 = 0$ son$x \approx-1.291503$ y$x \approx 9.2915026$.

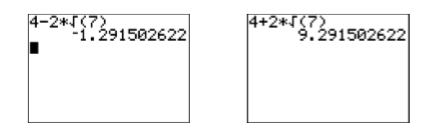
Comparando aproximaciones exactas y calculadoras: ¿Qué tan bien se comparan las soluciones de calculadora gráfica con las soluciones exactas$x=4-2 \sqrt{7}$ y$x=4+2 \sqrt{7}$? Después de ingresar cada uno en la calculadora (ver Figura$\PageIndex{8}$), ¡la comparación es excelente!

higo 8.3.8.png — Figura$\PageIndex{8}$: Aproximación de soluciones exactas$x=4-2 \sqrt{7}$ y$x=4+2 \sqrt{7}$.

Ejercicio$\PageIndex{8}$

Resuelve la ecuación$x^2 +6x + 3 = 0$ tanto algebraica como gráficamente, luego compara tus respuestas.

Contestar

$-3-\sqrt{6},-3+\sqrt{6}$

$Ejercicio 8.3.8.png$

Search

Text Color

Text Size

Margin Size

Font Type