1.4: Suma y resta números enteros
- Page ID
- 110504
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Usar negativos y opuestos
- Simplificar: expresiones con valor absoluto
- Agregar enteros
- Restar enteros
Una introducción más completa a los temas tratados en esta sección se puede encontrar en el capítulo Preálgebra, Enteros.
Usar negativos y opuestos
Nuestro trabajo hasta el momento sólo ha incluido los números de conteo y los números enteros. Pero si alguna vez has experimentado una temperatura por debajo de cero o has sobregirado accidentalmente tu cuenta corriente, ya estás familiarizado con los números negativos. Los números negativos son números menores que\(0\). Los números negativos están a la izquierda de cero en la recta numérica. Ver Figura\(\PageIndex{1}\).
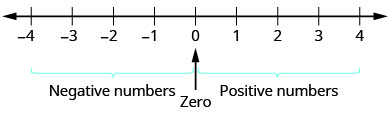
Las flechas en los extremos de la recta numérica indican que los números siguen para siempre. No hay mayor número positivo, y no hay menor número negativo.
¿El cero es un número positivo o negativo? Los números mayores que cero son positivos y los números menores que cero son negativos. El cero no es ni positivo ni negativo.
Considera cómo se ordenan los números en la línea numérica. Pasando de izquierda a derecha, los números aumentan de valor. Al ir de derecha a izquierda, los números disminuyen de valor. Ver Figura\(\PageIndex{2}\).
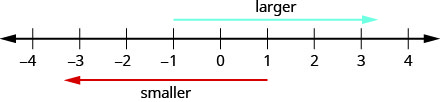
Hacer la actividad de Matemáticas Manipulativas “Línea numérica Parte 2” te ayudará a desarrollar una mejor comprensión de los enteros.
Recuerda que usamos la notación:
\(a \lt b\)(leer “\(a\)es menor que\(b\)”) cuando\(a\) está a la izquierda de\(b\) en la recta numérica.
\(a \gt b\)(léase “\(a\)es mayor que\(b\)”) cuando\(a\) está a la derecha de\(b\) en la recta numérica.
Ahora necesitamos extender la línea numérica que mostraba los números enteros para incluir también números negativos. Los números marcados por puntos en la Figura\(\PageIndex{3}\). se llaman los enteros. Los enteros son los números\(...−3, −2, −1, 0, 1, 2, 3…\)

Ordene cada uno de los siguientes pares de números, usando\(<\) o\(>\):
- \(14 \; \_\_\_\; 6\)
- \(-1\; \_\_\_ \;9\)
- \(-1\; \_\_\_ -4\)
- \(\;\; 2 \;\_\_\_ -20\)
Solución:
Puede ser útil referirse a la línea numérica que se muestra.

Figura\(\PageIndex{4}\)
\ (\ begin {alinear*} 1. \ quad & 14\;\ _\ _\ _\; 6\\ [4pt]
& 14 > 6 &&\ text {\(14\)está a la derecha de\(6\) en la línea numérica.}\\ [8pt]
2. \ quad & -1\;\ _\ _\ _\; 9\\ [4pt]
& -1 < 9 &&\ text {\(-1\)está a la izquierda de\(9\) en la línea numérica.}\\ [8pt]
3. \ quad & -1\;\ _\ _\ _-4\\ [4pt]
& -1 > -4 &&\ text {\(-1\)está a la derecha de\(-4\) en la línea numérica.}\\ [8pt]
4. \ quad & 2\;\ _\ _\ _-20\\ [4pt]
& 2 > -20 &&\ text {\(2\)está a la derecha de\(-20\) en la línea numérica.} \
\ end {alinear*}\)
Ordene cada uno de los siguientes pares de números, usando\(<\) or \(>\):
- \(15 \; \_\_\_\; 7\)
- \(-2 \; \_\_\_\; 5\)
- \(-3 \; \_\_\_\; -7\)
- \(5 \; \_\_\_\; -17\)
- Answer
-
- \(<\)
- \(>\)
- \(<\)
- \(>\)
Ordene cada uno de los siguientes pares de números, usando\(<\) o\(>\):
- \(8 \; \_\_\_\; 13\)
- \(3 \; \_\_\_\; -4\)
- \(-5 \; \_\_\_\; -2\)
- \(9 \; \_\_\_\; -21\)
- Responder
-
- \(<\)
- \(>\)
- \(<\)
- \(>\)
Es posible que hayas notado que, en la recta numérica, los números negativos son una imagen especular de los números positivos, con cero en el medio. Debido a que los números\(2\) y\(−2\) están a la misma distancia de cero, se les llama opuestos s. Lo opuesto de\(2\) es\(−2\), y lo contrario de\(−2\) es\(2\).
Lo contrario de un número es el número que está a la misma distancia de cero en la recta numérica pero en el lado opuesto de cero.
La figura\(\PageIndex{5}\) ilustra la definición.

A veces en álgebra el mismo símbolo tiene diferentes significados. Al igual que algunas palabras en inglés, el significado específico se vuelve claro al observar cómo se usa. Has visto el símbolo “\(−\)” utilizado de tres formas distintas.
\ [\ begin {align*} &10 − 4\ quad\ text {Entre dos números, indica la operación de}\ textit {resta}.\\ &\ qquad\ qquad\ text {Leemos} 10 - 4\,\ text {como “} 10\,\ text {como “} 10\,\ text {menos}\, 4. \ text {”}\\ [5pt]
&-8\ quad\ text {Delante de un número, indica un}\ textit {negativo}\ text {número.}\\ &\ qquad\ qquad\ text {Leemos} -8\ text {como “ocho negativo”.}\\ [5pt]
&-x\ quad\ text {Delante de una variable, indica el}\ textit {opuesto.}\\ &\ qquad\ qquad\ text {Leemos} -x\ text {como “lo contrario de} x\ text {”}\\ [5pt]
&- (-2)\ quad\ text {Aquí hay dos signos “−”.} \\
&\ qquad\ qquad\ text {El que está entre paréntesis nos dice que el número es negativo} 2. \\
&\ qquad\ qquad\ text {El que está fuera de los paréntesis nos dice que tomemos el}\ textit {opuesto}\ texto {de} −2. \\
&\ qquad\ qquad\ text {Leemos} − (−2)\ text {como “lo opuesto de dos negativos”.} \ end {alinear*}\]
\(−a\)significa lo contrario del número\(a\).
La notación\(−a\) se lee como “lo contrario de”\(a\).
Encuentra:
- lo contrario de\(7\)
- lo contrario de\(−10\)
- lo contrario de\(−(−6)\)
Solución:
1. \( \quad −7\)es la misma distancia de\(0\) como\(7\), pero en el lado opuesto de\(0\). Lo contrario de\(7\) es\(-7\).

2. \( \quad 10\)es la misma distancia de\(0\) como\(−10\), pero en el lado opuesto de\(0\). Lo contrario de\(-10\) es\(10\).

3. \(\quad\)Lo contrario de\(-(-6)\) es\(-6\).

Encuentra:
- lo contrario de\(4\)
- the opposite of \(−3\)
- \(−(−1)\)
- Answer
-
- \(-4\)
- \(3\)
- \(1\)
Encuentra:
- lo contrario de\(8\)
- lo contrario de\(−5\)
- \(−(−5)\)
- Responder
-
- \(-8\)
- \(5\)
- \(5\)
Nuestro trabajo con los opuestos nos da una forma de definir los enteros. Los números enteros y sus opuestos se llaman los enteros. Los enteros son los números\(…−3,−2,−1,0,1,2,3…\)
Los números enteros y sus opuestos se llaman los enteros.
Los enteros son los números
\[…−3,−2,−1,0,1,2,3… \nonumber \]
Al evaluar lo contrario de una variable, debemos ser muy cuidadosos. Sin saber si la variable representa un número positivo o negativo, no sabemos si −x−x es positivo o negativo. Esto lo podemos ver en Ejemplo\(\PageIndex{1}\).
Evaluar
- \(-x\), cuando\(x = 8\)
- \(-x\), cuando\(x = -8\)
Solución:
-

-x 
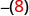
Escribe lo contrario de 8. -8 -

-x 
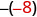
Escribe lo contrario de -8. 8
Evaluar\(-n\), when
- \(n = 4\)
- \(n = -4\)
- Answer
-
- \(-4\)
- \(4\)
Evaluar\(-m\), cuando
- \(m = 11\)
- \(m = -11\)
- Responder
-
- \(-11\)
- \(11\)
Simplificar: Expresiones con Valor Absoluto
Vimos que números como\(2\) y\(−2\) son opuestos porque están a la misma distancia de\(0\) en la recta numérica. Ambos son dos unidades de\(0\). La distancia entre\(0\) y cualquier número en la línea numérica se llama el valor absoluto de ese número.
El valor absoluto de un número es su distancia desde\(0\) la línea numérica.
El valor absoluto de un número\(n\) se escribe como\(|n|\).
Por ejemplo,
- \(−5\)es\(5\) unidades lejos de\(0\), entonces\(|−5|=5\).
- \(5\)es\(5\) unidades lejos de\(0\), entonces\(|5|=5\).
La figura\(\PageIndex{6}\) ilustra esta idea.
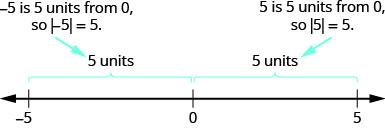
El valor absoluto de un número nunca es negativo (porque la distancia no puede ser negativa). El único número con valor absoluto igual a cero es el número cero en sí, porque la distancia de\(0\) a\(0\) en la recta numérica es cero unidades.
\(|n| \geq 0\)para todos los números
¡Los valores absolutos siempre son mayores o iguales a cero!
Los matemáticos lo dicen con mayor precisión, “los valores absolutos siempre son no negativos”. No negativo significa mayor o igual a cero.
Simplificar:
- \(|3|\)
- \(|-44|\)
- \(|0|\)
Solución:
El valor absoluto de un número es la distancia entre el número y cero. La distancia nunca es negativa, por lo que el valor absoluto nunca es negativo.
- \( |3| = 3\)
- \(|-44| = 44\)
- \( |0| = 0\)
Simplificar:
- \(|4|\)
- \(|-28|\)
- \(|0|\)
- Answer
-
- \(4\)
- \(28\)
- \(0\)
Simplificar:
- \(|-13|\)
- \(|47|\)
- Responder
-
- \(13\)
- \(47\)
En el siguiente ejemplo, ordenaremos expresiones con valores absolutos. Recuerda, ¡los números positivos siempre son mayores que los números negativos!
Rellena\(<, >, \text{or} =\) para cada uno de los siguientes pares de números:
- \(|−5| \; {\underline{\hspace {2 em}}} \;−|−5|\)
- \(8 \;{\underline{\hspace {2 em}}} \;−|−8|\)
- \(-9 \;{\underline{\hspace {2 em}}} \;−|−9|\)
- \(-(-16) \;{\underline{\hspace {2 em}}}\; −|−16|\)
Solución:
\(\begin{array} {llll} {\text{Simplification}} &{|-5|} & {\underline{\hspace {2 em}}} &{-|-5|} \\ {\text{Order.}} &{5} &{\underline{\hspace {2 em}}} &{-5} \\ {} &{5} &{>} &{-5} \\ {} &{|-5|} &{>} &{-|-5|} \\ \end{array}\)
\(\begin{array} {llll} {\text{Simplification}} &{8} & {\underline{\hspace {2 em}}} &{-|-8|} \\ {\text{Order.}} &{8} &{\underline{\hspace {2 em}}} &{-8} \\ {} &{8} &{>} &{-8} \\ \text{so }\\ {} & {|8|} &{>} &{-|-8|} \\ \end{array}\)
\(\begin{array} {llll} {\text{Simplification}} &{-9} & {\underline{\hspace {2 em}}} &{-|-9|} \\ {\text{Order.}} &{-9} &{\underline{\hspace {2 em}}} &{-9} \\ {} &{-9} &{=} &{-9} \\ \text{so } \\ {} & {-9} &{=} &{-|-9|} \\ \end{array}\)
\(\begin{array} {llll} {\text{Simplification}} &{-(-16)} & {\underline{\hspace {2 em}}} &{-|16|} \\ {\text{Order.}} &{16} &{\underline{\hspace {2 em}}} &{-16} \\ {} &{16} &{>} &{-16} \\ \text{so } \\ {} & {-(-16)} &{>} &{-|-16|} \\ \end{array}\)
Rellenar\(<, >, \text{or} =\) for each of the following pairs of numbers:
- \(|−9| \;{\underline{\hspace {2 em}}} \; −|−9|\)
- \(2 \;{\underline{\hspace {2 em}}} \; −|−2|\)
- \(-8 \;{\underline{\hspace {2 em}}} \; −|−8|\)
- \(-(-9) \;{\underline{\hspace {2 em}}} \; −|−9|\)
- Answer
-
- \(>\)
- \(>\)
- \(<\)
- \(>\)
Rellena\(<, >, \text{or} =\) para cada uno de los siguientes pares de números:
- \(7 \;{\underline{\hspace {2 em}}} \; −|−7|\)
- \(-(-10) \;{\underline{\hspace {2 em}}} \; −|−10|\)
- \(|-4| \;{\underline{\hspace {2 em}}} \; −|−4|\)
- \(-1 \;{\underline{\hspace {2 em}}} \; |−1|\)
- Responder
-
- \(>\)
- \(>\)
- \(>\)
- \(<\)
Ahora agregamos barras de valor absoluto a nuestra lista de símbolos de agrupación. Cuando usamos el orden de las operaciones, primero simplificamos dentro de las barras de valor absoluto tanto como sea posible, luego tomamos el valor absoluto del número resultante.
\[\begin{array} {llll} {\text{Parentheses}} &{()} & {\text{Braces}} & {\{\}} \\ {\text{Brackets}} &{[\space]} &{\text{Absolute}} &{|\space|} \\ \end{array} \nonumber\]
En el siguiente ejemplo, primero simplificamos las expresiones dentro de las barras de valor absoluto, al igual que hacemos con los paréntesis.
Simplificar:\(24 - |19 - 3(6 - 2)|\)
Solución:
\[\begin{array} {ll} {} &{24 - |19 - 3(6 - 2)|} \\ {\text{Work inside parentheses first: subtract } 2\space \text{from } 6} &{24 - |19 - 3(4)|} \\ {\text{Multiply }3(4)} &{24 - |19 - 12|} \\ {\text{Subtract inside the absolute value bars. }} &{24 - |7|} \\ {\text{Take the absolute value.}} &{24 - 7} \\ {\text{Subtract.}} &{17} \end{array}\nonumber\]
Simplificar:\(19 - |11 - 4(3 - 1)|\)
- Answer
-
\(16\)
Simplificar:\(9 - |8 - 4(7 - 5)|\)
- Responder
-
\(9\)
Evaluar:
- \(|x|\)cuando\(x = -35\)
- \(|y|\)cuando\(y = -20\)
- \(-|u|\)cuando\(u = 12\)
- \(-|p|\)cuando\(p = -14\)
Solución:
1. \(|x|\)cuando\(x = -35\)
\(\begin{array} {ll} {} &{|x|} \\ {\text{Substitute } -35 \space \text{for }x} &{|-35|} \\ {\text{Take the absolute value.}} &{35} \end{array}\)
2. \(|y|\)cuando\(y = -20\)
\(\begin{array} {ll} {} &{|-y|} \\ {\text{Substitute } -20 \space \text{for }y} &{|-(-20)|} \\ {\text{Simplify}} &{|20|} \\ {\text{Take the absolute value.}} &{20} \end{array}\)
3. \(-|u|\)cuando\(u = 12\)
\(\begin{array} {ll} {} &{-|u|} \\ {\text{Substitute } 12 \space \text{for }u} &{|-12|} \\ {\text{Take the absolute value.}} &{-12} \end{array}\)
4. \(-|p|\)cuando\(p = -14\)
\(\begin{array} {ll} {} &{-|p|} \\ {\text{Substitute } -14 \space \text{for }p} &{-|-14|} \\ {\text{Take the absolute value.}} &{-14} \end{array}\)
Evaluar:
- \(|x|\) when \(x = -17\)
- \(|y|\) when \(y = -39\)
- \(-|m|\) when \(m = 22\)
- \(-|p|\) when \(p = -11\)
- Answer
-
- \(17\)
- \(39\)
- \(-22\)
- \(-11\)
Evaluar:
- \(|y|\)cuando\(y = -23\)
- \(|-y|\)cuando\(y = -21\)
- \(-|n|\)cuando\(n = 37\)
- \(-|q|\)cuando\(q = -49\)
- Responder
-
- \(23\)
- \(21\)
- \(-37\)
- \(-49\)
Agregar números enteros
La mayoría de los estudiantes se sienten cómodos con los hechos de suma y resta para números positivos. Pero hacer sumar o restar tanto con números positivos como negativos puede ser más desafiante.
Hacer la actividad de Matemáticas Manipulativas “Adición de números firmados” te ayudará a desarrollar una mejor comprensión de sumar enteros”.
Utilizaremos dos contadores de color para modelar la suma y resta de negativos para que puedas visualizar los procedimientos en lugar de memorizar las reglas.
Dejamos que un color (azul) represente positivo. El otro color (rojo) representará los negativos. Si tenemos un contador positivo y otro negativo, el valor del par es cero. Forman un par neutro. El valor de este par neutro es cero.
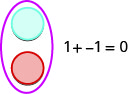
Usaremos los contadores para mostrar cómo agregar los cuatro hechos de adición usando los números\(5, −5\) y\(3,−3\).
\[\begin{array} {llll} {5 + 3} &{-5 + (-3)} &{-5 + 3} &{5 + (-3)} \end{array} \nonumber \]
Para agregar\(5+3\), nos damos cuenta de que eso\(5+3\) significa la suma de\(5\) y\(3\).
| Empezamos con\(5\) aspectos positivos. |  |
| Y luego agregamos\(3\) aspectos positivos. |  |
| Ahora tenemos\(8\) aspectos positivos. La suma de\(5\) y\(3\) es\(8\). |  |
Ahora vamos a añadir\(−5 + (−3)\). Esté atento a las similitudes con el último ejemplo\(5 + 3 = 8\).
Para agregar\(−5 + (−3)\), nos damos cuenta de que esto significa la suma de\(−5\) y\(−3\).
| Empezamos con\(5\) los negativos. |  |
| Y luego agregamos\(3\) negativos. |  |
| Ahora tenemos\(8\) negativo. La suma de\(-5\) y\(-3\) es\(-8\). |  |
¿De qué manera fueron similares estos dos primeros ejemplos?
- El primer ejemplo agrega\(5\) positivos y\(3\) positivos, ambos positivos.
- El segundo ejemplo agrega\(5\) negativos y\(3\) negativos, ambos negativos.
En cada caso obtuvimos\(8\) —ya sea\(8\) positivos o\(8\) negativos.
Cuando los letreros eran los mismos, los mostradores eran todos del mismo color, y así los agregamos.

Agregar:
- \(1 + 4\)
- \(-1 + (-4)\)
Solución:
1. 
\(1\)positivo más\(4\) positivo es\(5\) positivo.
2. 
\(1\)negativos más\(4\) negativos son\(5\) negativos.
Agregar:
- \(2 + 4\)
- \(-2 + (-4)\)
- Answer
-
- \(6\)
- \(-6\)
Agregar:
- \(2 + 5\)
- \(-2 + (-5)\)
- Responder
-
- \(7\)
- \(-7\)
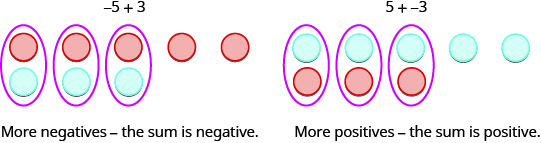
Entonces, ¿qué pasa cuando los signos son diferentes? Vamos a agregar\(−5+3\). Nos damos cuenta de que esto significa la suma de\(−5\) y\(3\). Cuando los mostradores eran del mismo color, los colocamos en fila. Cuando los contadores son de un color diferente, los alineamos uno debajo del otro.
| \(-5 + 3\)significa la suma de\(-5\) y\(3\). | |
| Empezamos con\(5\) los negativos. |  |
| Y luego agregamos\(3\) aspectos positivos. |  |
| Eliminamos cualquier par neutro. | 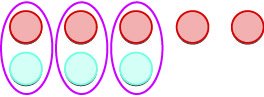 |
| Nos quedan\(2\) negativos. |  |
| La suma de\(-5\) y\(3\) es\(-2\). | \(-5 + 3 = 2\) |
Observe que hubo más negativos que positivos, por lo que el resultado fue negativo.
Ahora agreguemos la última combinación,\(5+(−3)\).
| \(5 + (-3)\)significa la suma de\(-5\) y\(-3\). | |
| Empezamos con\(5\) aspectos positivos. |  |
| Y luego agregamos\(3\) negativos. | 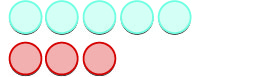 |
| Eliminamos cualquier par neutro. | 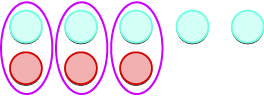 |
| Nos quedan\(2\) positivos. |  |
| La suma de\(5\) y\(-3\) es\(2\). | \(5 + (-3) = 2\) |
Cuando usamos contadores para modelar la suma de enteros positivos y negativos, es fácil ver si hay más contadores positivos o más negativos. Entonces sabemos si la suma será positiva o negativa.
Agregar:
- \(-1 + 5\)
- \(1 + (-5)\)
Solución:
1. \(-1 + 5\)

Hay más positivos, por lo que la suma es positiva.
Entonces,\(-1 + 5 = 4\).
2. \(1 + (-5)\)

Hay más negativos, por lo que la suma es negativa.
Entonces,\(1 + (-5) = -4\)
Agregar:
- \(-2 + 4\)
- \(2 + (-4)\)
- Answer
-
- \(2\)
- \(-2\)
Agregar:
- \(-2 + 5\)
- \(2 + (-5)\)
- Responder
-
- \(3\)
- \(-3\)
Ahora que hemos agregado pequeños enteros positivos y negativos con un modelo, podemos visualizar el modelo en nuestra mente para simplificar problemas con cualquier número.
Cuando necesitas agregar números como\(37+(−53)\), realmente no quieres tener que contar contadores\(37\) azules y contadores\(53\) rojos. Con el modelo en tu mente, ¿puedes visualizar lo que harías para resolver el problema?
Cuadro mostradores\(37\) azules con mostradores\(53\) rojos alineados debajo. Dado que habría más contadores rojos (negativos) que contadores azules (positivos), la suma sería negativa. ¿Cuántos contadores rojos más habría? Porque\(53−37=16\), hay\(16\) más contadores rojos.
Por lo tanto, la suma de\(37+(−53)\) es\(−16\).
\[37+(−53)=−16\nonumber\]
Intentemos con otro. Vamos a agregar\(−74+(−27)\). De nuevo, imagina contadores\(74\) rojos y\(27\) más contadores rojos, así tendríamos contadores\(101\) rojos. Esto quiere decir que la suma es\(−101\).
\[−74+(−27)=−101\nonumber\]
Veamos de nuevo los resultados de sumar las diferentes combinaciones de\(5,−5\) y\(3, -3\).
\[\begin{array} {ll} {5 + 3=8} &{-5 + (-3)=-8} \\{\text{both positive, sum positive}} &{\text{both positive, sum positive}} \end{array}\nonumber\]
Cuando los signos son los mismos, los contadores serían todos del mismo color, así que agréguelos.
\[\begin{array} {ll} {5 + 3=-2} &{-5 + (-3)=2} \\{\text{different signs, more negatives, sum negative}} &{\text{different signs, more positives, sum positive}} \end{array}\nonumber\]
Cuando los signos son diferentes, algunos de los contadores harían pares neutros, así que restan para ver cuántos quedan.
Visualice el modelo a medida que simplifica las expresiones en los siguientes ejemplos.
Simplificar:
- \(19 + (-47)\)
- \(-14 + (-36)\)
Solución:
1. Dado que los signos son diferentes, restamos\(19\) de\(47\). La respuesta será negativa porque hay más negativos que positivos.
\(\text{Add.} \qquad 19 + (-47) = -28\)
2. Ya que los signos son los mismos, agregamos. La respuesta será negativa porque hay más negativos que positivos.
\(\text{Add.} \qquad-14 + (-36) = -50\)
Simplificar:
- \(-31 + (-19)\)
- \(15 + (-32)\)
- Answer
-
- \(-50\)
- \(-17\)
Simplificar:
- \(-42 + (-28)\)
- \(25 + (-61)\)
- Responder
-
- \(-70\)
- \(-36\)
Las técnicas utilizadas hasta ahora se extienden a problemas más complicados, como los que hemos visto antes. ¡Recuerda seguir el orden de las operaciones!
Simplificar:
\(-5 + 3(-2 + 7)\)
Solución:
\[\begin{array} {ll} {} &{-5 + 3(-2 + 7)} \\ {\text{Simplify inside the parenthesis}} &{-5 + 3(5)} \\{\text{Multiply}} &{-5 + 15} \\{\text{add left to right}} &{10} \end{array}\nonumber\]
Simplificar:
\(-2 + 5(-4 + 7)\)
- Answer
-
\(13\)
Simplificar:
\(-4 + 2(-3 + 5)\)
- Responder
-
\(0\)
Restar enteros
Hacer la actividad de Matemáticas Manipulativas “Resta de números firmados” te ayudará a desarrollar una mejor comprensión de restar enteros.
Seguiremos utilizando contadores para modelar la resta. Recuerde, los contadores azules representan números positivos y los contadores rojos representan números negativos.
Quizás cuando eras más joven, leías “\(5−3\)” como “\(5\)llevar”\(3\). Cuando usas contadores, ¡puedes pensar en restar de la misma manera!
Modelaremos los cuatro hechos de resta usando los números\(5\) y\(3\).
\[\begin{array} {llll} {5 - 3} &{-5 - (-3))} &{-5 -3} &{5 - (-3)} \end{array}\nonumber\]
Para restar\(5−3\), reafirmamos el problema como “\(5\)llevar”\(3\).
| Empezamos con\(5\) aspectos positivos. |  |
| Nosotros 'llevamos'\(3\) positivos. |  |
| Nos quedan\(2\) positivos. | |
| La diferencia de\(5\) y\(3\) es\(2\). | \(2\) |
Ahora vamos a restar\(−5−(−3)\). Esté atento a las similitudes con el último ejemplo\(5−3=2\).
Para restar\(−5−(−3)\), lo reafirmamos como “\(–5\)llevar\(–3\)”
| Empezamos con\(5\) los negativos. |  |
|
Nosotros 'llevamos'\(3\) negativos. |
 |
| Nos quedan\(2\) negativos. | |
| La diferencia de\(-5\) y\(-3\) es\(-2\). |
\(-2\) |
Observe que estos dos ejemplos son muy parecidos: El primer ejemplo, restamos 3 positivos de 5 positivos y terminamos con 2 positivos.
En el segundo ejemplo, restamos 3 negativos de 5 negativos y terminamos con 2 negativos.
Cada ejemplo utilizó contadores de un solo color, y el modelo “take away” de resta fue fácil de aplicar.
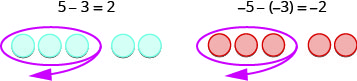
Resta:
- \(7 - 5\)
- \(-7 - (-5)\)
Solución:
- \[\begin{array} {ll} {7 - 5} \\ {2}&{\text{Take }5\space \text{positives from }7 \space \text{positives and get }2\space \text{positives}} & \end{array}\nonumber\]
- \[\begin{array} {ll} {-7 - (-5)} \\ {-2} &{\text{Take }5\space \text{negatives from }7 \space \text{negatives and get }2\space \text{negatives}} \end{array}\nonumber\]
Resta:
- \(6 - 4\)
- \(-6 - (-4)\)
- Answer
-
- \(2\)
- \(-2\)
Resta:
- \(7 - 4\)
- \(-7 - (-4)\)
- Responder
-
- \(3\)
- \(-3\)
¿Qué pasa cuando tenemos que restar un número positivo y otro negativo? Tendremos que usar contadores blancos y rojos así como algunos pares neutros. Agregar un par neutro no cambia el valor. Es como cambiar trimestres a níqueles, el valor es el mismo, pero se ve diferente.
- Para restar\(−5−3\), lo reafirmamos como\(−5\) take away\(3\).
Empezamos con\(5\) los negativos. Tenemos que quitar\(3\) los positivos, pero no tenemos ningún positivo que quitar.
Recuerda, un par neutro tiene valor cero. Si sumamos\(0\) a\(5\) su valor sigue siendo\(5\). Agregamos pares neutros a\(5\) los negativos hasta que obtenemos\(3\) positivos para llevar.
| \(-5 -3\)significa\(-5\) llevar\(3\) | |
| Empezamos con\(5\) los negativos. |  |
| Ahora agregamos los neutrales necesarios para obtener\(3\) positivos. |  |
| Eliminamos\(3\) los positivos. | 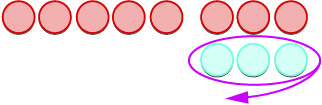 |
| Nos quedan\(8\) los negativos. |  |
| La diferencia de\(-5\) y\(3\) es\(-8\). | \(-5 - 3 = -8\) |
Y ahora, el cuarto caso,\(5−(−3)\). Empezamos con\(5\) aspectos positivos. Tenemos que quitar\(3\) los negativos, pero no hay negativos que quitar. Entonces agregamos pares neutros hasta que tengamos\(3\) negativos para llevar.
| \(5 -(-3)\)significa\(5\) llevar\(-3\) | |
| Empezamos con\(5\) aspectos positivos. |  |
| Ahora agregamos los pares neutros necesarios. |  |
| Eliminamos\(3\) los negativos. | 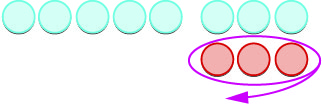 |
| Nos quedamos con\(8\) aspectos positivos. |  |
| La diferencia de\(5\) y\(-3\) es\(8\). | \(5 - (-3) = 8\) |
Resta:
- \(-3 -1\)
- \(3 - (-1)\)
Solución:
1.
|
Toma 1 positivo del par neutro agregado. |
  |
\(\begin{array} {l} {-3 -1} \\ {-4} \end{array}\) |
|
Toma 1 negativo del par neutro agregado. |
  |
\(\begin{array} {l} {3 - (-1)} \\ {4} \end{array}\) |
Resta:
- \(-6 -4\)
- \(6 - (-4)\)
- Answer
-
- \(-10\)
- \(10\)
Resta:
- \(-7-4\)
- \(7 - (-4)\)
- Responder
-
- \(-11\)
- \(11\)
¿Te has dado cuenta de que la resta de números firmados se puede hacer sumando lo contrario? En Ejercicio\(\PageIndex{33}\),\(−3−1\) es lo mismo que\(−3+(−1)\) y\(3−(−1)\) es lo mismo que\(3+1\). A menudo verás esta idea, la propiedad de resta, escrita de la siguiente manera:
\[a−b=a+(−b) \nonumber\]
Restar un número es lo mismo que sumar su opuesto.
Mira estos dos ejemplos.
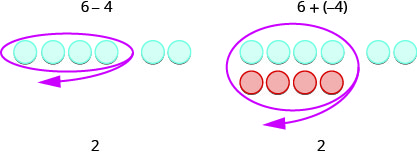
Por supuesto, cuando tienes un problema de resta que solo tiene números positivos\(6−4\), como, solo haces la resta. Ya sabías restar hace\(6−4\) mucho tiempo. Pero saber eso\(6−4\) da la misma respuesta que\(6+(−4)\) ayuda cuando estás restando números negativos. ¡Asegúrate de entender cómo\(6−4\) y\(6+(−4)\) dar los mismos resultados!
Simplificar:
- \(13 - 8 \space \text{and } 13 + (-8)\)
- \(-17 - 9 \space \text{and } -17 + (-9)\)
Solución:
- \(\begin{array} {llll} {\text{Subtract.}} &{13 - 8} &{\text{and}} &{13 + (-8)} \\ {} &{5} &{} &{5} \end{array}\)
- \(\begin{array} {llll} {\text{Subtract.}} &{-17 - 9} &{\text{and}} &{-17 + (-9)} \\ {} &{-26} &{} &{-26} \end{array}\)
Simplificar:
- \(21 - 13 \space \text{and } 21 + (-13)\)
- \(-11 - 7 \space \text{and } -11 + (-7)\)
- Answer
-
- \(8\)
- \(-18\)
Simplificar:
- \(15 - 7 \space \text{and } 15 + (-7)\)
- \(-14 - 8 \space \text{and } -14 + (-8)\)
- Responder
-
- \(8\)
- \(-22\)
Mira lo que sucede cuando restamos un negativo.

¡Restar un número negativo es como sumar un positivo!
A menudo verás esto escrito como\(a−(−b)=a+b\).
¿Eso también funciona para otros números? Hagamos el siguiente ejemplo y veamos.
Simplificar:
- \(9 - (-15) \space \text{and } 9 + 15\)
- \(-7 - (-4) \space \text{and } -7 + 4\)
Solución:
- \(\begin{array} {lll} {} &{9 - (-15)} &{9 + 15} \\ {\text{Subtract}} &{24} &{24} \end{array}\)
- \(\begin{array} {lll} {} &{-7 - (-4)} &{-7 + 4} \\ {\text{Subtract}} &{-3} &{-3} \end{array}\)
Simplificar:
- \(6 - (-13) \space \text{and } 6 + 13\)
- \(-5 - (-1) \space \text{and } -5 + 1\)
- Answer
-
- \(19\)
- \(-4\)
Simplificar:
- \(4 - (-19) \space \text{and } 4 + 19\)
- \(-4 - (-7) \space \text{and } -4 + 7\)
- Responder
-
- \(23\)
- \(3\)
Volvamos a ver los resultados de restar las diferentes combinaciones de\(5,−5\) y\(3,−3\).
\[\begin{array} {l} {5 - 3} &{-5 - (-3)} \\ {2} &{-2} \\ {5\space\text{positives take away }3\space\text{positives}} &{5\space\text{negatives take away }3\space\text{negatives}} \\ {2\space\text{positives}} &{2\space\text{negatives}} \end{array}\nonumber\]
Cuando hubiera suficientes contadores del color para llevar, restar.
\[\begin{array} {l} {-5 - 3} &{5 - (-3)} \\ {-8} &{8} \\ {5\space\text{negatives, want to take away }3\space\text{positives}} &{5\space\text{positives, want to take away }3\space\text{negatives}} \\ {\text{need neutral pairs}} &{\text{need neutral pairs}} \end{array}\nonumber\]
Cuando no hubiera suficientes contadores del color para llevar, agregue.
¿Qué sucede cuando hay más de tres enteros? Simplemente usamos el orden de las operaciones como de costumbre.
Simplificar:
\(7 - (-4 -3) - 9\)
Solución:
\[ \begin{array} {ll} {} &{7 - (-4 - 3) - 9} \\ {\text{Simplify inside the parenthesis first.}} &{7 - (-7) - 9} \\ {\text{Subtract left to right.}} &{14 - 9} \\ {\text{Subtract}} &{5} \end{array}\nonumber\]
Simplificar:
\(8−(−3−1)−9\)
- Answer
-
\(3\)
Simplificar:
\(12−(−9−6)−14\)
- Responder
-
\(12\)
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con sumar y restar números enteros. Necesitará habilitar Java en su navegador web para usar las aplicaciones.
Conceptos clave
- Adición de números enteros positivos y negativos
\[\begin{array} {ll} {5 + 3} &{-5+(-3)} \\ {8} &{-8} \\ {\text{both positive,}} &{\text{both negative,}} \\ {\text{sum positive}} &{\text{sum negative}} \end{array}\nonumber\]
\[\begin{array} {ll} {-5 + 3} &{5+(-3)} \\ {-2} &{2} \\ {\text{different signs,}} &{\text{different signs,}} \\ {\text{more negatives}} &{\text{more positives}} \\ {\text{sum negative}} &{\text{sum positive}} \end{array}\nonumber\]
- Propiedad de Valor Absoluto:
\(|n| \geq 0\)para todos los números. ¡Los valores absolutos siempre son mayores o iguales a cero!
- Resta de números enteros
\[\begin{array} {ll} {5 - 3} &{-5-(-3)} \\ {2} &{-2} \\ {5\space\text{positives}} &{5\space\text{negatives}} \\ {\text{take away 3 positives}} &{\text{take away 3 negatives}} \\ {\text{2 positives}} &{\text{2 negatives}} \end{array}\nonumber\]
\[\begin{array} {ll} {-5 - 3} &{5-(-3)} \\ {-8} &{8} \\ {\text{5 negatives, want to}} &{\text{5 positives, want to}} \\ {\text{subtract 3 positives}} &{\text{subtract 3 negatives}} \\ {\text{need neutral pairs}} &{\text{need neutral pairs}}\end{array}\nonumber\]
- Propiedad de resta: restar un número es lo mismo que sumar su opuesto.
Glosario
- valor absoluto
- El valor absoluto de un número es su distancia de 0 en la recta numérica. El valor absoluto de un número nn se escribe como |n|.
- enteros
- Los números enteros y sus opuestos se llaman enteros:\(...−3, −2, −1, 0, 1, 2, 3...\)
- opuesto
- Lo opuesto de un número es el número que está a la misma distancia de cero en la recta numérica pero en el lado opuesto de cero: −\(a\) significa lo contrario del número. La notación −\(a\) se lee “lo contrario de”\(a\).


