1.7: Suma y resta fracciones
- Page ID
- 110484
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Sumar o restar fracciones con un denominador común
- Sumar o restar fracciones con diferentes denominadores
- Utilice el orden de las operaciones para simplificar fracciones complejas
- Evaluar expresiones variables con fracciones
Una introducción más completa a los temas tratados en esta sección se puede encontrar en el capítulo Preálgebra, Fracciones.
Sumar o restar fracciones con un denominador común
Cuando multiplicamos fracciones, simplemente multiplicamos los numeradores y multiplicamos los denominadores directamente. Para sumar o restar fracciones, deben tener un denominador común.
Si\(a,b\), y\(c\) son los números donde\(c\neq 0\), entonces
\[\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c} \quad \text{and} \quad \dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a - b}{c}\]
Para sumar o restar fracciones, sumar o restar los numeradores y colocar el resultado sobre el denominador común.
Hacer las actividades de Matemáticas Manipulativas “Adición de Fracción Modelo” y “Resta de Fracción Modelo” te ayudará a desarrollar una mejor comprensión de sumar y restar fracciones.
Encuentra la suma:\(\dfrac{x}{3} + \dfrac{2}{3}\).
- Responder
-
\[\begin{array} {ll} {} &{\dfrac{x}{3} + \dfrac{2}{3}} \\ {\text{Add the numerators and place the sum over the common denominator}} &{\dfrac{x + 2}{3}} \end{array}\]
Encuentra la suma:\(\dfrac{x}{4} + \dfrac{3}{4}\).
- Responder
-
\(\dfrac{x + 3}{4}\)
Encuentra la suma:\(\dfrac{y}{8} + \dfrac{5}{8}\).
- Responder
-
\(\dfrac{y + 5}{8}\)
Encuentra la diferencia:\(-\dfrac{23}{24} - \dfrac{13}{24}\)
- Responder
-
\[\begin{array} {ll} {} &{-\dfrac{23}{24} - \dfrac{13}{24}} \\ {\text{Subtract the numerators and place the }} &{\dfrac{-23 - 13}{24}} \\ {\text{difference over the common denominator}} &{} \\ {\text{Simplify.}} &{\dfrac{-36}{24}} \\ {\text{Simplify. Remember, }-\dfrac{a}{b} = \dfrac{-a}{b}} &{-\dfrac{3}{2}} \end{array}\]
Encuentra la diferencia:\(-\dfrac{19}{28} - \dfrac{7}{28}\)
- Responder
-
\(-\dfrac{26}{28}\)
Encuentra la diferencia:\(-\dfrac{27}{32} - \dfrac{1}{32}\)
- Responder
-
\(-\dfrac{7}{8}\)
Encuentra la diferencia:\(-\dfrac{10}{x} - \dfrac{4}{x}\)
- Responder
-
\[\begin{array} {ll} {} &{-\dfrac{10}{x} - \dfrac{4}{x}} \\ {\text{Subtract the numerators and place the }} &{\dfrac{-14}{x}} \\ {\text{difference over the common denominator}} &{} \\ {\text{Rewrite with the sign in front of the fraction.}} &{-\dfrac{14}{x}} \end{array}\]
Encuentra la diferencia:\(-\dfrac{9}{x} - \dfrac{7}{x}\)
- Responder
-
\(-\dfrac{16}{x}\)
Encuentra la diferencia:\(-\dfrac{17}{a} - \dfrac{5}{a}\)
- Responder
-
\(-\dfrac{22}{a}\)
Simplificar:\(\dfrac{3}{8} + (-\dfrac{5}{8}) - \dfrac{1}{8}\)
- Responder
-
\[\begin{array} {ll} {\text{Add and Subtract fractions — do they have a }} &{\frac{3}{8} + (-\frac{5}{8}) - \frac{1}{8}} \\ {\text{common denominator? Yes.}} &{} \\ {\text{Add and subtract the numerators and place }} &{\frac{3 + (-5) - 1}{8}} \\ {\text{the result over the common denominator.}} &{} \\ {\text{Simplify left to right.}} &{\frac{-2 - 1}{8}} \\ {\text{Simplify.}} &{-\frac{3}{8}} \end{array}\]
Simplificar:\(\dfrac{2}{9} + (-\dfrac{4}{9}) - \dfrac{7}{9}\)
- Responder
-
\(-1\)
Simplificar:\(\dfrac{2}{5} + (-\dfrac{4}{9}) - \dfrac{7}{9}\)
- Responder
-
\(-\dfrac{2}{3}\)
Sumar o restar fracciones con diferentes denominadores
Como hemos visto, para sumar o restar fracciones, sus denominadores deben ser los mismos. El mínimo denominador común (LCD) de dos fracciones es el número más pequeño que se puede utilizar como denominador común de las fracciones. El LCD de las dos fracciones es el múltiplo menos común (LCM) de sus denominadores.
El mínimo común denominador (LCD) de dos fracciones es el mínimo común múltiplo (LCM) de sus denominadores.
Hacer la actividad de Matemáticas Manipulativas “Encontrar el Mínimo Denominador Común” te ayudará a desarrollar una mejor comprensión de la LCD.
Después de encontrar el mínimo denominador común de dos fracciones, convertimos las fracciones a fracciones equivalentes con la LCD. ¡Armando estos pasos nos permite sumar y restar fracciones porque sus denominadores serán los mismos!
Agregar:\(\dfrac{7}{12} + \dfrac{5}{18}\)
- Responder
-



Agregar:\(\dfrac{7}{12} + \dfrac{11}{15}\)
- Responder
-
\(\dfrac{79}{60}\)
Agregar:\(\dfrac{7}{12} + \dfrac{11}{15}\)
- Responder
-
\(\dfrac{103}{60}\)
- ¿Tienen un denominador común?
- Sí—vaya al paso 2.
- No: reescribe cada fracción con la pantalla LCD (mínimo denominador común). Encuentra la pantalla LCD. Cambia cada fracción en una fracción equivalente con la LCD como denominador.
- Sumar o restar las fracciones.
- Simplificar, si es posible.
Al encontrar las fracciones equivalentes necesarias para crear los denominadores comunes, hay una manera rápida de encontrar el número que necesitamos para multiplicar tanto el numerador como el denominador. Este método funciona si encontramos la LCD factorizando en primos.
Observe los factores de la LCD y luego en cada columna por encima de esos factores. Los factores “faltantes” de cada denominador son los números que necesitamos.

En Ejercicio\(\PageIndex{13}\), la LCD, 36, tiene dos factores de 2 y dos factores de 3.
El numerador 12 tiene dos factores de 2 pero sólo uno de 3—así que le falta uno 3—multiplicamos el numerador y el denominador por 3.
Al numerador 18 le falta un factor de 2, por lo que multiplicamos el numerador y el denominador por 2.
Aplicaremos este método a medida que restemos las fracciones en Ejercicio\(\PageIndex{16}\).
Restar:\(\dfrac{7}{15} - \dfrac{19}{24}\)
- Responder
-
¿Las fracciones tienen un denominador común? No, entonces tenemos que encontrar la pantalla LCD.
Encuentra la pantalla LCD. 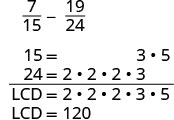
Aviso, 15 está “faltando” tres factores de 2 y 24 está “faltando” el 5 de los factores de la LCD. Entonces multiplicamos 8 en la primera fracción y 5 en la segunda fracción para obtener la LCD. Reescribe como fracciones equivalentes con la pantalla LCD. 
Simplificar. 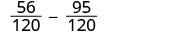
Resta. \(-\dfrac{39}{120}\) Comprueba si se puede simplificar la respuesta. \(-\dfrac{13\cdot3}{40\cdot3}\) Tanto 39 como 120 tienen un factor de 3. Simplificar. \(-\dfrac{13}{40}\) ¡No simplifiques las fracciones equivalentes! Si lo haces, ¡volverás a las fracciones originales y perderás el denominador común!
Restar:\(\dfrac{13}{24} - \dfrac{17}{32}\)
- Responder
-
\(\dfrac{1}{96}\)
Restar:\(\dfrac{7}{15} - \dfrac{19}{24}\)
- Responder
-
\(\dfrac{75}{224}\)
En el siguiente ejemplo, una de las fracciones tiene una variable en su numerador. Observe que hacemos los mismos pasos que cuando ambos numeradores son números.
Agregar:\(\dfrac{3}{5} + \dfrac{x}{8}\)
- Responder
-
Las fracciones tienen diferentes denominadores.
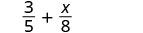
Encuentra la pantalla LCD. 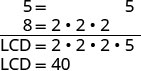
Reescribe como fracciones equivalentes con la pantalla LCD. 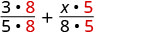
Simplificar. 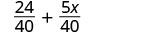
Agregar. 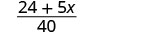
Recuerda, solo podemos agregar términos similares:\(24\) y no\(5x\) son como términos.
Agregar:\(\dfrac{y}{6} + \dfrac{7}{9}\)
- Responder
-
\(\dfrac{3y + 14}{18}\)
Agregar:\(\dfrac{x}{6} + \dfrac{7}{15}\)
- Contestar
-
\(\dfrac{15x + 42}{153}\)
Ahora tenemos las cuatro operaciones para fracciones. La tabla\(\PageIndex{1}\) resume las operaciones de fracciones.
| Multiplicación de Fracciones | División de Fracciones |
| \(\dfrac{a}{b}\cdot \dfrac{c}{d} = \dfrac{ac}{bd}\) Multiplicar los numeradores y multiplicar los denominadores |
\(\dfrac{a}{b}\div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}\) Multiplicar la primera fracción por el recíproco de la segunda. |
| Adición de Fracciones | Resta de Fracciones |
| \(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c}\) Agrega los numeradores y coloca la suma sobre el denominador común. |
\(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c}\) Restar los numeradores y colocar la diferencia sobre el denominador común. |
| Para multiplicar o dividir fracciones, y NO se necesita LCD. Para sumar o restar fracciones, se necesita una pantalla LCD. | |
Simplificar:
- \(\dfrac{5x}{6} - \dfrac{3}{10}\)
- \(\dfrac{5x}{6}\cdot \dfrac{3}{10}\).
- Contestar
-
Primero pregunta: “¿Cuál es la operación?” Una vez que identifiquemos la operación que determinará si necesitamos un denominador común. Recuerden, necesitamos un denominador común para sumar o restar, pero no para multiplicar o dividir.
1. ¿Cuál es la operación? La operación es resta.
\[\begin{array} {ll} {\text{Do the fractions have a common denominator? No.}} &{\frac{5x}{6} - \frac{3}{10}} \\ {\text{Rewrite each fractions as an equivalent fraction with the LCD.}} &{\frac{5x\cdot 5}{6\cdot 5} - \frac{3\cdot3}{10\cdot3}} \\ {} &{\frac{25x}{30} - \frac{9}{30}} \\{\text{Subtract the numerators and place the difference over the}} &{\frac{25x - 9}{30}} \\ {\text{common denominators.}} &{} \\ {\text{Simplify, if possible. There are no common factors.}} &{} \\ {\text{The fraction is simplified.}} &{} \end{array}\]
2. ¿Cuál es la operación? Multiplicación.
\[\begin{array} {ll} {} &{\frac{5x}{6}\cdot \frac{3}{10}} \\ {\text{To multiply fractions, multiply the numerators and multiply}} &{\frac{5x\cdot 3}{6\cdot 10}} \\ {\text{the denominators}} &{} \\{\text{Rewrite, showing common factors.}} &{\frac{\not 5 x\cdot\not3}{2\cdot\not3\cdot2\cdot\not5}} \\ {\text{common denominators.}} &{} \\ {\text{Simplify.}} &{\frac{x}{4}} \end{array}\]
Simplificar:
- \(\dfrac{3a}{4} - \dfrac{8}{9}\)
- \(\dfrac{3a}{4}\cdot\dfrac{8}{9}\)
- Contestar
-
- \(\dfrac{27a - 32}{36}\)
- \(\dfrac{2a}{3}\)
Simplificar:
- \(\dfrac{4k}{5} - \dfrac{1}{6}\)
- \(\dfrac{4k}{5}\cdot\dfrac{1}{6}\)
- Contestar
-
- \(\dfrac{24k - 5}{30}\)
- \(\dfrac{2k}{15}\)
Utilice el orden de operaciones para simplificar fracciones complejas
Hemos visto que una fracción compleja es una fracción en la que el numerat o denominador contiene una fracción. La barra de fracción indica división. Simplificamos la fracción compleja dividiéndola\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\)\(\dfrac{3}{4}\) por\(\dfrac{5}{8}\).
Ahora veremos fracciones complejas donde el numerador o denominador contiene una expresión que se puede simplificar. Entonces primero debemos simplificar completamente el numerador y el denominador por separado usando el orden de las operaciones. Entonces dividimos el numerador por el denominador.
Simplificar:\(\dfrac{(\frac{1}{2})^{2}}{4 + 3^{2}}\)
- Contestar
-



Simplificar:\(\dfrac{(\frac{1}{3})^{2}}{2^{3} + 2}\)
- Contestar
-
\(\dfrac{1}{90}\)
Simplificar:\(\dfrac{1 + 4^{2}}{(\frac{1}{4})^{2}}\)
- Contestar
-
\(272\)
- Simplifica el numerador.
- Simplifica el denominador.
- Divide el numerador por el denominador. Simplificar si es posible.
Simplificar:\(\dfrac{\frac{1}{2} + \frac{2}{3}}{\frac{3}{4} - \frac{1}{6}}\)
- Contestar
-
\[\begin{array} {ll} {} &{\frac{(\frac{1}{2} + \frac{2}{3})}{(\frac{3}{4} - \frac{1}{6})}} \\ {\text{Simplify the numerator (LCD = 6) and simplify the denominator (LCD = 12).}} &{\frac{(\frac{3}{6} + \frac{4}{6})}{(\frac{9}{12} - \frac{2}{12})}} \\ {\text{Simplify.}} &{\frac{(\frac{7}{6})}{(\frac{7}{12})}} \\{\text{Divide the numerator by the denominator.}} &{\frac{7}{6}\div\frac{7}{12}} \\ {\text{Simplify.}} &{\frac{7}{6}\cdot\frac{12}{7}} \\ {\text{Divide out common factors.}} &{\frac{7\cdot6\cdot2}{6\cdot7}} \\ {\text{Simplify.}} &{2} \end{array}\]
Simplificar:\(\dfrac{\frac{1}{3} + \frac{1}{2}}{\frac{3}{4} - \frac{1}{3}}\)
- Contestar
-
\(2\)
Simplificar:\(\dfrac{\frac{2}{3} - \frac{1}{2}}{\frac{1}{4} + \frac{1}{3}}\)
- Contestar
-
\(\dfrac{2}{7}\)
Evaluar expresiones variables con fracciones
Hemos evaluado expresiones antes, pero ahora podemos evaluar expresiones con fracciones. Recuerde, para evaluar una expresión, sustituimos el valor de la variable en la expresión y luego simplificamos.
Evaluar\(x + \dfrac{1}{3}\) cuándo
- \(x = -\dfrac{1}{3}\)
- \(x = -\dfrac{3}{4}\)
- Contestar
-
1. Evaluar\(x + \dfrac{1}{3}\) cuándo\(x = -\dfrac{1}{3}\),\(-\dfrac{1}{3}\) sustituir\(x\) en la expresión.
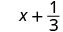
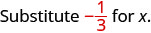
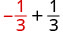
Simplificar. \(0\)
2. Evaluar\(x + \dfrac{1}{3}\) cuándo\(x = -\dfrac{3}{4}\),\(-\dfrac{3}{4}\) sustituir\(x\) en la expresión.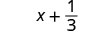

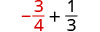
Reescribe como fracciones equivalentes con la pantalla LCD, 12. 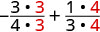
Simplificar. 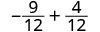
Agregar. \(-\dfrac{5}{12}\)
Evaluar\(x + \dfrac{3}{4}\) cuándo
- \(x = -\dfrac{7}{4}\)
- \(x = -\dfrac{5}{4}\)
- Contestar
-
- \(-1\)
- \(-\dfrac{1}{2}\)
Evaluar\(y + \dfrac{1}{2}\) cuándo
- \(y = \dfrac{2}{3}\)
- \(y = -\dfrac{3}{4}\)
- Contestar
-
- \(\dfrac{7}{6}\)
- \(-\dfrac{1}{12}\)
Evaluar\(-\dfrac{5}{6} - y\) cuándo\(y = -\dfrac{2}{3}\)
- Contestar
-
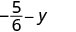
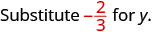
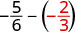
Reescribir como fracciones equivalentes con la pantalla LCD,\(6\). 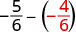
Resta. 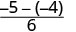
Simplificar. \(-\dfrac{1}{6}\)
Evaluar\(y + \dfrac{1}{2}\) cuándo\(y = \dfrac{2}{3}\)
- Contestar
-
\(-\dfrac{1}{4}\)
Evaluar\(y + \dfrac{1}{2}\) cuándo\(y = \dfrac{2}{3}\)
- Contestar
-
\(-\dfrac{17}{8}\)
Evaluar\(2x^{2}y\) cuándo\(x = \dfrac{1}{4}\) y\(y = -\dfrac{2}{3}\).
- Contestar
-
Sustituir los valores en la expresión.
\(2x^{2}y\) 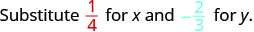
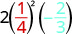
Simplifique primero los exponentes. \(2(\frac{1}{16})(-\frac{2}{3})\) Multiplicar. Dividir los factores comunes. Aviso que escribimos\(16\) como\(2\cdot2\cdot4\) para que sea fácil de quitar \(-\frac{\not2\cdot1\cdot\not2}{\not2\cdot\not2\cdot4\cdot3}\) Simplificar. \(-\frac{1}{12}\)
Evaluar\(3ab^{2}\) cuándo\(a = -\dfrac{2}{3}\) y\(b = -\dfrac{1}{2}\).
- Contestar
-
\(-\dfrac{1}{2}\)
Evaluar\(4c^{3}d\) cuándo\(c = -\dfrac{1}{2}\) y\(d = -\dfrac{4}{3}\).
- Contestar
-
\(\dfrac{2}{3}\)
El siguiente ejemplo solo tendrá variables, no constantes.
Evaluar\(\dfrac{p + q}{r}\) cuándo\(p = -4, q = -2\), y\(r = 8\).
- Contestar
-
Evaluar\(\dfrac{p + q}{r}\) cuándo\(p = -4, q = -2\), y\(r = 8\), sustituimos los valores en la expresión.
\(\dfrac{p + q}{r}\) 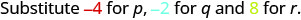
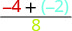
Agregue primero en el numerador. \(\dfrac{-6}{8}\) Simplificar. \(-\dfrac{3}{4}\)
Evaluar\(\dfrac{a+b}{c}\) cuándo\(a = -8, b = -7\), y\(c = 6\).
- Contestar
-
\(-\dfrac{5}{2}\)
Evaluar\(\dfrac{x+y}{z}\) cuándo\(x = 9, y = -18\), y\(z = -6\).
- Contestar
-
\(\dfrac{3}{2}\)
Conceptos clave
- Suma y resta de fracciones: Si\(a, b\), y\(c\) son números donde\(c\neq 0\), entonces
\(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}\) y\(\dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a-b}{c}\)
Para sumar o restar fracciones, sumar o restar los numeradores y colocar el resultado sobre el denominador común.
- Estrategia para sumar o restar fracciones
- ¿Tienen un denominador común?
Sí, vaya al paso 2.
No: reescribe cada fracción con la pantalla LCD (mínimo denominador común). Encuentra la pantalla LCD. Cambia cada fracción en una fracción equivalente con la LCD como denominador. - Sumar o restar las fracciones.
- Simplificar, si es posible. Para multiplicar o dividir fracciones, NO SE necesita una pantalla LCD. Para sumar o restar fracciones, se necesita una pantalla LCD.
- ¿Tienen un denominador común?
- Simplificar fracciones complejas
- Simplifica el numerador.
- Simplifica el denominador.
- Divide el numerador por el denominador. Simplificar si es posible.


