1.10: Propiedades de los números reales
- Page ID
- 110459
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Utilizar las propiedades conmutativas y asociativas
- Utilizar la identidad y las propiedades inversas de suma y multiplicación
- Usa las propiedades de cero
- Simplificar expresiones usando la propiedad distributiva
Una introducción más completa a los temas tratados en esta sección se puede encontrar en el capítulo de Preálgebra, Las propiedades de los números reales.
Utilizar las propiedades conmutativas y asociativas
Piensa en sumar dos números, digamos 5 y 3. El orden que los agregamos no afecta el resultado, ¿verdad?
\[\begin{array} { cc } { 5 + 3 } & { 3 + 5 } \\ { 8 } & { 8 } \\ { 5 + 3 = } & { 3 + 5 } \end{array}\]
Los resultados son los mismos.
Como podemos ver, ¡el orden en que agreguemos no importa!
¿Qué pasa con multiplicar 5 y 3?
\[\begin{array} { c c } { 5 \cdot 3 } & { 3 \cdot 5 } \\ { 15 } & { 15 } \\ { 5 \cdot 3=} &{3 \cdot 5 } \end{array}\]
De nuevo, ¡los resultados son los mismos!
¡El orden en que nos multiplicamos no importa!
Estos ejemplos ilustran la propiedad conmutativa. Al sumar o multiplicar, cambiar el orden da el mismo resultado.
\[\begin{array} { l l } { \textbf { of Addition } } & { \text { If } a , b \text { are real numbers, then } \quad a + b = b + a } \\ { \textbf { of Multiplication } } & { \text { If } a , b \text { are real numbers, then } \quad a \cdot b = b \cdot a } \end{array}\]
Al sumar o multiplicar, cambiar el orden da el mismo resultado.
La propiedad conmutativa tiene que ver con el orden. Si cambia el orden de los números al sumar o multiplicar, el resultado es el mismo.
¿Y qué pasa con la resta? ¿Importa el orden cuando restamos números? ¿7−3 da el mismo resultado que 3−7?
\[\begin{array} { c c } { 7 - 3 } & { 3 - 7 } \\ { 4 } & { - 4 } \end{array}\]
\[\begin{aligned} 4 & \neq - 4 \\ 7 - 3 & \neq 3 - 7 \end{aligned}\]
Los resultados no son los mismos.
Dado que cambiar el orden de la resta no dio el mismo resultado, sabemos que la resta no es conmutativa.
Veamos qué pasa cuando dividimos dos números. ¿Es la división conmutativa?
\[\begin{array} { cc} { 12 \div 4 } & { 4 \div 12 } \\ { \frac { 12 } { 4 } } & { \frac { 4 } { 12 } } \\ { 3 } & { \frac { 1 } { 3 } } \end{array}\]
\[\begin{aligned} 3 \neq & \frac { 1 } { 3 } \\ 12 \div 4 & \neq 4 \div 12 \end{aligned}\]
Los resultados no son los mismos.
Dado que cambiar el orden de la división no dio el mismo resultado, la división no es conmutativa. ¡Las propiedades conmutativas solo se aplican a la suma y multiplicación!
- La suma y la multiplicación son conmutativas.
- La resta y la división no son conmutativas.
Si te pidieran que simplificaras esta expresión, ¿cómo la harías y cuál sería tu respuesta?
\[7 + 8 + 2\]
Algunas personas pensarían que\(7+8\) es 15 y luego\(15+2\) es 17. Otros podrían comenzar con\(8+2\) hace 10 y luego\(7+10\) hace 17.
De cualquier manera da el mismo resultado. Recuerde, usamos paréntesis como símbolos de agrupación para indicar qué operación se debe hacer primero.
\[\begin{array} { ll } { \text{ Add } 7 + 8 . } & { ( 7 + 8 ) + 2 } \\ { \text { Add. } } & { 15 + 2 } \\ { \text { Add. } } & { 17 } \\ \\ { } & { 7 + ( 8 + 2 ) } \\ { \text { Add } 8 + 2 . } & { 7 + 10 } \\ { \text { Add. } } & { 77 } \\\\ { ( 7 + 8 ) + 2 = 7 + ( 8 + 2 ) } \end{array}\]
Al sumar tres números, cambiar la agrupación de los números da el mismo resultado.
Esto también es cierto para la multiplicación.
\[\begin{array} { ll } { } & { (5\cdot \frac{1}{3})\cdot 3 } \\ { \text { Multiply. } 5\cdot \frac{1}{3} } & { \frac{5}{3}\cdot 3 } \\ { \text { Multiply. } } & { 5 } \\ \\ { } & { 5\cdot (\frac{1}{3}\cdot 3) } \\ { \text { Multiply. } \frac{1}{3}\cdot 3 } & { 5\cdot 1 } \\ { \text { Multiply. } } & { 5 } \\ \\ { (5\cdot \frac{1}{3})\cdot 3 = 5\cdot (\frac{1}{3}\cdot 3) } \end{array}\]
Al multiplicar tres números, cambiar la agrupación de los números da el mismo resultado.
Probablemente lo sepas, pero la terminología puede ser nueva para ti. Estos ejemplos ilustran la propiedad asociativa.
\[\begin{array} { l l } { \textbf { of Addition } } & { \text { If } a , b , c \text { are real numbers, then } ( a + b ) + c = a + ( b + c ) } \\ { \textbf { of Multiplication } } & { \text { If } a , b , c \text { are real numbers, then } ( a \cdot b ) \cdot c = a \cdot ( b \cdot c ) } \end{array}\]
Al sumar o multiplicar, cambiar la agrupación da el mismo resultado.
Pensemos de nuevo en multiplicar\(5\cdot \frac{1}{3}\cdot 3\). Obtuvimos el mismo resultado en ambos sentidos, pero ¿cuál fue más fácil? Multiplicando\(\frac{1}{3}\) y 3 primero, como se muestra arriba en el lado derecho, elimina la fracción en el primer paso. ¡Usar la propiedad asociativa puede facilitar las matemáticas!
La propiedad asociativa tiene que ver con la agrupación. Si cambiamos la forma en que se agrupan los números, el resultado será el mismo. Observe que son los mismos tres números en el mismo orden, la única diferencia es la agrupación.
Vimos que la resta y la división no eran conmutativas. Tampoco son asociativas.
A la hora de simplificar una expresión, siempre es buena idea planificar cuáles serán los pasos. Para combinar términos similares en el siguiente ejemplo, usaremos la propiedad conmutativa de suma para escribir los términos similares juntos.
Simplificar:\(18p+6q+15p+5q\).
- Responder
-
\[\begin{array} { l l} {} &{18p+6q+15p+5q}\\ \\{ \text { Use the commutative property of addition } } &{} \\ { \text {to re-order so that like terms are together.} } &{18p+15p+ 6q+5q} \\ \\ {\text{Add like terms.}} &{33p + 11q} \end{array}\]
Simplificar:\(23r+14s+9r+15s\).
- Responder
-
\(32r+29s\)
Simplificar:\(37m+21n+4m−15n\).
- Responder
-
\(41m+6n\)
Cuando tenemos que simplificar la expresión algebraica s, a menudo podemos facilitar el trabajo aplicando primero la propiedad conmutativa o asociativa, en lugar de seguir automáticamente el orden de las operaciones. Al sumar o restar fracciones, combine primero aquellas que tengan un denominador común.
Simplificar:\((\frac{5}{13} + \frac{3}{4}) + \frac{1}{4}\)
- Responder
-
\[\begin{array} { l l } {} &{(\frac{5}{13} + \frac{3}{4}) + \frac{1}{4}} \\{ \text { Notice that the last } 2 \text { terms have a } } \\ { \text { common denominator, so change the } } &{\frac { 5 } { 13 } + \left( \frac { 3 } { 4 } + \frac { 1 } { 4 } \right)}\\ { \text { grouping. } } &{}\\ \\ {\text{Add in parentheses first.}} &{\frac{5}{13} + (\frac{4}{4})} \\ \\ {\text{Simplify the fraction.}} &{\frac{5}{13} + 1} \\ \\ {\text{Add.}} &{1\frac{5}{13}} \\ \\ {\text{Convert to an improper fraction.}} &{\frac{18}{13}} \end{array}\]
Simplificar:\((\frac{7}{15} + \frac{5}{8}) + \frac{3}{8}\)
- Responder
-
\(1\frac{7}{15}\)
Simplificar:\((\frac{2}{9} + \frac{7}{12}) + \frac{5}{12}\)
- Responder
-
\(1\frac{2}{9}\)
Utilice la propiedad asociativa para simplificar\(6(3x)\).
- Responder
-
Utilice la propiedad asociativa de multiplicación,\((a\cdot b)\cdot c=a\cdot (b\cdot c)\), para cambiar la agrupación.
\[\begin{array} { ll } {} &{ 6 ( 3 x ) } \\ { \text { Change the grouping. } } &{(6\cdot 3)x} \\ { \text { Multiply in the parentheses. } } &{18} \end{array}\]
Observe que podemos multiplicar\(6\cdot 3\) pero no podríamos multiplicar\(3x\) sin tener un valor para\(x\).
Utilice la propiedad asociativa para simplificar\(8(4x)\).
- Responder
-
\(32x\)
Utilice la propiedad asociativa para simplificar\(-9(7y)\).
- Responder
-
\(-63y\)
Utilizar la identidad y las propiedades inversas de la suma y la multiplicación
¿Qué sucede cuando sumamos 0 a algún número? Agregar 0 no cambia el valor. Por esta razón, llamamos a 0 la identidad aditiva.
Por ejemplo,
\[\begin{array} { c c c } { 13 + 0 } & { - 14 + 0 } & { 0 + ( - 8 ) } \\ { 13 } & { - 14 } & { - 8 } \end{array}\]
Estos ejemplos ilustran la Identidad Propiedad de Adición que establece que para cualquier número real\(a\),\(a+0=a\) y\(0+a=a\).
¿Qué pasa cuando multiplicamos cualquier número por uno? Multiplicar por 1 no cambia el valor. Entonces llamamos a 1 la identidad multiplicativa.
Por ejemplo,\[\begin{array} { r r r } { 43 \cdot 1 } & { - 27 \cdot 1 } & { 1 \cdot \frac { 3 } { 5 } } \\ { 43 } & { - 27 } & { \frac { 3 } { 5 } } \end{array}\]
Estos ejemplos ilustran la Identidad Propiedad de la Multiplicación que establece que para cualquier número real\(a\),\(a\cdot 1=a\) y\(1\cdot a=a\).
Resumimos las Propiedades de Identidad a continuación.
\[\begin{array} { l l} { \textbf {of addition}\text{ For any real number } a : } &{ a + 0 = a \quad 0 + a = a } \\ { \textbf{0} \text { is the}\textbf{ additive identity } } \\ {\textbf {of multiplication}\text{ For any real number } a : } &{ a \cdot 1 = a \quad 1 \cdot a = a } \\ { \textbf{1}\text{ is the}\textbf{ multiplicative identity } } \end{array}\]

¡Observe que en cada caso, el número faltante era el opuesto al número!
Nosotros llamamos\(−a\). la inversa aditiva de a. Lo contrario de un número es su inverso aditivo. Un número y su opuesto se suman a cero, que es la identidad aditiva. Esto lleva a la Propiedad Inversa de Adición que establece para cualquier número real\(a, a+(−a)=0\). Recuerda, un número y su opuesto se suman a cero.
¿Qué número multiplicado por\(\frac{2}{3}\) da la identidad multiplicativa, 1? En otras palabras, ¿\(\frac{2}{3}\)veces qué resulta en 1?

¿Qué número multiplicado por 2 da la identidad multiplicativa, 1? En otras palabras 2 veces lo que resulta en 1?

¡Observe que en cada caso, el número faltante era el recíproco del número!
Llamamos a\(\frac{1}{a}\) la inversa multiplicativa de a. El recíproco del número aa es su inverso multiplicativo. Un número y su recíproco se multiplican a uno, que es la identidad multiplicativa. Esto lleva a la Propiedad Inversa de la Multiplicación que establece eso para cualquier número real\(a, a\neq 0, a\cdot \frac{1}{a}=1\).
Aquí declararemos formalmente las propiedades inversas:
\[\begin{array} { l l l } { \textbf { of addition } } &{ \text { For any real number } a,} &{a + (-a) = 0}\\{} &{-a \text{. is the}\textbf{ additive inverse} \text{ of }a} &{}\\ {} &{ \text { A number and its opposite add to zero. } }&{}\\ \\{ \textbf { of multiplication } } &{ \text { For any real number } a, a\neq 0} &{a\cdot \frac{1}{a} = 1}\\{} &{\frac{1}{a} \text{. is the}\textbf{ multiplicative inverse} \text{ of }a} &{}\\ {} &{ \text { A number and its reciprocal multiply to zero. } }&{} \end{array}\]
Encuentra la inversa aditiva de
- \(\frac{5}{8}\)
- \(0.6\)
- \(-8\)
- \(-\frac{4}{3}\)
- Responder
-
Para encontrar el inverso aditivo, encontramos lo contrario.
- La inversa aditiva de\(\frac{5}{8}\) es lo opuesto a\(\frac{5}{8}\). La inversa aditiva de\(\frac{5}{8}\) es\(-\frac{5}{8}\)
- La inversa aditiva de\(0.6\) es lo opuesto a\(0.6\). La inversa aditiva de\(0.6\) es\(-0.6\).
- La inversa aditiva de\(-8\) es lo opuesto a\(-8\). Escribimos lo contrario de\(-8\) as\(-(-8)\), y luego lo simplificamos a\(8\). Por lo tanto, la inversa aditiva de\(-8\) es\(8\).
- La inversa aditiva de\(-\frac{4}{3}\) es lo opuesto a\(-\frac{4}{3}\). Escribimos esto como\(-(-\frac{4}{3})\), y luego simplificamos a\(\frac{4}{3}\). Así, la inversa aditiva de\(-\frac{4}{3}\) es\(\frac{4}{3}\).
Encuentra la inversa aditiva de
- \(\frac{7}{9}\)
- \(1.2\)
- \(-14\)
- \(-\frac{9}{4}\)
- Responder
-
- \(-\frac{7}{9}\)
- \(-1.2\)
- \(14\)
- \(\frac{9}{4}\)
Encuentra la inversa aditiva de
- \(\frac{7}{13}\)
- \(8.4\)
- \(-46\)
- \(-\frac{5}{2}\)
- Responder
-
- \(-\frac{7}{13}\)
- \(-8.4\)
- \(46\)
- \(\frac{5}{2}\)
Encuentra el inverso multiplicativo de
- \(9\)
- \(-\frac{1}{9}\)
- \(0.9\)
- Responder
-
Para encontrar el inverso multiplicativo, encontramos el recíproco.
- El inverso multiplicativo de\(9\) es el recíproco de\(9\), que es\(\frac{1}{9}\). Por lo tanto, la inversa multiplicativa de\(9\) es\(\frac{1}{9}\).
- El inverso multiplicativo de\(-\frac{1}{9}\) es el recíproco de\(-\frac{1}{9}\), que es\(−9\). Así, la inversa multiplicativa de\(-\frac{1}{9}\) es\(-9\).
- Para encontrar el inverso multiplicativo de\(0.9\), primero convertimos\(0.9\) a una fracción,\(\frac{9}{10}\). Entonces encontramos el recíproco de la fracción. El recíproco de\(\frac{9}{10}\) es\(\frac{10}{9}\). Entonces el inverso multiplicativo de\(0.9\) es\(\frac{10}{9}\).
Encuentra el inverso multiplicativo de
- \(4\)
- \(-\frac{1}{7}\)
- \(0.3\)
- Responder
-
- \(\frac{1}{4}\)
- \(-7\)
- \(\frac{10}{3}\)
Encuentra el inverso multiplicativo de
- \(18\)
- \(-\frac{4}{5}\)
- \(0.6\)
- Responder
-
- \(\frac{1}{18}\)
- \(-\frac{5}{4}\)
- \(\frac{5}{3}\)
Usa las Propiedades de Zero
La propiedad de identidad de suma dice que cuando agregamos 0 a cualquier número, el resultado es ese mismo número. ¿Qué sucede cuando multiplicamos un número por 0? Multiplicar por 0 hace que el producto sea igual a cero.
Para cualquier número real a.
\[a \cdot 0 = 0 \quad 0 \cdot a = 0\]
El producto de cualquier número real y 0 es 0.
¿Qué pasa con la división que involucra cero? ¿Qué es\(0\div 3\)? Piensa en un ejemplo real: Si no hay galletas en el tarro de galletas y 3 personas están para compartirlas, ¿cuántas galletas obtiene cada persona? No hay cookies para compartir, por lo que cada persona obtiene 0 cookies. Entonces,
\[0\div 3 = 0\]
Podemos verificar la división con el hecho de multiplicación relacionado.
\[12 \div 6 = 2 \text { because } 2 \cdot 6 = 12\]
Entonces sabemos\(0\div 3=0\) porque\(0\cdot 3=0\).
Para cualquier número real a, excepto\(0, \frac{0}{a}=0\) y\(0\div a=0\).
Cero dividido por cualquier número real excepto cero es cero.
Ahora piensa en dividir por cero. ¿Cuál es el resultado de dividir 4 por 0? Piense en el hecho de multiplicación relacionado:\(4\div 0=?\) medios\(?\cdot 0=4\). ¿Hay un número que multiplicado por 0 da 4? Dado que cualquier número real multiplicado por 0 da 0, no hay un número real que pueda multiplicarse por 0 para obtener 4.
Concluimos que no hay respuesta a\(4\div 0\) y así decimos que la división por 0 es indefinida.
Para cualquier número real a, excepto\(0, \frac{a}{0}\) y\(a\div 0\) son indefinidos.
La división por cero no está definida.
Resumimos las propiedades de cero abajo.
Multiplicación por Cero: Para cualquier número real a,
\[a \cdot 0 = 0 \quad 0 \cdot a = 0 \quad \text { The product of any number and } 0 \text { is } 0\]
División de Cero, División por Cero: Para cualquier número real\(a, a\neq 0\)
\[\begin{array} { l l } { \frac { 0 } { a } = 0 } & { \text { Zero divided by any real number, except itself is zero. } } \\ { \frac { a } { 0 } \text { is undefined } } & { \text { Division by zero is undefined. } } \end{array}\]
Simplificar:
- \(-8\cdot 0\)
- \(\frac{0}{-2}\)
- \(\frac{-32}{0}\)
- Responder
-
- \[\begin{array} { cc } { } &{-8\cdot 0}\\{\text{The product of any real number and 0 is 0}} &{0}\end{array}\]
- \[\begin{array} { ll } { } &{\frac{0}{-2}}\\{\text{Zero divided by any real number, except}} &{} \\ {\text{itself, is 0}} &{0}\end{array}\]
- \[\begin{array} { ll } { } &{\frac{-32}{0}}\\ {\text{Division by 0 is undefined.}} &{\text{undefined}} \end{array}\]
Simplificar:
- \(-14\cdot 0\)
- \(\frac{0}{-6}\)
- \(\frac{-2}{0}\)
- Responder
-
- \(0\)
- \(0\)
- undefined
Simplificar:
- \(0(-17)\)
- \(\frac{0}{-10}\)
- \(\frac{-5}{0}\)
- Responder
-
- \(0\)
- \(0\)
- undefined
Ahora vamos a practicar el uso de las propiedades de identidades, inversos y cero para simplificar las expresiones.
Simplificar:
- \(\frac{0}{n + 5}\), donde\(n\neq −5\)
- \(\frac{10 - 3p}{0}\)donde\(10 - 3p \neq 0\)
- Responder
-
- \[\begin{array} { ll } { } &{\frac{0}{n + 5}}\\ {\text { Zero divided by any real number except }} &{0} \\ { \text { itself is } 0.} &{} \end{array}\]
- \[\begin{array} { ll } { } &{\frac{10 - 3p}{0}}\\ {\text { Division by 0 is undefined }} &{\text{undefined}} \end{array}\]
Simplificar:\(−84n+(−73n)+84n\).
- Responder
-
\[\begin{array} { l l } { } &{−84n+(−73n)+84n} \\ { \text { Notice that the first and third terms are } } &{}\\ { \text { opposites; use the commutative property of } } &{- 84 n + 84 n + ( - 73 n ) } \\ { \text { addition to re-order the terms. } } &{} \\ \\ { \text { Add left to right. } } &{0 + (-73)}\\ \\{ \text { Add. } } &{-73n} \end{array}\]
Simplificar:\(−27a+(−48a)+27a\).
- Responder
-
\(−48a\)
Simplificar:\(39x+(−92x)+(−39x)\).
- Responder
-
\(−92x\)
Ahora veremos cómo es útil reconocer los recíprocos. Antes de multiplicar de izquierda a derecha, busque reciprocales—su producto es 1.
Simplificar:\(\frac{7}{15}\cdot\frac{8}{23}\cdot\frac{15}{7}\)
- Responder
-
\[\begin{array} { l l } { } &{\frac{7}{15}\cdot\frac{8}{23}\cdot\frac{15}{7}} \\ { \text { Notice that the first and third terms are } } &{}\\ { \text { reciprocals, so use the commutative } } &{\frac{7}{15}\cdot\frac{15}{7}\cdot\frac{8}{23}} \\ { \text { property of multiplication to re-order the } } &{} \\ { \text { factors. } } &{}\\ \\{ \text { Multiply left to right. } } &{1\cdot\frac{8}{23}} \\\\{\text{Multiply.}} &{\frac{8}{23}}\end{array}\]
Simplificar:\(\frac{9}{16}\cdot\frac{5}{49}\cdot\frac{16}{9}\)
- Responder
-
\(\frac{5}{49}\)
Simplificar:\(\frac{6}{17}\cdot\frac{11}{25}\cdot\frac{17}{6}\)
- Responder
-
\(\frac{11}{25}\)
Simplificar:
- \(\frac{0}{m + 7}\), donde\(m \neq -7\)
- \(\frac{18 - 6c}{0}\), donde\(18 - 6c \neq 0\)
- Responder
-
- 0
- undefined
Simplificar:
- \(\frac{0}{d - 4}\), donde\(d \neq 4\)
- \(\frac{15 - 4q}{0}\), donde\(15 - 4q \neq 0\)
- Responder
-
- 0
- undefined
Simplificar:\(\frac{3}{4}\cdot\frac{4}{3}(6x + 12)\)
- Responder
-
\[\begin{array} { l l } { } &{\frac{3}{4}\cdot\frac{4}{3}(6x + 12)} \\ { \text { There is nothing to do in the parentheses, } } &{}\\ { \text { so multiply the two fractions first—notice, } } &{1(6x + 12)} \\ { \text { they are reciprocals. } } &{} \\ \\{ \text { Simplify by recognizing the multiplicative } } &{} \\{\text{ identity.}} &{6x + 12} \end{array}\]
Simplificar:\(\frac{2}{5}\cdot\frac{5}{2}(20y + 50)\)
- Responder
-
\(20y + 50\)
Simplificar:\(\frac{3}{8}\cdot\frac{8}{3}(12z + 16)\)
- Responder
-
\(12z + 16\)
Simplificar expresiones mediante la propiedad distributiva
Supongamos que tres amigos van al cine. Cada uno necesita $9.25, es decir, 9 dólares y 1 cuarto, para pagar sus boletos. ¿Cuánto dinero necesitan todos juntos?
Se puede pensar en los dólares por separado de los trimestres. Necesitan 3 veces $9 entonces $27, y 3 veces 1 trimestre, entonces 75 centavos. En total, necesitan 27.75 dólares. Si piensas en hacer las matemáticas de esta manera, estás usando la propiedad distributiva.
\[\begin{array} { rr } {\text { If } a , b , c \text { are real numbers, then }} &{a ( b + c ) = a b + a c} \\ \\{ \text { Also,} } &{( b + c ) a = b a + c a} \\ {} &{a ( b - c ) = a b - a c } &{} \\{} &{( b - c ) a = b a - c a } \end{array}\]
De vuelta a nuestros amigos en el cine, podríamos encontrar la cantidad total de dinero que necesitan así:
\[\begin{array} { c } { 3 ( 9.25 ) } \\ { 3 ( 9 + 0.25 ) } \\ { 3 ( 9 ) + 3 ( 0.25 ) } \\ { 27 + 0.75 } \\ \\ { 27.75 } \end{array}\]
En álgebra, utilizamos la propiedad distributiva para eliminar paréntesis a medida que simplificamos las expresiones.
Por ejemplo, si se nos pide simplificar la expresión\(3(x+4)\), el orden de las operaciones dice trabajar primero entre paréntesis. Pero no podemos agregar x y 4, ya que no son como términos. Entonces usamos la propiedad distributiva, como se muestra en Ejercicio\(\PageIndex{31}\).
Simplificar:\(3(x+4)\).
- Responder
-
\[\begin{array} { l l } { } & { 3 ( x + 4 ) } \\ { \text { Distribute. } } & { 3 \cdot x + 3 \cdot 4 } \\ { \text { Multiply. } } & { 3 x + 12 } \end{array}\]
Simplificar:\(4(x+2)\).
- Responder
-
\(4x + 8\)
Simplificar:\(6(x+7)\).
- Responder
-
\(6x + 42\)
A algunos estudiantes les resulta útil dibujar flechas para recordarles cómo usar la propiedad distributiva. Entonces el primer paso en Ejercicio se\(\PageIndex{31}\) vería así:
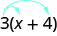
Simplificar:\(8(\frac{3}{8}x+\frac{1}{4})\).
- Responder
-
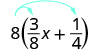
Distribuir. 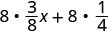
Multiplicar. 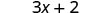
Simplificar:\(6(\frac{5}{6}y+\frac{1}{2})\).
- Responder
-
\(5y + 3\)
Simplificar:\(12(\frac{1}{3}n+\frac{3}{4})\).
- Responder
-
\(4n + 9\)
El uso de la propiedad distributiva como se muestra en Ejercicio\(\PageIndex{37}\) será muy útil cuando resolvamos aplicaciones de dinero en capítulos posteriores.
Simplificar:\(100(0.3+0.25q)\).
- Responder
-
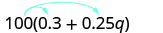
Distribuir. 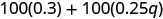
Multiplicar. 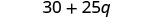
Simplificar:\(100(0.7+0.15p)\).
- Responder
-
\(70 + 15p\)
Simplificar:\(100(0.04+0.35d)\).
- Responder
-
\(4 + 35d\)
Cuando distribuimos un número negativo, ¡debemos tener mucho cuidado para que las señales sean correctas!
Simplificar:\(−2(4y+1)\).
- Responder
-
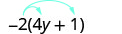
Distribuir. 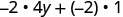
Multiplicar. 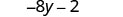
Simplificar:\(−3(6m+5)\).
- Responder
-
\(−18m-15)\)
Simplificar:\(−6(8n+11)\).
- Responder
-
\(−48n- 66)\)
Simplificar:\(−11(4-3a)\).
- Responder
-
Distribuir. 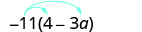
Multiplicar. 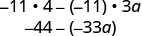
Simplificar. 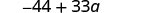
Observe que también podría escribir el resultado como\(33a−44\). ¿Sabes por qué?
Simplificar:\(−5(2-3a)\).
- Responder
-
\(10+ 15a\)
Simplificar:\(−7(8-15y)\).
- Responder
-
\(-56 + 105y\)
El ejercicio\(\PageIndex{46}\) mostrará cómo usar la propiedad distributiva para encontrar lo contrario de una expresión.
Simplificar:\(−(y+5)\).
- Responder
-
\[\begin{array} { ll } {} &{-(y + 5)} \\ \\{ \text {Multiplying by -1 results in the opposite.} } &{-1( y + 5 )} \\ \\ {\text{Distribute.}} &{-1\cdot y + (-1)\cdot 5}\\ \\{\text{Simplify.}} &{-y + (-5)} \\ \\ {} &{-y - 5} \end{array}\]
Simplificar:\(−(z-11)\).
- Responder
-
\(-z + 11\)
Simplificar:\(−(x -4)\).
- Responder
-
\(-x + 4\)
Habrá momentos en los que necesitaremos usar la propiedad distributiva como parte del orden de operaciones. Empieza por mirar los paréntesis. Si no se puede simplificar la expresión dentro de los paréntesis, el siguiente paso sería multiplicar usando la propiedad distributiva, que elimina los paréntesis. Los siguientes dos ejemplos ilustrarán esto.
Simplificar:\(8−2(x + 3)\).
Asegúrese de seguir el orden de las operaciones. La multiplicación viene antes de la resta, por lo que distribuiremos primero los 2 y luego restaremos.
- Responder
-
\[\begin{array} { ll } {} &{8−2(x + 3)} \\ \\{ \text {Distribute.} } &{8−2\cdot x -2\cdot 3} \\ \\ {\text{Multiply.}} &{8 - 2x - 6}\\ \\{\text{Combine like terms.}} &{-2x + 2} \end{array}\]
Simplificar:\(9−3(x + 2)\).
- Responder
-
\(3 - 3x\)
Simplificar:\(7x−5(x + 4)\).
- Responder
-
\(2x - 20\)
Simplificar:\(4(x - 8)−(x + 3)\).
- Responder
-
\[\begin{array} { ll } {} &{4(x - 8)−(x + 3)} \\ \\{ \text {Distribute.} } &{4x - 32 - x - 3} \\ \\{\text{Combine like terms.}} &{3x - 35} \end{array}\]
Simplificar:\(6(x - 9)−(x + 12)\).
- Responder
-
\(5x - 66\)
Simplificar:\(8(x - 1)-(x + 5)\).
- Responder
-
\(7x - 13\)
Todas las propiedades de los números reales que hemos utilizado en este capítulo se resumen en Tabla\(\PageIndex{1}\).
| Propiedad conmutativa | |
| de suma Si a, b son números reales, entonces de multiplicación Si a, b son números reales, entonces |
\(a+b=b+a\) \(a\cdot b=b\cdot a\) |
| Propiedad asociativa | |
| de suma Si a, b, c son números reales, entonces de multiplicación Si a, b, c son números reales, entonces |
\((a+b)+c=a+(b+c)\) \((a\cdot b)\cdot c=a\cdot (b\cdot c)\) |
| Propiedad distributiva | |
| Si a, b, c son números reales, entonces | \(a(b+c)=ab+ac\) |
| Propiedad de Identidad | |
|
de adición Para cualquier número real a: de multiplicación Para cualquier número real a: |
\(a+0=a\) \(0+a=a\) \(1·a=a\) |
| Inverse (propiedad) | |
| de suma Para cualquier número real a, \(−a\) es el inverso aditivo de a de multiplicación Para cualquier número real\(a,a\neq 0\) \(\frac{1}{a}\) es el inverso multiplicativo de a |
\(a+(−a)=0\) \(a\cdot\frac{1}{a}=1\) |
| Inmuebles de Zero | |
|
Para cualquier número real a, Para cualquier número real\(a,a\neq 0\) |
\(a\cdot 0=0\) \(0\cdot a=0\) \(\frac{0}{a} = 0\) |
Conceptos clave
- Propiedad conmutativa de
- Suma: Si a, b son números reales, entonces\(a+b=b+a\).
- Multiplicación: Si a, b son números reales, entonces\(a\cdot b=b\cdot a\). Al sumar o multiplicar, cambiar el orden da el mismo resultado.
- Propiedad asociativa de
- Suma: Si a, b, c son números reales, entonces\((a+b)+c=a+(b+c)\).
- Multiplicación: Si a, b, c son números reales, entonces\((a\cdot b)\cdot c=a\cdot (b\cdot c)\).
Al sumar o multiplicar, cambiar la agrupación da el mismo resultado.
- Propiedad distributiva: Si a, b, c son números reales, entonces
- \(a(b+c)=ab+ac\)
- \((b+c)a=ba+ca\)
- \(a(b-c)=ab-ac\)
- \((b+c)a=ba-ca\)
- Propiedad Identidad
- de Adición: Para cualquier número real a:\(a+0=a\)
0 es la identidad aditiva - de Multiplicación: Para cualquier número real a:\(a\cdot 1=a \quad 1·a=a\)
1 1 es la identidad multiplicativa
- de Adición: Para cualquier número real a:\(a+0=a\)
- Inverse (propiedad)
- de Adición: Para cualquier número real\(a, a+(−a)=0\). Un número y su opuesto se suman a cero. \(−a\)es la inversa aditiva de a.
- de Multiplicación: Para cualquier número real\(a,(a\neq 0)a\cdot\frac{1}{a}=1\). Un número y su recíproco se multiplican a uno. \(\frac{1}{a}\)es la inversa multiplicativa de a.
- Inmuebles de Zero
- Para cualquier número real a,
\(a\cdot 0=0 \quad 0·a=0\) — El producto de cualquier número real y 0 es 0. - \(\frac{0}{a}=0\)para\(a\neq 0\) — Cero dividido por cualquier número real excepto cero es cero.
- \(\frac{a}{0}\)es undefined — División por cero es indefinida.
- Para cualquier número real a,


