9.4: Multiplicar raíces cuadradas
- Page ID
- 110163
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Multiplicar raíces cuadradas
- Usar multiplicación polinomial para multiplicar raíces cuadradas
Antes de comenzar, toma este cuestionario de preparación.
- Simplificar: (3u) (8v).
Si te perdiste este problema, revisa el Ejemplo 6.2.31. - Simplificar: 6 (12−7n).
Si te perdiste este problema, revisa el Ejemplo 6.3.1. - Simplificar: (2+a) (4−a).
Si te perdiste este problema, revisa el Ejemplo 6.3.34.
Multiplicar raíces cuadradas
Hemos utilizado la Propiedad del Producto de Raíces Cuadradas para simplificar las raíces cuadradas eliminando los factores cuadrados perfectos. El Producto Propiedad de Raíces Cuadradas dice
\[\sqrt{ab}=\sqrt{a}·\sqrt{b} \nonumber\]
Podemos utilizar la Propiedad del Producto de Raíces Cuadradas 'a la reversa' para multiplicar raíces cuadradas.
\[\sqrt{a}·\sqrt{b}=\sqrt{ab} \nonumber\]
Recuerde, suponemos que todas las variables son mayores o iguales a cero.
Reescribiremos la Propiedad del Producto de Raíces Cuadradas para que veamos ambos caminos juntos.
Si a, b son números reales no negativos, entonces
\(\sqrt{ab}=\sqrt{a}·\sqrt{b}\)y\(\sqrt{a}·\sqrt{b}=\sqrt{ab}\).
Así podemos multiplicar\(\sqrt{3}·\sqrt{5}\) in this way:
\[\begin{array}{l} {\sqrt{3}·\sqrt{5}}\\ {\sqrt{3·5}}\\ {\sqrt{15}}\\ \nonumber \end{array}\]
A veces el producto nos da un cuadrado perfecto:
\[\begin{array}{l} {\sqrt{2}·\sqrt{8}}\\ {\sqrt{2·8}}\\ {\sqrt{16}}\\ {4}\\ \nonumber \end{array}\]
Incluso cuando el producto no es un cuadrado perfecto, debemos buscar factores cuadrados perfectos y simplificar el radical siempre que sea posible.
Multiplicar radicales con coeficientes es muy parecido a multiplicar variables con coeficientes. Para multiplicar 4x·3y multiplicamos los coeficientes juntos y luego las variables. El resultado es 12xy. Ten esto en cuenta al hacer estos ejemplos.
Simplificar:
- \(\sqrt{2}·\sqrt{6}\)
- \((4\sqrt{3})(2\sqrt{12})\).
- Contestar
-
1. \(\sqrt{2}·\sqrt{6}\) Multiplicar usando la Propiedad del Producto. \(\sqrt{12}\) Simplifica lo radical. \(\sqrt{4}·\sqrt{3}\) Simplificar. \(2\sqrt{3}\) 2. \((4\sqrt{3})(2\sqrt{12})\) Multiplicar usando la Propiedad del Producto. \(8\sqrt{36}\) Simplifica lo radical. \(8·6\) Simplificar. \(48\)
Simplificar:
- \(\sqrt{3}·\sqrt{6}\)
- \((2\sqrt{6})(3\sqrt{12})\).
- Contestar
-
- \(3\sqrt{2}\)
- \(36\sqrt{2}\)
Simplificar:
- \(\sqrt{5}·\sqrt{10}\)
- \((6\sqrt{3})(5\sqrt{6})\)
- Contestar
-
- \(5\sqrt{2}\)
- \(90\sqrt{2}\)
Simplificar:\((6\sqrt{2})(3\sqrt{10})\)
- Contestar
-
\((6\sqrt{2})(3\sqrt{10})\) Multiplicar usando la Propiedad del Producto. \(18\sqrt{20}\) Simplifica lo radical. \(18\sqrt{4}·\sqrt{5}\) Simplificar. \(18·2·\sqrt{5}\) \(36\sqrt{5}\)
Simplificar:\((3\sqrt{2})(2\sqrt{30})\)
- Contestar
-
\(12\sqrt{15}\)
Simplificar:\((3\sqrt{3})(3\sqrt{6})\).
- Contestar
-
\(27\sqrt{2}\)
Cuando tenemos que multiplicar raíces cuadradas, primero encontramos el producto y luego eliminamos cualquier factor cuadrado perfecto.
Simplificar:
- \((\sqrt{8x^3})(\sqrt{3x})\)
- \((\sqrt{20y^2})(\sqrt{5y^3})\)
- Contestar
-
1. \((\sqrt{8x^3})(\sqrt{3x})\) Multiplicar usando la Propiedad del Producto. \(\sqrt{24x^4}\) Simplifica lo radical. \(\sqrt{4x^4}·\sqrt{6}\) Simplificar. \(2x^2\sqrt{6}\) 2. \((\sqrt{20y^2})(\sqrt{5y^3})\) Multiplicar usando la Propiedad del Producto. \(\sqrt{100y^5}\) Simplifica lo radical. \(10y^2\sqrt{y}\)
Simplificar:
- \((\sqrt{6x^3})(\sqrt{3x})\)
- \((\sqrt{2y^3})(\sqrt{50y^2})\).
- Contestar
-
- \(3x^2\sqrt{2}\)
- \(10y^2\sqrt{y}\)
Simplificar:
- \((\sqrt{6x^5})(\sqrt{2x})\)
- \((\sqrt{12y^2})(\sqrt{3y^5})\)
- Contestar
-
- \(2x^3\sqrt{3}\)
- \(6y^2\sqrt{y}\)
Simplificar:\((10\sqrt{6p^3})(3\sqrt{18p})\)
- Contestar
-
\((10\sqrt{6p^3})(3\sqrt{18p})\) Multiplicar. \(30\sqrt{108p^4}\) Simplifica lo radical. \(30\sqrt{36p^4}·\sqrt{3}\) \(30·6p^2·\sqrt{3}\) \(180p^2\sqrt{3}\)
Simplificar:\((\sqrt{62x^2})(8\sqrt{45x^4})\)
- Contestar
-
\(144x^3\sqrt{10}\)
Simplificar:\((2\sqrt{6y^4})(12\sqrt{30y})\).
- Contestar
-
\(144y^2\sqrt{5y}\)
Simplificar:
- \((\sqrt{2})^2\)
- \((−\sqrt{11})^2\).
- Contestar
-
1. \((\sqrt{2})^2\) Reescribir como producto. \((\sqrt{2})(\sqrt{2})\) Multiplicar. \(\sqrt{4}\) Simplificar. 2 2. \((−\sqrt{11})^2\) Reescribir como producto. \((−\sqrt{11})(−\sqrt{11})\) Multiplicar. \(\sqrt{121}\) Simplificar. 11
Simplificar:
- \((\sqrt{12})^2\)
- \((−\sqrt{15})^2\).
- Contestar
-
- 12
- 15
Simplificar:
- \((\sqrt{16})^2\)
- \((−\sqrt{20})^2\).
- Contestar
-
- 16
- 20
Los resultados del ejemplo anterior nos llevan a esta propiedad.
Si a es un número real no negativo, entonces
\((\sqrt{a})^2=a\)
Al darnos cuenta de que cuadrar y tomar una raíz cuadrada son operaciones 'opuestas', podemos simplificar\((\sqrt{2})^2\) y obtener 2 de inmediato. Cuando multiplicamos las dos como raíces cuadradas en la parte (a) del siguiente ejemplo, es lo mismo que cuadrar.
Simplificar:
- \((2\sqrt{3})(8\sqrt{3})\)
- \((3\sqrt{6})^2\).
- Contestar
-
1. \((2\sqrt{3})(8\sqrt{3})\) Multiplicar. Recuerda,\((\sqrt{3}^2)\) 16·3 Simplificar. 48 2. \((3\sqrt{6})^2\) Multiplicar. 9·6 Simplificar. 54
Simplificar:
- \((6\sqrt{11})(5\sqrt{11})\)
- \((5\sqrt{8})^2\).
- Contestar
-
- 330
- 200
Simplificar:
- \((3\sqrt{7})(10\sqrt{7})\)
- \((−4\sqrt{6})^2\).
- Contestar
-
- 210
- 96
Usa Multiplicación Polinomial para Multiplicar Raíces Cuadradas
En los siguientes ejemplos, usaremos la Propiedad Distributiva para multiplicar expresiones con raíces cuadradas.
Primero distribuiremos y luego simplificaremos las raíces cuadradas cuando sea posible.
Simplificar:
- \(3(5−\sqrt{2})\)
- \(\sqrt{2}(4−\sqrt{10})\).
- Contestar
-
1. \(3(5−\sqrt{2})\) Distribuir. \(15−3\sqrt{2})\) 2. \(\sqrt{2}(4−\sqrt{10})\) Distribuir. \(4\sqrt{2}−\sqrt{20}\) Simplificar. \(4\sqrt{2}−2\sqrt{5}\)
Simplificar:
- \(2(3−\sqrt{5})\)
- \(\sqrt{3}(2−\sqrt{18})\).
- Contestar
-
- \(6−2\sqrt{5}\)
- \(2\sqrt{3}−3\sqrt{6}\)
Simplificar:
- \(6(2+\sqrt{6})\)
- \(\sqrt{7}(1+\sqrt{14})\).
- Contestar
-
- \(12+\sqrt{6}\)
- \(\sqrt{7}+7\sqrt{2}\)
Simplificar:
- \(\sqrt{5}(7+2\sqrt{5})\)
- \(\sqrt{6}(\sqrt{2}+\sqrt{18})\).
- Contestar
-
1. \(\sqrt{5}(7+2\sqrt{5})\) Distribuir. \(7\sqrt{5}+2·5\) Simplificar. \(7\sqrt{5}+10\) \(10+7\sqrt{5}\) 2. \(\sqrt{6}(\sqrt{2}+\sqrt{18})\) Multiplicar. \(\sqrt{12}+\sqrt{108}\) Simplificar. \((\sqrt{4}·\sqrt{3}+\sqrt{36}·\sqrt{3})\) \(2\sqrt{3}+6\sqrt{3}\) Combina como radicales. \(8\sqrt{3}\)
Simplificar:
- \(\sqrt{6}(1+3\sqrt{6})\)
- \(\sqrt{12}(\sqrt{3}+\sqrt{24})\)
- Contestar
-
- \(18+\sqrt{6}\)
- \(6+12\sqrt{2}\)
Simplificar:
- \(\sqrt{8}(2−5\sqrt{8})\)
- \(\sqrt{14}(\sqrt{2}+\sqrt{42})\)
- Contestar
-
- \(−40+4\sqrt{2}\)
- \(2\sqrt{7}+14\sqrt{3}\)
Cuando trabajamos con polinomios, multiplicamos binomios por binomios. Recuerda, esto nos dio cuatro productos antes de combinar cualquier término similar. Para asegurarnos de obtener los cuatro productos, organizamos nuestro trabajo, generalmente por el método FOIL.
Simplificar:\((2+\sqrt{3})(4−\sqrt{3})\)
- Contestar
-
\((2+\sqrt{3})(4−\sqrt{3})\) Multiplicar. \(8−2\sqrt{3}+4\sqrt{3}−3\) Combina términos similares. \(5+2\sqrt{3}\)
Simplificar:\((1+\sqrt{6})(3−\sqrt{6})\).
- Contestar
-
\(−3+2\sqrt{6}\)
Simplificar:\((4−\sqrt{10})(2+\sqrt{10})\).
- Contestar
-
\(−2+2\sqrt{10}\)
Simplificar:\((3−2\sqrt{7})(4−2\sqrt{7})\).
- Contestar
-
\((3−2\sqrt{7})(4−2\sqrt{7})\) Multiplicar. \(12−6\sqrt{7}−8\sqrt{7}+4·7\) Simplificar. \(12−6\sqrt{7}−8\sqrt{7}+28\) Combina términos similares. \(40−14\sqrt{7}\)
Simplificar:\((6−3\sqrt{7})(3+4\sqrt{7})\).
- Contestar
-
\(−66+15\sqrt{7}\)
Simplificar:\((2−3\sqrt{11})(4−\sqrt{11})\)
- Contestar
-
\(41+14\sqrt{11}\)
Simplificar:\((3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})\).
- Contestar
-
\(3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})\) Multiplicar. \(3·2+12\sqrt{10}−\sqrt{10}−4·5\) Simplificar. \(6+12\sqrt{10}−\sqrt{10}−20\) Combina términos similares. \(−14+11\sqrt{10}\)
Simplificar:\((5\sqrt{3}−\sqrt{7})(\sqrt{3}+2\sqrt{7})\)
- Contestar
-
\(1+9\sqrt{21}\)
Simplificar:\((\sqrt{6}−3\sqrt{8})(2\sqrt{6}+\sqrt{8})\)
- Contestar
-
\(−12−20\sqrt{3}\)
Simplificar:\((4−2\sqrt{x})(1+3\sqrt{x})\).
- Contestar
-
\((4−2\sqrt{x})(1+3\sqrt{x})\). Multiplicar. \(4+12\sqrt{x}−2\sqrt{x}−6x\) Combina términos similares. \(4+10\sqrt{x}−6x\)
Simplificar:\((6−5\sqrt{m})(2+3\sqrt{m})\).
- Contestar
-
\(12+8\sqrt{m}−15m\)
Simplificar:\((10+3\sqrt{n})(1−5\sqrt{n})\)
- Contestar
-
\(10−47\sqrt{n}−15n\)
Tenga en cuenta que algunos productos especiales facilitaron nuestro trabajo cuando multiplicamos binomios antes. Esto es cierto cuando multiplicamos las raíces cuadradas, también. A continuación se muestran las fórmulas especiales de productos que utilizamos.
\[\begin{array}{ll} {\textbf{Binomial Squares}}&{\textbf{Product of Conjugates}}\\ {(a+b)^2=a^2+2ab+b^2}&{(a−b)(a+b)=a^2−b^2}\\ {(a−b)^2=a^2−2ab+b^2}&{}\\ \nonumber \end{array}\]
Usaremos las fórmulas especiales de productos en los siguientes ejemplos. Comenzaremos con la fórmula Cuadrados Binomiales.
Simplificar:
- \((2+\sqrt{3})^2\)
- \((4−2\sqrt{5})^2\).
- Contestar
-
Asegúrese de incluir el término 2ab al cuadrar un binomio.
1.
2.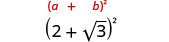
Multiplicar usando el patrón cuadrado binomial. 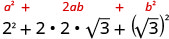
Simplificar. 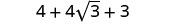
Combina términos similares. 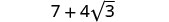
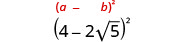
Multiplicar usando el patrón cuadrado binomial. 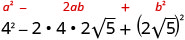
Simplificar. 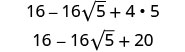
Combina términos similares. 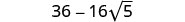
Simplificar:
- \((10+\sqrt{2})^2\)
- \((1+3\sqrt{6})^2\).
- Contestar
-
- \(102+20\sqrt{2}\)
- \(55+6\sqrt{6}\)
Simplificar:
- \((6-\sqrt{5})^2\)
- \((9-2\sqrt{10})^2\).
- Contestar
-
- \(41-12\sqrt{5}\)
- \(121-36\sqrt{10}\)
Simplificar:\((1+3\sqrt{x})^2\).
- Contestar
-
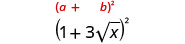
Multiplicar usando el patrón cuadrado binomial. 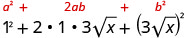
Simplificar. 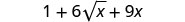
Simplificar:\((2+5\sqrt{m})^2\).
- Contestar
-
\(4+20\sqrt{m}+25m\)
Simplificar:\((3−4\sqrt{n})^2\).
- Contestar
-
\(9−24\sqrt{n}+16n\)
En los dos siguientes ejemplos, encontraremos el producto de los conjugados.
Simplificar:\((4−\sqrt{2})(4+\sqrt{2})\).
- Contestar
-
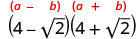
Multiplicar usando el patrón cuadrado binomial. 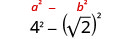
Simplificar. 
Simplificar:\((2−\sqrt{3})(2+\sqrt{3})\)
- Contestar
-
1
Simplificar:\((1+\sqrt{5})(1−\sqrt{5})\)
- Contestar
-
−4
Simplificar:\((5−2\sqrt{3})(5+2\sqrt{3})\)
- Contestar
-
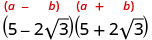
Multiplicar usando el patrón cuadrado binomial. 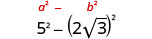
Simplificar. 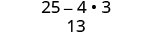
Simplificar:\((3−2\sqrt{5})(3+2\sqrt{5})\).
- Contestar
-
−11
Simplificar:\((4+5\sqrt{7})(4−5\sqrt{7})\).
- Contestar
-
−159
Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con multiplicar raíces cuadradas.
- Propiedad del producto
- Multiplicar binomios con raíces cuadradas
Conceptos clave
- Propiedad del producto de las raíces cuadradas Si a, b son números reales no negativos, entonces
\(\sqrt{ab}=\sqrt{a·b}\)y\(\sqrt{a}·\sqrt{b}=\sqrt{ab}\)
- Fórmulas especiales para multiplicar binomios y conjugados:
\[\begin{array}{ll} {(a+b)^2=a^2+2ab+b^2}&{(a−b)(a+b)=a^2−b^2}\\ {(a−b)^2=a^2−2ab+b^2 }&{}\\ \nonumber \end{array}\]
- El método FOIL se puede utilizar para multiplicar binomios que contienen radicales.


