Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

9.7: Raíces superiores

Última actualización

30 oct 2022
Guardar como PDF
- 9.6E: Ejercicios
- 9.7E: Ejercicios

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Al final de esta sección, podrás:

Simplifica expresiones con raíces superiores
Utilice la propiedad Product para simplificar expresiones con raíces más altas
Utilice la propiedad Cocient para simplificar expresiones con raíces más altas
Sumar y restar raíces superiores

Nota

Simplificar: $y^{5}y^{4}$ .
Si te perdiste este problema, revisa el Ejemplo 6.2.7.
Simplificar: $(n^2)^6$ .
Si te perdiste este problema, revisa el Ejemplo 6.2.19.
Simplificar: $\frac{x^8}{x^3}$ .
Si te perdiste este problema, revisa el Ejemplo 6.5.1.

Simplifique las expresiones con raíces superiores

Hasta ahora, en este capítulo hemos trabajado con cuadrados y raíces cuadradas. Ahora ampliaremos nuestro trabajo para incluir poderes superiores y raíces superiores.

Revisemos un poco de vocabulario primero.

$\begin{array}{cc} {}&{}\\ {\textbf{We write:}}&{\textbf{We say:}}\\ {n^2}&{\text{n squared}}\\ {n^3}&{\text{n cubed}}\\ {n^4}&{\text{n to the fourth}}\\ {n^5}&{\text{n to the fifth}}\\ \nonumber \end{array}$

Los términos 'cuadrado' y 'cubo' provienen de las fórmulas para área de un cuadrado y volumen de un cubo.

Será útil tener una tabla de las potencias de los enteros de −5to5. Ver Figura $\PageIdnex{1}$ .

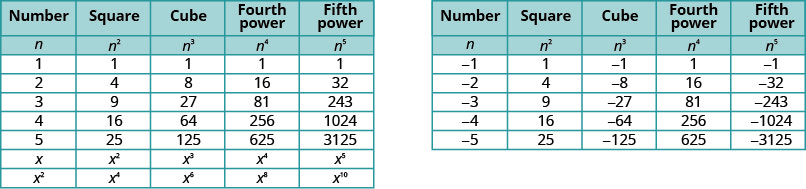
Esta cifra consta de dos tablas. En la primera tabla se muestran los resultados de elevar los números 1, 2, 3, 4, 5, x y x al cuadrado a la segunda, tercera, cuarta y quinta potencias. En la segunda tabla se muestran los resultados de elevar los números negativos uno a cinco negativos a la segunda, tercera, cuarta y quinta potencias. La tabla primero tiene cinco columnas y nueve filas. El segundo tiene cinco columnas y siete filas. Las columnas en ambas tablas están etiquetadas como “Número”, “Cuadrado”, “Cubo”, “Cuarto poder”, “Quinto poder”, nada, “Número”, “Cuadrado”, “Cubo”, “Cuarto poder” y “Quinto poder”. En ambas tablas, la siguiente fila dice: n, n al cuadrado, n al cubo, n al cuarto poder, n al quinto poder, nada, n, n al cuadrado, n al cubo, n al cuarto poder, y n al quinto poder. En la primera tabla, 1 al cuadrado, 1 al cubo, 1 a la cuarta potencia y 1 a la quinta potencia se muestran todos como 1. En la siguiente fila, 2 al cuadrado es 4, 2 cubos es 8, 2 a la cuarta potencia es 16, y 2 a la quinta potencia es 32. En la siguiente fila, 3 al cuadrado es 9, 3 cubos es 27, 3 a la cuarta potencia es 81, y 3 a la quinta potencia es 243. En la siguiente fila, 4 al cuadrado es 16, 4 cubos es 64, 4 a la cuarta potencia es 246, y 4 a la quinta potencia es 1024. En la siguiente fila, 5 al cuadrado es 25, 5 cubos es 125, 5 a la cuarta potencia es 625, y 5 a la quinta potencia es 3125. En la siguiente fila se listan x al cuadrado, x en cubos, x a la cuarta potencia y x a la quinta potencia. En la siguiente fila, x cuadrado es x a la cuarta potencia, x cubicado al cuadrado es x a la quinta potencia, x cuadrado a la cuarta potencia es x a la octava potencia, y x cuadrado a la quinta potencia es x a la décima potencia. En la segunda tabla, negativo 1 cuadrado es 1, negativo 1 cubo es negativo 1, negativo 1 a la cuarta potencia es 1, y negativo 1 a la quinta potencia es negativo 1. En la siguiente fila, negativo 2 al cuadrado es 4, negativo 2 al cubo es negativo 8, negativo 2 a la cuarta potencia es 16, y negativo 2 a la quinta potencia es negativo 32. En la siguiente fila, negativo 4 al cuadrado es 16, negativo 4 al cubo es negativo 64, negativo 4 a la cuarta potencia es 256, y negativo 4 a la quinta potencia es negativo 1024. En la siguiente fila, negativo 5 cuadrado es 25, negativo 5 cubos es negativo 125, negativo 5 a la cuarta potencia es 625, y negativo 5 a la quinta potencia es negativo 3125. — Figura $\PageIndex{1}$ : Poderes primero a quinto de enteros de −5 a 5.

Observe los signos en la Figura $\PageIndex{1}$ . Todos los poderes de los números positivos son positivos, claro. Pero cuando tenemos un número negativo, los poderes pares son positivos y los impares son negativos. Copiaremos la fila con los poderes de −2 a continuación para ayudarte a ver esto.

$Esta cifra tiene cinco columnas y dos filas. La primera fila etiqueta cada columna: n, n al cuadrado, n en cubos, n a la cuarta potencia y n a la quinta potencia. La segunda fila dice: negativo 2, 4, negativo 8, 16 y negativo 32.$

Anteriormente en este capítulo definimos la raíz cuadrada de un número.

Si $n^2=m$ , entonces n es una raíz cuadrada de m.

Y hemos utilizado la notación $\sqrt{m}$ para denotar la raíz cuadrada principal. Así que $\sqrt{m} \ge 0$ siempre.

Ahora extenderemos la definición a raíces superiores.

Definición: N TH RAÍZ DE UN NÚMERO

Si $b^n=a$ , entonces b es una raíz n ésima de un número a.

La raíz principal n th de a está escrita $\sqrt[n]{a}=b$

n se llama el índice del radical.

No escribimos el índice para una raíz cuadrada. Al igual que usamos la palabra 'cubos' para $b^3$ , usamos el término 'raíz cúbica' para $\sqrt[3]{a}$ .

Nos referimos $\PageIndex{1}$ a Figura para ayudarnos a encontrar raíces superiores.

$\begin{array}{cc} {4^3=64}&{\sqrt[3]{64}=4}\\ {3^4=81}&{\sqrt[4]{81}=3}\\ {(−2)^5=−32}&{\sqrt[5]{−32}=−2}\\ \nonumber \end{array}$

¿Podríamos tener una raíz par de un número negativo? No. Sabemos que la raíz cuadrada de un número negativo no es un número real. Lo mismo es cierto para cualquier raíz par. Incluso las raíces de los números negativos no son números reales. Las raíces impares de números negativos son números reales.

Definición: PROPIEDADES DE $\sqrt[n]{a}$

Cuando n es un número par y

$a\ge 0$ , entonces $\sqrt[n]{a}$ es un número real
$a < 0$ , entonces no $\sqrt[n]{a}$ es un número real

Cuando n es un número impar, $\sqrt[n]{a}$ es un número real para todos los valores de a.

Ejemplo $\PageIndex{1}$

Simplificar:

$\sqrt[3]{8}$
$\sqrt[4]{81}$
$\sqrt[5]{32}$ .

Responder

1.	$\sqrt[3]{8}$
Ya que $(2)^3=8$ .	2
2.	$\sqrt[4]{81}$
Ya que $(3)^4=81$ .	3
3.	$\sqrt[5]{32}$
Ya que $(2)^5=32$ .	2

Ejemplo $\PageIndex{2}$

Simplificar:

$\sqrt[3]{27}$
$\sqrt[4]{256}$
$\sqrt[5]{243}$ .

Responder

Ejemplo $\PageIndex{3}$

Simplificar:

$\sqrt[3]{1000}$
$\sqrt[4]{16}$
$\sqrt[5]{32}$ .

Responder

Ejemplo $\PageIndex{4}$

Simplificar:

$\sqrt[3]{−64}$
$\sqrt[4]{−16}$
$\sqrt[5]{−243}$ .

Responder

1.	$\sqrt[3]{−64}$
Ya que $(−4)^3=−64$ .	−4
2.	$\sqrt[4]{−16}$
Piensa, $(?)^4=−16$ .Ningún número real elevado a la cuarta potencia es positivo.	No es un número real.
3.	$\sqrt[5]{−243}$
Ya que $(−3)^5=−243$ .	−3

Ejemplo $\PageIndex{5}$

Simplificar:

$\sqrt[3]{−125}$
$\sqrt[4]{−16}$
$\sqrt[5]{−32}$ .

Responder

−5
no real
−2

Ejemplo $\PageIndex{6}$

Simplificar:

$\sqrt[3]{−216}$
$\sqrt[4]{−81}$
$\sqrt[5]{−1024}$ .

Responder

−6
no real
−4

Cuando trabajamos con raíces cuadradas que tenían variables en el radicando, restringimos las variables a valores no negativos. Ahora vamos a eliminar esta restricción.

La raíz impar de un número puede ser positiva o negativa. Eso lo hemos visto $\sqrt[3]{−64}=−4$ .

Pero la raíz par de un número no negativo siempre es no negativa, porque tomamos la raíz n th principal.

Supongamos que empezamos con a=−5.

$\begin{array}{cc} {(−5)^4=625}&{\sqrt[4]{625}=5}\\ \nonumber \end{array}$

¿Cómo podemos asegurarnos de que la cuarta raíz de −5 elevada a la cuarta potencia, $(−5)^4$ sea 5? Veremos en la siguiente propiedad.

Definición: SIMPLIFICACIÓN DE RAÍCES PARES Y

Para cualquier entero $n \ge 2$ ,

$\begin{array}{cc} {\text{when n is odd}}&{\sqrt[n]{a^n}=a}\\ {\text{when n is even}}&{\sqrt[n]{a^n}=|a|}\\ \nonumber \end{array}$

Debemos usar los signos de valor absoluto cuando tomamos una raíz par de una expresión con una variable en el radical.

Ejemplo $\PageIndex{7}$

Simplificar:

$\sqrt{x^2}$
$\sqrt[3]{n^3}$
$\sqrt[4]{p^4}$
$\sqrt[5]{y^5}$ .

Responder

Usamos el valor absoluto para asegurarnos de obtener la raíz positiva.

1.	$\sqrt{x^2}$
Desde $(x)^2=x^2$ y queremos la raíz positiva.	\|x\|
2.	$\sqrt[3]{n^3}$
Ya que $(n)^3=n^3$ . Es una raíz impar por lo que no hay necesidad de un signo de valor absoluto.	n
3.	$\sqrt[4]{p^4}$
Desde $(p)^4=p^4$ y queremos la raíz positiva.	\|p\|
4.	$\sqrt[5]{y^5}$
Ya que $(y)^5=y^5$ . Es una raíz impar por lo que no hay necesidad de un signo de valor absoluto.	y

Ejemplo $\PageIndex{8}$

Simplificar:

$\sqrt{b^2}$
$\sqrt[3]{w^3}$
$\sqrt[4]{m^4}$
$\sqrt[5]{q^5}$ .

Responder

Ejemplo $\PageIndex{9}$

Simplificar:

$\sqrt{y^2}$
$\sqrt[3]{p^3}$
$\sqrt[4]{z^4}$
$\sqrt[5]{q^5}$

Responder

Ejemplo $\PageIndex{10}$

Simplificar:

$\sqrt[3]{y^{18}}$
$\sqrt[4]{z^8}$ .

Responder

1.	$\sqrt[3]{y^{18}}$
Ya que $(y^6)^3=y^18$ .	$\sqrt[3]{(y^6)^3}$
	$y^6$
2.	$\sqrt[4]{z^8}$
Ya que $(z^2)^4=z^8$ .	$\sqrt[4]{(z^2)^4}$
Ya que $z^2$ es positivo, no necesitamos un signo de valor absoluto.	$z^2$

Ejemplo $\PageIndex{11}$

Simplificar:

$\sqrt[4]{u^{12}}$
$\sqrt[3]{v^{15}}$ .

Responder

$u^3$
$v^5$

Ejemplo $\PageIndex{12}$

Simplificar:

$\sqrt[5]{c^{20}}$
$\sqrt[6]{d^{24}}$ .

Responder

$c^4$
$d^4$

Ejemplo $\PageIndex{13}$

Simplificar:

$\sqrt[3]{64p^6}$
$\sqrt[4]{16q^{12}}$ .

Responder

1.	$\sqrt[3]{64p^6}$
Reescribir $64p^6$ como $(4p^2)^3$ .	$\sqrt[3]{(4p^2)^3}$
Toma la raíz cubicada.	$4p^2$
2.	$\sqrt[4]{16q^{12}}$
Reescribir el radicando como un cuarto poder.	$\sqrt[4]{(2q^3)^4}$
Toma la cuarta raíz.	$2\|q^3\|$

Ejemplo $\PageIndex{14}$

Simplificar:

$\sqrt[3]{27x^{27}}$
$\sqrt[4]{81q^{28}}$ .

Responder

$3x^9$
$3∣q^7∣$

Ejemplo $\PageIndex{15}$

Simplificar:

$\sqrt[3]{125p^9}$
$\sqrt[5]{243q^{25}}$

Responder

$5p^3$
$3q^5$

Utilice la propiedad Product para simplificar expresiones con raíces más altas

Simplificaremos las expresiones con raíces superiores de la misma manera que simplificamos las expresiones con raíces cuadradas. Una raíz n th se considera simplificada si no tiene factores de $m^n$ .

Definición: RAÍZ SIMPLIFICADA

$\sqrt[n]{a}$ se considera simplificado si a no tiene factores de $m^n$ .

Generalizaremos la Propiedad del Producto de Raíces Cuadradas para incluir cualquier raíz entera $n \ge 2$ .

Definición: PROPIEDAD DE PRODUCTO DE N TH ROOTS

$\sqrt[n]{ab}=\sqrt[n]{a}·\sqrt[n]{b}$ y $\sqrt[n]{a}·\sqrt[n]{b}=\sqrt[n]{ab}$

cuando $\sqrt[n]{a}$ y $\sqrt[n]{b}$ son números reales y para cualquier entero $n \ge 2$

Ejemplo $\PageIndex{16}$

Simplificar:

$\sqrt[3]{x^4}$
$\sqrt[4]{x^7}$ .

Responder

1.	$\sqrt[3]{x^4}$
Reescribe el radicand como un producto usando el factor cubo perfecto más grande.	$\sqrt[3]{x^3·x}$
Reescribir el radical como producto de dos radicales.	$\sqrt[3]{x^3}·\sqrt[3]{x}$
Simplificar.	$x\sqrt[3]{x}$
2.	$\sqrt[4]{x^7}$
Reescribe el radicando como producto usando el cuarto factor de potencia perfecto más grande.	$\sqrt[4]{x^4·x^3}$
Reescribir el radical como producto de dos radicales.	$\sqrt[4]{x^4}·\sqrt[4]{x^3}$
Simplificar.	$\|x\|\sqrt[4]{x^3}$

Ejemplo $\PageIndex{17}$

Simplificar:

$\sqrt[4]{y^6}$
$\sqrt[3]{z^5}$ .

Responder

$|y∣\sqrt[4]{y^2}$
$z\sqrt[3]{z^2}$

Ejemplo $\PageIndex{18}$

Simplificar:

$\sqrt[5]{p^8}$
$\sqrt[6]{q^{13}}$ .

Responder

$p\sqrt[5]{p^3}$
$q^2\sqrt[6]{q}$

Ejemplo $\PageIndex{19}$

Simplificar:

$\sqrt[3]{16}$
$\sqrt[4]{243}$ .

Responder

1.	$\sqrt[3]{16}$
	$\sqrt[3]{2^4}$
Reescribe el radicand como un producto usando el factor cubo perfecto más grande.	$\sqrt[3]{2^3·2}$
Reescribir el radical como producto de dos radicales.	$\sqrt[3]{2^3}·\sqrt[3]{2}$
Simplificar.	$2\sqrt[3]{2}$
2.	$\sqrt[4]{243}$
	$\sqrt[4]{3^5}$
Reescribe el radicando como producto usando el cuarto factor de potencia perfecto más grande.	$\sqrt[4]{3^4·3}$
Reescribir el radical como producto de dos radicales.	$\sqrt[4]{3^4}·\sqrt[4]{3}$
Simplificar.	$3\sqrt[4]{3}$

Ejemplo $\PageIndex{20}$

Simplificar:

$\sqrt[3]{81}$
$\sqrt[4]{64}$ .

Responder

$3\sqrt[3]{3}$
$2\sqrt[4]{4}$

Ejemplo $\PageIndex{21}$

Simplificar:

$\sqrt[3]{625}$
$\sqrt[4]{729}$ .

Responder

$5\sqrt[3]{5}$
$3\sqrt[4]{9}$

No olvides usar los signos de valor absoluto al tomar una raíz par de una expresión con una variable en el radical.

Ejemplo $\PageIndex{22}$

Simplificar:

$\sqrt[3]{24x^7}$
$\sqrt[4]{80y^{14}}$ .

Responder

1.	$\sqrt[3]{24x^7}$
Reescribe el radicando como un producto usando factores de cubo perfectos.	$\sqrt[3]{2^{3}x^{6}·3x}$
Reescribir el radical como producto de dos radicales.	$\sqrt[3]{2^{3}x^{6}}·\sqrt[3]{3x}$
Reescribe el primer radicando como $(2x^2)^3$	$\sqrt[3]{(2x^{2})^3}·\sqrt[3]{3x}$
Simplificar.	$2x^2\sqrt[3]{3x}$
2.	$\sqrt[4]{80y^{14}}$
Reescribe el radicando como producto usando cuatro factores de potencia perfectos.	$\sqrt[4]{2^{4}y^{12}·5y^2}$
Reescribir el radical como producto de dos radicales.	$\sqrt[4]{2^{4}y^{12}}·\sqrt[4]{5y^2}$
Reescribe el primer radicando como $(2y^3)^4$	$\sqrt[4]{(2y^3)^4}·\sqrt[4]{5y^2}$
Simplificar.	$2\|y^3\|\sqrt[4]{5y^2}$

Ejemplo $\PageIndex{23}$

Simplificar:

$\sqrt[3]{54p^[10}]$
$\sqrt[4]{64q^{10}}$ .

Responder

$3p^3\sqrt[3]{2p}$
$2q^2\sqrt[4]{4q^2}$

Ejemplo $\PageIndex{24}$

Simplificar:

$\sqrt[3]{128m^{11}}$
$\sqrt[4]{162n^7}$ .

Responder

$4m^3\sqrt[3]{2m^2}$
$3|n|\sqrt[4]{2n^3}$

Ejemplo $\PageIndex{25}$

Simplificar:

$\sqrt[3]{−27}$
$\sqrt[4]{−16}$ .

Responder

1.	$\sqrt[3]{−27}$
Reescribe el radicando como un producto usando factores de cubo perfectos.	$\sqrt[3]{(−3)^3}$
Toma la raíz cubicada.	−3
2.	$\sqrt[4]{−16}$
No hay número real n donde $n^4=−16$ .	No es un número real.

Ejemplo $\PageIndex{26}$

Simplificar:

$\sqrt[3]{−108}$
$\sqrt[4]{−48}$ .

Responder

$−3\sqrt[3]{4}$
no real

Ejemplo $\PageIndex{27}$

Simplificar:

$\sqrt[3]{−625}$
$\sqrt[4]{−324}$ .

Responder

$−5\sqrt[3]{5}$
no real

Utilice la propiedad Cocient para simplificar expresiones con raíces más altas

Podemos simplificar las raíces más altas con cocientes de la misma manera que simplificamos las raíces cuadradas. Primero simplificamos cualquier fracción dentro del radical.

Ejemplo $\PageIndex{28}$

Simplificar:

$\sqrt[3]{\frac{a^8}{a^5}}$
$\sqrt[4]{\frac{a^{10}}{a^2}}$ .

Responder

1.	$\sqrt[3]{\frac{a^8}{a^5}}$
Simplifique primero la fracción bajo el radical.	$\sqrt[3]{a^3}$
Simplificar.	a
2.	$\sqrt[4]{\frac{a^{10}}{a^2}}$
Simplifique primero la fracción bajo el radical.	$\sqrt[4]{a^8}$
Reescribe el radicando usando cuatro factores de potencia perfectos.	$\sqrt[4]{(a^2)^4}$
Simplificar.	$a^2$

Ejemplo $\PageIndex{29}$

Simplificar:

$\sqrt[4]{\frac{x^7}{x^3}}$
$\sqrt[4]{\frac{y^{17}}{y^5}}$ .

Responder

|x|
$y^3$

Ejemplo $\PageIndex{30}$

Simplificar:

$\sqrt[3]{\frac{m^{13}}{m^7}}$
$\sqrt[5]{\frac{n^{12}}{n^2}}$ .

Responder

$m^2$
$n^2$

Anteriormente, se utilizó la Propiedad Cociente 'a la reversa' para simplificar las raíces cuadradas. Ahora generalizaremos la fórmula para incluir raíces superiores.

Definición: PROPIEDAD COCIENTE DE LAS RAÍCES N TH

$\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$ y $\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}$

cuando $\sqrt[n]{a}$ and $\sqrt[n]{b}$ are real numbers, $b \ne 0$ , and for any integer $n \ge 2$

Ejercicio $\PageIndex{31}$

Simplificar:

$\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}$
$\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}$

Responder

1.	$\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}$
Ni radicand es un cubo perfecto, así que usa la Propiedad Cociente para escribir como un radical.	$\sqrt[3]{\frac{−108}{2}}$
Simplifica la fracción bajo el radical.	$\sqrt[3]{−54}$
Reescribe el radicando como un producto usando factores de cubo perfectos.	$\sqrt[3]{(−3)^3·2}$
Reescribir el radical como producto de dos radicales.	$\sqrt[3]{(−3)^3}·\sqrt[3]{2}$
Simplificar.	$−3\sqrt[3]{2}$
2.	$\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}$
Ni radicando es un cuarto poder perfecto, así que usa la Propiedad Cociente para escribir como un solo radical	$\sqrt[4]{\frac{96x^7}{3x^2}}$
Simplifica la fracción bajo el radical.	$\sqrt[4]{32x^5}$
Reescribe el radicando como producto usando cuatro factores de potencia perfectos.	$\sqrt[4]{2^{4}x^4·2x}$
Reescribir el radical como producto de dos radicales.	$\sqrt[4]{(2x)^4}·\sqrt[4]{2x}$
Simplificar.	$2\|x\|\sqrt[4]{2x}$

Ejemplo $\PageIndex{32}$

Simplificar:

$\frac{\sqrt[3]{−532}}{\sqrt[3]{2}}$
$\frac{\sqrt[4]{486m^{11}}}{\sqrt[4]{3m^5}}$

Responder

no real
$3|m|\sqrt[4]{2m^2}$

Ejemplo $\PageIndex{33}$

Simplificar:

$\frac{\sqrt[3]{−192}}{\sqrt[3]{3}}$
$\frac{\sqrt[4]{324n^7}}{\sqrt[4]{2n^3}}$ .

Responder

−4
$3|n|\sqrt[4]{2}$

Si la fracción dentro del radical no puede simplificarse, utilizamos la primera forma de la Propiedad Cociente para reescribir la expresión como el cociente de dos radicales.

Ejemplo $\PageIndex{34}$

Simplificar:

$\sqrt[3]{\frac{24x^7}{y^3}}$
$\sqrt[4]{\frac{48x^{10}}{y^8}}$ .

Responder

1.	$\sqrt[3]{\frac{24x^7}{y^3}}$
La fracción en el radicando no puede simplificarse. Utilice la Propiedad Cociente para escribir como dos radicales.	$\frac{\sqrt[3]{24x^7}}{\sqrt[3]{y^3}}$
Reescribe cada radicando como un producto usando factores de cubo perfectos.	$\frac{\sqrt[3]{8x^6·3x}}{\sqrt[3]{y^3}}$
Reescribe el numerador como producto de dos radicales.	$\frac{\sqrt[3]{(2x^2)^3}·\sqrt[3]{3x}}{\sqrt[3]{y^3}}$
Simplificar.	$\frac{2x^2\sqrt[3]{3x}}{y}$
2.	$\sqrt[4]{\frac{48x^{10}}{y^8}}$
La fracción en el radicando no puede simplificarse. Utilice la Propiedad Cociente para escribir como dos radicales.	$\frac{\sqrt[4]{48x^{10}}}{\sqrt[4]{y^8}}$
Reescribe cada radicando como un producto usando factores de cubo perfectos.	$\frac{\sqrt[4]{16x^8·3x^2}}{\sqrt[4]{y^8}}$
Reescribe el numerador como producto de dos radicales.	$\frac{\sqrt[4]{(2x^2)^4}·\sqrt[4]{3x^2}}{\sqrt[4]{(y^2)^4}}$
Simplificar.	$\frac{2x^2\sqrt[4]{3x^2}}{y^2}$

Ejemplo $\PageIndex{35}$

Simplificar:

$\sqrt[3]{\frac{108c^{10}}{d^6}}$
$\sqrt[4]{\frac{80x^{10}}{y^5}}$ .

Responder

$\frac{3c^3\sqrt[3]{4c}}{d^2}$
$\frac{x^2}{∣y∣}\sqrt[4]{\frac{80x^2}{y}}$

Ejemplo $\PageIndex{36}$

Simplificar:

$\sqrt[3]{\frac{40r^3}{s}}$
$\sqrt[4]{\frac{162m^{14}}{n^{12}}}$

Responder

$r\sqrt[3]{\frac{40}{s}}$
$\frac{3m^3\sqrt[4]{2m^2}}{∣n^3∣}$

Sumar y restar raíces superiores

Podemos sumar y restar raíces superiores como agregamos y restamos raíces cuadradas. Primero proporcionamos una definición formal de radicales similares.

Definición: COMO RADICALES

Los radicales con el mismo índice y el mismo radicando se llaman radicales similares.

Al igual que los radicales tienen el mismo índice y el mismo radicando.

$9\sqrt[4]{42x}$ y $−2\sqrt[4]{42x}$ son como radicales.
$5\sqrt[3]{125x}$ y no $6\sqrt[3]{125y}$ son como radicales. Los radicandos son diferentes.
$2\sqrt[5]{1000q}$ y no $−4\sqrt[4]{1000q}$ son como radicales. Los índices son diferentes.

Sumamos y restamos como radicales de la misma manera que sumamos y restamos términos similares. Podemos agregar $9\sqrt[4]{42x}+(−2\sqrt[4]{42x})$ y el resultado es $7\sqrt[4]{42x}$ .

Ejemplo $\PageIndex{37}$

Simplificar:

$\sqrt[3]{4x}+\sqrt[3]{4x}$
$4\sqrt[4]{8}−2\sqrt[4]{8}$

Responder

1.	$\sqrt[3]{4x}+\sqrt[3]{4x}$
Los radicales son como, entonces sumamos los coeficientes	$2\sqrt[3]{4x}$
2.	$4\sqrt[4]{8}−2\sqrt[4]{8}$
Los radicales son como, así restamos los coeficientes.	$2\sqrt[4]{8}$

Ejemplo $\PageIndex{38}$

Simplificar:

$\sqrt[5]{3x}+\sqrt[5]{3x}$
$3\sqrt[3]{9}−\sqrt[3]{9}$

Responder

$2\sqrt[5]{3x}$
$2\sqrt[3]{9}$

Ejemplo $\PageIndex{39}$

Simplificar:

$\sqrt[4]{10y}+\sqrt[4]{10y}$
$5\sqrt[6]{32}−3\sqrt[6]{32}$ .

Responder

$2\sqrt[4]{10y}$
$2\sqrt[6]{32}$

Cuando una expresión no parece tener como radicales, primero simplificaremos cada radical. A veces esto lleva a una expresión con radicales similares.

Ejemplo $\PageIndex{40}$

Simplificar:

$\sqrt[3]{54}−\sqrt[3]{16}$
$\sqrt[4]{48}+\sqrt[4]{243}$ .

Responder

1.	$\sqrt[3]{54}−\sqrt[3]{16}$
Reescribe cada radicando usando factores de cubo perfectos.	$\sqrt[3]{27}·\sqrt[3]{2}−\sqrt[3]{8}·\sqrt[3]{2}$
Reescribe los cubos perfectos.	$\sqrt[3]{(3)^3}·\sqrt[3]{2}−\sqrt[3]{(2)^3}·\sqrt[3]{2}$
Simplifica los radicales cuando sea posible.	$3\sqrt[3]{2}−2\sqrt[3]{2}$
Combina como radicales.	$\sqrt[3]{2}$
2.	$\sqrt[4]{48}+\sqrt[4]{243}$
Reescribir usando cuatro factores de potencia perfectos.	$\sqrt[4]{16}·\sqrt[4]{3}+\sqrt[4]{81}·\sqrt[4]{3}$
Reescribe cada radicando como un producto usando factores de cubo perfectos.	$\sqrt[4]{(2)^4}·\sqrt[4]{3}+\sqrt[4]{(3)^4}·\sqrt[4]{3}$
Reescribe el numerador como producto de dos radicales.	$2\sqrt[4]{3}+3\sqrt[4]{3}$
Simplificar.	$5\sqrt[4]{3}$

Ejemplo $\PageIndex{41}$

Simplificar:

$\sqrt[3]{192}−\sqrt[3]{81}$
$\sqrt[4]{32}+\sqrt[4]{512}$ .

Contestar

$\sqrt[3]{3}$
$6\sqrt[4]{2}$

Ejemplo $\PageIndex{42}$

Simplificar:

$\sqrt[3]{108}−\sqrt[3]{250}$
$\sqrt[5]{64}+\sqrt[5]{486}$ .

Contestar

$−\sqrt[3]{2}$
$5\sqrt[5]{2}$

Ejemplo $\PageIndex{43}$

Simplificar:

$\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}$
$\sqrt[4]{162y^9}+\sqrt[4]{512y^5}$ .

Contestar

1.	$\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}$
Reescribe cada radicando usando factores de cubo perfectos.	$\sqrt[3]{8x^3}·\sqrt[3]{3x}−\sqrt[3]{−27x^6}·\sqrt[3]{3x}$
Reescribe los cubos perfectos.	$\sqrt[3]{(2x)^3}·\sqrt[3]{3x}−\sqrt[3]{(−3x^2)^3}·\sqrt[3]{3x}$
Simplifica los radicales cuando sea posible.	$2x\sqrt[3]{3x}−(−3x^2\sqrt[3]{3x})$
2.	$\sqrt[4]{162y^9}+\sqrt[4]{516y^5}$
Reescribir usando cuatro factores de potencia perfectos.	$\sqrt[4]{81y^8}·\sqrt[4]{2y}+\sqrt[4]{256y^4}·\sqrt[4]{2y}$
Reescribe cada radicando como un producto usando factores de cubo perfectos.	$\sqrt[4]{(3y^2)^4}·\sqrt[4]{2y}+\sqrt[4]{(4y)^4}·\sqrt[4]{2y}$
Reescribe el numerador como producto de dos radicales.	$3y^2\sqrt[4]{2y}+4\|y\|\sqrt[4]{2y}$

Ejemplo $\PageIndex{44}$

Simplificar:

$\sqrt[3]{32y^5}−\sqrt[3]{−108y^8}$
$\sqrt[4]{243r^{11}}+\sqrt[4]{768r^{10}}$ .

Contestar

$2y\sqrt[3]{4y^2}+3y^2\sqrt[3]{4y^2}$
$3r^2\sqrt[4]{3r^3}+4r^2\sqrt[4]{3r^2}$

Ejemplo $\PageIndex{45}$

Simplificar:

$\sqrt[3]{40z^7}−\sqrt[3]{−135z^4}$
$\sqrt[4]{80s^{13}}+\sqrt[4]{1280s^6}$ .

Contestar

$2z^2\sqrt[3]{5z}+3z^5\sqrt[3]{5z}$
$2∣s^3∣\sqrt[4]{5s}+4|s|\sqrt[4]{5s}$

Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con la simplificación de las raíces superiores.

Simplificar las raíces superiores
Sumar/restar raíces con índices más altos

Conceptos clave

Propiedades de
$\sqrt[n]{a}$ cuando n es un número par y
- $a \ge 0$ , entonces $\sqrt[n]{a}$ es un número real
- $a < 0$ , entonces no $\sqrt[n]{a}$ es un número real
- Cuando n es un número impar, $\sqrt[n]{a}$ es un número real para todos los valores de a.
- Para cualquier entero $n \ge 2$ , cuando n es impar $\sqrt[n]{a^n}=a$
- Para cualquier entero $n \ge 2$ , cuando n es par $\sqrt[n]{a^n}=|a|$
$\sqrt[n]{a}$ se considera simplificado si a no tiene factores de $m^n$ .
$\sqrt[n]{ab}=\sqrt[n]{a}·\sqrt[n]{b}$ y $\sqrt[n]{a}·\sqrt[n]{b}=\sqrt[n]{ab}$
$\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$ y $\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}$
Para combinar como radicales, simplemente sumar o restar los coeficientes manteniendo el radical igual.

Glosario

n th raíz de un número: Si $b^n=a$ , entonces b es una raíz n th de a.

raíz principal n th: La raíz principal n th de a está escrita $\sqrt[n]{a}$ .

índice: $\sqrt[n]{a}$ n se llama el índice del radical.

como radicales: Los radicales con el mismo índice y el mismo radicando se llaman radicales similares.

Objetivos de aprendizaje

Nota

Simplifique las expresiones con raíces superiores

Definición: N TH RAÍZ DE UN NÚMERO

Definición: PROPIEDADES DEn√a\sqrt[n]{a}

Ejemplo9.7.1\PageIndex{1}

Ejemplo9.7.2\PageIndex{2}

Ejemplo9.7.3\PageIndex{3}

Ejemplo9.7.4\PageIndex{4}

Ejemplo9.7.5\PageIndex{5}

Ejemplo9.7.6\PageIndex{6}

Definición: SIMPLIFICACIÓN DE RAÍCES PARES Y

Ejemplo9.7.7\PageIndex{7}

Ejemplo9.7.8\PageIndex{8}

Ejemplo9.7.9\PageIndex{9}

Ejemplo9.7.10\PageIndex{10}

Ejemplo9.7.11\PageIndex{11}

Ejemplo9.7.12\PageIndex{12}

Ejemplo9.7.13\PageIndex{13}

Ejemplo9.7.14\PageIndex{14}

Ejemplo9.7.15\PageIndex{15}

Utilice la propiedad Product para simplificar expresiones con raíces más altas

Definición: RAÍZ SIMPLIFICADA

Definición: PROPIEDAD DE PRODUCTO DE N TH ROOTS

Ejemplo9.7.16\PageIndex{16}

Ejemplo9.7.17\PageIndex{17}

Ejemplo9.7.18\PageIndex{18}

Ejemplo9.7.19\PageIndex{19}

Ejemplo9.7.20\PageIndex{20}

Ejemplo9.7.21\PageIndex{21}

Ejemplo9.7.22\PageIndex{22}

Ejemplo9.7.23\PageIndex{23}

Ejemplo9.7.24\PageIndex{24}

Ejemplo9.7.25\PageIndex{25}

Ejemplo9.7.26\PageIndex{26}

Ejemplo9.7.27\PageIndex{27}

Utilice la propiedad Cocient para simplificar expresiones con raíces más altas

Ejemplo9.7.28\PageIndex{28}

Ejemplo9.7.29\PageIndex{29}

Ejemplo9.7.30\PageIndex{30}

Definición: PROPIEDAD COCIENTE DE LAS RAÍCES N TH

Ejercicio9.7.31\PageIndex{31}

Ejemplo9.7.32\PageIndex{32}

Ejemplo9.7.33\PageIndex{33}

Ejemplo9.7.34\PageIndex{34}

Ejemplo9.7.35\PageIndex{35}

Ejemplo9.7.36\PageIndex{36}

Sumar y restar raíces superiores

Definición: COMO RADICALES

Ejemplo9.7.37\PageIndex{37}

Ejemplo9.7.38\PageIndex{38}

Ejemplo9.7.39\PageIndex{39}

Ejemplo9.7.40\PageIndex{40}

Ejemplo9.7.41\PageIndex{41}

Ejemplo9.7.42\PageIndex{42}

Ejemplo9.7.43\PageIndex{43}

Ejemplo9.7.44\PageIndex{44}

Ejemplo9.7.45\PageIndex{45}

Conceptos clave

Glosario

Support Center

How can we help?

Definición: PROPIEDADES DE $\sqrt[n]{a}$

Ejemplo $\PageIndex{1}$

Ejemplo $\PageIndex{2}$

Ejemplo $\PageIndex{3}$

Ejemplo $\PageIndex{4}$

Ejemplo $\PageIndex{5}$

Ejemplo $\PageIndex{6}$

Ejemplo $\PageIndex{7}$

Ejemplo $\PageIndex{8}$

Ejemplo $\PageIndex{9}$

Ejemplo $\PageIndex{10}$

Ejemplo $\PageIndex{11}$

Ejemplo $\PageIndex{12}$

Ejemplo $\PageIndex{13}$

Ejemplo $\PageIndex{14}$

Ejemplo $\PageIndex{15}$

Ejemplo $\PageIndex{16}$

Ejemplo $\PageIndex{17}$

Ejemplo $\PageIndex{18}$

Ejemplo $\PageIndex{19}$

Ejemplo $\PageIndex{20}$

Ejemplo $\PageIndex{21}$

Ejemplo $\PageIndex{22}$

Ejemplo $\PageIndex{23}$

Ejemplo $\PageIndex{24}$

Ejemplo $\PageIndex{25}$

Ejemplo $\PageIndex{26}$

Ejemplo $\PageIndex{27}$

Ejemplo $\PageIndex{28}$

Ejemplo $\PageIndex{29}$

Ejemplo $\PageIndex{30}$

Ejercicio $\PageIndex{31}$

Ejemplo $\PageIndex{32}$

Ejemplo $\PageIndex{33}$

Ejemplo $\PageIndex{34}$

Ejemplo $\PageIndex{35}$

Ejemplo $\PageIndex{36}$

Ejemplo $\PageIndex{37}$

Ejemplo $\PageIndex{38}$

Ejemplo $\PageIndex{39}$

Ejemplo $\PageIndex{40}$

Ejemplo $\PageIndex{41}$

Ejemplo $\PageIndex{42}$

Ejemplo $\PageIndex{43}$

Ejemplo $\PageIndex{44}$

Ejemplo $\PageIndex{45}$