4.8: Funciones inversas

Última actualización
Guardar como PDF

Page ID: 111946

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Una función inversa deshace la acción de la función original. Entonces, la inversa de una función que cuadraba un número sería una función que enraizó un número cuadrado. En general, una función inversa tomará un$y$ valor de la función original y devolverá el$x$ valor que la produjo.

Esto lo podemos ver en una aplicación. Dado un objeto con poca o ninguna resistencia al aire del que se cae$100 \mathrm{ft}$, la función que describe su altura en función del tiempo sería:
\ [
H (t) =100-16 t^ {2}
\]
En esta función,$H(t)$ es la altura del objeto en el momento $t .$Si quisiéramos darle la vuelta a esto para que describiera el tiempo para una altura dada, entonces querríamos aislar la$t$ variable. En este ejemplo, la gráfica de la función cambiaría en que la variable independiente original -$t,$ se convierte en la variable dependiente en la función inversa.
\ [
\ begin {alineado}
h &=100-16 t^ {2}\\
16 t^ {2} &=100-h\\
t^ {2} &=\ frac {100-h} {16}\\
t &=\ sqrt {\ frac {100-h} {16}}\
T (h) &=\ frac {\ sqrt {100-h}} {4}
\ final {alineado}
\]

Función original: Función$H(t)=100-16 t^{2}$
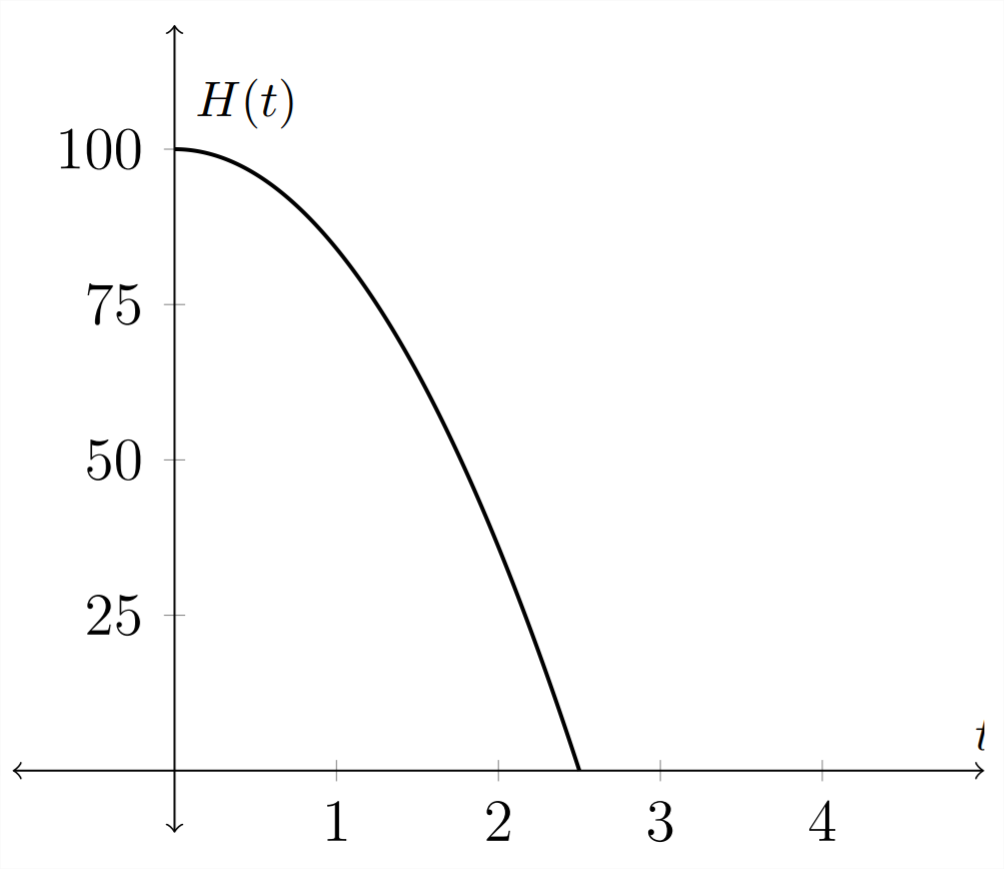
$clipboard_e3860268f9d6975d40696f81c10a4e402.png$
inversa:$T(h)=\frac{\sqrt{100-h}}{4}$
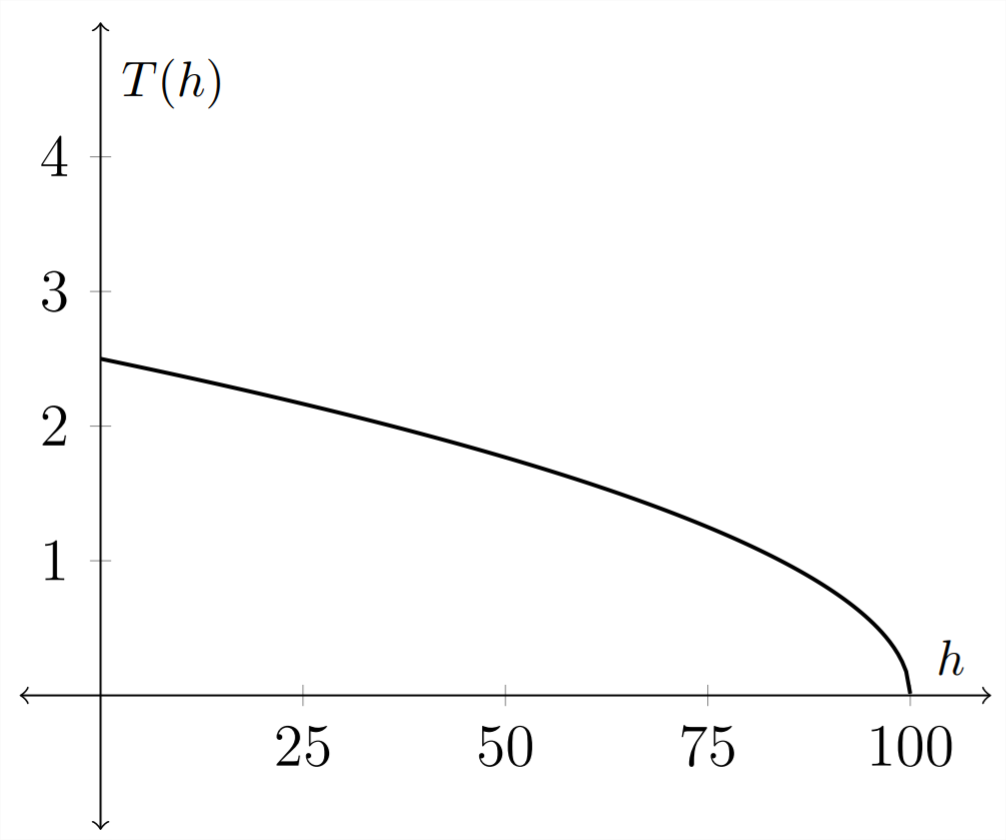
$clipboard_e89256480f8675d2b57ce0801450f241e.png$
Observe que la gráfica de la función inversa es la función original reflejada sobre la línea$y=x,$ porque una función inversa intercambia la función independiente y variables dependientes.

Encontrar una fórmula para una función inversa puede ser más confuso cuando consideramos una función estándar$y=f(x) .$ En nuestra notación estándar, siempre se considera que$x$ es la variable independiente y siempre se considera que$y$ es la variable dependiente.

Observe en el ejemplo anterior que cuando graficamos la función y su inversa, la etiqueta en el$x$ eje cambió de$t$ a$h .$ En una función estándar, el$x$ eje siempre será el$x$ eje y el$y$ eje siempre será el$y$ eje. Para compensar esto, cuando encontramos una función inversa para una función establecida en términos de$x$ y generalmente$y$ intercambiamos los$y$ términos$x$ y para que$x$ quede la variable independiente.
En nuestro ejemplo, teníamos
\ [
H (t) =100-16 t^ {2}
\]
y encontramos que la inversa era
\ [
T (h) =\ frac {\ sqrt {100-h}} {4}
\]
Si la función original hubiera sido expresada en términos de $x$y$y,$ entonces el proceso se habría visto así:
\ begin {aligned}
f (x) &=100-16 x^ {2}\\
y &=100-16 x^ {2}\\
16 x^ {2} &=100-y\
x^ {2} &=\ frac {100-y} {16}\\
x &=\ sqrt {\ frac {100-y} {16}}\\
x &=\ frac {\ sqrt {100-y}} {4}
\ end {alineadas}

Luego cambiamos$y$ las variables$x$ y para mantener la$x$ como la variable independiente:
\ [
y=f^ {-1} (x) =\ frac {\ sqrt {100-x}} {4}
\]
$\mathrm{So}$
\ [
f (x) =100-16 x^ {2}
\]
y
\ [
f^ {-1} (x) =\ frac {\ sqrt {100-x}} {4}
\]

Ejercicios 4.8
Dada la función$f(x),$ encontrar la función inversa$f^{-1}(x)$
1)$\quad f(x)=3 x$
2)$\quad f(x)=-4 x$
3)$\quad f(x)=4 x+2$
4)$\quad f(x)=1-3 x$
5)$\quad f(x)=x^{3}-1$
6)$\quad f(x)=x^{3}+1$
7)$\quad f(x)=x^{2}+4 (x \geq 4)$
8)$\quad f(x)=x^{2}+9 (x \geq 9)$
9)$\quad f(x)=\frac{4}{x}$
10)$\quad f(x)=-\frac{3}{x}$
11)$\quad f(x)=\frac{1}{x-2}$
12)$\quad f(x)=\frac{4}{x+2}$
13)$\quad f(x)=\frac{2}{x+3}$
14)$\quad f(x)=\frac{4}{2-x}$
15)$\quad f(x)=\frac{3 x}{x+2}$
16) $\quad f(x)=-\frac{2 x}{x-1}$
17)$\quad f(x)=\frac{2 x}{3 x-1}$
18)$\quad f(x)=-\frac{3 x+1}{x}$
19)$\quad f(x)=\frac{3 x+4}{2 x-3}$
20)$\quad f(x)=\frac{2 x-3}{x+4}$
21)$\quad f(x)=\frac{2 x+3}{x+2}$
22)$\quad f(x)=-\frac{3 x+4}{x-2}$
Encuentra la función inversa para cada una de las siguientes aplicaciones.
23) El volumen de agua que queda en un tanque de 1000 galones que drena en 40 minutos es modelado por la ecuación:
\ [
V (t) =1000\ left (1-\ frac {t} {40}\ right) ^ {2}
\]
Find$T(v)$ - la función que te dice cuánto tiempo ha estado el agua drenaje dado un volumen particular que queda en el tanque. El tiempo se mide en minutos y el volumen se mide en galones.
24) La velocidad de un vehículo en millas por hora que deja marcas de derrape$d$ pies de largo es modelada por la ecuación:
\ [
R (d) =2\ sqrt {5 d}
\]
Find$D(r)$ - la función que le indica la distancia de parada para un vehículo viajando$r$ millas por hora.
25) El periodo de un péndulo de longitud$\ell$ puede ser expresado por la relación:
\ [
T (\ ell) =2\ pi\ sqrt {\ frac {\ ell} {980}}
\]
Encuentra la función$L(t)$ que determina la longitud de un péndulo dado su periodo. Aquí el tiempo se mide en segundos y la longitud se mide en centímetros.
26) El volumen de una esfera de radio$r$ viene dado por la fórmula:
\ [
V (r) =\ frac {4} {3}\ pi r^ {3}
\]
Find$R(v)$ - la función que determina el radio de una esfera dado su volumen.