8.5: Más aplicaciones
- Page ID
- 111978
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)1.5 Más Aplicaciones
A veces resolver problemas que involucran triángulos rectos requiere el uso de un sistema de ecuaciones. Un método común para determinar la altura de un objeto cuya base es inaccesible es el de medir el ángulo de elevación desde dos lugares diferentes frente al objeto. Si mide el ángulo de elevación a la parte superior de una antena de radio como 74, luego camina hacia atrás 50 pies y mide el ángulo de elevación hasta la parte superior de la antena como 61 ', entonces tendríamos algo como el diagrama a continuación:
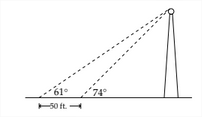
Una de las primeras cosas que podemos hacer es introducir algunas etiquetas para las distancias desconocidas:
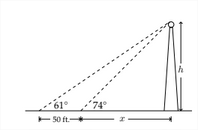
Entonces, podemos decir que:
\(\tan 74^{\circ}=\frac{h}{x}\)
\(\tan 61^{\circ}=\frac{h}{x+50}\)
Para resolver este sistema de ecuaciones, estableceremos la primera igual a\(h:\)
\ [
\ begin {array} {c}
\ tan 74^ {\ circ} =\ frac {h} {x}\\
x *\ tan 74^ {\ circ} =h
\ end {array}
\]
Luego, sustituya esto en la segunda ecuación:
\ [
\ tan 61^ {\ circ} =\ frac {h} {x+30}
\]
\ [
\ tan 61^ {\ circ} =\ frac {x\ tan 74^ {\ circ}} {x+50}
\]
Multiplicar en ambos lados por\(x+50:\)
\((x+50) \tan 61^{\circ}=\frac{x \tan 74^{\circ}}{x+30}(x+50)\)
\((x+50) \tan 61^{\circ}=x \tan 74^{\circ}\)
Hay dos opciones para resolver esta ecuación - podemos aferrarnos a las tangentes
tal como son y resolver para\(x\) en términos\(\tan 74^{\circ}\) y\(\tan 61^{\circ},\) o podemos aproximarnos\(\tan 74^{\circ}\) y\(\tan 61^{\circ}\) y generar un valor aproximado para\(x\) y\(h .\) Primero vamos a aproximar:
\((x+50) \tan 61^{\circ}=x \tan 74^{\circ}\)
\ [
(x+50) * 1 .804\ aprox 3.4874 x
\]
\(1.804 x+90.2024 \approx 3.4874 x\)
\(90.2024 \approx 1.6834 x\)
\ [
53.58\ approx x
\]
\(x * \tan 74^{\circ}=h\)
\ [
\ begin {array} {c}
53.58 *\ tan 74^ {\ circ}\ approx h\\
186.87\ text {pies}\ approx h
\ end {array}
\]
El otro método es un poco complicado algebraicamente:
\ [
(x+50)\ tan 61^ {\ circ} =x\ tan 74^ {\ circ}
\]
\ [
\ comenzar {matriz} {l}
x\ tan 61^ {\ circ} +50\ tan 61^ {\ circ} =x\ tan 74^ {\ circ}\
50\ tan 61^ {\ circ} =x bronceado\ 74^ {\ circ} -x\ tan 61^ {\ circ}\\
50\ tan 61^ {\ circ} =x\ izquierda (\ tan 74^ {\ circ} -\ tan 61^ {\ circ}\ derecha)\\
\ frac {50\ tan 61^ {\ circ}} {\ left (\ tan 74^ {\ circ} -\ tan 61^ {\ circ}\ derecha)} =x
\ end {array}
\]
En este punto, puedes aproximar el valor de\(x\) y resolver para\(h\), o expresar el valor de\(h\) exactamente como
\ [
\ tan 74^ {\ circ} *\ frac {50\ tan 61^ {\ circ}} {\ circ} {\ izquierda (\ tan 74^ {\ circ} -\ tan 61^ {\ circ}\ derecha)} =h
\]
Ejercicios 1.5
1. Encuentra la altura indicada\(h\)
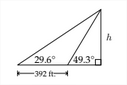
2. Encuentra la altura indicada\(h\)
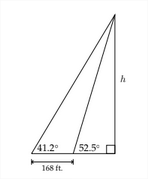
3. Un pequeño avión que vuela a una altitud de 5300 pies mira dos autos frente al avión viajando en una carretera directamente debajo de él. El ángulo de depresión con respecto al automóvil más cercano es\(62^{\circ}\) y el ángulo de depresión con respecto al automóvil más distante es\(41^{\circ}\). ¿A qué distancia están los autos?
4. Un globo aerostático está volando por encima de una carretera recta. Para estimar su altitud, las personas en el globo miden los ángulos de depresión a dos marcadores de millas consecutivas en el mismo lado del globo. El ángulo al marcador dosificador es\(17^{\circ}\) y el ángulo hacia el más lejano está ¿\(13^{\circ} .\)A qué altitud vuela el globo?
5. Para estimar la altura de una montaña, se mide el ángulo de elevación desde un punto
en terreno llano hasta la cima de la montaña para ser\(32^{\circ} .\) Desde un punto
1000 pies más cerca de la montaña, el ángulo de elevación se mide para ser\(35^{\circ}\) ¿Qué tan alto es el monte sobre el suelo desde el que se tomaron las medidas?
6. El ángulo de elevación desde un punto en el suelo hasta la parte superior de una pirámide es\(35^{\circ} 30^{\prime} .\) El ángulo de elevación desde un punto 135 pies más atrás hasta la parte superior de la pirámide es\(21^{\circ} 10\). ¿Cuál es la altura de la pirámide?
7. Un observador en un faro a 70 pies sobre el nivel del mar mira el ángulo de depresión de un barco que se aproxima para ser\(15^{\circ} 50^{\prime} .\) Unos minutos después el ángulo de depresión es avistado en\(35^{\circ} 40^{\prime} .\) Encuentra la distancia recorrida por el barco durante ese tiempo.
8. Para estimar la altura de un árbol, un silvicultor se encuentra al oeste del árbol y otro forestal se levanta al norte del árbol. Los dos silvicultores están a la misma distancia de la base del árbol y están a 45 pies uno del otro. Si el ángulo de elevación para cada silvicultor es\(40^{\circ},\) ¿qué tan alto es el árbol?
9. Un barco está anclado en una larga costa recta que corre de este a oeste. De dos puntos de observación ubicados a 10 millas de distancia en la costa, los rodamientos del barco desde cada punto de observación están\(S 35^{\circ} E\) y\(S 17^{\circ} W .\) ¿A qué distancia de la costa está el barco?
10. Desde vigilancia de incendios Estación Alfa el porte de un incendio forestal es\(N 52^{\circ} E .\) Desde el mirador Estación Beta, ubicada a 6 millas por el este de la Estación Alfa, el rumbo está\(N 38^{\circ} \mathrm{W}\) ¿A qué distancia está el incendio de la Estación Alfa?
11. Desde un punto a 200 pies de la base de una iglesia, el ángulo de elevación a la parte superior del campanario es\(28^{\circ},\) mientras que el ángulo de elevación al fondo del campanario es\(20^{\circ} .\) ¿Qué tan alto del suelo es la parte superior del campanario?
12. Una torre de televisión de 75 pies de altura está instalada en la parte superior de un edificio. Desde un punto en el suelo frente al edificio, el ángulo de elevación a la parte superior de la torre es\(62^{\circ}\) y el ángulo de elevación al fondo de la torre es\(44^{\circ} .\) ¿Qué tan alto es el edificio?