10.2: Identidades de doble ángulo
- Page ID
- 112034
En esta sección incluiremos varias identidades nuevas a la colección que establecimos en la sección anterior. Estas nuevas identidades se denominan “Identidades de Doble Ángulo\(^{\prime \prime}\) porque normalmente tratan de relaciones entre funciones trigonométricas de un ángulo particular y funciones de “dos veces” o el doble del ángulo original.
Para establecer la validez de estas identidades necesitamos usar lo que se conoce como las Identidades Suma y Diferencia. Estas son identidades que tratan con expresiones como\(\sin (\alpha+\beta) .\) Primero estableceremos una expresión que es equivalente a\(\cos (\alpha-\beta)\)
Empecemos con el círculo unitario:
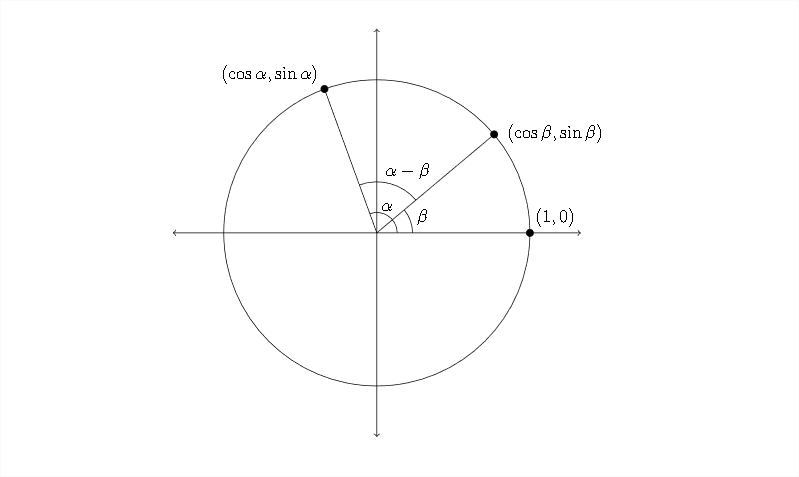
Si giramos todo en esta imagen en sentido horario para que el punto\((\cos \beta, \sin \beta)\) etiquetado se desplace hacia abajo hasta el punto etiquetado\((1,0),\) entonces el ángulo de rotación en el diagrama será\(\alpha-\beta\) y el punto correspondiente en el borde del círculo será:
\((\cos (\alpha-\beta), \sin (\alpha-\beta))\)
El diagrama que representa esta rotación está en la página siguiente.
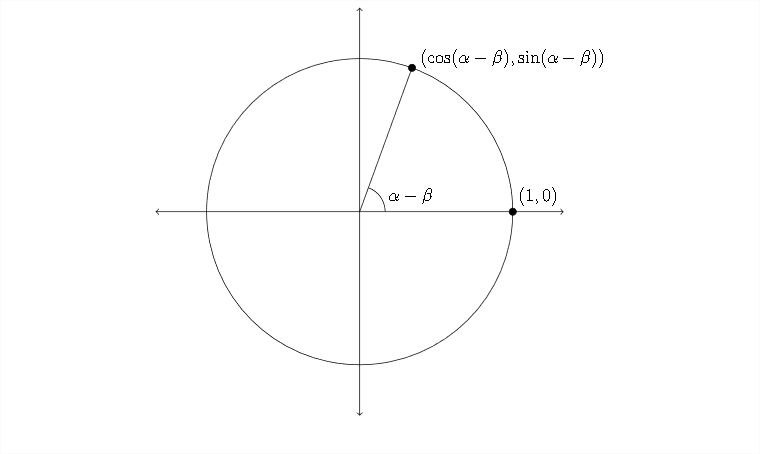
ya que el segundo diagrama se crea girando las líneas y puntos del primer diagrama, la distancia entre los puntos\((\cos \alpha, \sin \alpha)\) y\((\cos \beta, \sin \beta)\) en el primer diagrama es la misma que la distancia entre\((\cos (\alpha-\beta), \sin (\alpha-\beta))\) y el punto (1,0) en el segundo diagrama.
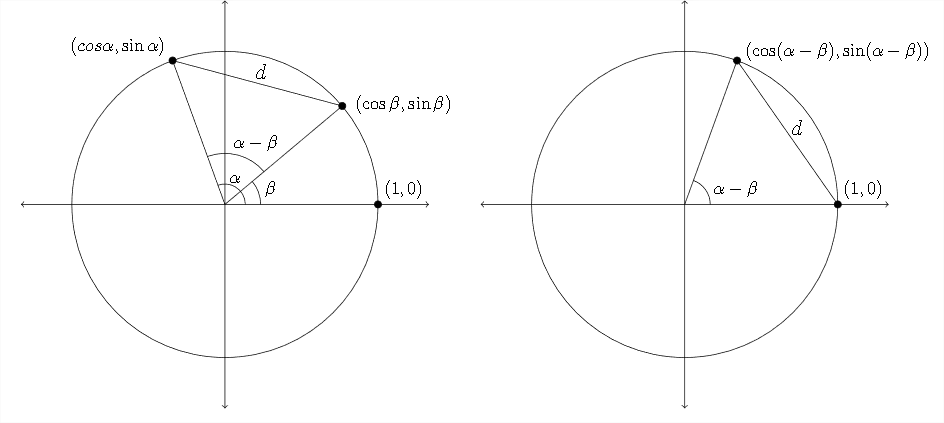
En el diagrama de arriba la longitud de\(d\) en cada imagen es la misma.
Podemos representar esta distancia\(d\) con la fórmula de distancia utilizada para calcular la distancia entre dos puntos en el plano de coordenadas:
La distancia entre los puntos\(\left(x_{1}, y_{1}\right)\) y\(\left(x_{2}, y_{2}\right)\) es
\ [
d=\ sqrt {\ left (x_ {2} -x_ {1}\ right) ^ {2} +\ left (y_ {2} -y_ {1}\ right) ^ {2}}
\]
Entonces, en el primer diagrama la distancia\(d\) será:
\ [
d=\ sqrt {(\ cos\ alpha-\ cos\ beta) ^ {2} + (\ sin\ alpha-\ sin\ beta) ^ {2}}
\]
En el segundo diagrama la distancia\(d\) será:
\ [
d=\ sqrt {(\ cos (\ alpha-\ beta) -1) ^ {2} + (\ sin (\ alpha-\ beta) -0) ^ {2}}
\]
ya que estas distancias son las mismas, podemos establecerlas iguales entre sí:
\ [
\ sqrt {(\ cos\ alpha-\ cos\ beta) ^ {2} + (\ sin\ alfa-\ sin\ beta) ^ {2}} =\ sqrt {(\ cos (\ alpha-\ beta) -1) ^ {2} + (\ sin (\ alpha-\ beta) -0) ^ {2}}
\]
Cuadraremos ambos lados para despejar los radicales:
\ [
(\ cos\ alpha-\ cos\ beta) ^ {2} + (\ sin\ alpha-\ sin\ beta) ^ {2} =(\ cos (\ alpha-\ beta) -1) ^ {2} + (\ sin (\ alpha-\ beta) -0) ^ {2}
\]
A continuación, vamos a reescribir\((\sin (\alpha-\beta)-0)^{2}\) como\(\sin ^{2}(\alpha-\beta)\)
\ [
(\ cos\ alfa-\ cos\ beta) ^ {2} + (\ sin\ alfa-\ sin\ beta) ^ {2} =(\ cos (\ alfa-\ beta) -1) ^ {2} +\ sin ^ {2} (\ alfa-\ beta)
\]
Ahora trabajaremos para simplificar las expresiones del lado izquierdo de esta ecuación.
\ [
(\ cos\ alpha-\ cos\ beta) ^ {2} + (\ sin\ alpha-\ sin\ beta) ^ {2} =(\ cos (\ alpha-\ beta) -1) ^ {2} +\ sin ^ {2} (\ alpha-\ beta)
\]
Primero, cada uno necesita ser cuadrado:
\ [\ begin {array} {l}
(
\ cos\ alpha-\ cos\ cos\ cos\\ beta) ^ {2} =\ cos ^ {2}\ alfa-2\ cos\ alfa\ cos\ cos\ beta+\ cos ^ {2}\ beta\\
(\ sin\ alfa-\ sin\ beta) ^ {2} =\ sin ^ {2}\ alpha-2\ sin\ alpha\ sin\ beta+\ sin ^ {2}\ beta
\ end {array}
\]
Entonces, el lado izquierdo será ahora:
\ [\ cos ^ {2}
\ alpha-2\ cos\ alpha\ cos\ alpha\ cos\ beta+ cos\ {2}\ beta+\ sin ^ {2}\ alfa-2\ sin \ alfa\ sin\ beta+\ sin ^ {2}\ beta
\]
Si reorganizamos esto un poco, se simplificará muy bien:
\ [
\ begin {array} {l}
\ cos ^ {2}\ alpha-2\ cos\ alpha\ cos\ beta+\ cos ^ {2}\ beta+\ sin ^ {2}\ alpha-2\ sin\ alpha\ sin\ beta+\ sin ^ {2}\ beta\\ sin ^ {2}
\ alpha+\ cos ^ {2}\ alfa+\ cos ^ {2}\ alfa+\ sin ^ {2}\ beta+\ cos ^ {2}\ beta-2\ cos\ alpha\ cos\ beta-2\ sin\ alpha\ sin\ beta
\ end {array}
\]
Observe las identidades pitagóricas al frente de esta expresión - estas son cada una igual a 1:
\ [
\ begin {array} {c}
\ sin ^ {2}\ alpha+\ cos ^ {2}\ alpha+\ sin ^ {2}\ beta+\ cos ^ {2}\ beta-2\ cos\ alfa\ cos\ beta-2\ sin\ alfa\ sin\ beta\\
1+1-2\ cos\ alfa\ cos\ beta-2\ sin\ alfa\ sin\ alfa\ sin\ beta\
2-2\ cos\ alfa\ cos\ beta-2\ sin\ alfa\ sin\ beta\\
2 (1-\ cos\ alfa\ cos\ beta-\ sin\ alfa\ sin\ beta)
\ end {array}
\]
Ahora que hemos simplificado el lado izquierdo, simplificaremos el lado derecho Primero cuadraremos la expresión\((\cos (\alpha-\beta)-1)^{2}\)
\ [
(\ cos (\ alpha-\ beta) -1) ^ {2} =\ cos ^ {2} (\ alpha-\ beta) -2\ cos (\ alpha-\ beta) +1
\]
Entonces, el lado derecho es ahora:
\ [
\ cos ^ {2} (\ alpha-\ beta) -2\ cos (\ alpha-\ beta) +1+\ sin ^ {2} (\ alpha-\ beta)
\]
Si reorganizamos esta expresión, volveremos a tener una bonita Identidad Pitagórica:
\ [
\ begin {array} {c}
\ sin ^ {2} (\ alpha-\ beta) +\ cos ^ {2} (\ alpha-\ beta) -2\ cos (alfa \-\ beta) +1\\
1-2\ cos (\ alfa-\ beta) +1\\
2-2\ cos (\ alfa-\ beta)\\
2 (1-\ cos (\ alfa-\ beta))
\ end {array}
\]
Entonces el lado izquierdo era igual a:
\ [
2 (1-\ cos\ alpha\ cos\ beta-\ sin\ alpha\ sin\ beta)
\]
Y el lado derecho era igual a:
\ [
2 (1-\ cos (\ alpha-\ beta))
\]
Entonces, nuestra declaración original en forma simplificada es:
\ [
2 (1- \ cos\ alfa\ cos\ beta-\ sin\ alfa\ sin\ beta) =2 (1-\ cos (\ alfa-\ beta))
\]
Si dividimos por 2 en ambos lados, tendremos:
\ [
1-\ cos\ alfa\ cos\ beta-\ sin\ alfa\ sin\ beta=1-\ cos (\ alpha-\ beta)\]
luego restar 1
\ [
-\ cos
\ alpha\ cos\ alpha\ cos\ beta-\ sin\ alpha\ sin\ alpha\ sin\ beta=-\ cos (\ alpha-\ beta)
\]
y multiplicamos por -1
\ [
\ begin {array} {r}
\ cos\ alpha\ cos\ beta+\ sin\ alpha\ sin\ beta=\ cos (\ alpha-\ beta)\\
\ mathrm {Así},\ cos (\ alpha-\ beta) =\ cos\ alfa\ cos\ beta+\ sin\ alpha\ sin\ beta
\ end {array}
\]
Esto nos ayudará a generar el doble ángulo fórmulas, pero para hacer esto, no queremos\(\cos (\alpha-\beta),\) queremos\(\cos (\alpha+\beta)\) (ya verás por qué en un minuto).
Entonces, para cambiar esto, usaremos identidades para ángulos negativos. Recordemos que en el cuarto cuadrante la función sinusoidal es negativa y la función coseno es positiva. Por ello,\(\sin (-\theta)=-\sin (\theta)\) y\(\cos (-\theta)=\cos (\theta)\)
ahora podemos decir que\(\cos (2 \theta)=\cos (\theta+\theta)=\cos (\theta-(-\theta)) .\) Volviendo a nuestra
identidad porque\(\cos (\alpha-\beta),\) podemos decir que:
\ [
\ comenzar {alineado}
\ cos (\ theta- (-\ theta)) &=\ cos\ theta\ cos (-\ theta) +\ sin\ theta\ sin (-\ theta)\\ cos (
\ theta- (-\ theta)) &=\ cos\ theta\ cos\ theta\ cos\ theta+\ sin\ theta (-\ sin\ theta)
\\ cos (\ theta- (-\ theta)) &=\ cos\ theta\ cos\ theta-\ sin\ theta\ sin\ theta\\
\ cos (\ theta- (-\ theta)) &=\ cos ^ {2}\ theta-\ sin ^ {2}\ theta\
\ cos (\ theta+\ theta) &=\ cos ^ {2}\ theta-\ sin ^ {2}\ theta\
\ cos (2\ theta) &=\ cos ^ {2}\ theta-\ sin ^ {2}\ theta
\ end {alineado}
\]
Este es el doble- identidad del ángulo para el coseno:\(\quad \cos (2 \theta)=\cos ^{2} \theta-\sin ^{2} \theta\)
Esta identidad realmente aparece en cualquiera de las tres formas porque las Identidades Pitágoras se pueden aplicar a esto para cambiar su apariencia:
\ [\ begin {array} {l}
\ cos (2\ theta) =
\ cos ^ {2}\ theta-\ sin ^ {2}\ theta\\ cos (2\ theta) =1-\ sin ^ {2}\ theta-
\ sin ^ {2}\ theta-\ sin ^ {2}\ theta\ sin ^ {2}\ theta\ sin ^ {2}\ theta \\
\ cos (2\ theta) =1-2\ sin ^ {2}\ theta
\ end {array}
\]
Si sustituimos por el\(\sin ^{2} \theta\) término:
\ [
\ begin {array} {l}
\ cos (2\ theta) =\ cos ^ {2}\ theta-\ sin ^ {2}\ theta\
\ cos (2\ theta) =\ cos ^ {2}\ theta-\ izquierda (1-\ cos ^ {2}\ theta\ derecha)\\
\ cos (2\ theta) =\ cos ^ {2}\ theta-1+\ cos ^ {2}\ theta\
\ cos (2\ theta) =2\ cos ^ {2}\ theta-1
\ end {array}
\]
Entonces, las tres formas de la identidad de doble ángulo coseno son:
\ [
\ begin {aligned}
\ cos (2\ theta) &=\ cos ^ {2}\ theta-\ sin ^ {2}\ theta\\
&=2\ cos ^ {2}\ theta-1\\
&=1-2\ sin ^ {2}\ theta
\ end {alineado}
\]
El la identidad de doble ángulo para la función sinusoidal utiliza lo que se conoce como la identidad de cofunción. Recuerda que, en un triángulo rectángulo, el seno de un ángulo es el mismo que el coseno de su complemento (que es el otro ángulo agudo). Esto se debe a que el lado adyacente para un ángulo es el lado opuesto para el otro ángulo. El denominador en ambos casos es la hipotenusa, por lo que las cofunciones de los ángulos complementarios son iguales.
En el siguiente diagrama, podemos ver esto con mayor claridad:
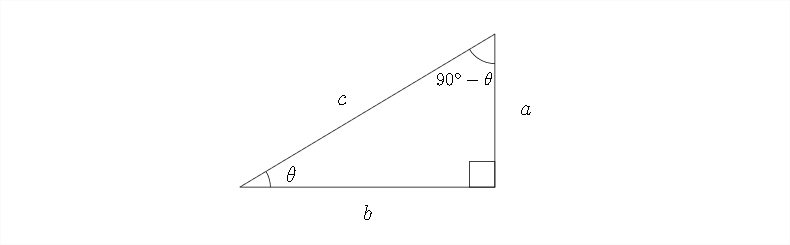
En el diagrama anterior notaremos que:
\ [
\ sin\ theta=\ frac {a} {c} =\ cos\ left (90^ {\ circ} -\ theta\ right)
\]
Entonces, si queremos una identidad para\(\sin (\theta+\theta),\) comenzaremos con lo\(\sin (\alpha+\beta)\) que es equivalente a\(\cos \left(90^{\circ}-(\alpha+\beta)\right) .\) Usaremos un truco aquí y reformularemos esto como:
\ [
\ begin {aligned}
\ sin (\ alpha+\ beta) &=\ cos\ left (90^ {\ circ} - (\ alpha+\ beta)\ right)\\
&=\ cos\ left (90^ {\ circ} -\ alpha-\ beta\ right)\\
&=\ cos\ left (\ left (\ left (90^ {\ circ} -\ alpha\ right) -\ beta\ right)\\
&=\ cos\ izquierda (90^ {\ circ} -\ alfa\ derecha)\ cos\ beta+\ sin\ izquierda (90^ {\ circ} -\ alfa\ derecha)\ sin\ beta\\
&=\ sin\ alfa\ cos\ beta+\ cos\ alfa\ sin\ beta
\ fin {alineado}
\]
Ahora, podemos usar esto para encontrar una expresión para\(\sin 2 \theta=\sin (\theta+\theta)\)
\ [
\ begin {aligned}
\ sin 2\ theta &=\ sin (\ theta+\ theta)\\
&=\ sin\ theta\ cos\ theta+\ cos\ theta\ sin\ theta\
&=2\ sin\ theta\ cos\ theta
\ end {aligned}
\]
Ejercicios 3.2
Aquí hay un resumen de todas las identidades con las que hemos trabajado en este capítulo:
Identidades pitagóricas
\(\sin ^{2} \theta+\cos ^{2} \theta=1\)
\(\tan ^{2} \theta+1=\sec ^{2} \theta\)
\(1+\cot ^{2} \theta=\csc ^{2} \theta\)
Identidades recíprocas
\(\tan \theta=\frac{\sin \theta}{\cos \theta}\)
\(\cot \theta=\frac{\cos \theta}{\sin \theta}\)
\(\sec \theta=\frac{1}{\cos \theta}\)
\(\csc \theta=\frac{1}{\sin \theta}\)
Identidades de doble ángulo
\(\cos (2 \theta)=\cos ^{2} \theta-\sin ^{2} \theta\)
\(\cos (2 \theta)=2 \cos ^{2} \theta-1\)
\(\cos (2 \theta)=1-2 \sin ^{2} \theta\)
\(\sin (2 \theta)=2 \sin \theta \cos \theta\)
Los problemas de trabajo que involucran identidades de doble ángulo son muy similares a las otras identidades con las que hemos trabajado anteriormente, ¡solo tienes más identidades para elegir!
Ejemplo
Verificar la identidad dada:\(\cos 2 x=\frac{1-\tan ^{2} x}{1+\tan ^{2} x}\)
Tenemos tres identidades posibles para elegir para el lado izquierdo, así que esperaremos en eso un momento mientras simplificamos el lado derecho.
\ [
\ begin {alineado}
\ frac {1-\ tan ^ {2} x} {1+\ tan ^ {2} x} &=\ frac {1-\ tan ^ {2} x} {\ seg ^ {2} x}\\
&=\ frac {1} {\ seg ^ {2} x} -\ frac {\ tan ^ {2} x} {\ seg {^ 2}} x}\\
&=\ cos ^ {2} x-\ frac {\ izquierda (\ frac {\ sin ^ {2} x} {\ cos ^ {2} x}\ derecha)} {\ izquierda (\ frac {1} {\ cos ^ {2} x}\ derecha) }\\
&=\ cos ^ {2} x-\ frac {\ sin ^ {2} x} {\ cos ^ {2} x}\ cdot\ frac {\ cos ^ {2} x} {1}\\
&=\ cos ^ {2} x-\ frac {\ sin ^ {2} x} {\ cancel {\ cos ^ {2} x}}\ cdot\ ac {\ cancel {\ cos ^ {2} x}} {1}\\
&=\ cos ^ {2} x-\ sin ^ {2} x
\ end {alineado}
\]
Esta es una de las identidades para\(\cos (2 \theta)\) que podamos detenernos y simplemente declarar\(\cos (2 x)=\)\(\cos ^{2} x-\sin ^{2} x\)
En cada problema verificar la identidad trigonométrica dada.
1. \(\frac{2 \sin x \cos x}{\cos ^{2} x-\sin ^{2} x}=\tan (2 x)\)
2. \(\sec (2 x)=\frac{\sec ^{2} x}{2-\sec ^{2} x}\)
3. \(\sin (2 x) \csc x=2 \cos x\)
4. \(\frac{2 \cos x}{\sin (2 x)}=\csc x\)
5. \(\frac{\cos (2 x)}{\sin x}+\sin x=\frac{\cot x}{\sec x}\)
6. \(\frac{\sin x+\sin (2 x)}{\sec x+2}=\sin x \cos x\)
7. \((\sin x+\cos x)^{2}=1+\sin (2 x)\)
8. \(\left(\sin ^{2} x-1\right)^{2}=\sin ^{4} x+\cos (2 x)\)
9. \(2 \cos x-\frac{\cos (2 x)}{\cos x}=\sec x\)
10. \(\frac{1+\cos (2 x)}{1-\cos (2 x)}=\cot ^{2} x\)
11. \(\frac{\cos (2 x)}{\sin ^{2} x}=\cot ^{2} x-1\)
12. \(\frac{\cos (2 x)}{\sin ^{2} x}=\csc ^{2} x-2\)
13. \(\frac{\cot x-\tan x}{\cot x+\tan x}=\cos 2 x\)
14. \(\sin 2 x=\frac{2(\tan x-\cot x)}{\tan ^{2} x-\cot ^{2} x}\)
15. \(\frac{2 \cos 2 x}{\sin 2 x}=\cot x-\tan x\)
16. \(\tan 2 x=\frac{2}{\cot x-\tan x}\)
17. \(\frac{\sin x}{1+\cos x}+\frac{1+\cos x}{\sin x}=2 \csc x\)
18. \(\tan x+\cot x=2 \csc (2 x)\)
19. \(\cos (2 x)=\frac{\cot ^{2} x-1}{\cot ^{2} x+1}\)
20. \(\sin (2 x)=\frac{2 \tan x}{1+\tan ^{2} x}\)
21. \(\frac{2 \sin ^{2} x}{\sin (2 x)}+\cot x=\sec x \csc x\)
22. \(\sec ^{2} x \cos (2 x)=\sec ^{2} x-2 \tan ^{2} x\)
23. \(\frac{\cos (2 x)}{\sin x}+\sin x=\csc x-\sin x \quad\)
24. \(\frac{2 \tan x-\sin (2 x)}{2 \sin ^{2} x}=\tan x\)


