10.3: Ecuaciones Trigonométricas

Última actualización
Guardar como PDF

Page ID: 112026

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En la sección anterior sobre identidades trigonométricas trabajamos con ecuaciones que serían ciertas para todos los valores de un ángulo particular$\theta .$ Estas son algo así como las ecuaciones algebraicas cuyo conjunto de soluciones es “todos los números reales”, como$2 x+10=$$2(x+1)+8 .$ En esta sección, resolveremos trigonometría ecuaciones cuyo conjunto de soluciones involucra sólo ciertos valores para el ángulo en cuestión. Debido a la naturaleza cíclica de los ángulos con los que estamos trabajando, a menudo habrá un número infinito de soluciones aunque no “todos los números reales”.

Ejemplo 1
He aquí un ejemplo. Supongamos que consideramos la ecuación$\sin x=0.5 .$ Ya sea que usemos tecnología, una tabla o razonamiento para resolver esta ecuación, está claro que una solución es$30^{\circ} .$ Sin embargo, recuerde desde el inicio del Capítulo 2 que la función sinusoidal es positiva en el Cuadrante$\Pi$. Eso significa que un segundo ángulo de cuadrante con un ángulo de referencia de$30^{\circ}$ también tiene un seno igual a$0.5 .$ Recordar el diagrama ASTC del Capítulo 2:

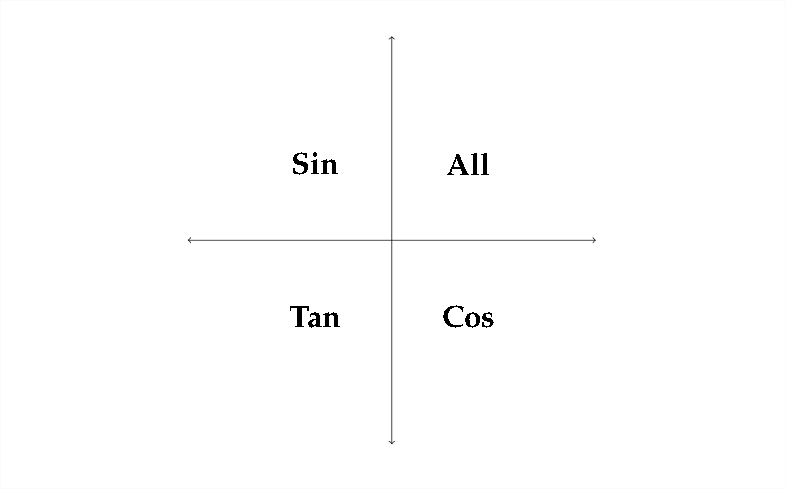
$clipboard_eda8c819a514c82f530fb51f83e24715c.png$

Entonces, la función sinusoidal es positiva en los Cuadrantes I y$\Pi$. Esto significa que además de una solución de$30^{\circ},$ hay otra solución en Quadrant$\Pi$. Como se mencionó anteriormente, esta solución de segundo cuadrante tiene un ángulo de referencia de$30^{\circ}$

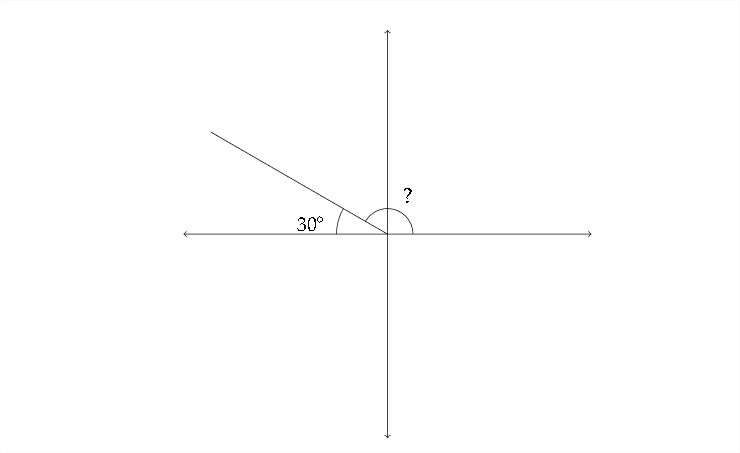
$clipboard_ef50d54f57c94cddc38246beaab70b2ff.png$

Para encontrar este ángulo, simplemente restamos$180^{\circ}-30^{\circ}=150^{\circ}$
En cuadrante$\Pi,$ restamos el ángulo de referencia de$180^{\circ}$
En cuadrante$\Pi$, sumamos el ángulo de referencia a$180^{\circ}$

En Quadrant$\Pi V$, restamos el ángulo de referencia de$360^{\circ}$
So, las soluciones a la ecuación$\sin x=0.5$ entre$0^{\circ}$ y$360^{\circ}$ son$x=30^{\circ}, 150^{\circ}$ En este capítulo consideraremos principalmente soluciones con esta restricción:
\ [ 0^ {\ circ}\ leq x<360^ {\ circ}
\] Las infinitas soluciones a esta ecuación se pueden expresar como:
\ [ 30^ {\ circ} +n\ cdot 360^ {\ circ}\ text {y} 150^ {\ circ} +n\ cdot 360^ {\ circ}
\]

Veamos otro ejemplo:
Ejemplo 2
Encuentra todas las soluciones de la ecuación dada para$0^{\circ} \leq x<360^{\circ}$
$\tan x=4$
Usar una calculadora para encontrar$\tan ^{-1}(4),$ encontramos que devuelve una respuesta de$x \approx 75.96^{\circ}$ Así que esta es la solución a la ecuación que se encuentra en Cuadranti. La función tangente también es positiva en Quadrant$\Pi$, por lo que también debemos considerar el ángulo del tercer cuadrante con un ángulo de referencia de$75.96^{\circ}$

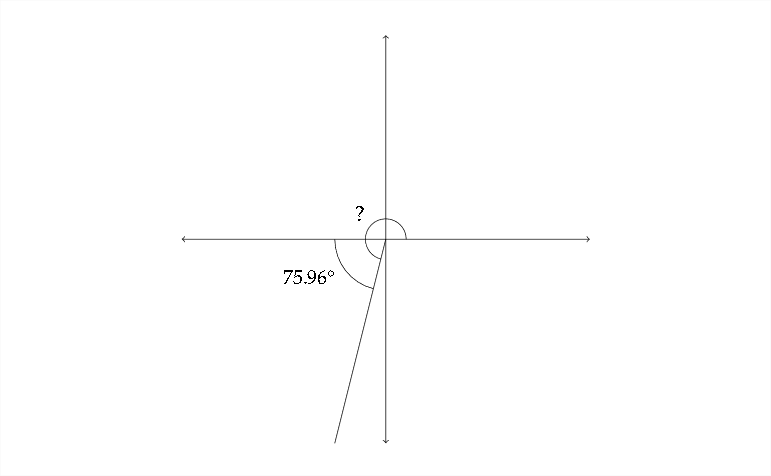
$clipboard_e81a2501214d7b2fda9d5e3ce626c9bd0.png$

En Quadrant$\Pi$, agregamos el ángulo de referencia para$180^{\circ}$
$180^{\circ}+75.96^{\circ}=255.96^{\circ},$ que nuestras soluciones para esta ecuación sean$x \approx 75.96^{\circ}, 255.96^{\circ}$
A menudo, las calculadoras están programadas para devolver un valor de ángulo que no está entre$0^{\circ} \leq x<360^{\circ}$

Ejemplo 3
Encontrar todas las soluciones de la ecuación dada para$0^{\circ} \leq x<360^{\circ}$
$\sin x=-0.25$
Resolver esto en una calculadora TI generalmente devolvería un valor de$-14.5^{\circ} .$ Sin embargo, claramente no$-14.5^{\circ}$ está entre$0^{\circ}$ y$360^{\circ}$, así que necesitamos usar esta información para encontrar las soluciones que se encuentran entre$0^{\circ}$ y$360^{\circ}$

Con la calculadora devolviendo un vlue de$-14.5^{\circ},$ sabemos que el ángulo de referencia para todas las respuestas será$14.5^{\circ} .$ Sabiendo esto, podemos decir que el seno es negativo en los Cuadrantes III y IV, por lo que necesitaremos ángulos en esos cuadrantes con ángulos de referencia de$14.5^{\circ}$

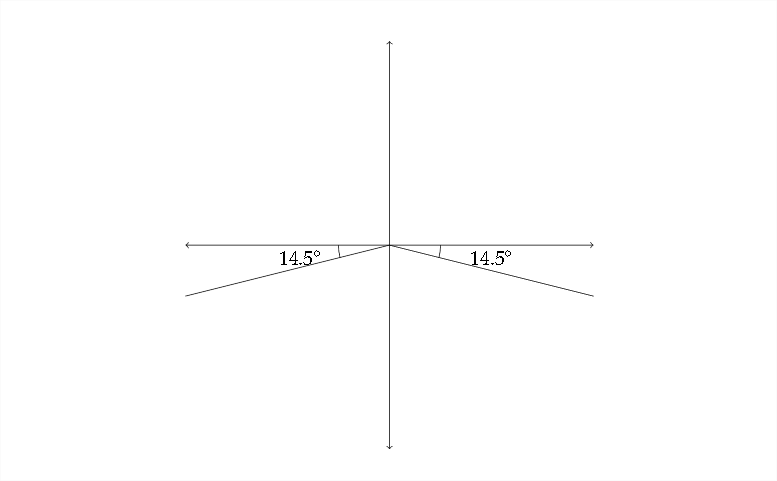
$clipboard_e9bdd93538f5c3ce605983cdb82d26608.png$

En Quadrant$\Pi$ agregaremos$180^{\circ}$ al ángulo de referencia:$180^{\circ}+14.5^{\circ}=194.5^{\circ}$
En Quadrant$\Pi$ restaremos el ángulo de referencia de$360^{\circ}: 360^{\circ}-14.5^{\circ}=345.5^{\circ}$
So,$x \approx 194.5^{\circ}, 345.5^{\circ}$

Algunas ecuaciones trigonométricas no tienen soluciones de números reales. La ecuación no$\sin x=2$ tiene soluciones de números reales. Recordemos que la relación sinusoidal se definió originalmente como la relación del lado opuesto a un ángulo a la hipotenusa. La hipotenusa es siempre el lado más largo de un triángulo rectángulo por lo que no hay forma de que la función sinusoidal pueda ser mayor que 1 si estamos trabajando con ángulos de valor real. Sin embargo, de la misma manera que se utilizan números complejos para resolver ecuaciones como ángulos de$x^{2}=-7,$ valor complejo se pueden usar para resolver ecuaciones como No$\sin x=2$ entraremos en esto aquí, sin embargo, hay una manera relativamente sencilla de resolver estas ecuaciones.
Si encuentras una ecuación como$\cos x=3$ y estás resolviendo valores de$x$$0^{\circ} \leq x<360^{\circ},$ entonces la respuesta adecuada es “ninguna solución” o “ninguna solución real”. Sin embargo, recuerde que la función tangente puede tomar cualquier valor entre$-\infty$ y$\infty$

Ejemplo 4
Resolver una ecuación que incluye una función trigonométrica recíproca simplemente implica el paso extra de encontrar el recíproco:
Encontrar todas las soluciones de la ecuación dada para$0^{\circ} \leq x<360^{\circ}$
$\sec x=12$
El truco aquí es reafirmar la ecuación así que podemos usar los valores preprogramados de una calculadora para encontrar la solución.
Si$\sec x=12$ entonces$\cos x=\frac{1}{12} .$ Finding$\cos ^{-1}\left(\frac{1}{12}\right)$ da una solución de$x \approx 85.2^{\circ}$
El coseno y la secante son ambos positivos en Quadrant$\Pi \mathrm{V}$, así que también querremos un cuarto ángulo de cuadrante cuyo ángulo de referencia sea$85.2^{\circ}$

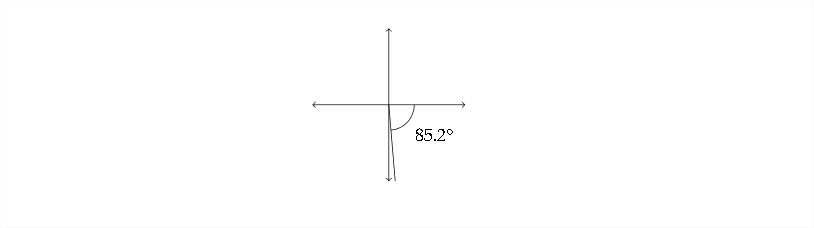
$clipboard_e3961fc6841ea8aae1afed324456b5002.png$

En Quadrant$\Pi$, restaremos el ángulo de referencia de$360^{\circ}$
\ [ \ begin {array} {c}
360^ {\ circ} -85.2^ {\ circ}\ approx 274.8^ {\ circ}\\
x\ approx 85.2^ {\ circ}, 274.8^ {\ circ}
\ end {array}
\]

Ejemplo 5
Resolver una ecuación trigonométrica cuadrática a menudo implica el uso de la fórmula cuadrática:
Encontrar todas las soluciones de la ecuación dada para$0^{\circ} \leq x<360^{\circ}$
$2 \sin ^{2} x-\sin x-2=0$
Usando la fórmula cuadrática llegamos a valores aproximados para$\sin x$ de $\sin x \approx-0.7808,1.2808$
La solución no$\sin x \approx 1.2808$ produce soluciones reales, por lo que nos enfocaremos en resolver$\sin x \approx-0.7808$
Encontrar nos$\sin ^{-1}(-0.7808)$ da una respuesta de$\approx-51.3^{\circ} .$ Esto significa que nuestras respuestas estarán en los Cuadrantes III y IV con ángulos de referencia de$51.3^{\circ} .$ En el Cuadrante III diremos $180^{\circ}+51.3^{\circ} \approx 231.3^{\circ} .$En Quadrant$\mathrm{IV}$, restaremos el ángulo de referencia de$360^{\circ}: 360^{\circ}-51.3^{\circ} \approx 308.7^{\circ}$
$\mathrm{So}, x \approx 231.3^{\circ}, 308.7^{\circ}$

Ejercicios 3.3
Encuentra todas las soluciones para$0^{\circ} \leq x<360^{\circ}$ Redondear todas las medidas$10^{\text {th }}$ de ángulo al grado más cercano.
1. $\cos x-0.75=0$
2. $\sin x+0.432=0$
3. $ 3 \sin x-5=0$
4. $\sin x-4=0$
5. $ 3 \sec x+8=0$
6. $ 4 \csc x+9=0$
7. $ 3-5 \sin x=4 \sin x+1$
8. $ 4 \cos x-5=\cos x-3$
9. $ 3 \tan ^{2} x+2 \tan x=0$
10. $ 4 \cos ^{2} x-\cos x=0$
11. $ 3 \cos ^{2} x+5 \cos x-2=0$
12. $ 2 \cot ^{2} x-7 \cot x+3=0$
13. $ 2 \tan ^{2} x-\tan x-10=0$
14. $ 2 \sin ^{2} x+5 \sin x+3=0$
15. $ 2 \cos ^{2} x-5 \cos x-5=0$
16. $ 3 \sin ^{2} x-\sin x-1=0$