10.4: Más ecuaciones trigonométricas
- Page ID
- 112033
Cuando la solución a una ecuación trigonométrica es uno de los ángulos cuadránticos\(\left(0^{\circ}, 90^{\circ}, 180^{\circ}, 270^{\circ} \text { and } \mathrm{so} \text { on }\right),\) entonces determinar todas las soluciones entre\(0^{\circ}\) y\(360^{\circ}\) puede funcionar un poco diferente. La calculadora devolverá algunos de estos valores, pero en algunos casos puede que no. Si volvemos al círculo unitario, podemos ver esto más claramente:
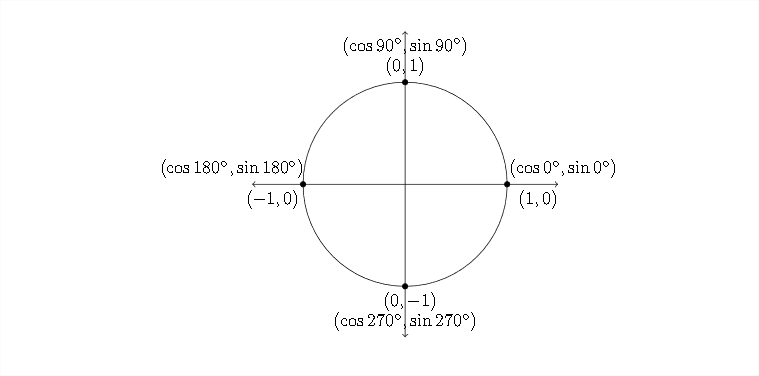
En el diagrama anterior podemos ver el seno y el coseno para\(0^{\circ}, 90^{\circ}, 180^{\circ},\) y\(270^{\circ}\) desde\(\tan \theta=\frac{\sin \theta}{\cos \theta},\) entonces podemos ver que\(\tan 0^{\circ}=0, \tan 90^{\circ}\) está indefinido,\(\tan 180^{\circ}=\)
0 y también\(\tan 270^{\circ}\) es indefinido.
El problema real con los ángulos cuadránticos es encontrar\(\sin ^{-1}(0), \cos ^{-1}(0)\) o\(\tan ^{-1}(0)\) La calculadora devuelve valores de:
\ [
\ begin {array} {l}
\ sin ^ {-1} (0) =0^ {\ circ}\\
\ cos ^ {-1} (0) =90^ {\ circ}\\
\ tan ^ {-1} (0) =0^ {\ circ}
\ end {array}
\]
En cada caso, existe otra posibilidad que difiere del ángulo dado por\(180^{\circ}\) así:
\ [
\ begin {array} {l}
\ sin ^ {-1} (0) =0^ {\ circ}, 180^ {\ circ}\
\ circ}\\ cos ^ {-1} (0) =90^ {\ circ}, 270^ {\ circ}
\\\ tan ^ {-1} (0) =0^ {\ circ}, 180^ {
\ circ}
\ end {array}\]
Veamos cómo se usa esto para resolver una ecuación:
Ejemplo 1
Resolver la ecuación dada para\(0^{\circ} \leq x<360^{\circ}\)
\ [\ tan ^ {2} x-\ tan x=0
\]
Podríamos usar la fórmula cuadrática para resolver esto, pero también podemos resolver factorizando:
\ [
\ begin {array} {c}
\ tan ^ {2} x-\ tan x=0\\
\ tan x (\ tan x-1) =0\\
\ tan x=0\ text {or}\ tan x=1
\ end {array}
\]
Usando una calculadora para encontrar\(\tan ^{-1}(0)\) y\(\tan ^{-1}(1)\) devuelve valores de\(\tan ^{-1}(0)=0^{\circ}\) y\(\tan ^{-1}(1)=45^{\circ} .\) Una vez que conocemos el ángulo de referencia para\(\tan ^{-1}(1),\) entonces sabemos que ya que la tangente es también positivo en Quadrant\(\Pi I\), las soluciones aquí son\(45^{\circ}\) y\(225^{\circ} .\) La calculadora devuelve una respuesta de\(0^{\circ}\) for\(\tan ^{-1}(0),\) pero acabamos de ver eso\(\tan 180^{\circ}=0\) también.
Las respuestas para esta ecuación son\(x=45^{\circ}, 225^{\circ}, 0^{\circ}, 180^{\circ}\)
Otro enfoque para resolver ecuaciones trigonométricas implica el uso de Identidades Pitágoras para hacer una sustitución que de manera que la ecuación pueda resolverse simplemente por la fórmula cuadrática. Aquí hay un ejemplo:
Ejemplo 2
Resuelve la ecuación dada para\(0^{\circ} \leq x<360^{\circ}\)
\ [
\ sin ^ {2}\ theta-6\ cos\ theta=4
\]
Observe que, a diferencia de los problemas que vimos en la sección anterior, esta ecuación involucra tanto el seno como el coseno. Para remediar esto, podemos sustituir el\(\sin ^{2} \theta\) término con la expresión\(1-\cos ^{2} \theta\)
\ [
\ begin {array} {c}
\ sin ^ {2}\ theta-6\ cos\ theta=4\\
1-\ cos ^ {2}\ theta-6\ cos\ theta=4\\
0=\ cos ^ {2}\ theta+6\ cos\ theta+3
\ end {array}
\]
usando la fórmula cuadrática:
\ [
\ cos\ theta\ approx-5.449, -0.5505
\]
ya que no\(\cos ^{-1}(-5.449)\) es un ángulo de valor real, podemos enfocarnos en la otra respuesta:
\(\cos ^{-1}(-0.5505) \approx 123.4^{\circ} .\) dado que la función coseno también es negativa en el tercer cuadrante, necesitamos encontrar el ángulo de referencia que nos ayude a identificar el ángulo del tercer cuadrante que es una solución para esta ecuación:
\ [
180^ {\ circ} -123.4^ {\ circ} =56.6^ {\ circ}
\]
Así que el ángulo de referencia es\(56.6^{\circ}\)
\ [
180^ {\ circ} +56.6^ {\ circ} =236.6^ {\ circ}
\]
Las soluciones son\(\theta \approx 123.4^{\circ}, 236.6^{\circ}\)
Ejemplo 3
Resolver la ecuación dada para\(0^{\circ} \leq x<360^{\circ}\)
\ [
2\ cos ^ {2}\ theta-\ sin\ theta=\ sin ^ {2}\ theta+1
\]
Primero, sustituiremos\(1-\sin ^{2} \theta\) por el\(\cos ^{2} \theta\)
\ [
\ begin {array} {c}
2\ cos ^ {2}\ theta-\ sin\ theta=\ sin ^ {2}\ theta+1\\
2\ left (1-\ sin ^ {2}\ theta\ right) -\ sin\ theta=\ sin ^ {2}\ theta+1\
2-2\ sin ^ {2}\ theta-\ sin\ theta=\ sin ^ {2}\ theta+1\\
0=3\ sin ^ {2}\ theta+\ sin\ theta-1
\ end {array}
\]
Resolver esto con la fórmula cuadrática nos da soluciones de\(\sin \theta \approx-0.7676,0.43426\)
\ [\ sin ^ {-1} (-0.7676)\ approx-50.1^ {\ circ}
\]
\ [
\ sin ^ {-1} (0.43426)\ approx 25.7^ {\ circ}
\]
Primero trabajaremos con la solución positiva. ya que el seno también es positivo en el Cuadrante II, el otro ángulo será\(180^{\circ}-25.7^{\circ}=154.3^{\circ}\)
Para la solución negativa, sabemos que el seno es negativo en los Cuadrantes III y\(\mathrm{IV},\) así con un ángulo de referencia de\(50.1^{\circ},\) en el tercer cuadrante\(180^{\circ}+50.1^{\circ}=230.1^{\circ}\) y en el cuarto cuadrante\(360^{\circ}-50.1^{\circ}=309.9^{\circ}\)
El conjunto de soluciones es\(\theta \approx 25.7^{\circ}, 154.3^{\circ}, 230.1^{\circ}, 309.9^{\circ}\)
Ejercicios 3.4
Resolver las ecuaciones dadas para\(0^{\circ} \leq x<360^{\circ}\)
1. \(\quad 9 \sin ^{2} \theta-6 \sin \theta=1\)
2. \(\quad 4 \cos ^{2} \theta+4 \cos \theta=1\)
3. \(\quad \sec ^{2} \alpha-2 \sec \alpha-3=0\)
4. \(\quad \csc ^{2} \beta+4 \csc \beta-10=0\)
5. \(\quad \csc ^{2} x+4 \csc x-7=0\)
6. \(\quad 3 \cot ^{2} x-3 \cot x-1=0\)
7. \(\quad 2 \sin ^{2} x=1-\cos x\)
8. \(\quad \cos ^{2} \alpha+4=2 \sin \alpha-3\)
9. \(\quad \cos ^{2} \beta-3 \sin \beta+2 \sin ^{2} \beta=0\)
10. \(\quad \sin ^{2} \theta=2 \cos \theta+3 \cos ^{2} \theta\)
11. \(\quad \sec ^{2} x=2 \tan x+4\)
12. \(\quad 3 \tan ^{2} x=\sec x+2\)
13. \(\quad \cos \alpha+1=2 \cos 2 \alpha\)
14. \(\quad \cos 2 x-3 \sin x-2=0\)
15. \(\quad \csc ^{2} \theta=\cot \theta+5\)
16. \(\quad \csc \theta+5=2 \cot ^{2} \theta+2\)


