8.3: Funciones trigonométricas inversas

Objetivos de aprendizaje

• Comprender y usar las funciones sinusoidales inversas, coseno y tangente.
• Encuentra el valor exacto de las expresiones que involucran las funciones de seno inverso, coseno y tangente.
• Utilice una calculadora para evaluar funciones trigonométricas inversas.
• Encuentra valores exactos de funciones compuestas con funciones trigonométricas inversas.

Para cualquier triángulo rectángulo, dado otro ángulo y la longitud de un lado, podemos averiguar cuáles son los otros ángulos y lados. Pero, ¿y si nos dan solo dos lados de un triángulo rectángulo? Necesitamos un procedimiento que nos lleve de una relación de lados a un ángulo. Aquí es donde entra en juego la noción de una función inversa a una función trigonométrica. En esta sección, exploraremos las funciones trigonométricas inversas.

Comprensión y uso de las funciones de seno inverso, coseno y tangente

Para utilizar funciones trigonométricas inversas, necesitamos entender que una función trigonométrica inversa “deshace” lo que “hace” la función trigonométrica original, como es el caso de cualquier otra función y su inversa. En otras palabras, el dominio de la función inversa es el rango de la función original, y viceversa, como se resume en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\)

Por ejemplo, si\(f(x)=\sin\space x\), entonces escribiríamos\(f^{−1}(x)={\sin}^{−1}x\). Ten en cuenta que eso\({\sin}^{−1}x\) no significa\(\dfrac{1}{\sin\space x}\). Los siguientes ejemplos ilustran las funciones trigonométricas inversas:

• Desde\(\sin\left(\dfrac{\pi}{6}\right)=\dfrac{1}{2}\) entonces\(\dfrac{\pi}{6}={\sin}^{−1}\left(\dfrac{1}{2}\right)\).
• Desde\(\cos(\pi)=−1\) entonces\(\pi={\cos}^{−1}(−1)\).
• Desde\(\tan\left (\dfrac{\pi}{4}\right )=1\) entonces\(\dfrac{\pi}{4}={\tan}^{−1}(1)\).

En secciones anteriores, evaluamos las funciones trigonométricas en varios ángulos, pero a veces necesitamos saber qué ángulo produciría un valor específico de seno, coseno o tangente. Para ello, necesitamos funciones inversas. Recordemos que, para una función uno a uno, si\(f(a)=b\), entonces una función inversa satisfacería\(f^{−1}(b)=a\).

Tenga en cuenta que las funciones seno, coseno y tangente no son funciones uno a uno. La gráfica de cada función fallaría en la prueba de línea horizontal. De hecho, ninguna función periódica puede ser uno a uno porque cada salida en su rango corresponde a al menos una entrada en cada período, y hay un número infinito de períodos. Al igual que con otras funciones que no son uno a uno, necesitaremos restringir el dominio de cada función para producir una nueva función que sea uno a uno. Elegimos un dominio para cada función que incluya el número 0. La figura\(\PageIndex{2}\) muestra la gráfica de la función sinusoidal limitada a\(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\) y la gráfica de la función coseno limitada a\([ 0,\pi ]\).

Figura\(\PageIndex{2}\): (a) Función sinusoidal en un dominio restringido de\(\left[ −\dfrac{\pi}{2}, \dfrac{\pi}{2} \right]\); (b) Función coseno en un dominio restringido de\([ 0,\pi ]\)

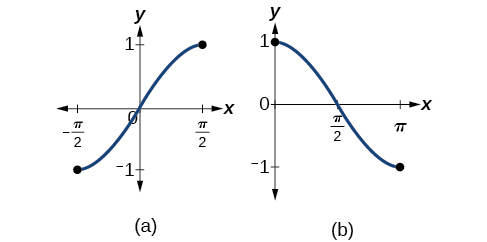
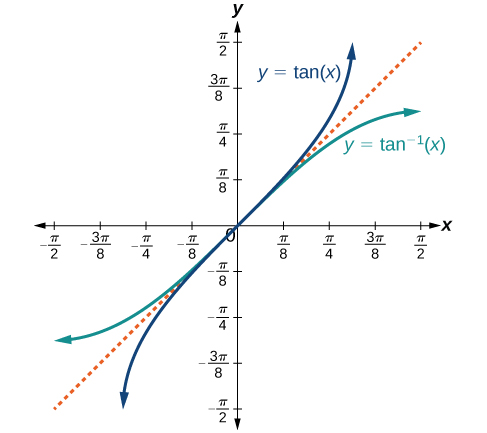
La figura\(\PageIndex{3}\) muestra la gráfica de la función tangente limitada a\(\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right)\).

Figura\(\PageIndex{3}\): Función tangente en un dominio restringido de\(\left (−\dfrac{\pi}{2},\dfrac{\pi}{2}\right )\)

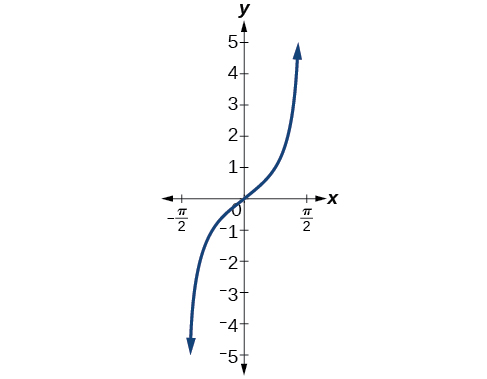
Estas elecciones convencionales para el dominio restringido son algo arbitrarias, pero tienen características importantes y útiles. Cada dominio incluye el origen y algunos valores positivos, y lo más importante, cada uno da como resultado una función uno a uno que es invertible. La elección convencional para el dominio restringido de la función tangente también tiene la propiedad útil de que se extiende de una asíntota vertical a la siguiente en lugar de estar dividida en dos partes por una asíntota.

En estos dominios restringidos, podemos definir las funciones trigonométricas inversas.

• La función sinusoidal inversa\(y={\sin}^{−1}x\) significa\(x=\sin\space y\). La función sinusoidal inversa a veces se llama la función arcoseno, y se nota\(\arcsin\space x\).

  \(y={\sin}^{−1}x\)tiene dominio\([−1,1]\) y rango\(\left[−\frac{\pi}{2},\frac{\pi}{2}\right]\)

• La función coseno inversa\(y={\cos}^{−1}x\) significa\(x=\cos\space y\). La función coseno inversa a veces se llama la función arcoseno, y se nota\(\arccos\space x\).

  \(y={\cos}^{−1}x\)tiene dominio\([−1,1]\) y rango\([0,π]\)

• La función tangente inversa\(y={\tan}^{−1}x\) significa\(x=\tan\space y\). La función tangente inversa a veces se llama la función arcotangente, y se nota\(\arctan\space x\).

  \(y={\tan}^{−1}x\)tiene dominio\((−\infty,\infty)\) y rango\(\left(−\frac{\pi}{2},\frac{\pi}{2}\right)\)

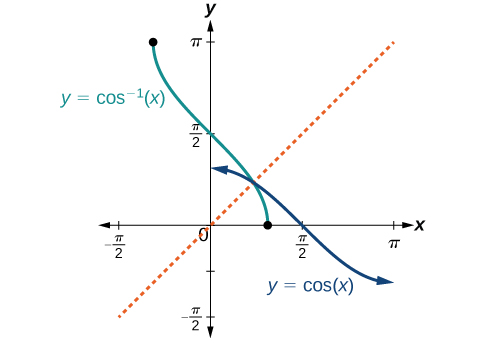
Las gráficas de las funciones inversas se muestran en las Figuras\(\PageIndex{4}\) -\(\PageIndex{6}\). Observe que la salida de cada una de estas funciones inversas es un número, un ángulo en medida de radianes. Vemos que\({\sin}^{−1}x\) tiene dominio\([ −1,1 ]\) y rango\(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\),\({\cos}^{−1}x\) tiene dominio\([ −1,1 ]\) y rango\([0,\pi]\), y\({\tan}^{−1}x\) tiene dominio de todos los números reales y rango\(\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right)\). Para encontrar el dominio y rango de funciones trigonométricas inversas, cambie el dominio y rango de las funciones originales. Cada gráfica de la función trigonométrica inversa es un reflejo de la gráfica de la función original sobre la línea\(y=x\).

Figura\(\PageIndex{4}\): La función sinusoidal y la función sinusoidal inversa (o arcoseno)

Figura\(\PageIndex{5}\): La función coseno y la función coseno inversa (o arcoseno)

Figura\(\PageIndex{6}\): La función tangente y la función tangente inversa (o arcotangente)

RELACIONES PARA FUNCIONES INVERSINO, COSINO Y TANGENTE

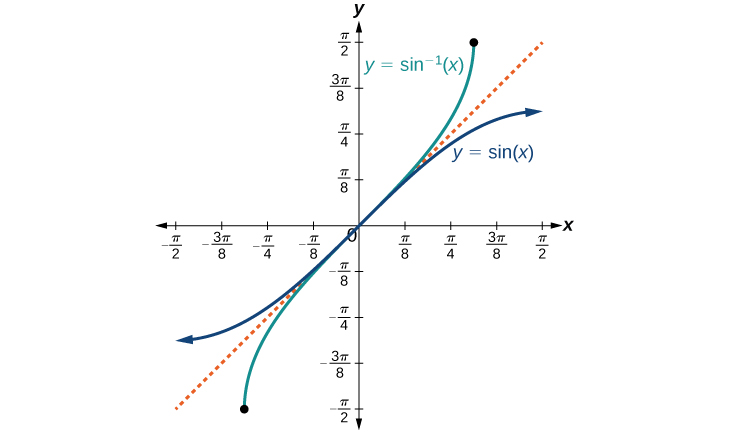
Para ángulos en el intervalo\(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\), si\(\sin y=x\), entonces\({\sin}^{−1}x=y\).

Para ángulos en el intervalo\([ 0,\pi ]\), si\(\cos y=x\), entonces\({\cos}^{−1}x=y\).

Para ángulos en el intervalo\(\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right )\), si\(\tan y=x\), entonces\({\tan}^{−1}x=y\).

Ejemplo\(\PageIndex{1}\): Writing a Relation for an Inverse Function

Dado\(\sin\left(\dfrac{5\pi}{12}\right)≈0.96593\), escribir una relación que involucre el seno inverso.

Solución

Usa la relación para el seno inverso. Si\(\sin y=x\), entonces\({\sin}^{−1}x=y\).

En este problema,\(x=0.96593\), y\(y=\dfrac{5\pi}{12}\).

\({\sin}^{−1}(0.96593)≈\dfrac{5\pi}{12}\)

Ejercicio\(\PageIndex{1}\)

Dado\(\cos(0.5)≈0.8776\), escribir una relación que involucre el coseno inverso.

Contestar

\(\arccos(0.8776)≈0.5\)

Encontrar el valor exacto de las expresiones que involucran las funciones de seno inverso, coseno y tangente

Ahora que podemos identificar funciones inversas, aprenderemos a evaluarlas. Para la mayoría de los valores en sus dominios, debemos evaluar las funciones trigonométricas inversas usando una calculadora, interpolando de una tabla o usando alguna otra técnica numérica. Al igual que hicimos con las funciones trigonométricas originales, podemos dar valores exactos para las funciones inversas cuando estamos usando los ángulos especiales, específicamente\(\dfrac{\pi}{6}\) (30°),\(\dfrac{\pi}{4}\) (45°) y\(\dfrac{\pi}{3}\) (60°), y sus reflexiones en otros cuadrantes.

Dado un valor de entrada “especial”, evaluar una función trigonométrica inversa.

1. Encontrar ángulo\(x\) para el cual la función trigonométrica original tiene una salida igual a la entrada dada para la función trigonométrica inversa.
2. Si no\(x\) está en el rango definido de la inversa, busque otro ángulo\(y\) que esté en el rango definido y tenga el mismo seno, coseno o tangente que\(x\), dependiendo de cuál corresponda a la función inversa dada.

Ejemplo\(\PageIndex{2}\): Evaluating Inverse Trigonometric Functions for Special Input Values

Evaluar cada uno de los siguientes.

1. \({\sin}^{−1}\left(\dfrac{1}{2}\right)\)
2. \({\sin}^{−1}\left(−\dfrac{\sqrt{2}}{2}\right)\)
3. \({\cos}^{−1}\left(−\dfrac{\sqrt{3}}{2}\right)\)
4. \({\tan}^{−1}(1)\)

Solución

1. Evaluar\({\sin}^{−1}\left(\dfrac{1}{2}\right)\) es lo mismo que determinar el ángulo que tendría un valor sinusoidal de\(\dfrac{1}{2}\). En otras palabras, ¿qué ángulo\(x\) satisfaría\(\sin(x)=\dfrac{1}{2}\)? Hay múltiples valores que satisfacerían esta relación, como\(\dfrac{\pi}{6}\) y\(\dfrac{5\pi}{6}\), pero sabemos que necesitamos el ángulo en el intervalo\(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\), entonces la respuesta será\({\sin}^{−1}\left (\dfrac{1}{2}\right)=\dfrac{\pi}{6}\). Recuerda que la inversa es una función, así que para cada entrada, obtendremos exactamente una salida.
2. Para evaluar\({\sin}^{−1}\left(−\dfrac{\sqrt{2}}{2}\right)\), sabemos que\(\dfrac{5\pi}{4}\) y\(\dfrac{7\pi}{4}\) ambos tienen un valor sinusoidal de\(-\dfrac{\sqrt{2}}{2}\), pero ninguno está en el intervalo\(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\). Para ello, necesitamos el coterminal de ángulo negativo con\(\dfrac{7\pi}{4}\):\({\sin}^{−1}\left(−\dfrac{\sqrt{2}}{2}\right)=−\dfrac{\pi}{4}\).
3. Para evaluar\({\cos}^{−1}\left(−\dfrac{\sqrt{3}}{2}\right)\), estamos buscando un ángulo en el intervalo\([ 0,\pi ]\) con un valor coseno de\(-\dfrac{\sqrt{3}}{2}\). El ángulo que satisface esto es\({\cos}^{−1}\left(−\dfrac{\sqrt{3}}{2}\right)=\dfrac{5\pi}{6}\).
4. Evaluando\({\tan}^{−1}(1)\), estamos buscando un ángulo en el intervalo\(\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right)\) con un valor tangente de\(1\). El ángulo correcto es\({\tan}^{−1}(1)=\dfrac{\pi}{4}\).

Ejercicio\(\PageIndex{2}\)

Evaluar cada uno de los siguientes.

1. \({\sin}^{−1}(−1)\)
2. \({\tan}^{−1}(−1)\)
3. \({\cos}^{−1}(−1)\)
4. \({\cos}^{−1}\left(\dfrac{1}{2}\right)\)

Contestar a

\(-\dfrac{\pi}{2}\)

Respuesta b

\(-\dfrac{\pi}{4}\)

Respuesta c

\(\pi\)

Respuesta d

\(\dfrac{\pi}{3}\)

Uso de una calculadora para evaluar funciones trigonométricas inversas

Para evaluar funciones trigonométricas inversas que no involucren los ángulos especiales discutidos anteriormente, necesitaremos usar una calculadora u otro tipo de tecnología. La mayoría de las calculadoras científicas y las aplicaciones emuladoras de calculadoras tienen teclas o botones específicos para las funciones sinusoidales inversas, coseno y tangente. Estos pueden estar etiquetados, por ejemplo, SIN-1, ARCSIN o ASIN.

En el capítulo anterior, se trabajó con trigonometría en un triángulo rectángulo para resolver los lados de un triángulo dado un lado y un ángulo adicional. Usando las funciones trigonométricas inversas, podemos resolver los ángulos de un triángulo rectángulo dados dos lados, y podemos usar una calculadora para encontrar los valores a varios decimales.

En estos ejemplos y ejercicios, las respuestas se interpretarán como ángulos y las usaremos\(\theta\) como la variable independiente. El valor que se muestra en la calculadora puede estar en grados o radianes, así que asegúrese de establecer el modo apropiado para la aplicación.

Ejemplo\(\PageIndex{3}\): Evaluating the Inverse Sine on a Calculator

Evaluar\({\sin}^{−1}(0.97)\) usando una calculadora.

Solución

Debido a que la salida de la función inversa es un ángulo, la calculadora nos dará un valor de grado si está en modo grado y un valor de radianes si está en modo radián. Las calculadoras también usan las mismas restricciones de dominio en los ángulos que estamos usando.

En modo radián,\({\sin}^{−1}(0.97)≈1.3252\). En modo grado,\({\sin}^{−1}(0.97)≈75.93°\). Tenga en cuenta que en cálculo y más allá usaremos radianes en casi todos los casos.

Ejercicio\(\PageIndex{3}\)

Evaluar\({\cos}^{−1}(−0.4)\) usando una calculadora.

Contestar

\(1.9823\)o\(113.578^{\circ}\)

Dados dos lados de un triángulo rectángulo como el que se muestra en la Figura 8.4.7, encontrar un ángulo.

Figura\(\PageIndex{7}\)

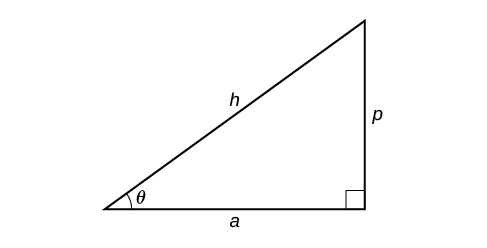
1. Si un lado dado es la hipotenusa de longitud\(h\) y se da el lado de longitud\(a\) adyacente al ángulo deseado, use la ecuación\(\theta={\cos}^{−1}\left(\dfrac{a}{h}\right)\).
2. Si un lado dado es la hipotenusa de longitud\(h\) y se da el lado de longitud\(p\) opuesto al ángulo deseado, use la ecuación\(\theta={\sin}^{−1}\left(\dfrac{p}{h}\right)\).
3. Si se dan las dos patas (los lados adyacentes al ángulo recto), entonces use la ecuación\(\theta={\tan}^{−1}\left(\dfrac{p}{a}\right)\).

Ejemplo\(\PageIndex{4}\): Applying the Inverse Cosine to a Right Triangle

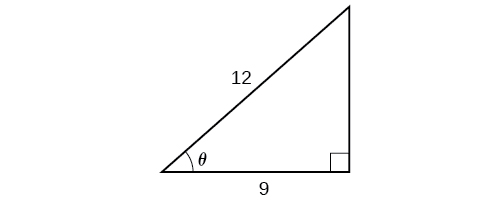
Resuelve el triángulo en la Figura\(\PageIndex{8}\) para el ángulo\(\theta\).

Figura\(\PageIndex{8}\)

Solución

Debido a que conocemos la hipotenusa y el lado adyacente al ángulo, tiene sentido que usemos la función coseno.

\[\begin{align*} \cos \theta&= \dfrac{9}{12}\\ \theta&= {\cos}^{-1}\left(\dfrac{9}{12}\right)\qquad \text{Apply definition of the inverse}\\ \theta&\approx 0.7227\qquad \text{or about } 41.4096^{\circ} \text{ Evaluate} \end{align*}\]

Ejercicio\(\PageIndex{4}\)

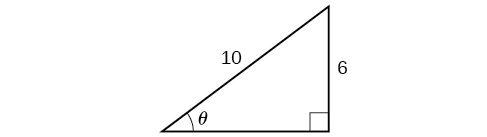
Resuelve el triángulo en la Figura\(\PageIndex{9}\) para el ángulo\(\theta\).

Figura\(\PageIndex{9}\)

Contestar

\({\sin}^{−1}(0.6)=36.87°=0.6435\)radianes

Búsqueda de valores exactos de funciones compuestas con funciones trigonométricas inversas

Hay momentos en los que necesitamos componer una función trigonométrica con una función trigonométrica inversa. En estos casos, normalmente podemos encontrar valores exactos para las expresiones resultantes sin recurrir a una calculadora. Incluso cuando la entrada a la función compuesta es una variable o una expresión, a menudo podemos encontrar una expresión para la salida. Para ayudar a ordenar diferentes casos, dejar\(f(x)\) y\(g(x)\) ser dos funciones trigonométricas diferentes pertenecientes al conjunto {\(\sin(x)\),\(\cos(x)\),\(\tan(x)\)} y dejar\(f^{-1}(y)\) y\(g^{-1}(y)\) ser sus inversas.

Evaluación de Composiciones de la Forma\(f(f^{-1}(y))\) y\(f^{-1}(f(x))\)

Para cualquier función trigonométrica,\(f(f^{-1}(y))=y\) para todos\(y\) en el dominio adecuado para la función dada. Esto se desprende de la definición de lo inverso y del hecho de que el rango de se\(f\) definió como idéntico al dominio de\(f^{−1}\). No obstante, hay que ser un poco más cuidadosos con las expresiones de la forma\(f^{-1}(f(x))\).

Composiciones de una función trigonométrica y su inversa

\[\begin{align*} \sin({\sin}^{-1}x)&= x\qquad \text{for } -1\leq x\leq 1\\ \cos({\cos}^{-1}x)&= x\qquad \text{for } -1\leq x\leq 1\\ \tan({\tan}^{-1}x)&= x\qquad \text{for } -\infty<x<\infty\\ {\sin}^{-1}(\sin x)&= x\qquad \text{only for } -\dfrac{\pi}{2}\leq x\leq \dfrac{\pi}{2}\\ {\cos}^{-1}(\cos x)&= x\qquad \text{only for } 0\leq x\leq \pi\\ {\tan}^{-1}(\tan x)& =x\qquad \text{only for } -\dfrac{\pi}{2}< x< \dfrac{\pi}{2} \end{align*}\]

Q&A

¿Es correcto eso\({\sin}^{−1}(\sin x)=x\)?

No. Esta ecuación es correcta ifx x pertenece al dominio restringido\(\left[−\dfrac{\pi}{2},\dfrac{\pi}{2}\right]\), pero seno se define para todos los valores de entrada reales, y para\(x\) fuera del intervalo restringido, la ecuación no es correcta porque su inversa siempre devuelve un valor in\(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\). La situación es similar para coseno y tangente y sus inversos. Por ejemplo,\({\sin}^{−1}\left(\sin\left(\dfrac{3\pi}{4}\right)\right)=\dfrac{\pi}{4}\).

Dada una expresión de la forma\(f^{-1}(f(\theta))\) where \(f(\theta)=\sin \theta\), \(\cos \theta\), or \(\tan \theta\), evaluate.

1. Si\(\theta\) está en el dominio restringido de\(f\), entonces\(f^{−1}(f(\theta))=\theta\).
2. Si no, entonces encuentra un ángulo\(\phi\) dentro del dominio restringido fuera de f tal que\(f(\phi)=f(\theta)\). Entonces\(f^{−1}(f(\theta))=\phi\).

Ejemplo\(\PageIndex{5}\): Using Inverse Trigonometric Functions

Evalúe lo siguiente:

1. \({\sin}^{−1}\left (\sin \left(\dfrac{\pi}{3}\right )\right )\)
2. \({\sin}^{−1}\left (\sin \left(\dfrac{2\pi}{3}\right )\right )\)
3. \({\cos}^{−1}\left (\cos \left (\dfrac{2\pi}{3}\right )\right )\)
4. \({\cos}^{−1}\left (\cos \left (−\dfrac{\pi}{3}\right )\right )\)

Solución

1. \(\dfrac{\pi}{3}\)está en\(\left[−\dfrac{\pi}{2},\dfrac{\pi}{2}\right]\), entonces\({\sin}^{−1}\left(\sin\left(\dfrac{\pi}{3}\right)\right)=\dfrac{\pi}{3}\).
2. \(\dfrac{2\pi}{3}\)no está en\(\left[−\dfrac{\pi}{2},\dfrac{\pi}{2}\right]\), pero\(sin\left(\dfrac{2\pi}{3}\right)=sin\left(\dfrac{\pi}{3}\right)\), entonces\({\sin}^{−1}\left(\sin\left(\dfrac{2\pi}{3}\right)\right)=\dfrac{\pi}{3}\).
3. \(\dfrac{2\pi}{3}\)está en\([ 0,\pi ]\), entonces\({\cos}^{−1}\left(\cos\left(\dfrac{2\pi}{3}\right)\right)=\dfrac{2\pi}{3}\).
4. \(-\dfrac{\pi}{3}\)no está en\([ 0,\pi ]\), sino\(\cos\left(−\dfrac{\pi}{3}\right)=\cos\left(\dfrac{\pi}{3}\right)\) porque el coseno es una función par. \(\dfrac{\pi}{3}\)está en\([ 0,\pi ]\), entonces\({\cos}^{−1}\left(\cos\left(−\dfrac{\pi}{3}\right)\right)=\dfrac{\pi}{3}\).

Ejercicio\(\PageIndex{5}\)

Evaluar\({\tan}^{−1}\left(\tan\left(\dfrac{\pi}{8}\right)\right)\) y\({\tan}^{−1}\left(\tan\left(\dfrac{11\pi}{9}\right)\right)\).

Contestar

\(\dfrac{\pi}{8}\);\(\dfrac{2\pi}{9}\)

Evaluación de Composiciones de la Forma\(f^{-1}(g(x))\)

Ahora que podemos componer una función trigonométrica con su inversa, podemos explorar cómo evaluar una composición de una función trigonométrica y la inversa de otra función trigonométrica. Comenzaremos con composiciones de la forma\(f^{-1}(g(x))\). Para valores especiales de\(x\), podemos evaluar exactamente la función interna y luego la externa, función inversa. Sin embargo, podemos encontrar un enfoque más general al considerar la relación entre los dos ángulos agudos de un triángulo rectángulo donde está uno\(\theta\), haciendo el\(\dfrac{\pi}{2}−\theta\) otro.Considere el seno y el coseno de cada ángulo del triángulo rectángulo en la Figura\(\PageIndex{10}\).

Figura\(\PageIndex{10}\): Triángulo recto que ilustra las relaciones de cofunción

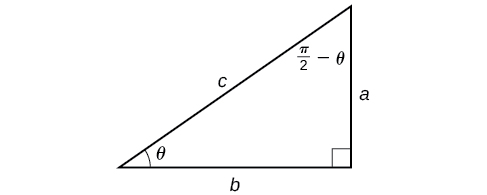
Porque\(\cos \theta=\dfrac{b}{c}=sin\left(\dfrac{\pi}{2}−\theta\right)\), tenemos\({\sin}^{−1}(\cos \theta)=\dfrac{\pi}{2}−\theta\) si\(0≤\theta≤\pi\). Si no\(\theta\) está en este dominio, entonces necesitamos encontrar otro ángulo que tenga el mismo coseno que\(\theta\) y que pertenezca al dominio restringido; entonces restamos este ángulo de\(\dfrac{\pi}{2}\) .Similarmente,\(\sin \theta=\dfrac{a}{c}=\cos\left(\dfrac{\pi}{2}−\theta\right)\), así que\({\cos}^{−1}(\sin \theta)=\dfrac{\pi}{2}−\theta\) si\(−\dfrac{\pi}{2}≤\theta≤\dfrac{\pi}{2}\). Estas son solo las relaciones función-cofunción presentadas de otra manera.

Dadas las funciones de la forma\({\sin}^{−1}(\cos x)\) and \({\cos}^{−1}(\sin x)\), evaluate them.

1. Si\(x\) está en\([ 0,\pi ]\), entonces\({\sin}^{−1}(\cos x)=\dfrac{\pi}{2}−x\).
2. Si no\(x\) está adentro\([ 0,\pi ]\), entonces encuentra otro ángulo\(y\) en\([ 0,\pi ]\) tal que\(\cos y=\cos x\).

   \[{\sin}^{−1}(\cos x)=\dfrac{\pi}{2}−y\]

3. Si\(x\) está en\(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\), entonces\({\cos}^{−1}(\sin x)=\dfrac{\pi}{2}−x\).
4. Si no\(x\) está adentro\(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\), entonces encuentra otro ángulo\(y\) en\(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\) tal que\(\sin y=\sin x\).

   \[{\cos}^{−1}(\sin x)=\dfrac{\pi}{2}−y\]

Ejemplo\(\PageIndex{6}\): Evaluating the Composition of an Inverse Sine with a Cosine

Evaluar\({\sin}^{−1}\left(\cos\left(\dfrac{13\pi}{6}\right)\right)\)

1. por evaluación directa.
2. por el método descrito anteriormente.

Solución

1. Aquí, podemos evaluar directamente el interior de la composición. \[\begin{align*} \cos\left(\dfrac{13\pi}{6}\right)&= \cos\left (\dfrac{\pi}{6}+2\pi\right )\\ &= \cos\left (\dfrac{\pi}{6}\right )\\ &= \dfrac{\sqrt{3}}{2} \end{align*}\]Ahora, podemos evaluar la función inversa como hicimos antes. \[{\sin}^{−1}\left (\dfrac{\sqrt{3}}{2}\right )=\dfrac{\pi}{3}\]
2. Tenemos\(x=\dfrac{13\pi}{6}\),\(y=\dfrac{\pi}{6}\), y\[\begin{align*} {\sin}^{-1}\left (\cos \left (\dfrac{13\pi}{6} \right ) \right )&= \dfrac{\pi}{2}-\dfrac{\pi}{6}\\ &= \dfrac{\pi}{3} \end{align*}\]

Ejercicio\(\PageIndex{6}\)

Evaluar\({\cos}^{−1}\left (\sin\left (−\dfrac{11\pi}{4}\right )\right )\).

Contestar

\(\dfrac{3\pi}{4}\)

Evaluación de Composiciones de la Forma\(f(g^{−1}(x))\)

Para evaluar composiciones de la forma\(f(g^{−1}(x))\), donde\(f\) y\(g\) son cualesquiera dos de las funciones seno, coseno, o tangente y\(x\) es cualquier entrada en el dominio de\(g^{−1}\), tenemos fórmulas exactas, tales como\(\sin({\cos}^{−1}x)=\sqrt{1−x^2}\). Cuando necesitamos usarlos, podemos derivar estas fórmulas usando las relaciones trigonométricas entre los ángulos y lados de un triángulo rectángulo, junto con el uso de la relación de Pitágoras entre las longitudes de los lados. Podemos usar la identidad pitagórica,\({\sin}^2 x+{\cos}^2 x=1\), para resolver para uno cuando se le da el otro. También podemos usar las funciones trigonométricas inversas para encontrar composiciones que involucren expresiones algebraicas.

Ejemplo\(\PageIndex{7}\): Evaluating the Composition of a Sine with an Inverse Cosine

Encuentra un valor exacto para\(\sin\left({\cos}^{−1}\left(\dfrac{4}{5}\right)\right)\).

Solución

Comenzando por el interior, podemos decir que hay algún ángulo tal que\(\theta={\cos}^{−1}\left (\dfrac{4}{5}\right )\), lo que significa\(\cos \theta=\dfrac{4}{5}\), y estamos buscando\(\sin \theta\). Podemos usar la identidad pitagórica para hacer esto.

\[\begin{align*} {\sin}^2 \theta+{\cos}^2 \theta&= 1\qquad \text{Use our known value for cosine}\\ {\sin}^2 \theta+{\left (\dfrac{4}{5} \right )}^2&= 1\qquad \text{Solve for sine}\\ {\sin}^2 \theta&= 1-\dfrac{16}{25}\\ \sin \theta&=\pm \dfrac{9}{25}\\ &= \pm \dfrac{3}{5} \end{align*}\]

Ya que\(\theta={\cos}^{−1}\left (\dfrac{4}{5}\right )\) está en el cuadrante I,\(\sin \theta\) debe ser positivo, entonces la solución es\(35\). Ver Figura\(\PageIndex{11}\).

Figura\(\PageIndex{11}\): Triángulo rectángulo que ilustra que si\(\cos \theta=\dfrac{4}{5}\), entonces\(\sin \theta=\dfrac{3}{5}\)

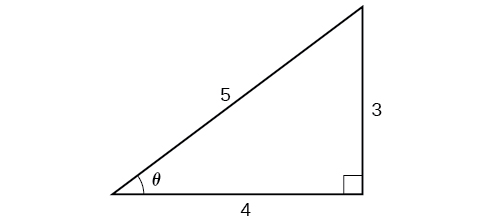
Sabemos que el coseno inverso siempre da un ángulo en el intervalo\([ 0,\pi ]\), por lo que sabemos que el seno de ese ángulo debe ser positivo; por lo tanto\(\sin \left ({\cos}^{−1}\left (\dfrac{4}{5} \right ) \right )=\sin \theta=\dfrac{3}{5}\).

Ejercicio\(\PageIndex{7}\)

Evaluar\(\cos \left ({\tan}^{−1} \left (\dfrac{5}{12} \right ) \right )\).

Contestar

\(\frac{12}{13}\)

Ejemplo\(\PageIndex{8}\): Evaluating the Composition of a Sine with an Inverse Tangent

Encuentra un valor exacto para\(\sin\left({\tan}^{−1}\left(\dfrac{7}{4}\right)\right)\).

Solución

Si bien podríamos usar una técnica similar a la de Ejemplo\(\PageIndex{6}\), aquí demostraremos una técnica diferente. Desde adentro, sabemos que hay un ángulo tal que\(\tan \theta=\dfrac{7}{4}\). Podemos imaginar esto como los lados opuestos y adyacentes en un triángulo rectángulo, como se muestra en la Figura\(\PageIndex{12}\).

Figura\(\PageIndex{12}\): Un triángulo rectángulo con dos lados conocidos

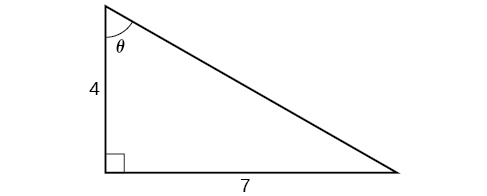
Utilizando el Teorema de Pitágoras, podemos encontrar la hipotenusa de este triángulo.

\ [\ begin {align*}
4^2+7^2&= {hipotenusa} ^2\\
hipotenusa&=\ sqrt {65}
\\\ text {Ahora, podemos evaluar el seno del ángulo como el lado opuesto dividido por la hipotenusa.} \\
\ sin\ theta&=\ dfrac {7} {\ sqrt {65}}\\
\ text {Esto nos da nuestra composición deseada.} \\
\ sin\ izquierda ({\ tan} ^ {-1}\ izquierda (\ dfrac {7} {4}\ derecha)\ derecha) &=\ sin\ theta\\
&=\ dfrac {7} {\ sqrt {65}}\\
&=\ dfrac {7\ sqrt {65}} {65}
\ end {align*}\]

Ejercicio\(\PageIndex{8}\)

Evaluar\(\cos\left({\sin}^{−1}\left(\dfrac{7}{9}\right)\right)\).

Contestar

\(\dfrac{4\sqrt{2}}{9}\)

Ejemplo\(\PageIndex{9}\): Finding the Cosine of the Inverse Sine of an Algebraic Expression

Encuentre una expresión simplificada para\(\cos\left({\sin}^{−1}\left(\dfrac{x}{3}\right)\right)\) for\(−3≤x≤3\).

Solución

Sabemos que hay un ángulo\(\theta\) tal que\(\sin \theta=\dfrac{x}{3}\).

\[\begin{align*} {\sin}^2 \theta+{\cos}^2 \theta&= 1\qquad \text{Use the Pythagorean Theorem}\\ {\left (\dfrac{x}{3}\right )}^2+{\cos}^2 \theta&= 1\qquad \text{Solve for cosine}\\ {\cos}^2 \theta&= 1-\dfrac{x^2}{9}\\ \cos \theta &= \pm \sqrt{\dfrac{9-x^2}{9}}\\ &= \pm \sqrt{\dfrac{9-x^2}{3}} \end{align*}\]

Porque sabemos que el seno inverso debe dar un ángulo en el intervalo\([ −\dfrac{\pi}{2},\dfrac{\pi}{2} ]\), podemos deducir que el coseno de ese ángulo debe ser positivo.

\(cos\left({\sin}^{−1}\left(\dfrac{x}{3}\right)\right)=\sqrt{\dfrac{9-x^2}{3}}\)

Ejercicio\(\PageIndex{9}\)

Encuentre una expresión simplificada para\(\sin({\tan}^{−1}(4x))\) for \(−\dfrac{1}{4}≤x≤\dfrac{1}{4}\).

Contestar

\(\dfrac{4x}{\sqrt{16x^2+1}}\)

Medios

Acceda a este recurso en línea para obtener instrucción y práctica adicional con funciones trigonométricas inversas.

• Evaluar expresiones que involucran funciones trigonométricas inversas

Visite este sitio web para obtener preguntas de práctica adicionales de Learningpod.

Conceptos clave

• Una función inversa es aquella que “deshace” otra función. El dominio de una función inversa es el rango de la función original y el rango de una función inversa es el dominio de la función original.
• Debido a que las funciones trigonométricas no son uno a uno en sus dominios naturales, las funciones trigonométricas inversas se definen para dominios restringidos.
• Para cualquier función trigonométrica\(f(x)\), si\(x=f^{−1}(y)\), entonces\(f(x)=y\). Sin embargo,\(f(x)=y\) sólo implica\(x=f^{−1}(y)\) si\(x\) está en el dominio restringido de\(f\). Ver Ejemplo\(\PageIndex{1}\).
• Los ángulos especiales son las salidas de funciones trigonométricas inversas para valores de entrada especiales; por ejemplo,\(\frac{\pi}{4}={\tan}^{−1}(1)\) y\(\frac{\pi}{6}={\sin}^{−1}(\frac{1}{2})\) .Ver Ejemplo\(\PageIndex{2}\).
• Una calculadora devolverá un ángulo dentro del dominio restringido de la función trigonométrica original. Ver Ejemplo\(\PageIndex{3}\).
• Las funciones inversas nos permiten encontrar un ángulo cuando se dan dos lados de un triángulo rectángulo. Ver Ejemplo\(\PageIndex{4}\).
• En la composición de funciones, si la función interior es una función trigonométrica inversa, entonces hay expresiones exactas; por ejemplo,\(\sin({\cos}^{−1}(x))=\sqrt{1−x^2}\). Ver Ejemplo\(\PageIndex{5}\).
• Si la función interior es una función trigonométrica, entonces las únicas combinaciones posibles son\({\sin}^{−1}(\cos x)=\frac{\pi}{2}−x\) si\(0≤x≤\pi\) y\({\cos}^{−1}(\sin x)=\frac{\pi}{2}−x\) si\(−\frac{\pi}{2}≤x≤\frac{\pi}{2}\). Ver Ejemplo\(\PageIndex{6}\) y Ejemplo\(\PageIndex{7}\).
• Al evaluar la composición de una función trigonométrica con una función trigonométrica inversa, dibuje un triángulo de referencia para ayudar a determinar la relación de lados que representa la salida de la función trigonométrica. Ver Ejemplo\(\PageIndex{8}\).
• Al evaluar la composición de una función trigonométrica con una función trigonométrica inversa, puede usar identidades trigonométricas para ayudar a determinar la proporción de lados. Ver Ejemplo\(\PageIndex{9}\).