12.1: La elipse

Objetivos de aprendizaje

• Escribir ecuaciones de elipses en forma estándar.
• Gráfica elipses centradas en el origen.
• Gráfica elipses no centradas en el origen.
• Resolver problemas aplicados que involucran elipses.

¿Te imaginas parado en un extremo de una habitación grande y aún así poder escuchar un susurro de una persona parada en el otro extremo? El Salón Nacional de Estatuas en Washington, D.C., que se muestra en la Figura$\PageIndex{1}$, es tal habitación. Se trata de una habitación de forma ovalada llamada cámara susurrante porque la forma hace posible que el sonido viaje a lo largo de las paredes. En esta sección, investigaremos la forma de esta sala y sus aplicaciones del mundo real, incluyendo hasta qué punto de distancia pueden pararse dos personas en el Salón de Estatuas y aún se escuchan susurrar.

Figura$\PageIndex{1}$: El Salón Nacional de Estatuas en Washington, D.C. (crédito: Greg Palmer, Flickr)

Escribir ecuaciones de elipses en forma estándar

Una sección cónica, o cónica, es una forma resultante de la intersección de un cono circular derecho con un plano. El ángulo en el que el plano cruza el cono determina la forma, como se muestra en la Figura$\PageIndex{2}$.

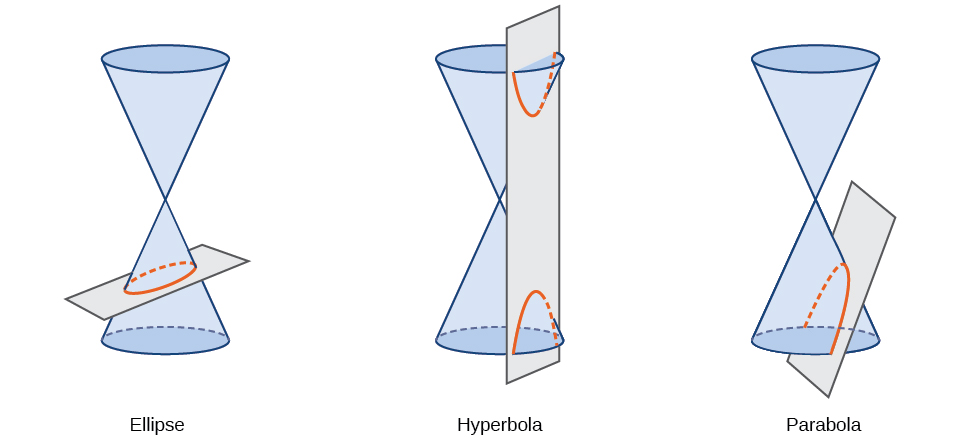
Figura$\PageIndex{2}$

Las secciones cónicas también se pueden describir mediante un conjunto de puntos en el plano de coordenadas. Posteriormente en este capítulo, veremos que la gráfica de cualquier ecuación cuadrática en dos variables es una sección cónica. Los signos de las ecuaciones y los coeficientes de los términos variables determinan la forma. Esta sección se centra en las cuatro variaciones de la forma estándar de la ecuación para la elipse. Una elipse es el conjunto de todos los puntos$(x,y)$ en un plano tal que la suma de sus distancias desde dos puntos fijos es una constante. Cada punto fijo se llama foco (plural: focos).

Podemos dibujar una elipse usando un trozo de cartón, dos tachuelas, un lápiz y una cuerda. Coloca las tachuelas en el cartón para formar los focos de la elipse. Cortar un trozo de cuerda más largo que la distancia entre las dos tachuelas (la longitud de la cuerda representa la constante en la definición). Pegue cada extremo de la cuerda al cartón y trace una curva con un lápiz tenso contra la cuerda. El resultado es una elipse. Ver Figura$\PageIndex{3}$.

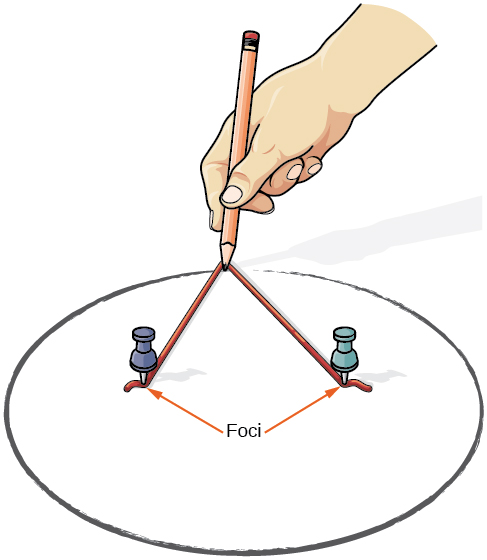
Figura$\PageIndex{3}$

Cada elipse tiene dos ejes de simetría. El eje más largo se llama eje mayor, y el eje más corto se llama eje menor. Cada punto final del eje mayor es el vértice de la elipse (plural: vértices), y cada punto final del eje menor es un covértice de la elipse. El centro de una elipse es el punto medio de los ejes mayor y menor. Los ejes son perpendiculares en el centro. Los focos siempre se encuentran en el eje mayor, y la suma de las distancias desde los focos a cualquier punto de la elipse (la suma constante) es mayor que la distancia entre los focos (Figura$\PageIndex{4}$).

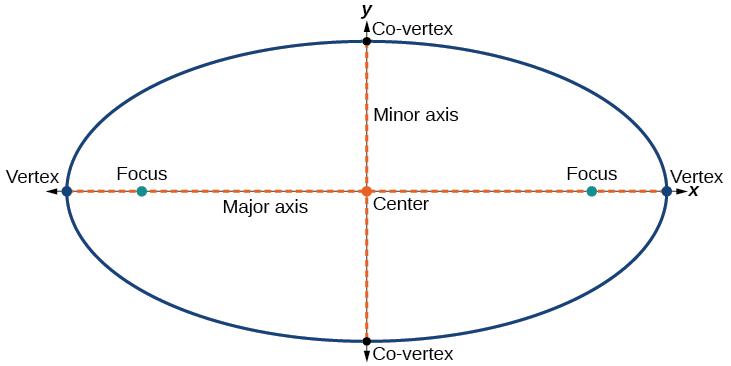
Figura$\PageIndex{4}$

En esta sección, restringimos elipses a aquellas que se posicionan vertical u horizontalmente en el plano de coordenadas. Es decir, los ejes quedarán sobre o serán paralelos a los ejes$x$ - y$y$ -ejes. Más adelante en el capítulo, veremos elipses que se rotan en el plano de coordenadas.

Para trabajar con elipses horizontales y verticales en el plano de coordenadas, consideramos dos casos: los que están centrados en el origen y los que están centrados en un punto distinto al origen. Primero aprenderemos a derivar las ecuaciones de elipses, y luego aprenderemos a escribir las ecuaciones de elipses en forma estándar. Posteriormente utilizaremos lo que aprendamos para dibujar las gráficas.

Derivar la ecuación de una elipse centrada en el origen

Para derivar la ecuación de una elipse centrada en el origen, comenzamos con los focos$(−c,0)$ y$(c,0)$. La elipse es el conjunto de todos los puntos de$(x,y)$ tal manera que la suma de las distancias desde$(x,y)$ a los focos es constante, como se muestra en la Figura$\PageIndex{5}$.

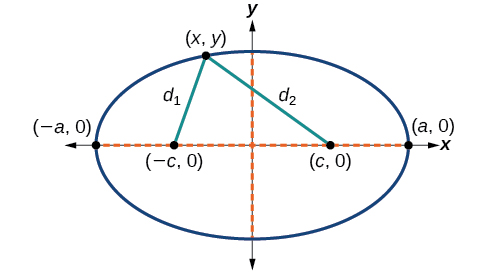
Figura$\PageIndex{5}$

Si$(a,0)$ es un vértice de la elipse, la distancia de$(−c,0)$ a$(a,0)$ es$a−(−c)=a+c$. La distancia de$(c,0)$ a$(a,0)$ es$a−c$. La suma de las distancias desde los focos hasta el vértice es

$(a+c)+(a−c)=2a$

Si$(x,y)$ es un punto en la elipse, entonces podemos definir las siguientes variables:

• $d_1=$la distancia de$(−c,0)$ a$(x,y)$
• $d_2=$la distancia de$(c,0)$ a$(x,y)$

Por la definición de elipse,$d_1+d_2$ es constante para cualquier punto$(x,y)$ de la elipse. Sabemos que la suma de estas distancias es$2a$ para el vértice$(a,0)$. De ello se deduce que$d_1+d_2=2a$ para cualquier punto de la elipse. Comenzaremos la derivación aplicando la fórmula de distancia. El resto de la derivación es algebraica.

$$\begin{align*} d_1+d_2&= 2a\\ \sqrt{{(x-(-c))}^2+{(y-0)}^2}+\sqrt{{(x-c)}^2+{(y-0)}^2}&=2a\qquad \text{Distance formula}\\ \sqrt{{(x+c)}^2+y^2}+\sqrt{{(x-c)}^2+y^2}&=2a\qquad \text{Simplify expressions.}\\ \sqrt{{(x+c)}^2+y^2}&=2a-\sqrt{{(x-c)}^2+y^2}\qquad \text{Move radical to opposite side.}\\ {(x+c)}^2+y^2&={\left[2a-\sqrt{{(x-c)}^2+y^2}\right]}^2\qquad \text{Square both sides.}\\ x^2+2cx+c^2+y^2&=4a^2-4a\sqrt{{(x-c)}^2+y^2}+{(x-c)}^2+y^2\qquad \text{Expand the squares.}\\ x^2+2cx+c^2+y^2&=4a^2-4a\sqrt{{(x-c)}^2+y^2}+x^2-2cx+c^2+y^2\qquad \text{Expand remaining squares.}\\ 2cx&=4a^2-4a\sqrt{{(x-c)}^2+y^2}-2cx\qquad \text{Combine like terms.}\\ 4cx-4a^2&=-4a\sqrt{{(x-c)}^2+y^2}\qquad \text{Isolate the radical.}\\ cx-a^2&=-a\sqrt{{(x-c)}^2+y^2}\qquad \text{Divide by 4.}\\ {\left[ cx-a^2\right]}^2&=a^2{\left[ \sqrt{{(x-c)}^2+y^2}\right] }^2\qquad \text{Square both sides.}\\ c^2x^2-2a^2cx+a^4&=a^2(x^2-2cx+c^2+y^2)\qquad \text{Expand the squares.}\\ c^2x^2-2a^2cx+a^4&=a^2x^2-2a^2cx+a^2c^2+a^2y^2\qquad \text{Distribute } a^2\\ a^2x^2-c^2x^2+a^2y^2&=a^4-a^2c^2\qquad \text{Rewrite.}\\ x^2(a^2-c^2)+a^2y^2&=a^2(a^2-c^2)\qquad \text{Factor common terms.}\\ x^2b^2+a^2y^2&=a^2b^2\qquad \text{Set } b^2=a^2-c^2\\ \dfrac{x^2b^2}{a^2b^2}+\dfrac{a^2y^2}{a^2b^2}&=\dfrac{a^2b^2}{a^2b^2}\qquad \text{Divide both sides by } a^2b^2\\ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}&=1\qquad \text{Simplify} \end{align*}$$

Así, la ecuación estándar de una elipse es$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ .Esta ecuación define una elipse centrada en el origen. Si$a>b$, la elipse se estira más en la dirección horizontal, y si$b>a$, la elipse se estira más en la dirección vertical.

Escribir ecuaciones de elipses centradas en el origen en forma estándar

Las formas estándar de ecuaciones nos hablan de las características clave de las gráficas. Tómese un momento para recordar algunas de las formas estándar de ecuaciones con las que hemos trabajado en el pasado: lineal, cuadrática, cúbica, exponencial, logarítmica, etc. Al aprender a interpretar formas estándar de ecuaciones, estamos uniendo la relación entre representaciones algebraicas y geométricas de fenómenos matemáticos.

Las características clave de la elipse son su centro, vértices, comvértices, focos y longitudes y posiciones de los ejes mayor y menor. Al igual que con otras ecuaciones, podemos identificar todas estas características con solo observar la forma estándar de la ecuación. Hay cuatro variaciones de la forma estándar de la elipse. Estas variaciones se categorizan primero por la ubicación del centro (el origen o no el origen), y luego por la posición (horizontal o vertical). Cada uno se presenta junto con una descripción de cómo las partes de la ecuación se relacionan con la gráfica. Interpretar estas partes nos permite formar una imagen mental de la elipse.

FORMAS ESTÁNDAR DE LA ECUACIÓN DE UNA ELIPSE CON CENTRO$(0,0)$

La forma estándar de la ecuación de una elipse con eje central$(0,0)$ y mayor en el$x$ eje es

$$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$$

donde

• $a>b$
• la longitud del eje mayor es$2a$
• las coordenadas de los vértices son$(\pm a,0)$
• la longitud del eje menor es$2b$
• las coordenadas de los co-vértices son$(0,\pm b)$
• las coordenadas de los focos son$(\pm c,0)$, donde$c^2=a^2−b^2$. Ver Figura$\PageIndex{6a}$.

La forma estándar de la ecuación de una elipse con eje central$(0,0)$ y mayor en el$y$ eje es

$$\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1$$

donde

• $a>b$
• la longitud del eje mayor es$2a$
• las coordenadas de los vértices son$(0,\pm a)$
• la longitud del eje menor es$2b$
• las coordenadas de los co-vértices son$(\pm b,0)$
• las coordenadas de los focos son$(0,\pm c)$, donde$c^2=a^2−b^2$. Ver Figura$\PageIndex{6b}$.

Tenga en cuenta que los vértices, co-vértices y focos están relacionados por la ecuación$c^2=a^2−b^2$. Cuando se nos dan las coordenadas de los focos y vértices de una elipse, podemos usar esta relación para encontrar la ecuación de la elipse en forma estándar.

Figura$\PageIndex{6}$: (a) Elipse horizontal con centro$(0,0)$ (b) Elipse vertical con centro$(0,0)$

Cómo: Dados los vértices y focos de una elipse centrada en el origen, escribir su ecuación en forma estándar

1. Determine si el eje principal se encuentra en el eje x o y.
   • Si las coordenadas dadas de los vértices y focos tienen la forma$(\pm a,0)$ y$(\pm c,0)$ respectivamente, entonces el eje mayor es el eje x. Utilice el formulario estándar$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$
   • Si las coordenadas dadas de los vértices y focos tienen la forma$(0,\pm a)$ y$(\pm c,0)$, respectivamente, entonces el eje mayor es el eje y. Utilice el formulario estándar$\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1$
2. Utilice la ecuación$c^2=a^2−b^2$, junto con las coordenadas dadas de los vértices y focos, para resolver para$b^2$.
3. Sustituir los valores por$a^2$ y$b^2$ en la forma estándar de la ecuación determinada en el Paso 1.

Ejemplo$\PageIndex{1}$: Writing the Equation of an Ellipse Centered at the Origin in Standard Form

¿Cuál es la ecuación de forma estándar de la elipse que tiene vértices$(\pm 8,0)$ y focos$(\pm 5,0)$?

Solución

Los focos están en el$x$ eje, por lo que el eje mayor es el$x$ eje -eje. Así, la ecuación tendrá la forma$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$

Los vértices son$(\pm 8,0)$, así$a=8$ y$a^2=64$.

Los focos son$(\pm 5,0)$, así$c=5$ y$c^2=25$.

Sabemos que los vértices y focos están relacionados por la ecuación$c^2=a^2−b^2$. Resolviendo para$b^2$, tenemos:

$$\begin{align*} c^2&=a^2-b^2\\ 25&=64-b^2\qquad \text{Substitute for } c^2 \text{ and } a^2\\ b^2&=39\qquad \text{Solve for } b^2 \end{align*}$$

Ahora sólo necesitamos sustituto$a^2=64$ y$b^2=39$ en la forma estándar de la ecuación. La ecuación de la elipse es$\dfrac{x^2}{64}+\dfrac{y^2}{39}=1$.

Ejercicio$\PageIndex{1}$

¿Cuál es la ecuación de forma estándar de la elipse que tiene vértices$(0,\pm 4)$ y focos$(0,\pm \sqrt{15})$?

Contestar

$x^2+\dfrac{y^2}{16}=1$

Q&A

¿Podemos escribir la ecuación de una elipse centrada en el origen dadas las coordenadas de un solo foco y vértice?

Sí. Las elipses son simétricas, por lo que las coordenadas de los vértices de una elipse centradas alrededor del origen siempre tendrán la forma$(\pm a,0)$ o$(0, \pm a)$. De igual manera, las coordenadas de los focos siempre tendrán la forma$(\pm c,0)$ o$(0, \pm c)$. Sabiendo esto, podemos usar$a$ y$c$ desde los puntos dados, junto con la ecuación$c^2=a^2−b^2$, para encontrar$b^2$.

Escribir ecuaciones de elipses no centradas en el origen

Al igual que las gráficas de otras ecuaciones, se puede traducir la gráfica de una elipse. Si una elipse se traslada$h$ unidades horizontalmente y$k$ unidades verticalmente, el centro de la elipse será$(h,k)$. Esta traducción da como resultado la forma estándar de la ecuación que vimos anteriormente, con$x$ reemplazada por$(x−h)$ e y reemplazada por$(y−k)$.

FORMAS ESTÁNDAR DE LA ECUACIÓN DE UNA ELIPSE CON CENTRO$(H, K)$

La forma estándar de la ecuación de una elipse con eje central$(h, k)$ y mayor paralelos al$x$ eje -eje es

$$\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1$$

donde

• $a>b$
• la longitud del eje mayor es$2a$
• las coordenadas de los vértices son$(h\pm a,k)$
• la longitud del eje menor es$2b$
• las coordenadas de los co-vértices son$(h,k\pm b)$
• las coordenadas de los focos son$(h\pm c,k)$, donde$c^2=a^2−b^2$. Ver Figura$\PageIndex{7a}$.

La forma estándar de la ecuación de una elipse con eje central$(h,k)$ y mayor paralelos al$y$ eje -eje es

$$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1$$

donde

• $a>b$
• la longitud del eje mayor es$2a$
• las coordenadas de los vértices son$(h,k\pm a)$
• la longitud del eje menor es$2b$
• las coordenadas de los co-vértices son$(h\pm b,k)$
• las coordenadas de los focos son$(h,k\pm c)$, donde$c^2=a^2−b^2$. Ver Figura$\PageIndex{7b}$.

Al igual que con las elipses centradas en el origen, las elipses que están centradas en un punto$(h,k)$ tienen vértices, co-vértices y focos que están relacionados por la ecuación$c^2=a^2−b^2$. Podemos usar esta relación junto con las fórmulas de punto medio y distancia para encontrar la ecuación de la elipse en forma estándar cuando se dan los vértices y focos.

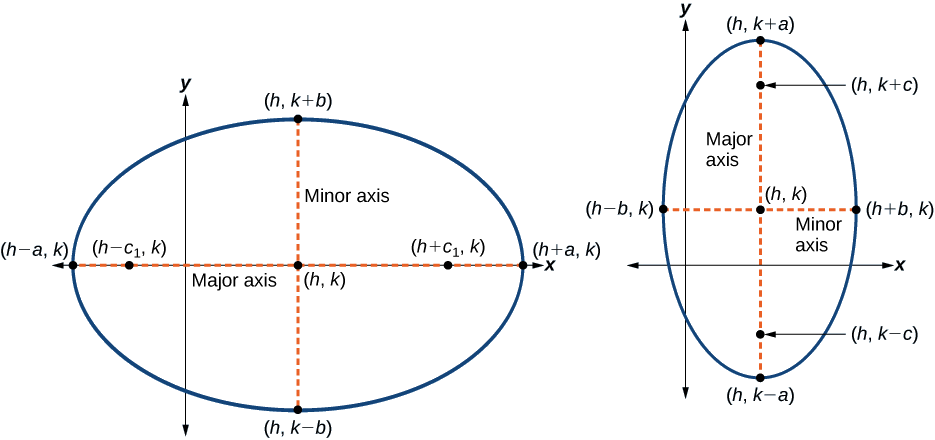
Figura$\PageIndex{7}$: (a) Elipse horizontal con centro$(h,k)$ (b) Elipse vertical con centro$(h,k)$

Cómo: Dados los vértices y focos de una elipse no centrada en el origen, escribir su ecuación en forma estándar

1. Determine si el eje principal es paralelo al eje$x$ - o$y$ -eje.
   • Si las coordenadas y de los vértices y focos dados son las mismas, entonces el eje mayor es paralelo al$x$ eje -eje. Utilice el formulario estándar$\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1$
   • Si las coordenadas x de los vértices y focos dados son las mismas, entonces el eje mayor es paralelo al eje y. Utilice el formulario estándar$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1$
2. Identifica el centro de la elipse$(h,k)$ usando la fórmula de punto medio y las coordenadas dadas para los vértices.
3. Encontrar$a^2$ resolviendo para la longitud del eje mayor,$2a$, que es la distancia entre los vértices dados.
4. Encontrar$c^2$ usando$h$ y$k$, que se encuentra en el Paso 2, junto con las coordenadas dadas para los focos.
5. Resuelve por$b^2$ usar la ecuación$c^2=a^2−b^2$.
6. Sustituir los valores por$h$$k$,$a^2$, y$b^2$ en la forma estándar de la ecuación determinada en el Paso 1.

Ejemplo$\PageIndex{2}$: Writing the Equation of an Ellipse Centered at a Point Other Than the Origin

¿Cuál es la ecuación de forma estándar de la elipse que tiene vértices$(−2,−8)$$(−2,2)$ y y focos$(−2,−7)$ y$(−2,1)$?

Solución

Las$x$ coordenadas -de los vértices y focos son las mismas, por lo que el eje mayor es paralelo al$y$ eje -eje. Así, la ecuación de la elipse tendrá la forma

$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1 \nonumber$

Primero, identificamos el centro,$(h,k)$. El centro está a medio camino entre los vértices,$(−2,−8)$ y$(−2,2)$. Aplicando la fórmula de punto medio, tenemos:

$$\begin{align} (h,k) &=\left(\dfrac{−2+(−2)}{2},\dfrac{−8+2}{2}\right) \nonumber \\ &=(−2,−3) \nonumber \end{align} \nonumber$$

A continuación, nos encontramos$a^2$. La longitud del eje mayor,$2a$, está delimitada por los vértices. Resolvemos$a$ por encontrar la distancia entre las coordenadas y de los vértices.

$$\begin{align} 2a &=2−(−8) \nonumber \\ 2a &=10 \nonumber\\ a&=5 \nonumber \end{align} \nonumber$$

Entonces$a^2=25$.

Ahora nos encontramos$c^2$. Los focos están dados por$(h,k\pm c)$. Entonces,$(h,k−c)=(−2,−7)$ y$(h,k+c)=(−2,1)$. Sustituimos$k=−3$ usando cualquiera de estos puntos para resolver$c$.

$$\begin{align} k+c &=1 \nonumber \\ −3+c&=1 \nonumber \\ c&=4 \nonumber \end{align} \nonumber$$

Entonces$c^2=16$.

A continuación, resolvemos por$b^2$ usar la ecuación$c^2=a^2−b^2$.

$$\begin{align} c^2&=a^2−b^2 \nonumber \\ 16&=25−b^2 \nonumber \\ b^2&=9 \nonumber \end{align} \nonumber$$

Finalmente, sustituimos los valores encontrados para$h$,$k$$a^2$, y$b^2$ en la ecuación de forma estándar por una elipse:

$$\dfrac{{(x+2)}^2}{9}+\dfrac{{(y+3)}^2}{25}=1 \nonumber$$

Ejercicio$\PageIndex{2}$

¿Cuál es la ecuación de forma estándar de la elipse que tiene vértices$(−3,3)$$(5,3)$ y y focos$(1−2\sqrt{3},3)$ y$(1+2\sqrt{3},3)$?

Contestar

$\dfrac{{(x−1)}^2}{16}+\dfrac{{(y−3)}^2}{4}=1 \nonumber$

Gráfica de elipses centradas en el origen

Así como podemos escribir la ecuación para una elipse dada su gráfica, podemos graficar una elipse dada su ecuación. Para graficar elipses centradas en el origen, utilizamos la forma estándar

$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1, a>b$para elipses horizontales

y

$\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1, a>b$para elipses verticales

Cómo: Dada la forma estándar de una ecuación para una elipse centrada en$(0, 0)$, sketch the graph.

1. Utilice las formas estándar de las ecuaciones de una elipse para determinar el eje mayor, vértices, co-vértices y focos.
   • Si la ecuación está en la forma$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$, donde$a>b$, entonces
     • el eje mayor es el$x$ eje -eje
     • las coordenadas de los vértices son$(\pm a,0)$
     • las coordenadas de los co-vértices son$(0,\pm b)$
     • las coordenadas de los focos son$(\pm c,0)$
   • Si la ecuación está en la forma$x^2b^2+y^2a^2=1$, donde$a>b$, entonces
     • el eje mayor es el$y$ eje -eje
     • las coordenadas de los vértices son$(0,\pm a)$
     • las coordenadas de los co-vértices son$(\pm b,0)$
     • las coordenadas de los focos son$(0,\pm c)$
2. Resuelve por$c$ usar la ecuación$c^2=a^2−b^2$.
3. Trace el centro, vértices, co-vértices y focos en el plano de coordenadas y dibuje una curva suave para formar la elipse.

Ejemplo$\PageIndex{3}$: Graphing an Ellipse Centered at the Origin

Grafica la elipse dada por la ecuación,$\dfrac{x^2}{9}+\dfrac{y^2}{25}=1$. Identificar y etiquetar el centro, vértices, co-vértices y focos.

Solución

Primero, determinamos la posición del eje mayor. Porque$25>9$, el eje mayor está en el$y$ eje -eje. Por lo tanto, la ecuación está en la forma$\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1$, dónde$b^2=9$ y$a^2=25$. De ello se deduce que:

• el centro de la elipse es$(0,0)$
• las coordenadas de los vértices son$(0,\pm a)=(0,\pm \sqrt{25})=(0,\pm 5)$
• las coordenadas de los co-vértices son$(\pm b,0)=(\pm 9,0)=(\pm 3,0)$
• las coordenadas de los focos son$(0,\pm c)$, donde$c^2=a^2−b^2$ Resolviendo para$c$, tenemos:

$$\begin{align} c&=\pm \sqrt{a^2−b^2} \nonumber \\ &=\pm \sqrt{25−9} \nonumber\\ &=\pm \sqrt{16} \nonumber\\ &=\pm 4 \nonumber \end{align} \nonumber$$

Por lo tanto, las coordenadas de los focos son$(0,\pm 4)$.

A continuación, trazamos y etiquetamos el centro, vértices, co-vértices y focos, y dibujamos una curva suave para formar la elipse. Ver Figura$\PageIndex{8}$.

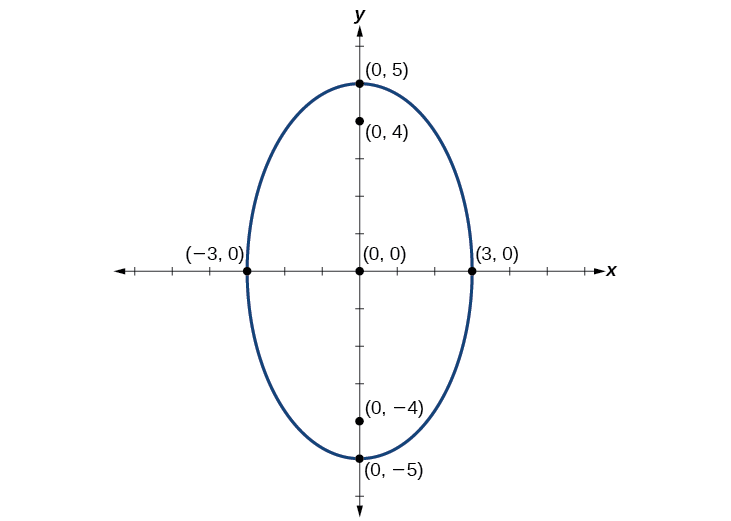
Figura$\PageIndex{8}$

Ejercicio$\PageIndex{3}$

Grafica la elipse dada por la ecuación$\dfrac{x^2}{36}+\dfrac{y^2}{4}=1$. Identificar y etiquetar el centro, vértices, co-vértices y focos.

Contestar

centro:$(0,0)$; vértices:$(\pm 6,0)$; co-vértices:$(0,\pm 2)$; focos:$(\pm 4\sqrt{2},0)$

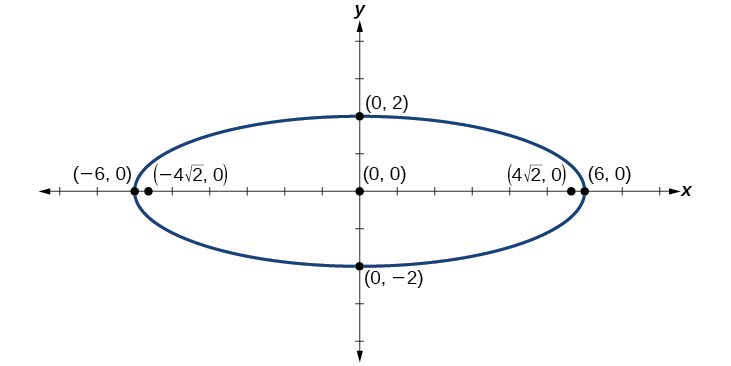
Figura$\PageIndex{9}$

Ejemplo$\PageIndex{4}$: Graphing an Ellipse Centered at the Origin from an Equation Not in Standard Form

Grafica la elipse dada por la ecuación$4x^2+25y^2=100$. Reescribir la ecuación en forma estándar. Luego identifique y etiquete el centro, vértices, co-vértices y focos.

Solución

Primero, use álgebra para reescribir la ecuación en forma estándar.

$$\begin{align} 4x^2+25y^2&=100 \nonumber \\ \dfrac{4x^2}{100}+\dfrac{25y^2}{100}&=\dfrac{100}{100} \nonumber \\ \dfrac{x^2}{25}+\dfrac{y^2}{4}&=1 \nonumber \end{align} \nonumber$$

A continuación, determinamos la posición del eje mayor. Porque$25>4$, el eje mayor está en el$x$ eje -eje. Por lo tanto, la ecuación está en la forma$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$, dónde$a^2=25$ y$b^2=4$. De ello se deduce que:

• el centro de la elipse es$(0,0)$
• las coordenadas de los vértices son$(\pm a,0)=(\pm \sqrt{25},0)=(\pm 5,0)$
• las coordenadas de los co-vértices son$(0,\pm b)=(0,\pm \sqrt{4})=(0,\pm 2)$
• las coordenadas de los focos son$(\pm c,0)$, donde$c^2=a^2−b^2$. Resolviendo para$c$, tenemos:

$$\begin{align} c&=\pm \sqrt{a^2−b^2} \nonumber \\ &=\pm \sqrt{25−4} \nonumber \\ &=\pm \sqrt{21} \nonumber \end{align} \nonumber$$

Por lo tanto las coordenadas de los focos son$(\pm \sqrt{21},0)$.

A continuación, trazamos y etiquetamos el centro, vértices, co-vértices y focos, y dibujamos una curva suave para formar la elipse.

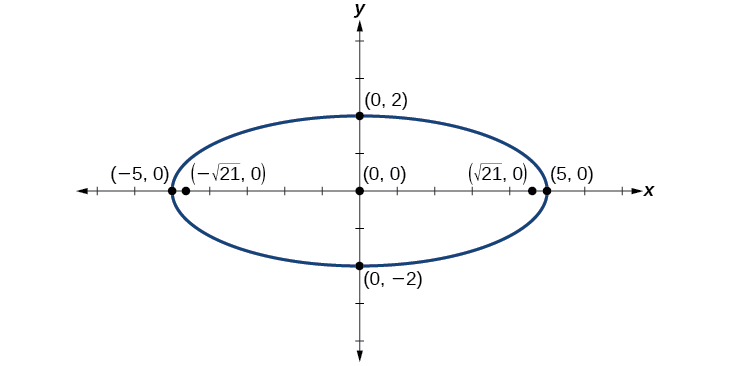
Figura$\PageIndex{10}$

Ejercicio$\PageIndex{4}$

Grafica la elipse dada por la ecuación$49x^2+16y^2=784$. Reescribir la ecuación en forma estándar. Luego identifique y etiquete el centro, vértices, co-vértices y focos.

Contestar

Forma estándar:$\dfrac{x^2}{16}+\dfrac{y^2}{49}=1$; centro:$(0,0)$; vértices:$(0,\pm 7)$; co-vértices:$(\pm 4,0)$; focos:$(0,\pm \sqrt{33})$

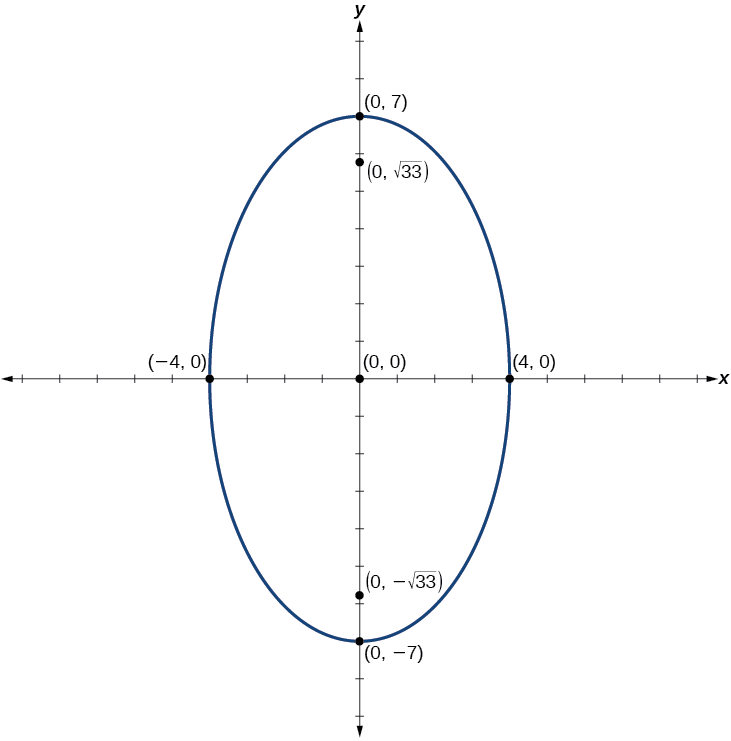
Figura$\PageIndex{11}$

Graficar elipses no centradas en el origen

Cuando una elipse no está centrada en el origen, aún podemos usar las formas estándar para encontrar las características clave de la gráfica. Cuando la elipse está centrada en algún punto,$(h,k)$, utilizamos las formas estándar$\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1$,$a>b$ para elipses horizontales y$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1$,$a>b$ para elipses verticales. A partir de estas ecuaciones estándar, podemos determinar fácilmente el centro, vértices, co-vértices, focos y posiciones de los ejes mayor y menor.

Cómo: Dada la forma estándar de una ecuación para una elipse centrada en$(h, k)$, sketch the graph.

1. Utilice las formas estándar de las ecuaciones de una elipse para determinar el centro, la posición del eje mayor, los vértices, los co-vértices y los focos.
   • Si la ecuación está en la forma$\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1$, donde$a>b$, entonces
     • el centro es$(h,k)$
     • el eje mayor es paralelo al$x$ eje -eje
     • las coordenadas de los vértices son$(h\pm a,k)$
     • las coordenadas de los co-vértices son$(h,k\pm b)$
     • las coordenadas de los focos son$(h\pm c,k)$
   • Si la ecuación está en la forma$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1$, donde$a>b$, entonces
     • el centro es$(h,k)$
     • el eje mayor es paralelo al$y$ eje -eje
     • las coordenadas de los vértices son$(h,k\pm a)$
     • las coordenadas de los co-vértices son$(h\pm b,k)$
     • las coordenadas de los focos son$(h,k\pm c)$
2. Resuelve por$c$ usar la ecuación$c^2=a^2−b^2$.
3. Trace el centro, vértices, co-vértices y focos en el plano de coordenadas y dibuje una curva suave para formar la elipse.

Ejemplo$\PageIndex{5}$: Graphing an Ellipse Centered at $(h, k)$

Grafica la elipse dada por la ecuación,$\dfrac{{(x+2)}^2}{4}+\dfrac{{(y−5)}^2}{9}=1$. Identificar y etiquetar el centro, vértices, co-vértices y focos.

Solución

Primero, determinamos la posición del eje mayor. Porque$9>4$, el eje mayor es paralelo al$y$ eje -eje. Por lo tanto, la ecuación está en la forma$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1$, dónde$b^2=4$ y$a^2=9$. De ello se deduce que:

• el centro de la elipse es$(h,k)=(−2,5)$
• las coordenadas de los vértices son$(h,k\pm a)=(−2,5\pm \sqrt{9})=(−2,5\pm 3)$, o$(−2,2)$ y$(−2,8)$
• las coordenadas de los co-vértices son$(h\pm b,k)=(−2\pm \sqrt{4},5)=(−2\pm 2,5)$, o$(−4,5)$ y$(0,5)$
• las coordenadas de los focos son$(h,k\pm c)$, donde$c^2=a^2−b^2$. Resolviendo para$c$, tenemos:

$$\begin{align} c&=\pm \sqrt{a^2−b^2} \nonumber \\[4pt] &=\pm \sqrt{9−4} \nonumber \\[4pt] &=\pm \sqrt{5} \nonumber \end{align} \nonumber$$

Por lo tanto, las coordenadas de los focos son$(−2,5−\sqrt{5})$ y$(−2,5+\sqrt{5})$.

A continuación, trazamos y etiquetamos el centro, vértices, co-vértices y focos, y dibujamos una curva suave para formar la elipse.

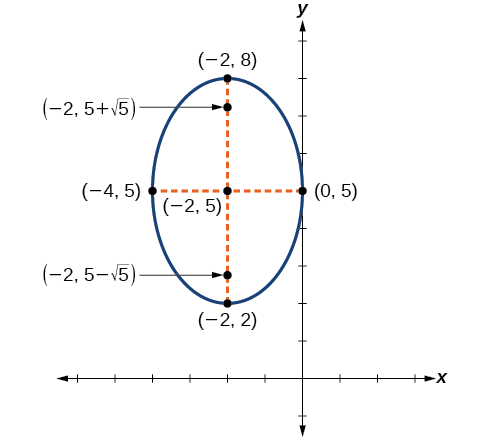
Figura$\PageIndex{12}$

Ejercicio$\PageIndex{5}$

Grafica la elipse dada por la ecuación$\dfrac{{(x−4)}^2}{36}+\dfrac{{(y−2)}^2}{20}=1$. Identificar y etiquetar el centro, vértices, co-vértices y focos.

Contestar

Centro:$(4,2)$; vértices:$(−2,2)$ y$(10,2)$; co-vértices:$(4,2−2\sqrt{5})$ y$(4,2+2\sqrt{5})$; focos:$(0,2)$ y$(8,2)$

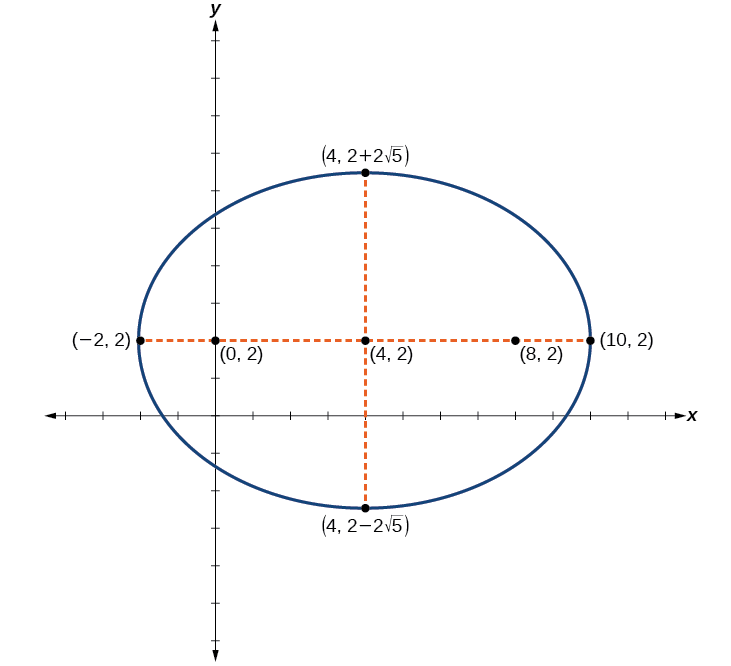
Figura$\PageIndex{13}$

Cómo: Dada la forma general de una ecuación para una elipse centrada en$(h, k)$, express the equation in standard form.

1. Reconocer que una elipse descrita por una ecuación en la forma$ax^2+by^2+cx+dy+e=0$ es en forma general.
2. Reorganice la ecuación agrupando términos que contengan la misma variable. Mover el término constante al lado opuesto de la ecuación.
3. Factorizar los coeficientes de los$x^2$ y$y^2$ términos en preparación para completar el cuadrado.
4. Completar el cuadrado para cada variable para reescribir la ecuación en forma de la suma de múltiplos de dos binomios cuadrados conjunto igual a una constante$m_1{(x−h)}^2+m_2{(y−k)}^2=m_3$,$m_1$, donde$m_2$,, y$m_3$ son constantes.
5. Dividir ambos lados de la ecuación por el término constante para expresar la ecuación en forma estándar.

Ejemplo$\PageIndex{6}$: Graphing an Ellipse Centered at $(h, k)$ by First Writing It in Standard Form

Grafica la elipse dada por la ecuación$4x^2+9y^2−40x+36y+100=0$. Identificar y etiquetar el centro, vértices, co-vértices y focos.

Solución

Debemos comenzar por reescribir la ecuación en forma estándar.

$4x^2+9y^2−40x+36y+100=0$

Agrupe los términos que contienen la misma variable y mueve la constante al lado opuesto de la ecuación.

$(4x^2−40x)+(9y^2+36y)=−100$

Facturar los coeficientes de los términos cuadrados.

$4(x^2−10x)+9(y^2+4y)=−100$

Completa el cuadrado dos veces. Recuerda equilibrar la ecuación sumando las mismas constantes a cada lado.

$4(x^2−10x+25)+9(y^2+4y+4)=−100+100+36$

Reescribe como cuadrados perfectos.

$4{(x−5)}^2+9{(y+2)}^2=36$

Divide ambos lados por el término constante para colocar la ecuación en forma estándar.

$\dfrac{{(x−5)}^2}{9}+\dfrac{{(y+2)}^2}{4}=1$

Ahora que la ecuación está en forma estándar, podemos determinar la posición del eje mayor. Porque$9>4$, el eje mayor es paralelo al$x$ eje -eje. Por lo tanto, la ecuación está en la forma$\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1$, dónde$a^2=9$ y$b^2=4$. De ello se deduce que:

• el centro de la elipse es$(h,k)=(5,−2)$
• las coordenadas de los vértices son$(h\pm a,k)=(5\pm \sqrt{9},−2)=(5\pm 3,−2)$, o$(2,−2)$ y$(8,−2)$
• las coordenadas de los co-vértices son$(h,k\pm b)=(5,−2\pm \sqrt{4})=(5,−2\pm 2)$, o$(5,−4)$ y$(5,0)$
• las coordenadas de los focos son$(h\pm c,k)$, donde$c^2=a^2−b^2$. Resolviendo para$c$, tenemos:

$$\begin{align*} c&=\pm \sqrt{a^2-b^2}\\ &=\pm \sqrt{9-4}\\ &=\pm \sqrt{5} \end{align*}$$

Por lo tanto, las coordenadas de los focos son$(5−\sqrt{5},−2)$ y$(5+\sqrt{5},−2)$.

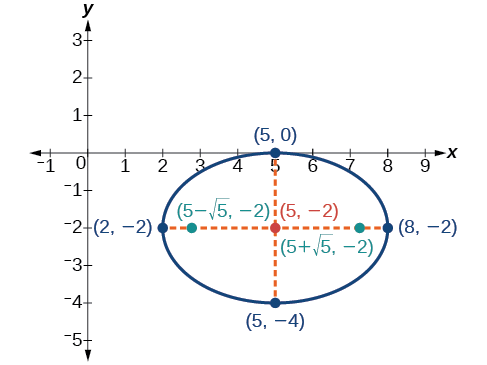
A continuación trazamos y etiquetamos el centro, vértices, co-vértices y focos, y dibujamos una curva suave para formar la elipse como se muestra en la Figura$\PageIndex{14}$.

Figura$\PageIndex{14}$

Ejercicio$\PageIndex{6}$

Expresar la ecuación de la elipse dada en forma estándar. Identificar el centro, vértices, co-vértices y focos de la elipse.

$4x^2+y^2−24x+2y+21=0$

Contestar

$\dfrac{{(x−3)}^2}{4}+\dfrac{{(y+1)}^2}{16}=1$; centro:$(3,−1)$; vértices:$(3,−5)$ y$(3,3)$; co-vértices:$(1,−1)$ y$(5,−1)$; focos:$(3,−1−2\sqrt{3})$ y$(3,−1+2\sqrt{3})$

Solución de problemas aplicados que involucran elipses

Muchas situaciones del mundo real pueden ser representadas por elipses, incluyendo órbitas de planetas, satélites, lunas y cometas, y formas de quillas de barcos, timones y algunas alas de avión. Un dispositivo médico llamado litotriptor utiliza reflectores elípticos para romper los cálculos renales mediante la generación de ondas sonoras. Algunos edificios, llamados cámaras susurrantes, están diseñados con cúpulas elípticas para que una persona susurrando en un foco pueda ser escuchada fácilmente por alguien parado en el otro foco. Esto ocurre debido a las propiedades acústicas de una elipse. Cuando una onda de sonido se origina en un foco de una cámara susurrante, la onda de sonido se reflejará desde la cúpula elíptica y volverá al otro foco (Figura$\PageIndex{15}$). En la cámara de susurros del Museo de Ciencia e Industria en Chicago, dos personas paradas en el foco, a unos$43$ pies de distancia, pueden escucharse susurrar entre sí.

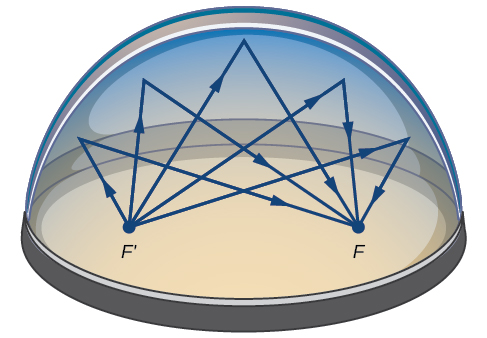
Figura$\PageIndex{15}$: Las ondas sonoras se reflejan entre focos en una habitación elíptica, llamada cámara susurrante.

Ejemplo$\PageIndex{7}$: Locating the Foci of a Whispering Chamber

El Salón Estatuario en el Capitolio en Washington, D.C. es una cámara susurrante. Sus dimensiones son$46$ pies de ancho por$96$ pies de largo como se muestra en la Figura$\PageIndex{16}$.

1. ¿Cuál es la forma estándar de la ecuación de la elipse que representa el contorno de la habitación? Pista: asume una elipse horizontal, y deja que el centro de la habitación sea el punto$(0,0)$.
2. Si dos senadores parados en los focos de esta sala pueden oírse susurrar, ¿a qué distancia están los senadores? Redondear al pie más cercano.

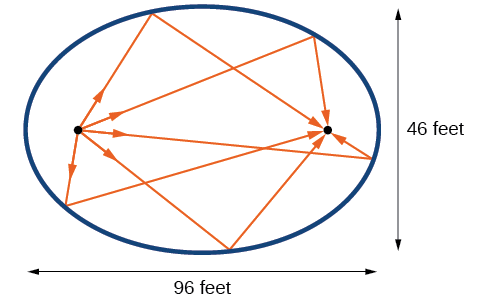
Figura$\PageIndex{16}$

Solución

1. Estamos asumiendo una elipse horizontal con centro$(0,0)$, así que necesitamos encontrar una ecuación de la forma$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$, dónde$a>b$. Sabemos que la longitud del eje mayor,$2a$, es mayor que la longitud del eje menor,$2b$. Por lo que la longitud de la habitación, 96, está representada por el eje mayor, y el ancho de la habitación, 46, está representado por el eje menor.

   Por lo tanto, la ecuación de la elipse es\ [(dfrac {x^2} {2304} +\ dfrac {y^2} {529} =1\)

   • Resolviendo para$a$, tenemos$2a=96$, entonces$a=48$, y$a^2=2304$.
   • Resolviendo para$b$, tenemos$2b=46$, entonces$b=23$, y$b^2=529$.
2. Para encontrar la distancia entre los senadores, debemos encontrar la distancia entre los focos,$(\pm c,0)$, dónde$c^2=a^2−b^2$. Resolviendo para$c$, tenemos:

$$\begin{align*} c^2&=a^2-b^2\\ c^2&=2304-529\qquad \text{Substitute using the values found in part } (a)\\ c&=\pm \sqrt{2304-529}\qquad \text{Take the square root of both sides.}\\ c&=\pm \sqrt{1775}\qquad \text{Subtract.}\\ c&\approx \pm 42\qquad \text{Round to the nearest foot.} \end{align*}$$

Los puntos$(\pm 42,0)$ representan los focos. Así, la distancia entre los senadores es$2(42)=84$ pies.

Ejercicio$\PageIndex{7}$

Supongamos que una cámara susurrante tiene$480$ pies de largo y$320$ pies de ancho.

1. ¿Cuál es la forma estándar de la ecuación de la elipse que representa la habitación? Pista: asume una elipse horizontal, y deja que el centro de la habitación sea el punto$(0,0)$.
2. Si dos personas están paradas en los focos de esta habitación y se escuchan susurrar, ¿a qué distancia está la gente? Redondear al pie más cercano.

Contestar a

$\dfrac{x^2}{57,600}+\dfrac{y^2}{25,600}=1$

Respuesta b

La gente está a$358$ pies de distancia.

Medios

Acceda a estos recursos en línea para obtener instrucción adicional y practicar con elipses.

• Secciones Cónicas: La Elipse
• Grafica una elipse con el centro en el origen
• Grafica una elipse con el centro no en el origen

Ecuaciones Clave

Elipse horizontal, centro en origen	$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$,$a>b$
Elipse vertical, centro en origen	$\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1$,$a>b$
Elipse horizontal, centro$(h,k)$	$\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1$,$a>b$
Elipse vertical, centro$(h,k)$	$\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1$,$a>b$

Key Concepts

• An ellipse is the set of all points $(x,y)$ in a plane such that the sum of their distances from two fixed points is a constant. Each fixed point is called a focus (plural: foci).
• When given the coordinates of the foci and vertices of an ellipse, we can write the equation of the ellipse in standard form. See Example $\PageIndex{1}$ and Example $\PageIndex{2}$.
• When given an equation for an ellipse centered at the origin in standard form, we can identify its vertices, co-vertices, foci, and the lengths and positions of the major and minor axes in order to graph the ellipse. See Example $\PageIndex{3}$ and Example $\PageIndex{4}$.
• When given the equation for an ellipse centered at some point other than the origin, we can identify its key features and graph the ellipse. See Example $\PageIndex{5}$ and Example $\PageIndex{6}$.
• Real-world situations can be modeled using the standard equations of ellipses and then evaluated to find key features, such as lengths of axes and distance between foci. See Example $\PageIndex{7}$.

Contributors and Attributions

• Template:ContribOpenStaxPreCalc