12.2: La hipérbola

Objetivos de aprendizaje

• Localizar los vértices y focos de una hipérbola.
• Escribir ecuaciones de hipérbolas en forma estándar.
• Gráfica hipérbolas centradas en el origen.
• Gráfica hipérbolas no centradas en el origen.
• Resolver problemas aplicados que involucran hipérbolas.

¿Qué tienen en común los caminos de cometas, auges supersónicos, antiguos pilares griegos y torres de enfriamiento de tiro natural? Todos ellos pueden ser modelados por el mismo tipo de cónica. Por ejemplo, cuando algo se mueve más rápido que la velocidad del sonido, se crea una onda de choque en forma de cono. Una porción de una cónica se forma cuando la onda se cruza con el suelo, dando como resultado un boom sónico (Figura\(\PageIndex{1}\)).

Figura\(\PageIndex{1}\): Una onda de choque que cruza el suelo forma una porción de una cónica y da como resultado un boom sónico.

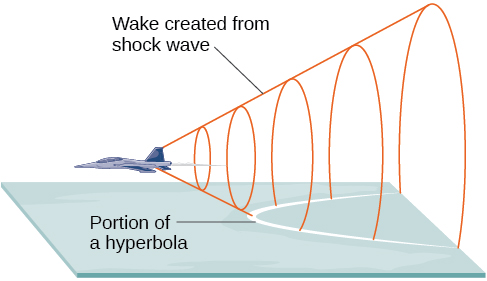
La mayoría de la gente está familiarizada con el boom sónico creado por los aviones supersónicos, pero los humanos estaban rompiendo la barrera del sonido mucho antes del primer vuelo supersónico. La grieta de un látigo se produce porque la punta está superando la velocidad del sonido. Las balas disparadas de muchas armas de fuego también rompen la barrera del sonido, aunque el golpe de la pistola suele reemplazar el sonido del boom sónico.

Localización de los vértices y focos de una hipérbola

En geometría analítica, una hipérbola es una sección cónica formada por la intersección de un cono circular recto con un plano en un ángulo tal que ambas mitades del cono se intersectan. Esta intersección produce dos curvas independientes y no delimitadas que son imágenes especulares entre sí (Figura\(\PageIndex{2}\)).

Figura\(\PageIndex{2}\): Una hipérbola

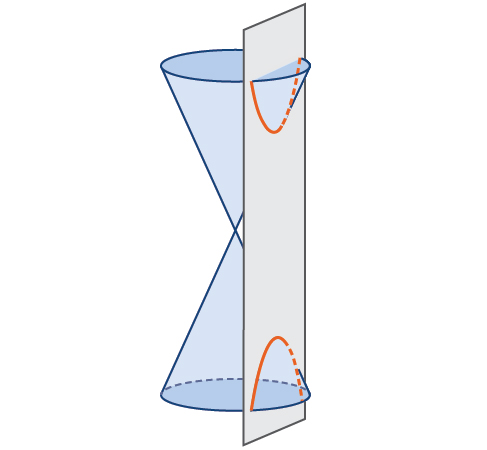
Al igual que la elipse, la hipérbola también se puede definir como un conjunto de puntos en el plano de coordenadas. Una hipérbola es el conjunto de todos los puntos\((x,y)\) en un plano tal que la diferencia de las distancias entre\((x,y)\) y los focos es una constante positiva.

Observe que la definición de una hipérbola es muy similar a la de una elipse. La distinción es que la hipérbola se define en términos de la diferencia de dos distancias, mientras que la elipse se define en términos de la suma de dos distancias.

Al igual que con la elipse, cada hipérbola tiene dos ejes de simetría. El eje transversal es un segmento lineal que pasa por el centro de la hipérbola y tiene vértices como sus extremos. Los focos se encuentran en la línea que contiene el eje transversal. El eje conjugado es perpendicular al eje transversal y tiene los comvértices como sus extremos. El centro de una hipérbola es el punto medio tanto del eje transversal como del eje conjugado, donde se cruzan. Cada hipérbola también tiene dos asíntotas que pasan por su centro. A medida que una hipérbola retrocede del centro, sus ramas se acercan a estas asíntotas. El rectángulo central de la hipérbola está centrado en el origen con lados que pasan por cada vértice y covértice; es una herramienta útil para graficar la hipérbola y sus asíntotas. Para bosquejar las asíntotas de la hipérbola, simplemente dibuje y extienda las diagonales del rectángulo central (Figura\(\PageIndex{3}\)).

Figura\(\PageIndex{3}\): Características clave de la hipérbola

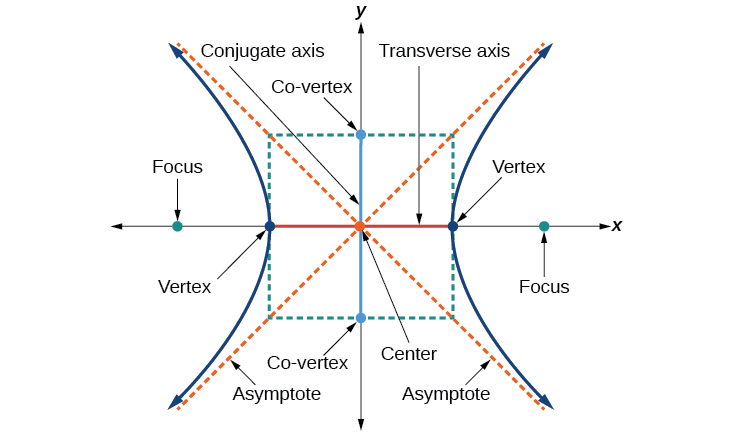
En esta sección, limitaremos nuestra discusión a hipérbolas que se posicionen vertical u horizontalmente en el plano de coordenadas; los ejes se ubicarán o serán paralelos a los ejes\(x\) - y\(y\) -ejes. Consideraremos dos casos: los que están centrados en el origen, y los que están centrados en un punto distinto al origen.

Derivar la ecuación de una elipse centrada en el origen

Dejar\((−c,0)\) y\((c,0)\) ser los focos de una hipérbola centrada en el origen. La hipérbola es el conjunto de todos los puntos\((x,y)\) tal que la diferencia de las distancias de\((x,y)\) a los focos es constante. Ver Figura\(\PageIndex{4}\).

Figura\(\PageIndex{4}\)

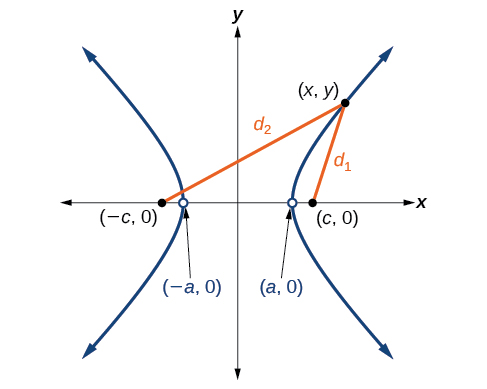
Si\((a,0)\) es un vértice de la hipérbola, la distancia de\((−c,0)\) a\((a,0)\) es\(a−(−c)=a+c\). La distancia de\((c,0)\) a\((a,0)\) es\(c−a\). La suma de las distancias desde los focos hasta el vértice es

\((a+c)−(c−a)=2a\)

Si\((x,y)\) es un punto sobre la hipérbola, podemos definir las siguientes variables:

\(d_2=\)la distancia de\((−c,0)\) a\((x,y)\)

\(d_1=\)la distancia de\((c,0)\) a\((x,y)\)

Por definición de una hipérbola,\(d_2−d_1\) es constante para cualquier punto de\((x,y)\) la hipérbola. Sabemos que la diferencia de estas distancias es\(2a\) para el vértice\((a,0)\). De ello se deduce que\(d_2−d_1=2a\) para cualquier punto sobre la hipérbola. Al igual que con la derivación de la ecuación de una elipse, comenzaremos aplicando la fórmula de distancia. El resto de la derivación es algebraica. Compara esta derivación con la de la sección anterior para elipses.

\[\begin{align*} d_2-d_1&=2a\\ \sqrt{{(x-(-c))}^2+{(y-0)}^2}-\sqrt{{(x-c)}^2+{(y-0)}^2}&=2a\qquad \text{Distance Formula}\\ \sqrt{{(x+c)}^2+y^2}-\sqrt{{(x-c)}^2+y^2}&=2a\qquad \text{Simplify expressions.}\\ \sqrt{{(x+c)}^2+y^2}&=2a+\sqrt{{(x-c)}^2+y^2}\qquad \text{Move radical to opposite side.}\\ {(x+c)}^2+y^2&={(2a+\sqrt{{(x-c)}^2+y^2})}^2\qquad \text{Square both sides.}\\ x^2+2cx+c^2+y^2&=4a^2+4a\sqrt{{(x-c)}^2+y^2}+{(x-c)}^2+y^2\qquad \text{Expand the squares.}\\ x^2+2cx+c^2+y^2&=4a^2+4a\sqrt{{(x-c)}^2+y^2}+x^2-2cx+c^2+y^2\qquad \text{Expand remaining square.}\\ 2cx&=4a^2+4a\sqrt{{(x-c)}^2+y^2}-2cx\qquad \text{Combine like terms.}\\ 4cx-4a^2&=4a\sqrt{{(x-c)}^2+y^2}\qquad \text{Isolate the radical.}\\ cx-a^2&=a\sqrt{{(x-c)}^2+y^2}\qquad \text{Divide by 4.}\\ {(cx-a^2)}^2&=a^2{\left[\sqrt{{(x-c)}^2+y^2}\right]}^2\qquad \text{Square both sides.}\\ c^2x^2-2a^2cx+a^4&=a^2(x^2-2cx+c^2+y^2)\qquad \text{Expand the squares.}\\ c^2x^2-2a^2cx+a^4&=a^2x^2-2a^2cx+a^2c^2+a^2y^2\qquad \text{Distribute } a^2\\ a^4+c^2x^2&=a^2x^2+a^2c^2+a^2y^2\qquad \text{Combine like terms.}\\ c^2x^2-a^2x^2-a^2y^2&=a^2c^2-a^4\qquad \text{Rearrange terms.}\\ x^2(c^2-a^2)-a^2y^2&=a^2(c^2-a^2)\qquad \text{Factor common terms.}\\ x^2b^2-a^2y^2&=a^2b^2\qquad \text{Set } b^2=c^2−a^2\\. \dfrac{x^2b^2}{a^2b^2}-\dfrac{a^2y^2}{a^2b^2}&=\dfrac{a^2b^2}{a^2b^2}\qquad \text{Divide both sides by } a^2b^2\\ \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}&=1\\ \end{align*}\]

Esta ecuación define una hipérbola centrada en el origen con vértices\((\pm a,0)\) y co-vértices\((0,\pm b)\).

FORMAS ESTÁNDAR DE LA ECUACIÓN DE UNA HIPERBOLA\((0,0)\)

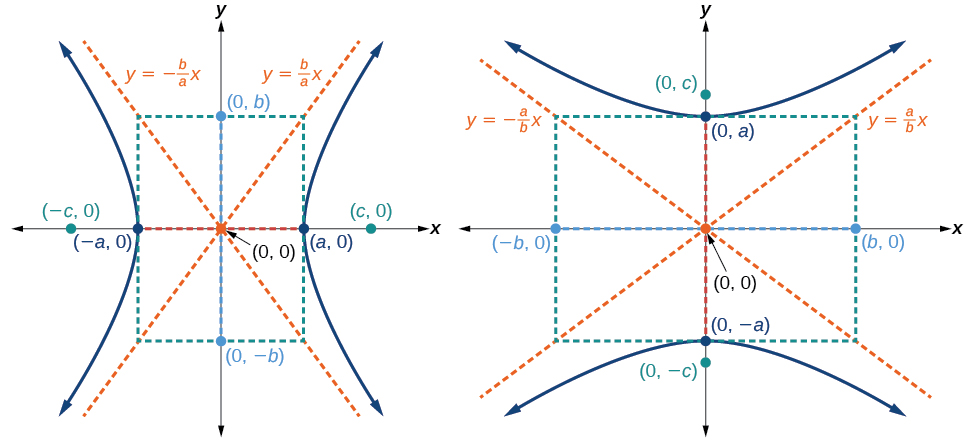
La forma estándar de la ecuación de una hipérbola con eje central\((0,0)\) y transversal en el\(x\) eje es

\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\)

donde

• la longitud del eje transversal es\(2a\)
• las coordenadas de los vértices son\((\pm a,0)\)
• la longitud del eje conjugado es\(2b\)
• las coordenadas de los co-vértices son\((0,\pm b)\)
• la distancia entre los focos es\(2c\), donde\(c^2=a^2+b^2\)
• las coordenadas de los focos son\((\pm c,0)\)
• las ecuaciones de las asíntotas son\(y=\pm \dfrac{b}{a}x\)

Ver Figura\(\PageIndex{5a}\).

La forma estándar de la ecuación de una hipérbola con eje central\((0,0)\) y transversal en el\(y\) eje es

\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\)

donde

• la longitud del eje transversal es\(2a\)
• las coordenadas de los vértices son\((0,\pm a)\)
• la longitud del eje conjugado es\(2b\)
• las coordenadas de los co-vértices son\((\pm b,0)\)
• la distancia entre los focos es\(2c\), donde\(c^2=a^2+b^2\)
• las coordenadas de los focos son\((0,\pm c)\)
• las ecuaciones de las asíntotas son\(y=\pm \dfrac{a}{b}x\)

Ver Figura\(\PageIndex{5b}\).

Tenga en cuenta que los vértices, co-vértices y focos están relacionados por la ecuación\(c^2=a^2+b^2\). Cuando se nos da la ecuación de una hipérbola, podemos usar esta relación para identificar sus vértices y focos.

Figura\(\PageIndex{5}\): (a) Hipérbola horizontal con centro\((0,0)\) (b) Hipérbola vertical con centro\((0,0)\)

Cómo: Dada la ecuación de una hipérbola en forma estándar, ubicar sus vértices y focos

1. Determine si el eje transversal se encuentra en el eje\(x\) - o\(y\) -eje. Observe que siempre\(a^2\) está debajo de la variable con el coeficiente positivo. Entonces, si estableces la otra variable igual a cero, podrás encontrar fácilmente las intercepciones. En el caso de que la hipérbola esté centrada en el origen, las intercepciones coinciden con los vértices.
   • Si la ecuación tiene la forma\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), entonces el eje transversal se encuentra en el\(x\) eje -eje. Los vértices están ubicados en\((\pm a,0)\), y los focos están ubicados en\((\pm c,0)\).
   • Si la ecuación tiene la forma\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\), entonces el eje transversal se encuentra en el\(y\) eje -eje. Los vértices están ubicados en\((0,\pm a)\), y los focos están ubicados en\((0,\pm c)\).
2. Resuelve por\(a\) usar la ecuación\(a=\sqrt{a^2}\).
3. Resuelve por\(c\) usar la ecuación\(c=\sqrt{a^2+b^2}\).

Ejemplo\(\PageIndex{1}\): Locating a Hyperbola’s Vertices and Foci

Identificar los vértices y focos de la hipérbola con ecuación\(\dfrac{y^2}{49}−\dfrac{x^2}{32}=1\).

Solución

La ecuación tiene la forma\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\), por lo que el eje transversal se encuentra en el\(y\) eje -eje. La hipérbola está centrada en el origen, por lo que los vértices sirven como las intercepciones y de la gráfica. Para encontrar los vértices\(x=0\), establecer y resolver para\(y\).

\[\begin{align*} 1&=\dfrac{y^2}{49}-\dfrac{x^2}{32}\\ 1&=\dfrac{y^2}{49}-\dfrac{0^2}{32}\\ 1&=\dfrac{y^2}{49}\\ y^2&=49\\ y&=\pm \sqrt{49}\\ &=\pm 7 \end{align*}\]

Los focos se encuentran en\((0,\pm c)\). Resolviendo para\(c\),

\[\begin{align*} c&=\sqrt{a^2+b^2}\\ &=\sqrt{49+32}\\ &=\sqrt{81}\\ &=9 \end{align*}\]

Por lo tanto, los vértices se localizan en\((0,\pm 7)\), y los focos están ubicados en\((0,9)\).

Ejercicio\(\PageIndex{1}\)

Identificar los vértices y focos de la hipérbola con ecuación\(\dfrac{x^2}{9}−\dfrac{y^2}{25}=1\).

Contestar

Vértices:\((\pm 3,0)\); Focos:\((\pm \sqrt{34},0)\)

Escribir ecuaciones de hipérbolas en forma estándar

Al igual que con las elipses, escribir la ecuación para una hipérbola en forma estándar nos permite calcular las características clave: su centro, vértices, co-vértices, focos, asíntotas, y las longitudes y posiciones de los ejes transversal y conjugado. Por el contrario, se puede encontrar una ecuación para una hipérbola dadas sus características clave. Comenzamos por encontrar ecuaciones estándar para hipérbolas centradas en el origen. Después volveremos nuestra atención a encontrar ecuaciones estándar para hipérbolas centradas en algún punto distinto al origen.

Hipérbolas Centradas en el Origen

Revisando las formas estándar dadas para hipérbolas centradas en\((0,0)\), vemos que los vértices, co-vértices y focos están relacionados por la ecuación\(c^2=a^2+b^2\). Tenga en cuenta que esta ecuación también se puede reescribir como\(b^2=c^2−a^2\). Esta relación se utiliza para escribir la ecuación para una hipérbola cuando se dan las coordenadas de sus focos y vértices.

Cómo: Dados los vértices y focos de una hipérbola centrada en\((0,0)\), write its equation in standard form

1. Determine si el eje transversal se encuentra en el eje\(x\) - o\(y\) -eje.
   • Si las coordenadas dadas de los vértices y focos tienen la forma\((\pm a,0)\) y\((\pm c,0)\), respectivamente, entonces el eje transversal es el eje\(x\) -eje. Utilice el formulario estándar\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\).
   • Si las coordenadas dadas de los vértices y focos tienen la forma\((0,\pm a)\) y\((0,\pm c)\), respectivamente, entonces el eje transversal es el eje\(y\) -eje. Utilice el formulario estándar\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\).
2. Encuentra\(b^2\) usando la ecuación\(b^2=c^2−a^2\).
3. Sustituir los valores por\(a^2\) y\(b^2\) en la forma estándar de la ecuación determinada en el Paso 1.

Ejemplo\(\PageIndex{2}\): Finding the Equation of a Hyperbola Centered at \((0,0)\) Given its Foci and Vertices

¿Cuál es la ecuación de forma estándar de la hipérbola que tiene vértices\((\pm 6,0)\) y focos\((\pm 2\sqrt{10},0)\)?

Solución

Los vértices y focos están en el\(x\) eje. Así, la ecuación para la hipérbola tendrá la forma\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\).

Los vértices son\((\pm 6,0)\), así\(a=6\) y\(a^2=36\).

Los focos son\((\pm 2\sqrt{10},0)\), así\(c=2\sqrt{10}\) y\(c^2=40\).

Resolviendo para\(b^2\), tenemos

\[\begin{align*} b^2&=c^2-a^2\\ b^2&=40-36\qquad \text{Substitute for } c^2 \text{ and } a^2\\ b^2&=4\qquad \text{Subtract.} \end{align*}\]

Finalmente, sustituimos\(a^2=36\) y\(b^2=4\) en la forma estándar de la ecuación,\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\). La ecuación de la hipérbola es\(\dfrac{x^2}{36}−\dfrac{y^2}{4}=1\), como se muestra en la Figura\(\PageIndex{6}\).

Figura\(\PageIndex{6}\)

Ejercicio\(\PageIndex{2}\)

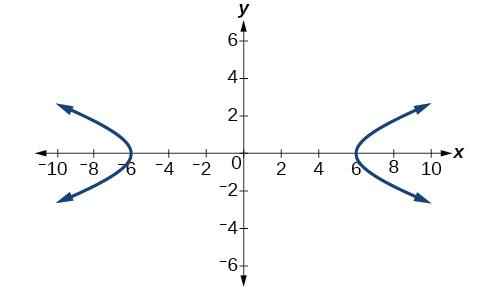
¿Cuál es la ecuación de forma estándar de la hipérbola que tiene vértices\((0,\pm 2)\) y focos\((0,\pm 2\sqrt{5})\)?

Contestar

\(\dfrac{y^2}{4}−\dfrac{x^2}{16}=1\)

Hipérbolas no centradas en el origen

Al igual que las gráficas para otras ecuaciones, se puede traducir la gráfica de una hipérbola. Si una hipérbola se traduce\(h\) unidades horizontalmente y\(k\) unidades verticalmente, el centro de la hipérbola será\((h,k)\). Esta traducción da como resultado la forma estándar de la ecuación que vimos anteriormente, con\(x\) reemplazada por\((x−h)\) y\(y\) reemplazada por\((y−k)\).

FORMAS ESTÁNDAR DE LA ECUACIÓN DE UNA HIPERBOLA\((H, K)\)

La forma estándar de la ecuación de una hipérbola con eje central\((h,k)\) y transversal paralelos al\(x\) eje -es

\[\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\]

donde

• la longitud del eje transversal es\(2a\)
• las coordenadas de los vértices son\((h\pm a,k)\)
• la longitud del eje conjugado es\(2b\)
• las coordenadas de los co-vértices son\((h,k\pm b)\)
• la distancia entre los focos es\(2c\), donde\(c^2=a^2+b^2\)
• las coordenadas de los focos son\((h\pm c,k)\)

Las asíntotas de la hipérbola coinciden con las diagonales del rectángulo central. La longitud del rectángulo es\(2a\) y su anchura es\(2b\). Las pendientes de las diagonales son\(\pm \dfrac{b}{a}\), y cada diagonal pasa por el centro\((h,k)\). Usando la fórmula punto-pendiente, es sencillo mostrar que las ecuaciones de las asíntotas son\(y=\pm \dfrac{b}{a}(x−h)+k\). Ver Figura\(\PageIndex{7a}\).

La forma estándar de la ecuación de una hipérbola con eje central\((h,k)\) y transversal paralelos al\(y\) eje -es

\[\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\]

donde

• la longitud del eje transversal es\(2a\)
• las coordenadas de los vértices son\((h,k\pm a)\)
• la longitud del eje conjugado es\(2b\)
• las coordenadas de los co-vértices son\((h\pm b,k)\)
• la distancia entre los focos es\(2c\), donde\(c^2=a^2+b^2\)
• las coordenadas de los focos son\((h,k\pm c)\)

Utilizando el razonamiento anterior, las ecuaciones de las asíntotas son\(y=\pm \dfrac{a}{b}(x−h)+k\). Ver Figura\(\PageIndex{7b}\).

Figura\(\PageIndex{7}\): (a) Hipérbola horizontal con centro\((h,k)\) (b) Hipérbola vertical con centro\((h,k)\)

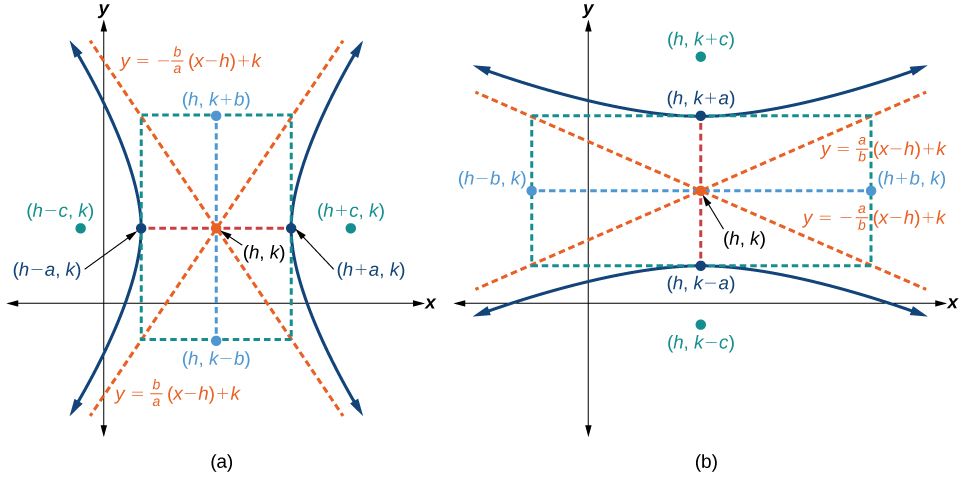
Al igual que las hipérbolas centradas en el origen, las hipérbolas centradas en un punto\((h,k)\) tienen vértices, co-vértices y focos que están relacionados por la ecuación\(c^2=a^2+b^2\). Podemos usar esta relación junto con las fórmulas de punto medio y distancia para encontrar la ecuación estándar de una hipérbola cuando se dan los vértices y focos.

Cómo: Dados los vértices y focos de una hipérbola centrada en\((h,k)\),write its equation in standard form

1. Determine si el eje transversal es paralelo al eje\(x\) - o\(y\) -eje.
   • Si las\(y\) coordenadas -de los vértices y focos dados son las mismas, entonces el eje transversal es paralelo al\(x\) eje -eje. Utilice el formulario estándar\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\).
   • Si las\(x\) coordenadas -de los vértices y focos dados son las mismas, entonces el eje transversal es paralelo al\(y\) eje -eje. Utilice el formulario estándar\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\).
2. Identificar el centro de la hipérbola\((h,k)\), usando la fórmula de punto medio y las coordenadas dadas para los vértices.
3. Encontrar\(a^2\) resolviendo para la longitud del eje transversal,\(2a\), que es la distancia entre los vértices dados.
4. Encuentra\(c^2\) usando\(h\) y\(k\) encontrado en el Paso 2 junto con las coordenadas dadas para los focos.
5. Resuelve por\(b^2\) usar la ecuación\(b^2=c^2−a^2\).
6. Sustituir los valores por\(h\)\(k\),\(a^2\), y\(b^2\) en la forma estándar de la ecuación determinada en el Paso 1.

Ejemplo\(\PageIndex{3}\): Finding the Equation of a Hyperbola Centered at \((h, k)\) Given its Foci and Vertices

¿Cuál es la ecuación de forma estándar de la hipérbola que tiene vértices en\((0,−2)\)\((6,−2)\) y y focos en\((−2,−2)\) y\((8,−2)\)?

Solución

Las\(y\) coordenadas -de los vértices y focos son las mismas, por lo que el eje transversal es paralelo al\(x\) eje -eje. Así, la ecuación de la hipérbola tendrá la forma

\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\)

Primero, identificamos el centro,\((h,k)\). El centro está a medio camino entre los vértices\((0,−2)\) y\((6,−2)\). Aplicando la fórmula de punto medio, tenemos

\((h,k)=(\dfrac{0+6}{2},\dfrac{−2+(−2)}{2})=(3,−2)\)

A continuación, nos encontramos\(a^2\). La longitud del eje transversal,\(2a\), está delimitada por los vértices. Entonces, podemos encontrar\(a^2\) encontrando la distancia entre las\(x\) coordenadas -de los vértices.

\[\begin{align*} 2a&=| 0-6 |\\ 2a&=6\\ a&=3\\ a^2&=9 \end{align*}\]

Ahora tenemos que encontrar\(c^2\). Las coordenadas de los focos son\((h\pm c,k)\). Entonces\((h−c,k)=(−2,−2)\) y\((h+c,k)=(8,−2)\). Podemos usar la\(x\) coordenada -desde cualquiera de estos puntos para resolver para\(c\). Usando el punto\((8,−2)\), y sustituyendo\(h=3\),

\[\begin{align*} h+c&=8\\ 3+c&=8\\ c&=5\\ c^2&=25 \end{align*}\]

A continuación, resuelva para\(b^2\) usar la ecuación\(b^2=c^2−a^2\):

\[\begin{align*} b^2&=c^2-a^2\\ &=25-9\\ &=16 \end{align*}\]

Finalmente, sustituya los valores encontrados para\(h\)\(k\),\(a^2\), y\(b^2\) en la forma estándar de la ecuación.

\(\dfrac{{(x−3)}^2}{9}−\dfrac{{(y+2)}^2}{16}=1\)

Ejercicio\(\PageIndex{3}\)

¿Cuál es la ecuación de forma estándar de la hipérbola que tiene vértices\((1,−2)\)\((1,8)\) y y focos\((1,−10)\) y\((1,16)\)?

Contestar

\(\dfrac{{(y−3)}^2}{25}+\dfrac{{(x−1)}^2}{144}=1\)

Graficar hipérbolas centradas en el origen

Cuando tenemos una ecuación en forma estándar para una hipérbola centrada en el origen, podemos interpretar sus partes para identificar las características clave de su gráfica: el centro, vértices, co-vértices, asíntotas, focos, y longitudes y posiciones de los ejes transversal y conjugado. Para graficar hipérbolas centradas en el origen, utilizamos la forma estándar\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\) para hipérbolas horizontales y la forma estándar\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\) para hipérbolas verticales.

Cómo: Dada una ecuación de forma estándar para una hipérbola centrada en\((0,0)\), sketch the graph

1. Determinar cuál de las formas estándar se aplica a la ecuación dada.
2. Utilice la forma estándar identificada en el Paso 1 para determinar la posición del eje transversal; las coordenadas para los vértices, co-vértices y focos; y las ecuaciones para las asíntotas.
   • Si la ecuación está en la forma\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), entonces
     • el eje transversal está en el\(x\) eje
     • las coordenadas de los vértices son\ ((\ pm a,0)\ 0
     • las coordenadas de los co-vértices son\((0,\pm b)\)
     • las coordenadas de los focos son\((\pm c,0)\)
     • las ecuaciones de las asíntotas son\(y=\pm \dfrac{b}{a}x\)
   • Si la ecuación está en la forma\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\), entonces
     • el eje transversal está en el\(y\) eje
     • las coordenadas de los vértices son\((0,\pm a)\)
     • las coordenadas de los co-vértices son\((\pm b,0)\)
     • las coordenadas de los focos son\((0,\pm c)\)
     • las ecuaciones de las asíntotas son\(y=\pm \dfrac{a}{b}x\)
3. Resuelve las coordenadas de los focos usando la ecuación\(c=\pm \sqrt{a^2+b^2}\).
4. Trace los vértices, co-vértices, focos y asíntotas en el plano de coordenadas y dibuje una curva suave para formar la hipérbola.

Ejemplo\(\PageIndex{4}\): Graphing a Hyperbola Centered at \((0,0)\) Given an Equation in Standard Form

Grafica la hipérbola dada por la ecuación\(\dfrac{y^2}{64}−\dfrac{x^2}{36}=1\). Identificar y etiquetar los vértices, co-vértices, focos y asíntotas.

Solución

La forma estándar que se aplica a la ecuación dada es\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\). Así, el eje transversal está en el\(y\) eje -eje

Las coordenadas de los vértices son\((0,\pm a)=(0,\pm \sqrt{64})=(0,\pm 8)\)

Las coordenadas de los co-vértices son\((\pm b,0)=(\pm \sqrt{36}, 0)=(\pm 6,0)\)

Las coordenadas de los focos son\((0,\pm c)\), donde\(c=\pm \sqrt{a^2+b^2}\). Resolviendo para\(c\), tenemos

\(c=\pm \sqrt{a^2+b^2}=\pm \sqrt{64+36}=\pm \sqrt{100}=\pm 10\)

Por lo tanto, las coordenadas de los focos son\((0,\pm 10)\)

Las ecuaciones de las asíntotas son\(y=\pm \dfrac{a}{b}x=\pm \dfrac{8}{6}x=\pm \dfrac{4}{3}x\)

Trace y etiquete los vértices y co-vértices, y luego dibuje el rectángulo central. Los lados del rectángulo son paralelos a los ejes y pasan a través de los vértices y co-vértices. Esboza y extiende las diagonales del rectángulo central para mostrar las asíntotas. El rectángulo central y las asíntotas proporcionan el marco necesario para esbozar una gráfica precisa de la hipérbola. Marcar los focos y asíntotas, y dibujar una curva suave para formar la hipérbola, como se muestra en la Figura\(\PageIndex{8}\).

Figura\(\PageIndex{8}\)

Ejercicio\(\PageIndex{4}\)

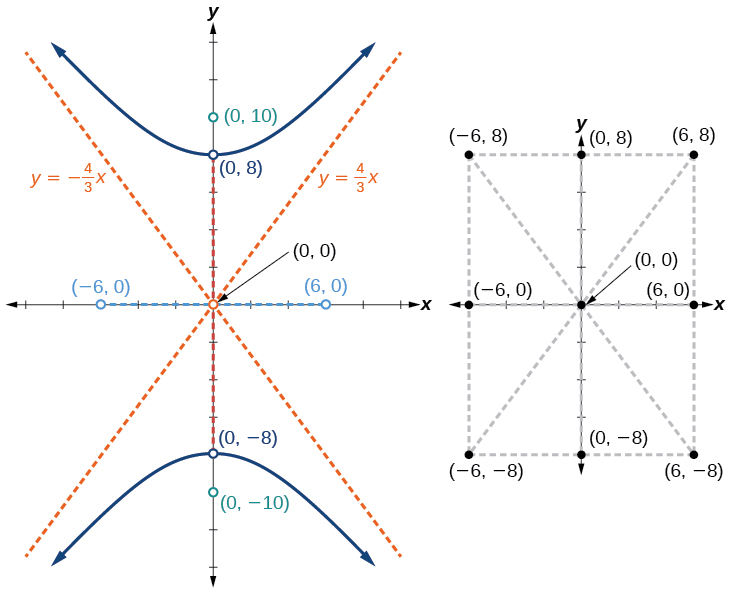
Grafica la hipérbola dada por la ecuación\(\dfrac{x^2}{144}−\dfrac{y^2}{81}=1\). Identificar y etiquetar los vértices, co-vértices, focos y asíntotas.

Contestar

vértices:\((\pm 12,0)\); co-vértices:\((0,\pm 9)\); focos:\((\pm 15,0)\); asíntotas:\(y=\pm \dfrac{3}{4}x\);

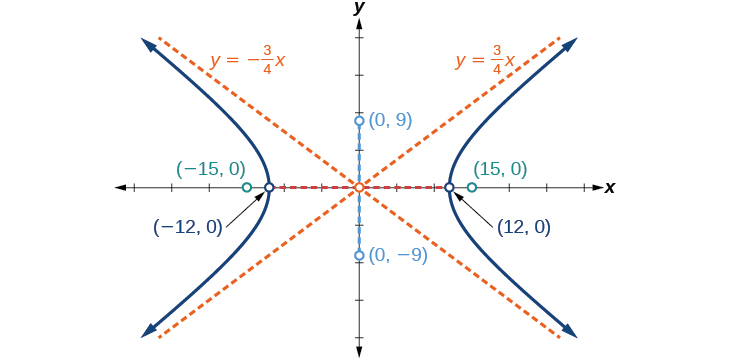
Figura\(\PageIndex{9}\)

Graficar hipérbolas no centradas en el origen

Graficar hipérbolas centradas en un punto\((h,k)\) distinto del origen es similar a trazar elipses centradas en un punto distinto del origen. Utilizamos las formas estándar\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\) para hipérbolas horizontales y\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\) para hipérbolas verticales. A partir de estas ecuaciones de forma estándar podemos calcular y trazar fácilmente las características clave de la gráfica: las coordenadas de su centro, vértices, co-vértices y focos; las ecuaciones de sus asíntotas; y las posiciones de los ejes transversal y conjugado.

Cómo: Dada una forma general para una hipérbola centrada en\((h, k)\), sketch the graph

1. Convertir la forma general a esa forma estándar. Determinar cuál de las formas estándar se aplica a la ecuación dada.
2. Utilice la forma estándar identificada en el Paso 1 para determinar la posición del eje transversal; las coordenadas para el centro, vértices, co-vértices, focos; y ecuaciones para las asíntotas.
   1. Si la ecuación está en la forma\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\), entonces
      • el eje transversal es paralelo al\(x\) eje -eje
      • el centro es\((h,k)\)
      • las coordenadas de los vértices son\((h\pm a,k)\)
      • las coordenadas de los co-vértices son\((h,k\pm b)\)
      • las coordenadas de los focos son\((h\pm c,k)\)
      • las ecuaciones de las asíntotas son\(y=\pm \dfrac{b}{a}(x−h)+k\)
   2. Si la ecuación está en la forma\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\), entonces
      • el eje transversal es paralelo al\(y\) eje -eje
      • el centro es\((h,k)\)
      • las coordenadas de los vértices son\((h,k\pm a)\)
      • las coordenadas de los co-vértices son\((h\pm b,k)\)
      • las coordenadas de los focos son\((h,k\pm c)\)
      • las ecuaciones de las asíntotas son\(y=\pm \dfrac{a}{b}(x−h)+k\)
3. Resuelve las coordenadas de los focos usando la ecuación\(c=\pm \sqrt{a^2+b^2}\).
4. Trace el centro, vértices, co-vértices, focos y asíntotas en el plano de coordenadas y dibuje una curva suave para formar la hipérbola.

Ejemplo\(\PageIndex{5}\): Graphing a Hyperbola Centered at \((h, k)\) Given an Equation in General Form

Grafica la hipérbola dada por la ecuación\(9x^2−4y^2−36x−40y−388=0\). Identificar y etiquetar el centro, vértices, co-vértices, focos y asíntotas.

Solución

Comience expresando la ecuación en forma estándar. Agrupe los términos que contengan la misma variable, y mueva la constante al lado opuesto de la ecuación.

\((9x^2−36x)−(4y^2+40y)=388\)

Factorice el coeficiente principal de cada expresión.

\(9(x^2−4x)−4(y^2+10y)=388\)

Completa el cuadrado dos veces. Recuerda equilibrar la ecuación sumando las mismas constantes a cada lado.

\(9(x^2−4x+4)−4(y^2+10y+25)=388+36−100\)

Reescribe como cuadrados perfectos.

\(9{(x−2)}^2−4{(y+5)}^2=324\)

Divide ambos lados por el término constante para colocar la ecuación en forma estándar.

\(\dfrac{{(x−2)}^2}{36}−\dfrac{{(y+5)}^2}{81}=1\)

La forma estándar que se aplica a la ecuación dada es\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\), dónde\(a^2=36\) y\(b^2=81\), o\(a=6\) y\(b=9\). Así, el eje transversal es paralelo al\(x\) eje -eje. De ello se deduce que:

el centro de la elipse es\((h,k)=(2,−5)\)

las coordenadas de los vértices son\((h\pm a,k)=(2\pm 6,−5)\), o\((−4,−5)\) y\((8,−5)\)

las coordenadas de los co-vértices son\((h,k\pm b)=(2,−5\pm 9)\), o\((2,−14)\) y\((2,4)\)

las coordenadas de los focos son\((h\pm c,k)\), donde\(c=\pm \sqrt{a^2+b^2}\). Resolviendo para\(c\), tenemos

\(c=\pm \sqrt{36+81}=\pm \sqrt{117}=\pm 3\sqrt{13}\)

Por lo tanto, las coordenadas de los focos son\((2−3\sqrt{13},−5)\) y\((2+3\sqrt{13},−5)\).

Las ecuaciones de las asíntotas son\(y=\pm \dfrac{b}{a}(x−h)+k=\pm \dfrac{3}{2}(x−2)−5\).

A continuación, trazamos y etiquetamos el centro, vértices, co-vértices, focos y asíntotas y dibujamos curvas suaves para formar la hipérbola, como se muestra en la Figura\(\PageIndex{10}\).

Figura\(\PageIndex{10}\)

Ejercicio\(\PageIndex{5}\)

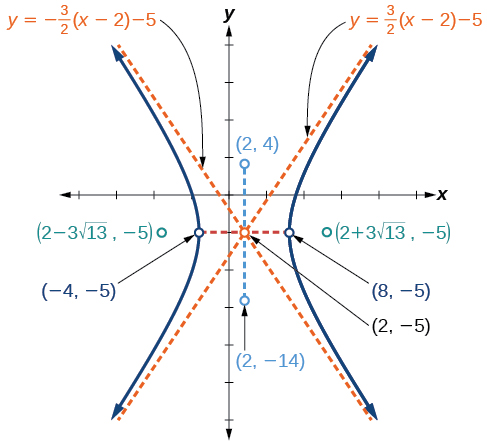
Grafica la hipérbola dada por la forma estándar de una ecuación\(\dfrac{{(y+4)}^2}{100}−\dfrac{{(x−3)}^2}{64}=1\). Identificar y etiquetar el centro, vértices, co-vértices, focos y asíntotas.

Contestar

centro:\((3,−4)\); vértices:\((3,−14)\) y\((3,6)\); co-vértices:\((−5,−4)\); y\((11,−4)\); focos:\((3,−4−2\sqrt{41})\) y\((3,−4+2\sqrt{41})\); asíntotas:\(y=\pm \dfrac{5}{4}(x−3)−4\)

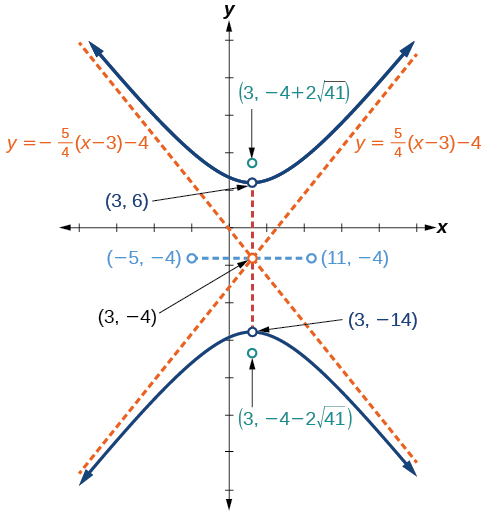
Figura\(\PageIndex{11}\)

Solución de problemas aplicados que involucran hipérbolas

Como comentamos al principio de esta sección, las hipérbolas tienen aplicaciones del mundo real en muchos campos, como la astronomía, la física, la ingeniería y la arquitectura. La eficiencia de diseño de las torres de enfriamiento hiperbólicas es particularmente interesante. Las torres de enfriamiento se utilizan para transferir el calor residual a la atmósfera y a menudo se promocionan por su capacidad para generar energía de manera eficiente. Debido a su forma hiperbólica, estas estructuras son capaces de soportar vientos extremos al tiempo que requieren menos material que cualquier otra forma de su tamaño y resistencia (Figura\(\PageIndex{12}\)). Por ejemplo,\(500\) ¡una torre de pies puede estar hecha de una carcasa de concreto armado solo\(6\) o\(8\) pulgadas de ancho!

Figura\(\PageIndex{12}\): Torres de enfriamiento en la central eléctrica Drax en North Yorkshire, Reino Unido (crédito: Les Haines, Flickr)

Las primeras torres hiperbólicas fueron diseñadas en 1914 y tenían\(35\) metros de altura. Hoy en día, las torres de enfriamiento más altas se encuentran en Francia, con una altura notable de\(170\) metros. En Ejemplo\(\PageIndex{6}\) usaremos la disposición de diseño de una torre de enfriamiento para encontrar una ecuación hiperbólica que modele sus lados.

Ejemplo\(\PageIndex{6}\): Solving Applied Problems Involving Hyperbolas

El diseño de una torre de enfriamiento se muestra en la Figura\(\PageIndex{13}\). La torre mide\(179.6\) metros de altura. El diámetro de la parte superior es de\(72\) metros. En su punto más cercano, los lados de la torre están\(60\) a metros de distancia.

Figura\(\PageIndex{13}\): Diseño de proyecto para una torre de enfriamiento de tiro natural

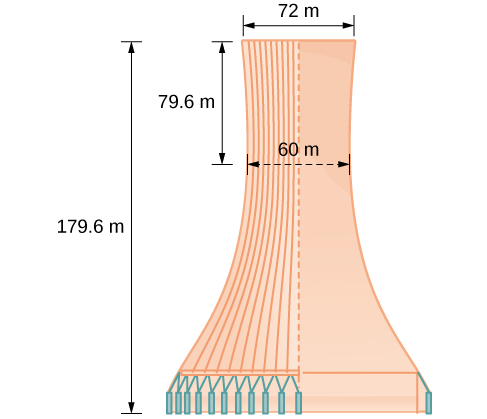
Encuentra la ecuación de la hipérbola que modela los lados de la torre de enfriamiento. Supongamos que el centro de la hipérbola, indicado por la intersección de líneas perpendiculares discontinuas en la figura, es el origen del plano de coordenadas. Redondear los valores finales a cuatro decimales.

Solución

Estamos asumiendo que el centro de la torre está en el origen, por lo que podemos usar la forma estándar de una hipérbola horizontal centrada en el origen:\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), donde las ramas de la hipérbola forman los lados de la torre de enfriamiento. Debemos encontrar los valores de\(a^2\) y\(b^2\) para completar el modelo.

Primero, nos encontramos\(a^2\). Recordemos que la longitud del eje transversal de una hipérbola es\(2a\). Esta longitud se representa por la distancia donde están los lados más cercanos, que se da como\(65.3\) metros. Entonces,\(2a=60\). Por lo tanto,\(a=30\) y\(a^2=900\).

Para resolver\(b^2\), necesitamos sustituir\(x\) y\(y\) en nuestra ecuación usando un punto conocido. Para ello, podemos utilizar las dimensiones de la torre para encontrar algún punto\((x,y)\) que yace sobre la hipérbola. Utilizaremos la esquina superior derecha de la torre para representar ese punto. Dado que el\(y\) eje -divide la torre, nuestro\(x\) -valor puede ser representado por el radio de la parte superior, o\(36\) metros. El valor y se representa por la distancia desde el origen hasta la parte superior, que se da como\(79.6\) metros. Por lo tanto,

\[\begin{align*} \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}&=1\qquad \text{Standard form of horizontal hyperbola.}\\ b^2&=\dfrac{y^2}{\dfrac{x^2}{a^2}-1}\qquad \text{Isolate } b^2\\ &=\dfrac{{(79.6)}^2}{\dfrac{{(36)}^2}{900}-1}\qquad \text{Substitute for } a^2,\: x, \text{ and } y\\ &\approx 14400.3636\qquad \text{Round to four decimal places} \end{align*}\]

Los lados de la torre pueden ser modelados por la ecuación hiperbólica

\(\dfrac{x^2}{900}−\dfrac{y^2}{14400.3636}=1\), o\(\dfrac{x^2}{{30}^2}−\dfrac{y^2}{{120.0015}^2}=1\)

Ejercicio\(\PageIndex{6}\)

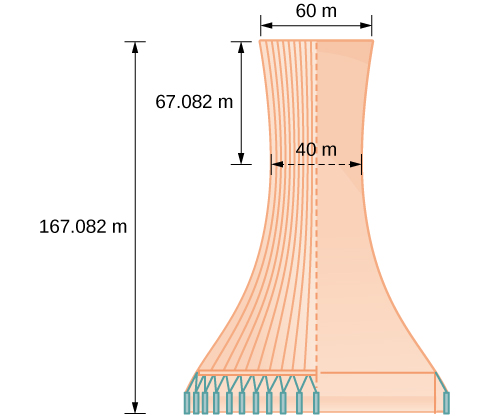
Un diseño para un proyecto de torre de enfriamiento se muestra en la Figura\(\PageIndex{14}\). Encuentra la ecuación de la hipérbola que modela los lados de la torre de enfriamiento. Supongamos que el centro de la hipérbola, indicado por la intersección de líneas perpendiculares discontinuas en la figura, es el origen del plano de coordenadas. Redondear los valores finales a cuatro decimales.

Figura\(\PageIndex{14}\)

Contestar

Los lados de la torre pueden ser modelados por la ecuación hiperbólica. \(\dfrac{x^2}{400}−\dfrac{y^2}{3600}=1\)o\(\dfrac{x^2}{{20}^2}−\dfrac{y^2}{{60}^2}=1\).

Medios

Acceda a estos recursos en línea para obtener instrucción adicional y práctica con hipérbolas.

• Secciones cónicas: La hipérbola Parte 1 de 2
• Secciones cónicas: La hipérbola Parte 2 de 2
• Graficar una hipérbola con centro en origen
• Graficar una hipérbola con centro no en origen

Ecuaciones Clave

Hipérbola, centro de origen, eje transversal sobre eje x	\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\)
Hipérbola, centro de origen, eje transversal sobre eje y	\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\)
Hipérbola, centro en\((h,k)\), eje transversal paralelo al eje x	\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\)
Hipérbola, centro en\((h,k)\), eje transversal paralelo al eje y	\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\)

Conceptos clave

• Una hipérbola es el conjunto de todos los puntos\((x,y)\) en un plano tal que la diferencia de las distancias entre\((x,y)\) y los focos es una constante positiva.
• La forma estándar de una hipérbola se puede utilizar para localizar sus vértices y focos. Ver Ejemplo\(\PageIndex{1}\).
• Cuando se dan las coordenadas de los focos y vértices de una hipérbola, podemos escribir la ecuación de la hipérbola en forma estándar. Ver Ejemplo\(\PageIndex{2}\) y Ejemplo\(\PageIndex{3}\).
• Cuando se le da una ecuación para una hipérbola, podemos identificar sus vértices, co-vértices, focos, asíntotas y longitudes y posiciones de los ejes transversal y conjugado para graficar la hipérbola. Ver Ejemplo\(\PageIndex{4}\) y Ejemplo\(\PageIndex{5}\).
• Las situaciones del mundo real se pueden modelar usando las ecuaciones estándar de hipérbolas. Por ejemplo, dadas las dimensiones de una torre de enfriamiento de tiro natural, podemos encontrar una ecuación hiperbólica que modela sus lados. Ver Ejemplo\(\PageIndex{6}\).