13.2: Secuencias Aritméticas
- Page ID
- 111853
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Encuentra la diferencia común para una secuencia aritmética.
- Escribir términos de una secuencia aritmética.
- Utilice una fórmula recursiva para una secuencia aritmética.
- Utilice una fórmula explícita para una secuencia aritmética.
Las empresas suelen realizar grandes compras, como computadoras y vehículos, para uso comercial. El valor contable de estos suministros disminuye cada año a efectos fiscales. Esta disminución de valor se denomina depreciación. Un método para calcular la depreciación es la depreciación lineal, en la que el valor del activo disminuye por la misma cantidad cada año.
Como ejemplo, consideremos a una mujer que inicia un pequeño negocio de contratación. Ella compra una camioneta nueva para\($25,000\). Después de cinco años, estima que podrá vender la camioneta para\($8,000\). Por lo tanto, la pérdida de valor del camión será\($17,000\), que es\($3,400\) por año por cinco años. El camión valdrá\($21,600\) después del primer año;\($18,200\) después de dos años;\($14,800\) después de tres años;\($11,400\) después de cuatro años; y\($8,000\) al término de cinco años. En esta sección, consideraremos tipos específicos de secuencias que nos permitirán calcular la depreciación, como el valor del camión.
Encontrar diferencias comunes
Se dice que los valores del camión en el ejemplo forman una secuencia aritmética porque cambian en una cantidad constante cada año. Cada término aumenta o disminuye por el mismo valor constante llamado la diferencia común de la secuencia. Para esta secuencia, la diferencia común es\(-3,400\).
La siguiente secuencia es otro ejemplo de una secuencia aritmética. En este caso, la diferencia constante es\(3\). Se puede elegir cualquier término de la secuencia, y agregar\(3\) para encontrar el término posterior.
Una secuencia aritmética es una secuencia que tiene la propiedad de que la diferencia entre dos términos consecutivos cualesquiera es una constante. A esta constante se le llama la diferencia común. Si\(a_1\) es el primer término de una secuencia aritmética y\(d\) es la diferencia común, la secuencia será:
\[\{a_n\}=\{a_1,a_1+d,a_1+2d,a_1+3d,...\}\]
¿Cada secuencia es aritmética? Si es así, encuentra la diferencia común.
- \(\{1,2,4,8,16,...\}\)
- \(\{−3,1,5,9,13,...\}\)
Solución
Restar cada término del término posterior para determinar si existe una diferencia común.
- La secuencia no es aritmética porque no hay diferencia común.
\(2-1={\color{red}1} \qquad 4-2={\color{red}2} \qquad 8-4={\color{red}4} \qquad 16-8={\color{red}8}\)
- La secuencia es aritmética porque hay una diferencia común. La diferencia común es\(4\).
\(1-(-3)={\color{red}4} \qquad 5-1={\color{red}4} \qquad 9-5={\color{red}4} \qquad 13-9={\color{red}4}\)
Análisis
La gráfica de cada una de estas secuencias se muestra en la Figura\(\PageIndex{1}\). Podemos ver en las gráficas que, aunque ambas secuencias muestran crecimiento, (a) no es lineal mientras que (b) es lineal. Las secuencias aritméticas tienen una tasa de cambio constante por lo que sus gráficas siempre serán puntos en una línea.
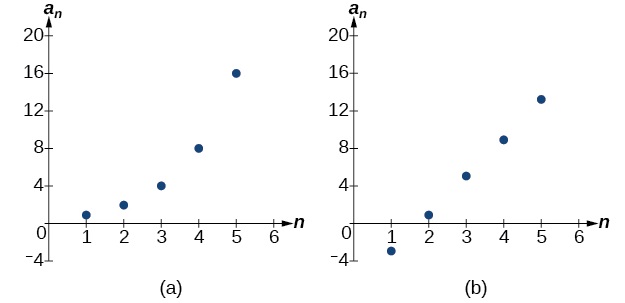
Figura\(\PageIndex{1}\)
Si nos dicen que una secuencia es aritmética, ¿tenemos que restar cada término del siguiente término para encontrar la diferencia común?
No. Si sabemos que la secuencia es aritmética, podemos elegir cualquier término en la secuencia, y restarlo del término posterior para encontrar la diferencia común.
¿La secuencia dada es aritmética? Si es así, encuentra la diferencia común.
\(\{18, 16, 14, 12, 10,…\}\)
- Responder
-
La secuencia es aritmética. La diferencia común es\(–2\).
¿La secuencia dada es aritmética? Si es así, encuentra la diferencia común.
\(\{1, 3, 6, 10, 15,…\}\)
- Responder
-
La secuencia no es aritmética porque\(3−1≠6−3\).
Términos de escritura de secuencias aritméticas
Ahora que podemos reconocer una secuencia aritmética, encontraremos los términos si se nos da el primer término y la diferencia común. Los términos se pueden encontrar comenzando con el primer término y agregando la diferencia común repetidamente. Además, cualquier término también se puede encontrar enchufando los valores de\(n\) y\(d\) en la fórmula a continuación.
\[a_n=a_1+(n−1)d\]
- Agregar la diferencia común al primer término para encontrar el segundo término.
- Agregar la diferencia común al segundo término para encontrar el tercer término.
- Continuar hasta que se identifiquen todos los términos deseados.
- Escribe los términos separados por comas entre paréntesis.
Escribir los primeros cinco términos de la secuencia aritmética con\(a_1=17\) y\(d=−3\).
Solución
Sumar\(−3\) es lo mismo que restar\(3\). A partir del primer término, restar\(3\) de cada término para encontrar el siguiente término.
Los primeros cinco términos son\(\{17,14,11,8,5\}\)
Análisis
Como era de esperar, la gráfica de la secuencia consiste en puntos en una línea como se muestra en la Figura\(\PageIndex{2}\).
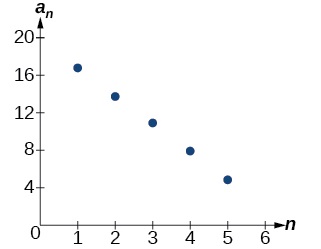
Figura\(\PageIndex{2}\)
Enumere los primeros cinco términos de la secuencia aritmética con\(a_1=1\) y\(d=5\).
- Responder
-
\(\{1, 6, 11, 16, 21\}\)
- Sustituir los valores dados para\(a_1\)\(a_n\),,\(n\) en la fórmula\(a_n=a_1+(n−1)d\) para resolver\(d\).
- Encuentre un término dado sustituyendo los valores apropiados por\(a_1\)\(n\), y\(d\) en la fórmula\(a_n=a_1+(n−1)d\).
Dado\(a_1=8\) y\(a_4=14\), encontrar\(a_5\).
Solución
La secuencia se puede escribir en términos del término inicial\(8\) y la diferencia común\(d\).
\(\{8,8+d,8+2d,8+3d\}\)
Sabemos que el cuarto término es igual\(14\); sabemos que el cuarto término tiene la forma\(a_1+3d=8+3d\).
Podemos encontrar la diferencia común\(d\).
\[\begin{align*} a_n&= a_1+(n-1)d \\ a_4&= a_1+3d \\ a_4&=8+3d\qquad \text{Write the fourth term of the sequence in terms of }a_1 \text{ and } d. \\ 14&=8+3d\qquad \text{Substitute }14 \text{ for } a_4. \\ d&=2\qquad \text{Solve for the common difference.} \end{align*}\]
Encuentra el quinto término sumando la diferencia común al cuarto término.
\(a_5=a_4+2=16\)
Análisis
Observe que la diferencia común se agrega al primer término una vez para encontrar el segundo término, dos veces para encontrar el tercer término, tres veces para encontrar el cuarto término, y así sucesivamente. El décimo término podría encontrarse sumando la diferencia común al primer término nueve veces o usando la ecuación\(a_n=a_1+(n−1)d\).
Dado\(a_3=7\) y\(a_5=17\), encontrar\(a_2\).
- Responder
-
\(a_2=2\)
Uso de fórmulas recursivas para secuencias aritméticas
Algunas secuencias aritméticas se definen en términos del término anterior usando una fórmula recursiva. La fórmula proporciona una regla algebraica para determinar los términos de la secuencia. Una fórmula recursiva nos permite encontrar cualquier término de una secuencia aritmética usando una función del término anterior. Cada término es la suma del término anterior y la diferencia común. Por ejemplo, si la diferencia común es\(5\), entonces cada término es el término anterior más\(5\). Al igual que con cualquier fórmula recursiva, se debe dar el primer término.
\(a_n=a_n−1+d\)
para\(n≥2\)
La fórmula recursiva para una secuencia aritmética con diferencia común\(d\) es:
\[a_n=a_n−1+d\]
para\(n≥2\)
- Restar cualquier término del término posterior para encontrar la diferencia común.
- Anote el término inicial y sustituya la diferencia común en la fórmula recursiva para las secuencias aritméticas.
Escribe una fórmula recursiva para la secuencia aritmética.
\(\{−18, −7, 4, 15, 26, …\}\)
Solución
El primer término se da como\(−18\). La diferencia común se puede encontrar restando el primer término del segundo término.
\(d=−7−(−18)=11\)
Sustituir el término inicial y la diferencia común en la fórmula recursiva para las secuencias aritméticas.
\(a_1=−18\)
\(a_n=a_{n−1}+11\)
para\(n≥2\)
Análisis
Vemos que la diferencia común es la pendiente de la línea formada cuando graficamos los términos de la secuencia, como se muestra en la Figura\(\PageIndex{3}\). El patrón de crecimiento de la secuencia muestra la diferencia constante de 11 unidades.
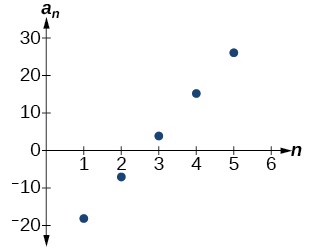
Figura\(\PageIndex{3}\)
¿Hay que restar el primer término del segundo término para encontrar la diferencia común?
No. Podemos restar cualquier término de la secuencia del término posterior. Sin embargo, es más común restar el primer término del segundo término porque suele ser el método más fácil para encontrar la diferencia común.
Escribe una fórmula recursiva para la secuencia aritmética.
\(\{25, 37, 49, 61, …\}\)
- Responder
-
\(\begin{align*}a_1 &= 25 \\ a_n &= a_{n−1}+12 , \text{ for }n≥2 \end{align*}\)
Uso de fórmulas explícitas para secuencias aritméticas
Podemos pensar en una secuencia aritmética como una función en el dominio de los números naturales; es una función lineal porque tiene una tasa de cambio constante. La diferencia común es la tasa constante de cambio, o la pendiente de la función. Podemos construir la función lineal si conocemos la pendiente y la intercepción vertical.
\(a_n=a_1+d(n−1)\)
Para encontrar la\(y\) -intercepción de la función, podemos restar la diferencia común del primer término de la secuencia. Considera la siguiente secuencia.
La diferencia común es\(−50\), por lo que la secuencia representa una función lineal con una pendiente de\(−50\). Para encontrar la\(y\) -intercepción, restamos\(−50\) de\(200\):\(200−(−50)=200+50=250\). También puede encontrar la\(y\) intersección graficando la función y determinando dónde una línea que conecta los puntos se cruzaría con el eje vertical. La gráfica se muestra en la Figura\(\PageIndex{4}\).
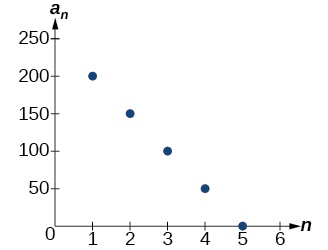
Figura\(\PageIndex{4}\)
Recordemos la forma pendiente-intercepción de una línea es\(y=mx+b\). Cuando se trata de secuencias, utilizamos\(a_n\) en lugar\(y\) y\(n\) en lugar de\(x\). Si conocemos la pendiente y la intersección vertical de la función, podemos sustituirlos por\(m\) y\(b\) en la forma pendiente-intersección de una línea. Sustituyendo\(−50\) por la pendiente y\(250\) por la intercepción vertical, obtenemos la siguiente ecuación:
\(a_n=−50n+250\)
No necesitamos encontrar la intercepción vertical para escribir una fórmula explícita para una secuencia aritmética. Otra fórmula explícita para esta secuencia es\(a_n=200−50(n−1)\), que simplifica a\(a_n=−50n+250\).
Una fórmula explícita para el\(n^{th}\) término de una secuencia aritmética viene dada por
\[a_n=a_1+d(n−1)\]
- Encuentra la diferencia común,\(a_2−a_1\).
- Sustituir la diferencia común y el primer término en\(a_n=a_1+d(n−1)\).
Escribe una fórmula explícita para la secuencia aritmética.
\(\{2, 12, 22, 32, 42, …\}\)
Solución
La diferencia común se puede encontrar restando el primer término del segundo término.
\[\begin{align*} d &= a_2−a_1 \\ &= 12−2 \\ &= 10 \end{align*}\]
La diferencia común es\(10\). Sustituir la diferencia común y el primer término de la secuencia en la fórmula y simplificar.
\[\begin{align*}a_n &= 2+10(n−1) \\ a_n &= 10n−8 \end{align*}\]
Análisis
La gráfica de esta secuencia, representada en la Figura\(\PageIndex{5}\), muestra una pendiente de\(10\) y una intersección vertical de\(−8\).
Figura\(\PageIndex{5}\)
Escriba una fórmula explícita para la siguiente secuencia aritmética.
\(\{50,47,44,41,…\}\)
- Responder
-
\(a_n=53−3n\)
Encontrar el número de términos en una secuencia aritmética finita
Las fórmulas explícitas se pueden utilizar para determinar el número de términos en una secuencia aritmética finita. Necesitamos encontrar la diferencia común, y luego determinar cuántas veces se debe agregar la diferencia común al primer término para obtener el término final de la secuencia.
- Encuentra la diferencia común\(d\).
- Sustituir la diferencia común y el primer término en\(a_n=a_1+d(n–1)\).
- Sustituir el último término por\(a_n\) y resolver para\(n\).
Encuentra el número de términos en la secuencia aritmética finita.
\(\{8, 1, –6, ..., –41\}\)
Solución
La diferencia común se puede encontrar restando el primer término del segundo término.
\(1−8=−7\)
La diferencia común es\(−7\). Sustituir la diferencia común y el término inicial de la secuencia en la fórmula del término n y simplificar.
\[\begin{align*} a_n &= a_1+d(n−1) \\ a_n &= 8+−7(n−1) \\ a_n &= 15−7n \end{align*}\]
Sustituir\(−41\)\(a_n\) y resolver\(n\)
\[\begin{align*} -41&=15-7n\\ 8&=n \end{align*}\]
Hay ocho términos en la secuencia.
Encuentra el número de términos en la secuencia aritmética finita.
\(\{6, 11, 16, ..., 56\}\)
- Responder
-
Hay\(11\) términos en la secuencia.
Resolución de problemas de aplicación con secuencias aritméticas
En muchos problemas de aplicación, a menudo tiene sentido usar un término inicial de\(a_0\) en lugar de\(a_1\). En estos problemas, alteramos ligeramente la fórmula explícita para dar cuenta de la diferencia en términos iniciales. Utilizamos la siguiente fórmula:
\[a_n=a_0+dn\]
Un hijo de cinco años recibe una asignación de\($1\) cada semana. Sus padres le prometen un incremento anual de\($2\) por semana.
- Escribir una fórmula para la asignación semanal del hijo en un año determinado.
- ¿Cuál será la asignación del hijo cuando\(16\) tenga años?
Solución
- La situación puede ser modelada por una secuencia aritmética con un término inicial de\(1\) y una diferencia común de\(2\).
Dejar\(A\) ser el monto de la asignación y\(n\) ser el número de años después de la edad\(5\). Usando la fórmula explícita alterada para una secuencia aritmética obtenemos:
\(A_n=1+2n\)
- Podemos encontrar el número de años desde la edad\(5\) restando.
\(16−5=11\)
Buscamos el subsidio por hijos después de\(11\) años. Sustituir\(11\) en la fórmula para encontrar el subsidio del hijo a la edad\(16\).
\(A_{11}=1+2(11)=23\)
El subsidio por hijo a la edad\(16\) será\($23\) por semana.
Una mujer decide ir a correr un\(10\) minuto todos los días de esta semana y planea aumentar el tiempo de su carrera diaria en\(4\) minutos cada semana. Escribe una fórmula para el momento de su carrera después de\(n\) semanas. ¿Cuánto tiempo va a ser su carrera diaria\(8\) a partir de hoy?
- Responder
-
La fórmula es\(T_n=10+4n\), y le llevará\(42\) minutos.
Acceda a este recurso en línea para obtener instrucción adicional y práctica con secuencias aritméticas.
Ecuaciones Clave
| fórmula recursiva para el enésimo término de una secuencia aritmética | \(a_n=a_{n−1}+d\)\(n≥2\) |
| fórmula explícita para el enésimo término de una secuencia aritmética | \(a_n=a_1+d(n−1)\) |
Key Concepts
- An arithmetic sequence is a sequence where the difference between any two consecutive terms is a constant.
- The constant between two consecutive terms is called the common difference.
- The common difference is the number added to any one term of an arithmetic sequence that generates the subsequent term. See Example \(\PageIndex{1}\).
- The terms of an arithmetic sequence can be found by beginning with the initial term and adding the common difference repeatedly. See Example \(\PageIndex{2}\) and Example \(\PageIndex{3}\).
- A recursive formula for an arithmetic sequence with common difference dd is given by \(a_n=a_{n−1}+d\), \(n≥2\). See Example \(\PageIndex{4}\).
- As with any recursive formula, the initial term of the sequence must be given.
- An explicit formula for an arithmetic sequence with common difference \(d\) is given by \(a_n=a_1+d(n−1)\). See Example \(\PageIndex{5}\).
- An explicit formula can be used to find the number of terms in a sequence. See Example \(\PageIndex{6}\).
- In application problems, we sometimes alter the explicit formula slightly to \(a_n=a_0+dn\). See Example \(\PageIndex{7}\).