12.3: La Parábola
- Page ID
- 112286
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Gráfica parábolas con vértices en el origen.
- Escribir ecuaciones de parábolas en forma estándar.
- Gráfica parábolas con vértices no en el origen.
- Resolver problemas aplicados que involucran parábolas.
¿Sabías que la antorcha olímpica se enciende varios meses antes del inicio de los juegos? El método ceremonial para encender la llama es el mismo que en la antigüedad. La ceremonia se lleva a cabo en el Templo de Hera en Olimpia, Grecia, y tiene sus raíces en la mitología griega, rindiendo homenaje a Prometeo, quien le robó fuego a Zeus para dar a todos los humanos. Una de las once sacerdotisas actuantes coloca la antorcha en el foco de un espejo parabólico (Figura\(\PageIndex{1}\)), que enfoca los rayos de luz del sol para encender la llama.

Los espejos parabólicos (o reflectores) son capaces de capturar energía y enfocarla en un solo punto. Las ventajas de esta propiedad se evidencian en la vasta lista de objetos parabólicos que usamos todos los días: antenas parabólicas, puentes colgantes, telescopios, micrófonos, focos y faros de automóviles, por mencionar algunos. Los reflectores parabólicos también se utilizan en dispositivos de energía alternativa, como cocinas solares y calentadores de agua, porque son económicos de fabricar y necesitan poco mantenimiento. En esta sección exploraremos la parábola y sus usos, incluyendo diseños solares de bajo costo y energéticamente eficientes.
Graficando Parábolas con Vértices en el Origen
Anteriormente, vimos que se forma una elipse cuando un plano corta a través de un cono circular derecho. Si el plano es paralelo al borde del cono, se forma una curva sin límites. Esta curva es una parábola (Figura\(\PageIndex{2}\)).
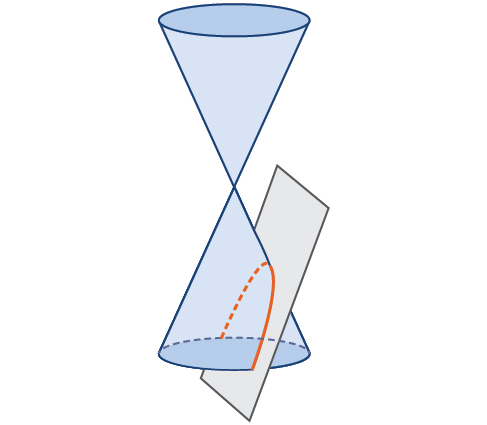
Al igual que la elipse y la hipérbola, la parábola también se puede definir por un conjunto de puntos en el plano de coordenadas. Una parábola es el conjunto de todos los puntos\((x,y)\) en un plano que están a la misma distancia de una línea fija, llamada directriz, y un punto fijo (el foco) no en la directriz.
Anteriormente, aprendimos sobre el vértice y el eje de simetría de una parábola. Ahora ampliamos la discusión para incluir otras características clave de la parábola (Figura\(\PageIndex{3}\)). Observe que el eje de simetría pasa por el foco y vértice y es perpendicular a la directrix. El vértice es el punto medio entre la directrix y el foco. El segmento lineal que pasa por el foco y es paralelo a la directriz se llama recto latus. Los puntos finales del recto latus se encuentran en la curva. Por definición, la distancia d del foco a cualquier punto de\(P\) la parábola es igual a la distancia de\(P\) a la directriz.
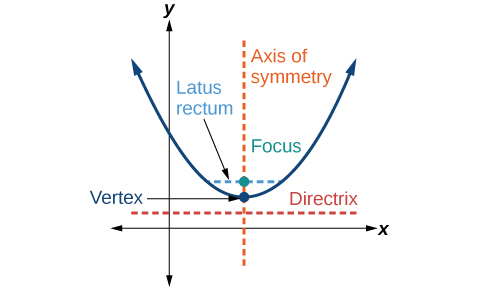
Para trabajar con parábolas en el plano coordenado, consideramos dos casos: aquellos con un vértice en el origen y aquellos con un vértice en un punto distinto al origen. Comenzamos con el primero.
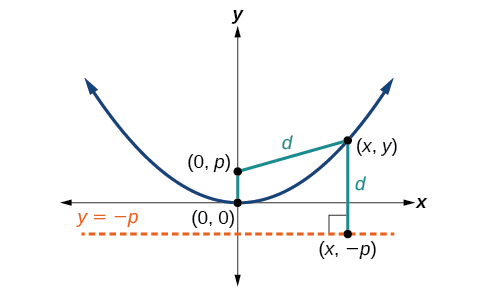
Dejar\((x,y)\) ser un punto en la parábola con vértice\((0,0)\)\((0,p)\), enfoque y directriz\(y=−p\) como se muestra en la Figura\(\PageIndex{4}\). La distancia d de punto\((x,y)\) a punto\((x,−p)\) en la directriz es la diferencia de los valores y:\(d=y+p\). La distancia desde el foco\((0,p)\) hasta el punto también\((x,y)\) es igual\(d\) y se puede expresar usando la fórmula de distancia.
\[ \begin{align*} d &=\sqrt{{(x−0)}^2+{(y−p)}^2} \\[4pt] &=\sqrt{x^2+{(y−p)}^2} \end{align*} \]
Establece las dos expresiones para\(d\) iguales entre sí y resuelve para\(y\) derivar la ecuación de la parábola. Hacemos esto porque la distancia de\((x,y)\) a\((0,p)\) es igual a la distancia de\((x,y)\) a\((x,−p)\).
\[\sqrt{x^2+{(y−p)}^2}=y+p \]
Luego cuadramos ambos lados de la ecuación, expandimos los términos cuadrados y simplificamos combinando términos similares.
\[ \begin{align*} x^2+{(y−p)}^2 &={(y+p)}^2 \\[4pt] x^2+y^2−2py+p^2 &=y^2+2py+p^2 \\[4pt] x^2−2py &=2py \\[4pt] x^2 &=4py \end{align*} \]
Las ecuaciones de parábolas con vértice\((0,0)\) son\(y^2=4px\) cuando el eje x es el eje de simetría y\(x^2=4py\) cuando el eje y es el eje de simetría. Estos formularios estándar se dan a continuación, junto con sus gráficos generales y características clave.
Cuadro\(\PageIndex{1}\) y Figura\(\PageIndex{5}\) resumen las características estándar de las parábolas con un vértice en el origen.
| Eje de simetría | Ecuación | Foco | Directrix | Puntos finales del recto latus |
|---|---|---|---|---|
| eje x | \(y^2=4px\) | \((p, 0)\) | \(x=−p\) | \((p, \pm 2p)\) |
| eje y | \(x^2=4py\) | \((0, p)\) | \(y=−p\) | \((\pm 2p, p)\) |
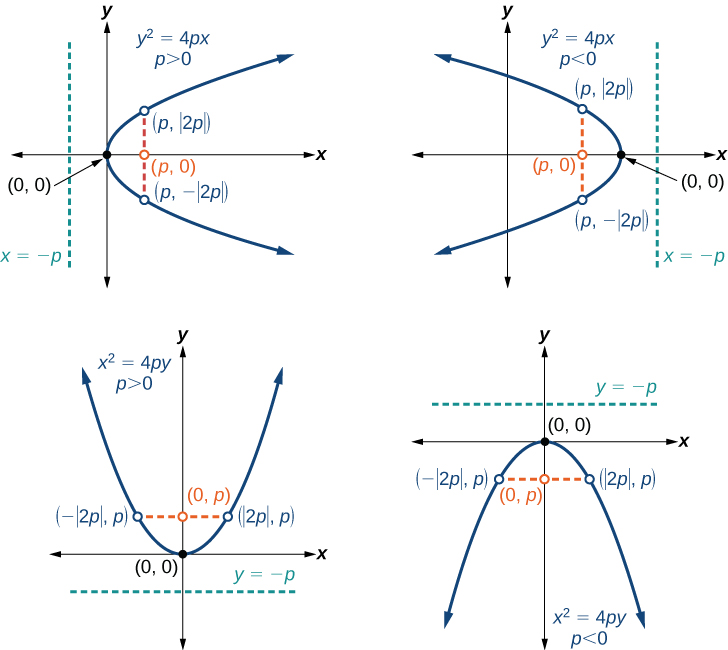
Las características clave de una parábola son su vértice, eje de simetría, foco, directriz y recto latus (Figura\(\PageIndex{5}\)). Cuando se le da una ecuación estándar para una parábola centrada en el origen, podemos identificar fácilmente las características clave para graficar la parábola. Se dice que una línea es tangente a una curva si se cruza con la curva exactamente en un punto. Si esbozamos líneas tangentes a la parábola en los extremos del recto latus, estas líneas se cruzan sobre el eje de simetría, como se muestra en la Figura\(\PageIndex{6}\).
- Determinar cuál de las formas estándar se aplica a la ecuación dada:\(y^2=4px\) o\(x^2=4py\).
- Utilice la forma estándar identificada en el Paso 1 para determinar el eje de simetría, enfoque, ecuación de la directriz y puntos finales del recto latus.
- Si la ecuación está en la forma\(y^2=4px\), entonces
- el eje de simetría es el\(x\) eje -eje,\(y=0\)
- conjunto\(4p\) igual al coeficiente de\(x\) en la ecuación dada para resolver para\(p\). Si\(p>0\), la parábola se abre a la derecha. Si\(p<0\), la parábola se abre a la izquierda.
- utilizar\(p\) para encontrar las coordenadas del foco,\((p,0)\)
- utilizar\(p\) para encontrar la ecuación de la directrix,\(x=−p\)
- utilizar\(p\) para encontrar los puntos finales del recto latus,\((p,\pm 2p)\). Como alternativa, sustituya\(x=p\) en la ecuación original.
- Si la ecuación está en la forma\(x^2=4py\), entonces
- el eje de simetría es el\(y\) eje -eje,\(x=0\)
- conjunto\(4p\) igual al coeficiente de\(y\) en la ecuación dada para resolver para\(p\). Si\(p>0\), la parábola se abre. Si\(p<0\), la parábola se abre hacia abajo.
- utilizar\(p\) para encontrar las coordenadas del foco,\((0,p)\)
- utilizar\(p\) para encontrar la ecuación de la directrix,\(y=−p\)
- utilizar\(p\) para encontrar los puntos finales del recto latus,\((\pm 2p,p)\)
- Si la ecuación está en la forma\(y^2=4px\), entonces
- Trazar el foco, directrix y recto latus, y dibujar una curva suave para formar la parábola.
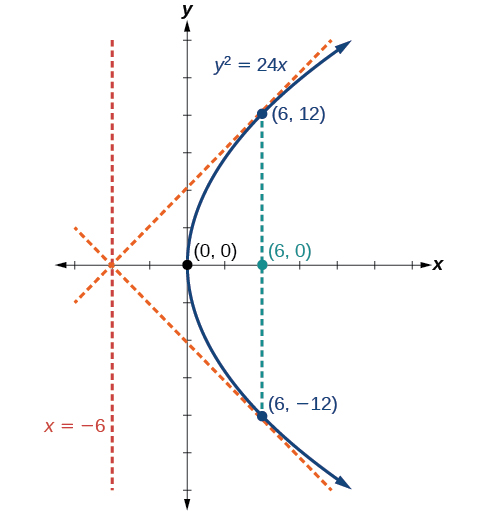
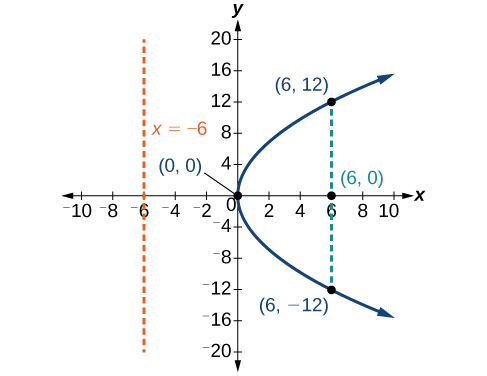
Gráfica\(y^2=24x\). Identificar y etiquetar el foco, directrix y puntos finales del recto latus.
Solución
La forma estándar que se aplica a la ecuación dada es\(y^2=4px\). Así, el eje de simetría es el eje x. De ello se deduce que:
- \(24=4p\), entonces\(p=6\). Ya que\(p>0\), la parábola se abre a la derecha
- las coordenadas del foco son\((p,0)=(6,0)\)
- la ecuación de la directrix es\(x=−p=−6\)
- los puntos finales del recto latus tienen la misma coordenada x en el foco. Para encontrar los puntos finales, sustituya\(x=6\) en la ecuación original:\((6,\pm 12)\)
A continuación trazamos el foco, directriz y recto latus, y dibujamos una curva suave para formar la parábola (Figura\(\PageIndex{7}\)).
Gráfica\(y^2=−16x\). Identificar y etiquetar el foco, directrix y puntos finales del recto latus.
- Contestar
-
- Foco:\((−4,0)\)
- Directrix:\(x=4\)
- Puntos finales del recto latus:\((−4,\pm 8)\)
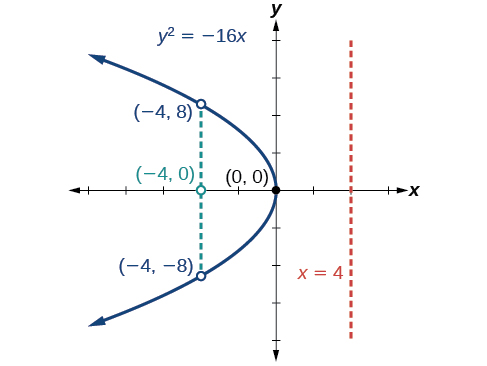
Figura\(\PageIndex{8}\)
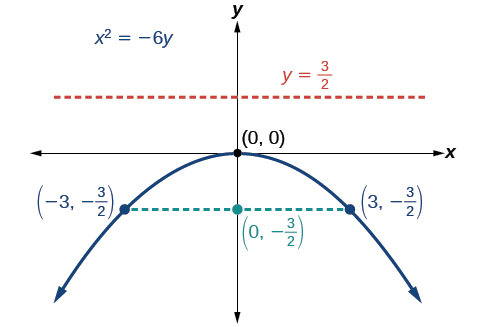
Gráfica\(x^2=−6y\). Identificar y etiquetar el foco, directrix y puntos finales del recto latus.
Solución
La forma estándar que se aplica a la ecuación dada es\(x^2=4py\). Así, el eje de simetría es el\(y\) eje -eje. De ello se deduce que:
- \(−6=4p\), entonces\(p=−\dfrac{3}{2}\). Ya que\(p<0\), la parábola se abre hacia abajo.
- las coordenadas del foco son\((0,p)=(0,−\dfrac{3}{2})\)
- la ecuación de la directrix es\(y=−p=\dfrac{3}{2}\)
- los puntos finales del recto latus se pueden encontrar sustituyendo\(y=\dfrac{3}{2}\) en la ecuación original,\((\pm 3,−\dfrac{3}{2})\)
A continuación trazamos el foco, directriz y recto latus, y dibujamos una curva suave para formar la parábola.
Gráfica\(x^2=8y\). Identificar y etiquetar el foco, directrix y puntos finales del recto latus.
- Contestar
-
- Foco:\((0,2)\)
- Directrix:\(y=−2\)
- Puntos finales del recto latus:\((\pm 4,2)\).
Figura\(\PageIndex{10}\)
Escribir ecuaciones de parábolas en forma estándar
En los ejemplos anteriores, se utilizó la ecuación de forma estándar de una parábola para calcular las ubicaciones de sus características clave. También podemos usar los cálculos a la inversa para escribir una ecuación para una parábola cuando se dan sus características clave.
- Determinar si el eje de simetría es el eje\(x\) - o\(y\) -eje.
- Si las coordenadas dadas del foco tienen la forma\((p,0)\), entonces el eje de simetría es el\(x\) eje -eje. Utilice el formulario estándar\(y^2=4px\).
- Si las coordenadas dadas del foco tienen la forma\((0,p)\), entonces el eje de simetría es el\(y\) eje -eje. Utilice el formulario estándar\(x^2=4py\).
- Multiplicar\(4p\).
- Sustituir el valor del Paso 2 en la ecuación determinada en el Paso 1.
¿Cuál es la ecuación para la parábola con enfoque\((−\dfrac{1}{2},0)\) y directrix\(x=\dfrac{1}{2}\)?
Solución
El foco tiene la forma\((p,0)\), por lo que la ecuación tendrá la forma\(y^2=4px\).
- Multiplicando\(4p\), tenemos\(4p=4(−\dfrac{1}{2})=−2\).
- Sustituyendo por\(4p\), tenemos\(y^2=4px=−2x\). =
Por lo tanto, la ecuación para la parábola es\(y^2=−2x\).
¿Cuál es la ecuación para la parábola con enfoque\(\left(0,\dfrac{7}{2}\right)\) y directrix\(y=−\dfrac{7}{2}\)?
- Contestar
-
\(x^2=14y\).
Graficando Parábolas con Vértices que no están en el Origen
Al igual que otras gráficas con las que hemos trabajado, se puede traducir la gráfica de una parábola. Si una parábola se traduce\(h\) unidades horizontalmente y\(k\) unidades verticalmente, el vértice será\((h,k)\). Esta traducción da como resultado la forma estándar de la ecuación que vimos previamente con\(x\) reemplazada por\((x−h)\) y\(y\) reemplazada por\((y−k)\).
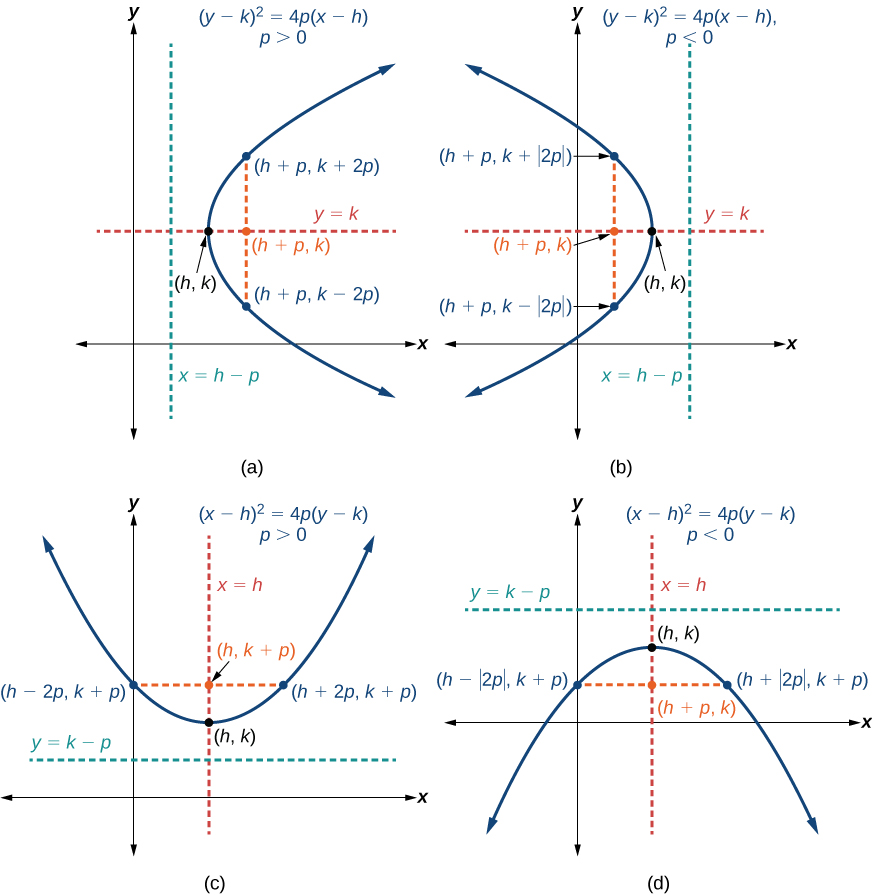
Para graficar parábolas con un vértice\((h,k)\) distinto al origen, utilizamos la forma estándar\({(y−k)}^2=4p(x−h)\) para las parábolas que tienen un eje de simetría paralelo al\(x\) eje -y\({(x−h)}^2=4p(y−k)\) para las parábolas que tienen un eje de simetría paralelo al\(y\) eje -eje. Estos formularios estándar se dan a continuación, junto con sus gráficos generales y características clave.
Tabla\(\PageIndex{2}\) y Figura\(\PageIndex{11}\) resumen las características estándar de las parábolas con un vértice en un punto\((h,k)\).
| Eje de simetría | Ecuación | Foco | Directrix | Puntos finales del recto latus |
|---|---|---|---|---|
| \(y=k\) | \({(y−k)}^2=4p(x−h)\) | \((h+p, k)\) | \(x=h−p\) | \((h+p, k\pm 2p)\) |
| \(x=h\) | \({(x−h)}^2=4p(y−k)\) | \((h, k+p)\) | \(y=k−p\) | \((h\pm 2p, k+p)\) |
- Determinar cuál de las formas estándar se aplica a la ecuación dada:\({(y−k)}^2=4p(x−h)\) o\({(x−h)}^2=4p(y−k)\).
- Utilice la forma estándar identificada en el Paso 1 para determinar el vértice, el eje de simetría, el enfoque, la ecuación de la directriz y los puntos finales del recto latus.
- Si la ecuación está en la forma\({(y−k)}^2=4p(x−h)\), entonces:
- utilizar la ecuación dada para identificar\(h\) y\(k\) para el vértice,\((h,k)\)
- utilizar el valor de\(k\) para determinar el eje de simetría,\(y=k\)
- conjunto\(4p\) igual al coeficiente de\((x−h)\) en la ecuación dada para resolver para\(p\). Si\(p>0\), la parábola se abre a la derecha. Si\(p<0\), la parábola se abre a la izquierda.
- utilizar\(h\),\(k\), y\(p\) para encontrar las coordenadas del foco,\((h+p, k)\)
- utilizar\(h\) andp p para encontrar la ecuación de la directrix,\(x=h−p\)
- usar\(h\),\(k\), y\(p\) para encontrar los puntos finales del recto latus,\((h+p,k\pm 2p)\)
- Si la ecuación está en la forma\({(x−h)}^2=4p(y−k)\), entonces:
- utilizar la ecuación dada para identificar\(h\) y\(k\) para el vértice,\((h,k)\)
- utilizar el valor de\(h\) para determinar el eje de simetría,\(x=h\)
- conjunto\(4p\) igual al coeficiente de\((y−k)\) en la ecuación dada para resolver para\(p\). Si\(p>0\), la parábola se abre. Si\(p<0\), la parábola se abre hacia abajo.
- utilizar\(h\),\(k\), y\(p\) para encontrar las coordenadas del foco,\((h, k+p)\)
- utilizar\(k\) y\(p\) encontrar la ecuación de la directrix,\(y=k−p\)
- usar\(h\),\(k\), y\(p\) para encontrar los puntos finales del recto latus,\((h\pm 2p, k+p)\)
- Si la ecuación está en la forma\({(y−k)}^2=4p(x−h)\), entonces:
- Trazar el vértice, el eje de simetría, el foco, la directriz y el recto latus, y dibuja una curva suave para formar la parábola.
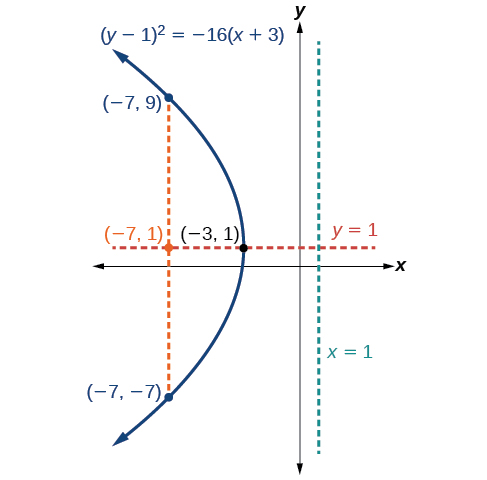
Gráfica\({(y−1)}^2=−16(x+3)\). Identificar y etiquetar el vértice, eje de simetría, foco, directrix y puntos finales del recto latus.
Solución
La forma estándar que se aplica a la ecuación dada es\({(y−k)}^2=4p(x−h)\). Así, el eje de simetría es paralelo al\(x\) eje -eje. De ello se deduce que:
- el vértice es\((h,k)=(−3,1)\)
- el eje de simetría es\(y=k=1\)
- \(−16=4p\), entonces\(p=−4\). Ya que\(p<0\), la parábola se abre a la izquierda.
- las coordenadas del foco son\((h+p,k)=(−3+(−4),1)=(−7,1)\)
- la ecuación de la directrix es\(x=h−p=−3−(−4)=1\)
- los puntos finales del recto latus son\((h+p,k\pm 2p)=(−3+(−4),1\pm 2(−4))\), o\((−7,−7)\) y\((−7,9)\)
A continuación trazamos el vértice, eje de simetría, foco, directriz y recto latus, y dibujamos una curva suave para formar la parábola (Figura\(\PageIndex{10}\)).
Gráfica\({(y+1)}^2=4(x−8)\). Identificar y etiquetar el vértice, el eje de simetría, el foco, la directriz y los puntos finales del recto latus.
- Contestar
-
- Vértice:\((8,−1)\)
- Eje de simetría:\(y=−1\)
- Foco:\((9,−1)\)
- Directrix:\(x=7\)
- Puntos finales del recto latus:\((9,−3)\) y\((9,1)\).
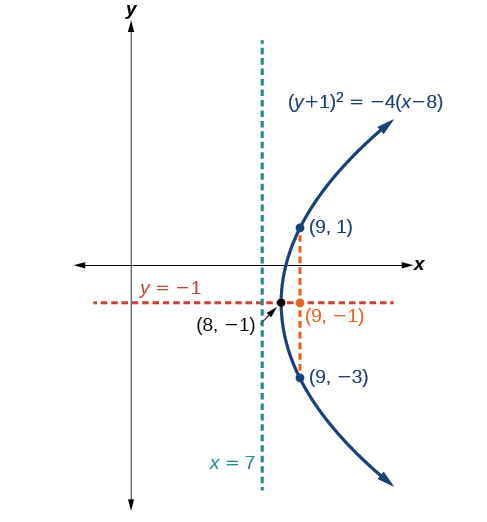
Figura\(\PageIndex{13}\)
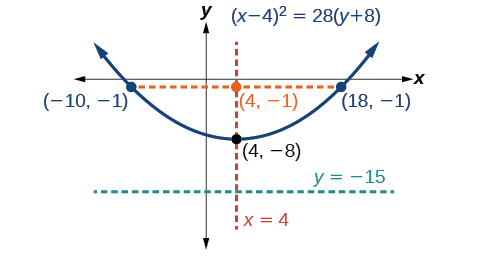
Gráfica\(x^2−8x−28y−208=0\). Identificar y etiquetar el vértice, el eje de simetría, el foco, la directriz y los puntos finales del recto latus.
Solución
Comience por escribir la ecuación de la parábola en forma estándar. La forma estándar que se aplica a la ecuación dada es\({(x−h)}^2=4p(y−k)\). Así, el eje de simetría es paralelo al\(y\) eje -eje. Para expresar la ecuación de la parábola en esta forma, comenzamos aislando los términos que contienen\(x\) la variable para completar el cuadrado.
\[ \begin{align*} x^2−8x−28y−208&=0 \\[4pt] x^2−8x &=28y+208 \\[4pt] x^2−8x+16 &=28y+208+16 \\[4pt] (x−4)^2 &=28y+224 \\[4pt] (x−4)^2 &=28(y+8) \\[4pt] (x−4)^2&= 4⋅7⋅(y+8) \end{align*}\]
De ello se deduce que:
- el vértice es\((h,k)=(4,−8)\)
- el eje de simetría es\(x=h=4\)
- ya que\(p=7\),\(p>0\) y así se abre la parábola
- las coordenadas del foco son\((h,k+p)=(4,−8+7)=(4,−1)\)
- la ecuación de la directrix es\(y=k−p=−8−7=−15\)
- los puntos finales del recto latus son\((h\pm 2p,k+p)=(4\pm 2(7),−8+7)\), o\((−10,−1)\) y\((18,−1)\)
A continuación trazamos el vértice, eje de simetría, foco, directriz y recto latus, y dibujamos una curva suave para formar la parábola (Figura\(\PageIndex{14}\)).
Gráfica\({(x+2)}^2=−20(y−3)\). Identificar y etiquetar el vértice, el eje de simetría, el foco, la directriz y los puntos finales del recto latus.
- Contestar
-
- Vértice:\((−2,3)\)
- Eje de simetría:\(x=−2\)
- Foco:\((−2,−2)\)
- Directrix:\(y=8\)
- Puntos finales del recto latus:\((−12,−2)\) y\((8,−2)\).
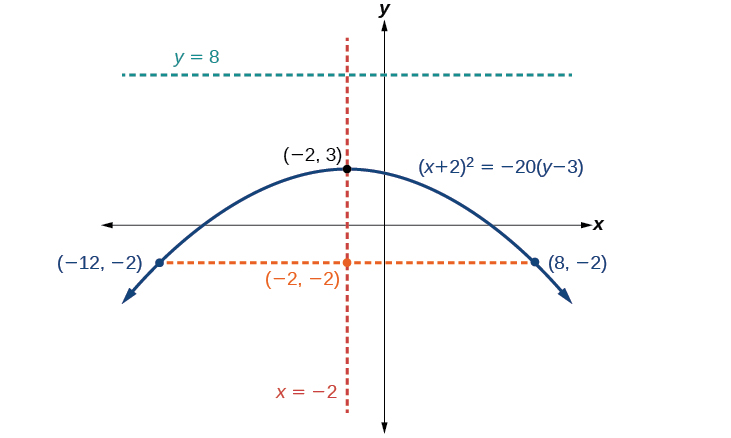
Figura\(\PageIndex{15}\)
Solución de problemas aplicados que involucran parábolas
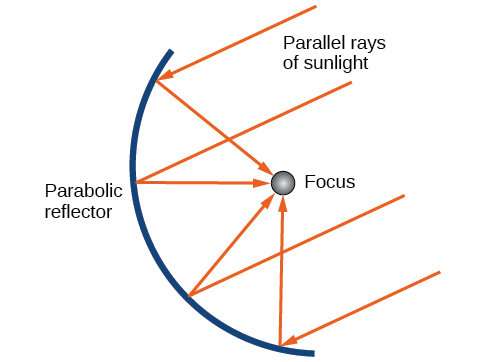
Como mencionamos al inicio de la sección, las parábolas se utilizan para diseñar muchos objetos que usamos todos los días, como telescopios, puentes colgantes, micrófonos y equipos de radar. Los espejos parabólicos, como el que se utiliza para encender la antorcha olímpica, tienen una propiedad reflectante muy singular. Cuando los rayos de luz paralelos al eje de simetría de la parábola se dirigen hacia cualquier superficie del espejo, la luz se refleja directamente al foco (Figura\(\PageIndex{16}\)). Es por ello que la antorcha olímpica se enciende cuando se sostiene en el foco del espejo parabólico.
Los espejos parabólicos tienen la capacidad de enfocar la energía del sol a un solo punto, elevando la temperatura cientos de grados en cuestión de segundos. Por lo tanto, los espejos parabólicos se presentan en muchos productos solares de bajo costo y energéticamente eficientes, como cocinas solares, calentadores solares e incluso arrancadores de fuego del tamaño de viaje.
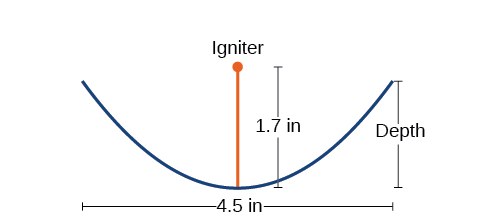
Una sección transversal de un diseño para un arrancador de fuego solar del tamaño de viaje se muestra en la Figura\(\PageIndex{17}\). Los rayos del sol se reflejan en el espejo parabólico hacia un objeto unido al encendedor. Debido a que el encendedor se encuentra en el foco de la parábola, los rayos reflejados hacen que el objeto se queme en tan solo segundos.
- Encuentra la ecuación de la parábola que modela el arrancador de fuego. Supongamos que el vértice del espejo parabólico es el origen del plano coordenado.
- Usa la ecuación que se encuentra en la parte (a) para encontrar la profundidad del iniciador de fuego.
Solución
- El vértice del plato es el origen del plano coordenado, por lo que la parábola tomará la forma estándar\(x^2=4py\), donde\(p>0\). El encendedor, que es el foco, está a\(1.7\) centímetros por encima del vértice del platillo. Así tenemos\(p=1.7\).
\[\begin{align*} x^2&=4py\qquad \text{Standard form of upward-facing parabola with vertex } (0,0)\\ x^2&=4(1.7)y\qquad \text{Substitute } 1.7 \text{ for } p\\ x^2&=6.8y\qquad \text{Multiply.} \end{align*}\]
- El platillo se extiende\(\dfrac{4.5}{2}=2.25\) pulgadas a cada lado del origen. Podemos sustituir\(x\) en\(2.25\) la ecuación de la parte (a) para encontrar la profundidad del platillo.
\[\begin{align*} x^2&=6.8y\qquad \text{ Equation found in part } (a)\\ {(2.25)}^2&=6.8y\qquad \text{Substitute } 2.25 \text{ for } x\\ y&\approx 0.74\qquad \text{Solve for } y \end{align*}\]
El platillo tiene unos\(0.74\) centímetros de profundidad.
Las cocinas solares del tamaño de un balcón han sido diseñadas para familias que viven en la India. La parte superior de un plato tiene un diámetro de\(1600\) mm. Los rayos del sol se reflejan en el espejo parabólico hacia la “cocina”, que se coloca a\(320\) mm de la base.
- Encuentre una ecuación que modele una sección transversal de la cocina solar. Supongamos que el vértice del espejo parabólico es el origen del plano coordenado, y que la parábola se abre a la derecha (es decir, tiene el eje x como eje de simetría).
- Usa la ecuación que se encuentra en la parte (a) para encontrar la profundidad de la olla.
- Contestar a
-
\(y^2=1280x\)
- Respuesta b
-
La profundidad de la olla es\(500\) mm
Ecuaciones Clave
| Parábola, vértice en origen, eje de simetría sobre eje x | \(y^2=4px\) |
| Parábola, vértice en origen, eje de simetría sobre eje y | \(x^2=4py\) |
| Parábola, vértice en\((h,k)\), eje de simetría en el eje x | \({(y−k)}^2=4p(x−h)\) |
| Parábola, vértice en\((h,k)\), eje de simetría en el eje y | \({(x−h)}^2=4p(y−k)\) |
Conceptos clave
- Una parábola es el conjunto de todos los puntos\((x,y)\) en un plano que están a la misma distancia de una línea fija, llamada directriz, y un punto fijo (el foco) no en la directriz.
- La forma estándar de una parábola con vértice\((0,0)\) y el eje x como eje de simetría se puede utilizar para graficar la parábola. Si\(p>0\), la parábola se abre a la derecha. Si\(p<0\), la parábola se abre a la izquierda. Ver Ejemplo\(\PageIndex{1}\).
- La forma estándar de una parábola con vértice\((0,0)\) y el eje y como eje de simetría se puede utilizar para graficar la parábola. Si\(p>0\), la parábola se abre. Si\(p<0\), la parábola se abre hacia abajo. Ver Ejemplo\(\PageIndex{2}\).
- Cuando se le da el foco y directrix de una parábola, podemos escribir su ecuación en forma estándar. Ver Ejemplo\(\PageIndex{3}\).
- La forma estándar de una parábola con vértice\((h,k)\) y eje de simetría paralelos al\(x\) eje -se puede utilizar para graficar la parábola. Si\(p>0\), la parábola se abre a la derecha. Si\(p<0\), la parábola se abre a la izquierda. Ver Ejemplo\(\PageIndex{4}\).
- La forma estándar de una parábola con vértice\((h,k)\) y eje de simetría paralelos al\(y\) eje -se puede utilizar para graficar la parábola. Si\(p>0\), la parábola se abre. Si\(p<0\), la parábola se abre hacia abajo. Ver Ejemplo\(\PageIndex{5}\).
- Las situaciones del mundo real se pueden modelar usando las ecuaciones estándar de las parábolas. Por ejemplo, dado el diámetro y foco de una sección transversal de un reflector parabólico, podemos encontrar una ecuación que modele sus lados. Ver Ejemplo\(\PageIndex{6}\).


