3.2: Funciones y notación de funciones
- Page ID
- 116957
Objetivos de aprendizaje
- Determinar si una relación representa una función.
- Encuentra el valor de una función.
- Determine si una función es uno a uno.
- Utilice la prueba de línea vertical para identificar funciones.
- Grafique las funciones enumeradas en la biblioteca de funciones.
Un avión cambia de altitud a medida que aumenta su distancia desde el punto de partida de un vuelo. El peso de un niño en crecimiento aumenta con el tiempo. En cada caso, una cantidad depende de otra. Existe una relación entre las dos cantidades que podemos describir, analizar y usar para hacer predicciones. En esta sección, analizaremos dichas relaciones.
Determinar si una relación representa una función
Una relación es un conjunto de pares ordenados. El conjunto de los primeros componentes de cada par ordenado se llama dominio y el conjunto de los segundos componentes de cada par ordenado se llama rango. Considera el siguiente conjunto de pares ordenados. Los primeros números de cada par son los primeros cinco números naturales. El segundo número de cada par es el doble que el del primero.
\[\{(1, 2), (2, 4), (3, 6), (4, 8), (5, 10)\}\tag{1.1.1}\]
El dominio es\(\{1, 2, 3, 4, 5\}\). El rango es\(\{2, 4, 6, 8, 10\}\).
Tenga en cuenta que cada valor en el dominio también se conoce como un valor de entrada, o variable independiente, y a menudo se etiqueta con la letra minúscula\(x\). Cada valor en el rango también se conoce como un valor de salida, o variable dependiente, y a menudo se etiqueta letra minúscula\(y\).
Una función\(f\) es una relación que asigna un solo valor en el rango a cada valor en el dominio. En otras palabras, no se repiten\(x\) valores -. Para nuestro ejemplo que relaciona los cinco primeros números naturales con números duplican sus valores, esta relación es una función porque cada elemento en el dominio, {1, 2, 3, 4, 5}, está emparejado con exactamente un elemento en el rango,\(\{2, 4, 6, 8, 10\}\).
Ahora consideremos el conjunto de pares ordenados que relaciona los términos “par” e “impar” con los primeros cinco números naturales. Aparecería como
\[\mathrm{\{(odd, 1), (even, 2), (odd, 3), (even, 4), (odd, 5)\}} \tag{1.1.2}\]
Observe que cada elemento en el dominio, {par, impar} no está emparejado con exactamente un elemento en el rango,\(\{1, 2, 3, 4, 5\}\). Por ejemplo, el término “impar” corresponde a tres valores del rango,\(\{1, 3, 5\},\) y el término “par” corresponde a dos valores del rango,\(\{2, 4\}\). Esto viola la definición de una función, por lo que esta relación no es una función.
La figura\(\PageIndex{1}\) compara relaciones que son funciones y no funciones.
![[Tres relaciones que demuestran lo que constituye una función.]](https://math.libretexts.org/@api/deki/files/861/CNX_Precalc_Figure_01_01_001.jpg)
Función
Una función es una relación en la que cada posible valor de entrada conduce a exactamente un valor de salida. Decimos “la salida es una función de la entrada”.
Los valores de entrada conforman el dominio, y los valores de salida conforman el rango.
Cómo: Dada una relación entre dos cantidades, determinar si la relación es una función
- Identificar los valores de entrada.
- Identificar los valores de salida.
- Si cada valor de entrada conduce a un solo valor de salida, clasifique la relación como una función. Si algún valor de entrada conduce a dos o más salidas, no clasifique la relación como una función.
Ejemplo\(\PageIndex{1}\): Determining If Menu Price Lists Are Functions
El menú de la cafetería, que se muestra en la Figura\(\PageIndex{2}\) consiste en artículos y sus precios.
- ¿El precio es una función del artículo?
- ¿El artículo es una función del precio?
Solución
- Comencemos considerando la entrada como los elementos del menú. Los valores de salida son entonces los precios. Ver Figura\(\PageIndex{3}\).
![[Un menú de precios de donas de una cafetería donde una dona simple cuesta $1.49 y una donut de gelatina y donut de chocolate son $1.99.]](https://math.libretexts.org/@api/deki/files/865/CNX_Precalc_Figure_01_01_027.v2.jpg)
Cada elemento del menú tiene un solo precio, por lo que el precio es una función del artículo.
- Dos elementos del menú tienen el mismo precio. Si consideramos que los precios son los valores de entrada y los ítems como la salida, entonces el mismo valor de entrada podría tener más de una salida asociada a él. Ver Figura\(\PageIndex{4}\).
![[Asociación de los precios a las donas.]](https://math.libretexts.org/@api/deki/files/866/CNX_Precalc_Figure_01_01_028.jpg)
Por lo tanto, el artículo no es una función de precio.
Ejemplo\(\PageIndex{2}\): Determining If Class Grade Rules Are Functions
En una clase particular de matemáticas, la calificación porcentual general corresponde a un promedio de calificaciones. ¿El promedio de calificaciones es una función de la calificación porcentual? ¿La calificación porcentual es una función del promedio de calificaciones? \(\PageIndex{1}\)La tabla muestra una posible regla para asignar puntos de calificación.
| Grado porcentual | 0—56 | 57—61 | 62—66 | 67—71 | 72—77 | 78—86 | 87—91 | 92—100 |
| Promedio del punto de calificación | 0.0 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Solución
Para cualquier grado porcentual obtenido, hay un promedio de calificaciones asociado, por lo que el promedio de calificaciones es una función de la calificación porcentual. En otras palabras, si ingresamos la calificación porcentual, el resultado es un promedio de calificaciones específico.
En el sistema de calificaciones dado, existe un rango de calificaciones porcentuales que corresponden al mismo promedio de calificaciones. Por ejemplo, los estudiantes que reciben un promedio de calificaciones de 3.0 podrían tener una variedad de calificaciones porcentuales que van desde 78 hasta 86. Por lo tanto, el porcentaje de calificación no es una función del promedio de calificaciones.
Ejercicio\(\PageIndex{2}\)
En la tabla se\(\PageIndex{2}\) enumeran los cinco mejores beisbolistas de todos los tiempos en orden de rango.
| Jugador | Rango |
|---|---|
| Babe Ruth | 1 |
| Willie Mays | 2 |
| Ty Cobb | 3 |
| Walter Johnson | 4 |
| Hank Aarón | 5 |
- ¿El rango es una función del nombre del jugador?
- ¿El nombre del jugador es una función del rango?
- Contestar a
-
Sí
- Respuesta b
-
Sí. (Nota: Si dos jugadores hubieran estado empatados por, digamos, el 4to lugar, entonces el nombre no habría sido una función de rango.)
Uso de la notación de funciones
Una vez que determinamos que una relación es una función, necesitamos mostrar y definir las relaciones funcionales para que podamos entenderlas y usarlas, y a veces también para que podamos programarlas en computadoras. Existen diversas formas de representar funciones. Una notación de función estándar es una representación que facilita el trabajo con funciones.
Para representar “la altura es una función de la edad”, comenzamos por identificar las variables descriptivas\(h\) para la altura y\(a\) para la edad. Las letras\(f\),\(g\), y\(h\) a menudo se utilizan para representar funciones tal como usamos\(x\),\(y\), y\(z\) para representar números y\(A\),\(B\), y\(C\) para representar conjuntos.
\[\begin{array}{ll} h \text{ is } f \text{ of }a \;\;\;\;\;\; & \text{We name the function }f \text{; height is a function of age.} \\ h=f(a) & \text{We use parentheses to indicate the function input.} \\ f(a) & \text{We name the function }f \text{ ; the expression is read as “ }f \text{ of }a \text{.”}\end{array}\]
Recuerda, podemos usar cualquier letra para nombrar la función; la notación nos\(h(a)\) muestra que\(h\) depende de\(a\). El valor\(a\) debe ser puesto en la función\(h\) para obtener un resultado. Los paréntesis indican que la edad se introduce en la función; no indican multiplicación.
También podemos dar una expresión algebraica como entrada a una función. Por ejemplo\(f(a+b)\) significa “primero agregar\(a\) y\(b\), y el resultado es la entrada para la función”\(f\). Las operaciones deben realizarse en este orden para obtener el resultado correcto.
Notación de funciones
La notación\(y=f(x)\) define una función llamada\(f\). Esto se lee como “\(y\)es una función de”\(x\). La letra\(x\) representa el valor de entrada, o variable independiente. La letra\(y\), o\(f(x)\), representa el valor de salida, o variable dependiente.
Ejemplo\(\PageIndex{3}\): Using Function Notation for Days in a Month
Utilice la notación de función para representar una función cuya entrada es el nombre de un mes y la salida es el número de días en ese mes.
Solución
Uso de la notación de funciones para días en un mes
Utilice la notación de función para representar una función cuya entrada es el nombre de un mes y la salida es el número de días en ese mes.
El número de días en un mes es una función del nombre del mes, así que si nombramos la función\(f\), escribimos\(\text{days}=f(\text{month})\) o\(d=f(m)\). El nombre del mes es la entrada a una “regla” que asocia un número específico (la salida) con cada entrada.
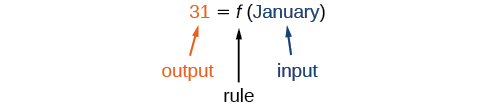
Por ejemplo,\(f(\text{March})=31\), porque marzo tiene 31 días. La notación nos\(d=f(m)\) recuerda que el número de días,\(d\) (la salida), depende del nombre del mes,\(m\) (la entrada).
Análisis
Tenga en cuenta que las entradas a una función no tienen que ser números; las entradas de función pueden ser nombres de personas, etiquetas de objetos geométricos o cualquier otro elemento que determine algún tipo de salida. Sin embargo, la mayoría de las funciones con las que trabajaremos en este libro tendrán números como entradas y salidas.
Ejemplo\(\PageIndex{3B}\): Interpreting Function Notation
Una función\(N=f(y)\) da el número de policías,\(N\), en una localidad en año\(y\). ¿Qué\(f(2005)=300\) representa?
Solución
Cuando leemos\(f(2005)=300\), vemos que el año insumo es 2005. El valor para la salida, el número de policías\((N)\), es de 300. Recuerda,\(N=f(y)\). El comunicado nos\(f(2005)=300\) dice que en el año 2005 había 300 policías en la localidad.
Ejercicio\(\PageIndex{3}\)
Utilice la notación de funciones para expresar el peso de un cerdo en libras en función de su edad en días\(d\).
- Contestar
-
\(w=f(d)\)
Q&A
En lugar de una notación como\(y=f(x)\), ¿podríamos usar el mismo símbolo para la salida que para la función, tal como\(y=y(x)\), que significa “\(y\)es una función de\(x\)?”
Sí, esto se suele hacer, especialmente en asignaturas aplicadas que utilizan matemáticas superiores, como la física y la ingeniería. Sin embargo, al explorar la propia matemática nos gusta mantener una distinción entre una función como\(f\), que es una regla o procedimiento, y la salida y que obtenemos al aplicar\(f\) a una entrada particular\(x\). Es por ello que solemos usar notación como\(y=f(x),P=W(d)\), y así sucesivamente.
Representación de funciones mediante tablas
Un método común para representar funciones es en forma de tabla. Las filas o columnas de la tabla muestran los valores de entrada y salida correspondientes. En algunos casos, estos valores representan todo lo que sabemos sobre la relación; otras veces, la tabla proporciona algunos ejemplos selectos de una relación más completa.
Tabla\(\PageIndex{3}\) enumera el número de entrada de cada mes (\(\text{January}=1\)\(\text{February}=2\),, y así sucesivamente) y el valor de salida del número de días en ese mes. Esta información representa todo lo que sabemos sobre los meses y días de un año determinado (que no es un año bisiesto). Tenga en cuenta que, en esta tabla, definimos una función days-in-a-month\(f\) donde\(D=f(m)\) identifica meses por un entero en lugar de por nombre.
| Número de mes,\(m\) (entrada) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Días en el mes,\(D\) (salida) | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
Tabla\(\PageIndex{4}\) define una función\(Q=g(n)\) Recordar, esta notación nos dice que\(g\) es el nombre de la función que toma la entrada\(n\) y da la salida\(Q\).
| \(n\) | 1 | 2 | 3 | 4 | 5 |
| \(Q\) | 8 | 6 | 7 | 6 | 8 |
La tabla\(\PageIndex{5}\) muestra la edad de los niños en años y sus alturas correspondientes. Esta tabla muestra solo algunos de los datos disponibles para las alturas y edades de los niños. Podemos ver de inmediato que esta tabla no representa una función porque el mismo valor de entrada, 5 años, tiene dos valores de salida diferentes, 40 pulg. y 42 pulg.
| Edad en años,\(a\) (entrada) | 5 | 5 | 6 | 7 | 8 | 9 | 10 |
| Altura en pulgadas,\(h\) (salida) | 40 | 42 | 44 | 47 | 50 | 52 | 54 |
Cómo: Dada una tabla de valores de entrada y salida, determinar si la tabla representa una función
- Identificar los valores de entrada y salida.
- Verifique si cada valor de entrada está emparejado con un solo valor de salida. Si es así, la tabla representa una función.
Ejemplo\(\PageIndex{5}\): Identifying Tables that Represent Functions
¿Qué tabla, Tabla\(\PageIndex{6}\)\(\PageIndex{7}\), Tabla o Tabla\(\PageIndex{8}\) representa una función (si la hay)?
| Entrada | Salida |
|---|---|
| 2 | 1 |
| 5 | 3 |
| 8 | 6 |
| Entrada | Salida |
|---|---|
| -3 | 5 |
| 0 | 1 |
| 4 | 5 |
| Entrada | Salida |
|---|---|
| 1 | 0 |
| 5 | 2 |
| 5 | 4 |
Solución
Tabla\(\PageIndex{6}\) y Tabla\(\PageIndex{7}\) definen funciones. En ambos, cada valor de entrada corresponde exactamente a un valor de salida. Table\(\PageIndex{8}\) no define una función porque el valor de entrada de 5 corresponde a dos valores de salida diferentes.
Cuando una tabla representa una función, los valores de entrada y salida correspondientes también se pueden especificar usando la notación de función.
La función representada por Table se\(\PageIndex{6}\) puede representar por escrito
\[f(2)=1\text{, }f(5)=3\text{, and }f(8)=6 \nonumber\]
De igual manera, las declaraciones
\[g(−3)=5\text{, }g(0)=1\text{, and }g(4)=5 \nonumber\]
representan la función en la Tabla\(\PageIndex{7}\).
La tabla\(\PageIndex{8}\) no se puede expresar de manera similar porque no representa una función.
Ejercicio\(\PageIndex{5}\)
¿Table\(\PageIndex{9}\) representa una función?
| Entrada | Salida |
|---|---|
| 1 | 10 |
| 2 | 100 |
| 3 | 1000 |
- Contestar
-
si
Búsqueda de valores de entrada y salida de una función
Cuando conocemos un valor de entrada y queremos determinar el valor de salida correspondiente para una función, evaluamos la función. Evaluar siempre producirá un resultado porque cada valor de entrada de una función corresponde exactamente a un valor de salida.
Cuando conocemos un valor de salida y queremos determinar los valores de entrada que producirían ese valor de salida, establecemos la salida igual a la fórmula de la función y resolvemos para la entrada. La resolución puede producir más de una solución porque diferentes valores de entrada pueden producir el mismo valor de salida.
Evaluación de Funciones en Formas Algebraicas
Cuando tenemos una función en forma de fórmula, suele ser un asunto sencillo evaluar la función. Por ejemplo, la función se\(f(x)=5−3x^2\) puede evaluar elevando al cuadrado el valor de entrada, multiplicando por 3, y luego restando el producto de 5.
Cómo: Dada la fórmula para una función, evaluar.
Dada la fórmula para una función, evaluar.
- Reemplace la variable de entrada en la fórmula con el valor proporcionado.
- Calcular el resultado.
Ejemplo\(\PageIndex{6A}\): Evaluating Functions at Specific Values
1. Evaluar\(f(x)=x^2+3x−4\) en
- \(2\)
- \(a\)
- \(a+h\)
- Evaluar\(\frac{f(a+h)−f(a)}{h}\)
Solución
Reemplace la x en la función con cada valor especificado.
a. debido a que el valor de entrada es un número, 2, podemos usar álgebra simple para simplificar.
\[\begin{align*}f(2)&=2^2+3(2)−4\\&=4+6−4\\ &=6\end{align*}\]
b. En este caso, el valor de entrada es una letra por lo que no podemos simplificar más la respuesta.
\[f(a)=a^2+3a−4\nonumber\]
c. Con un valor de entrada de\(a+h\), debemos utilizar la propiedad distributiva.
\[\begin{align*}f(a+h)&=(a+h)^2+3(a+h)−4\\&=a^2+2ah+h^2+3a+3h−4 \end{align*}\]
d. En este caso, aplicamos los valores de entrada a la función más de una vez, para luego realizar operaciones algebraicas sobre el resultado. Ya encontramos que
\[f(a+h)=a^2+2ah+h^2+3a+3h−4\nonumber\]
y sabemos que
\[f(a)=a^2+3a−4 \nonumber\]
Ahora combinamos los resultados y simplificamos.
\[\begin{align*}\dfrac{f(a+h)−f(a)}{h}&=\dfrac{(a^2+2ah+h^2+3a+3h−4)−(a^2+3a−4)}{h}\\ &=\dfrac{(2ah+h^2+3h)}{h} \\ &=\dfrac{h(2a+h+3)}{h} & &\text{Factor out h.}\\ &=2a+h+3 & & \text{Simplify.}\end{align*}\]
Ejemplo\(\PageIndex{6B}\): Evaluating Functions
Dada la función\(h(p)=p^2+2p\), evaluar\(h(4)\).
Solución
Para evaluar\(h(4)\), sustituimos el valor 4 por la variable de entrada p en la función dada.
\[\begin{align*}h(p)&=p^2+2p\\h(4)&=(4)^2+2(4)\\ &=16+8\\&=24\end{align*}\]
Por lo tanto, para una entrada de 4, tenemos una salida de 24.
Ejercicio\(\PageIndex{6}\)
Dada la función\(g(m)=\sqrt{m−4}\), evaluar\(g(5)\).
- Contestar
-
\(g(5)=1\)
Ejemplo\(\PageIndex{7}\): Solving Functions
Dada la función\(h(p)=p^2+2p\), resolver para\(h(p)=3\).
Solución
\[\begin{array}{rl} h(p)=3\\p^2+2p=3 & \text{Substitute the original function}\\ p^2+2p−3=0 & \text{Subtract 3 from each side.}\\(p+3)(p−1)=0&\text{Factor.}\end{array} \nonumber \]
Si\((p+3)(p−1)=0\), cualquiera\((p+3)=0\) o\((p−1)=0\) (o ambos iguales\(0\)). Estableceremos cada factor igual a\(0\) y resolveremos para\(p\) en cada caso.
\[(p+3)=0,\; p=−3 \nonumber \]
\[(p−1)=0,\, p=1 \nonumber\]
Esto nos da dos soluciones. La salida\(h(p)=3\) cuando la entrada es\(p=1\) o\(p=−3\). También podemos verificar graficando como en la Figura\(\PageIndex{6}\). La gráfica verifica eso\(h(1)=h(−3)=3\) y\(h(4)=24\).
![[Gráfico de una parábola con puntos etiquetados (-3, 3), (1, 3) y (4, 24).]](https://math.libretexts.org/@api/deki/files/868/CNX_Precalc_Figure_01_01_006.jpg)
Ejercicio\(\PageIndex{7}\)
Dada la función\(g(m)=\sqrt{m−4}\), resolver\(g(m)=2\).
- Contestar
-
\(m=8\)
Evaluación de funciones expresadas en fórmulas
Algunas funciones se definen por reglas o procedimientos matemáticos expresados en forma de ecuación. Si es posible expresar la salida de la función con una fórmula que involucre la cantidad de entrada, entonces podemos definir una función en forma algebraica. Por ejemplo, la ecuación\(2n+6p=12\) expresa una relación funcional entre\(n\) y\(p\). Podemos reescribirlo para decidir si\(p\) es una función de\(n\).
Cómo: Dada una función en forma de ecuación, escribir su fórmula algebraica.
- Resuelve la ecuación para aislar la variable de salida en un lado del signo igual, con el otro lado como una expresión que involucra solo la variable de entrada.
- Utilice todos los métodos algebraicos habituales para resolver ecuaciones, como sumar o restar la misma cantidad hacia o desde ambos lados, o multiplicar o dividir ambos lados de la ecuación por la misma cantidad.
Ejemplo\(\PageIndex{8A}\): Finding an Equation of a Function
Expresar la relación\(2n+6p=12\) como una función\(p=f(n)\), si es posible.
Solución
Para expresar la relación en esta forma, necesitamos poder escribir la relación donde\(p\) es una función de\(n\), lo que significa escribirla como\(p=[\text{expression involving }n]\).
\[\begin{align*}2n+6p&=12 \\ 6p&=12−2n && \text{Subtract 2n from both sides.} \\ p&=\dfrac{12−2n}{6} & &\text{Divide both sides by 6 and simplify.} \\ p&=\frac{12}{6}−\frac{2n}{6} \\ p&=2−\frac{1}{3}n\end{align*}\]
Por lo\(p\) tanto, en función de\(n\) se escribe como
\[p=f(n)=2−\frac{1}{3}n \nonumber\]
Análisis
Es importante señalar que no todas las relaciones expresadas por una ecuación también pueden expresarse como una función con una fórmula.
Ejemplo\(\PageIndex{8B}\): Expressing the Equation of a Circle as a Function
¿La ecuación\(x^2+y^2=1\) representa una función con\(x\) como entrada y\(y\) como salida? Si es así, expresar la relación como una función\(y=f(x)\).
Solución
Primero restamos\(x^2\) de ambos lados.
\[y^2=1−x^2 \nonumber\]
Ahora tratamos de resolver para\(y\) en esta ecuación.
\[y=\pm\sqrt{1−x^2} \nonumber\]
\[\text{so, }y=\sqrt{1−x^2}\;\text{and}\;y = −\sqrt{1−x^2} \nonumber\]
Obtenemos dos salidas correspondientes a la misma entrada, por lo que esta relación no se puede representar como una sola función\(y=f(x)\).
Ejercicio\(\PageIndex{8}\)
Si\(x−8y^3=0\), expresar\(y\) en función de\(x\).
- Contestar
-
\(y=f(x)=\dfrac{\sqrt[3]{x}}{2}\)
Preguntas y respuestas
¿Hay relaciones expresadas por una ecuación que sí representan una función pero que aún no pueden ser representadas por una fórmula algebraica?
Sí, esto puede suceder. Por ejemplo, dada la ecuación\(x=y+2^y\), si queremos expresar y en función de x, no existe una fórmula algebraica simple que\(x\) implique solo eso es igual\(y\). Sin embargo, cada uno\(x\) determina un valor único para\(y\), y hay procedimientos matemáticos por los cuales se\(y\) pueden encontrar con cualquier precisión deseada. En este caso, decimos que la ecuación da una regla implícita (implícita) para\(y\) en función de\(x\), aunque la fórmula no se pueda escribir explícitamente.
Evaluación de una función dada en forma tabular
Como vimos anteriormente, podemos representar funciones en tablas. Por el contrario, podemos usar la información en tablas para escribir funciones, y podemos evaluar funciones usando las tablas. Por ejemplo, ¿qué tan bien recuerdan nuestras mascotas los buenos recuerdos que compartimos con ellas? Existe una leyenda urbana de que un pez dorado tiene un recuerdo de 3 segundos, pero esto es sólo un mito. Goldfish puede recordar hasta 3 meses, mientras que el pez beta tiene un recuerdo de hasta 5 meses. Y si bien el lapso de memoria de un cachorro no supera los 30 segundos, el perro adulto puede recordar durante 5 minutos. Esto es escaso en comparación con un gato, cuyo lapso de memoria dura 16 horas.
La función que relaciona el tipo de mascota con la duración de su lapso de memoria se visualiza más fácilmente con el uso de una tabla (Tabla\(\PageIndex{10}\)).
| Memoria para mascotas | lapso en horas |
|---|---|
| Cachorro | 0.008 |
| Perro Adulto | 0.083 |
| Cat | 3 |
| Goldfish | 2160 |
| Pez Beta | 3600 |
A veces, evaluar una función en forma de tabla puede ser más útil que usar ecuaciones. Aquí llamemos a la función\(P\). El dominio de la función es el tipo de mascota y el rango es un número real que representa el número de horas que dura la memoria de la mascota. Podemos evaluar la función\(P\) en el valor de entrada de “goldfish”. Nosotros escribiríamos\(P(goldfish)=2160\). Observe que, para evaluar la función en forma de tabla, identificamos el valor de entrada y el valor de salida correspondiente de la fila pertinente de la tabla. La forma tabular para la función P parece ideal para esta función, más que escribirla en forma de párrafo o función.
Cómo: Dada una función representada por una tabla, identificar valores específicos de salida y entrada
1. Encuentra la entrada dada en la fila (o columna) de los valores de entrada.
2. Identificar el valor de salida correspondiente emparejado con ese valor de entrada.
3. Encuentre los valores de salida dados en la fila (o columna) de los valores de salida, anotando cada vez que aparezca ese valor de salida.
4. Identificar los valores de entrada correspondientes al valor de salida dado.
Ejemplo\(\PageIndex{9}\): Evaluating and Solving a Tabular Function
Usando la tabla\(\PageIndex{11}\),
a. Evaluar\(g(3)\).
b. Resolver\(g(n)=6\).
| \(n\) | 1 | 2 | 3 | 4 | 5 |
| \(g(n)\) | 8 | 6 | 7 | 6 | 8 |
Solución
a. Evaluar\(g(3)\) significa determinar el valor de salida de la función\(g\) para el valor de entrada de\(n=3\). El valor de salida de la tabla correspondiente a\(n=3\) es 7, entonces\(g(3)=7\).
b. Resolver\(g(n)=6\) significa identificar los valores de entrada, n, que producen un valor de salida de 6. \(\PageIndex{12}\)El cuadro muestra dos soluciones: 2 y 4.
| \(n\) | 1 | 2 | 3 | 4 | 5 |
| \(g(n)\) | 8 | 6 | 7 | 6 | 8 |
Cuando ingresamos 2 en la función\(g\), nuestra salida es 6. Cuando ingresamos 4 en la función\(g\), nuestra salida también es 6.
Ejercicio\(\PageIndex{1}\)
Usando Tabla\(\PageIndex{12}\), evaluar\(g(1)\).
- Contestar
-
\(g(1)=8\)
Búsqueda de valores de función a partir de una gráfica
Evaluar una función usando una gráfica también requiere encontrar el valor de salida correspondiente para un valor de entrada dado, solo que en este caso, encontramos el valor de salida mirando la gráfica. Resolver una ecuación de función usando una gráfica requiere encontrar todas las instancias del valor de salida dado en la gráfica y observar los valores de entrada correspondientes.
Ejemplo\(\PageIndex{10}\): Reading Function Values from a Graph
Dada la gráfica de la Figura\(\PageIndex{7}\),
- Evaluar\(f(2)\).
- Resolver\(f(x)=4\).
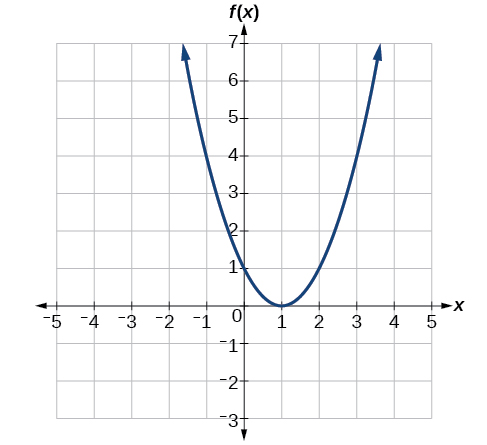
Solución
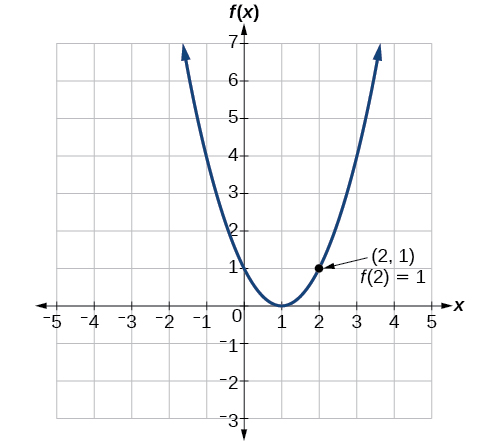
Para evaluar\(f(2)\), localice el punto en la curva donde\(x=2\), luego lea la coordenada y de ese punto. El punto tiene coordenadas\((2,1)\), entonces\(f(2)=1\). Ver Figura\(\PageIndex{8}\).
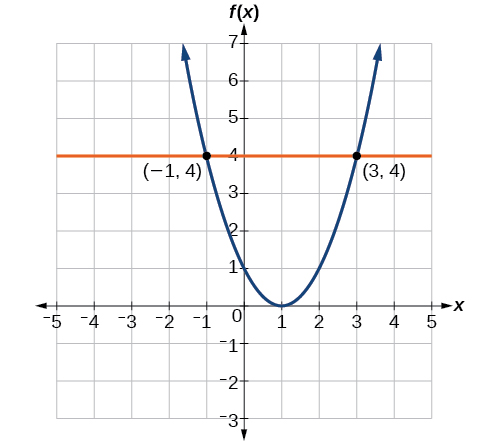
Para resolver\(f(x)=4\), encontramos el valor de salida 4 en el eje vertical. Moviéndose horizontalmente a lo largo de la línea\(y=4\), localizamos dos puntos de la curva con valor de salida 4:\((−1,4)\) y\((3,4)\). Estos puntos representan las dos soluciones a\(f(x)=4\): −1 ó 3. Esto significa\(f(−1)=4\) y\(f(3)=4\), o cuando la entrada es −1 o 3, la salida es 4. Ver Figura\(\PageIndex{9}\).
Ejercicio\(\PageIndex{10}\)
Dada la gráfica de la Figura\(\PageIndex{7}\), resuelva\(f(x)=1\).
- Contestar
-
\(x=0\)o\(x=2\)
Determinar si una función es uno a uno
Algunas funciones tienen un valor de salida dado que corresponde a dos o más valores de entrada. Por ejemplo, en el gráfico bursátil que se muestra en la Figura al inicio de este capítulo, el precio de las acciones fue de 1000 dólares en cinco fechas diferentes, lo que significa que hubo cinco valores de entrada diferentes que dieron como resultado el mismo valor de salida de 1000 dólares.
Sin embargo, algunas funciones tienen solo un valor de entrada por cada valor de salida, además de tener solo una salida para cada entrada. A estas funciones las llamamos funciones uno-a-uno. A modo de ejemplo, considere una escuela que utilice únicamente calificaciones de letras y equivalentes decimales, como se enumera en la Tabla\(\PageIndex{13}\).
| Grado de la Carta | Promedio del punto de grado |
|---|---|
| A | 4.0 |
| B | 3.0 |
| C | 2.0 |
| D | 1.0 |
Este sistema de calificación representa una función uno a uno, ya que cada entrada de letra produce una salida promedio de punto de calificación particular y cada promedio de punto de calificación corresponde a una letra de entrada.
Para visualizar este concepto, volvamos a ver las dos funciones simples esbozadas en Figuras\(\PageIndex{1a}\) y\(\PageIndex{1b}\). La función en la parte (a) muestra una relación que no es una función uno a uno porque las entradas\(q\) y\(r\) ambas dan salida\(n\). La función en la parte (b) muestra una relación que es una función uno a uno porque cada entrada está asociada con una sola salida.
Funciones uno a uno
Una función uno a uno es una función en la que cada valor de salida corresponde exactamente a un valor de entrada.
Ejemplo\(\PageIndex{11}\): Determining Whether a Relationship Is a One-to-One Function
¿El área de un círculo es función de su radio? En caso afirmativo, ¿la función es uno a uno?
Solución
Un círculo de radio\(r\) tiene una medida de área única dada por\(A={\pi}r^2\), así que para cualquier entrada\(r\),, solo hay una salida,\(A\). El área es una función del radio\(r\).
Si la función es uno a uno, el valor de salida, el área, debe corresponder a un valor de entrada único, el radio. Cualquier medida de área\(A\) viene dada por la fórmula\(A={\pi}r^2\). Debido a que las áreas y radios son números positivos, hay exactamente una solución:\(\sqrt{\frac{A}{\pi}}\). Entonces, el área de un círculo es una función uno a uno del radio del círculo.
Ejercicio\(\PageIndex{11A}\)
- ¿Un saldo es función del número de cuenta bancaria?
- ¿Un número de cuenta bancaria es función del saldo?
- ¿Es un saldo una función uno a uno del número de cuenta bancaria?
- Contestar
-
a. sí, porque cada cuenta bancaria tiene un saldo único en un momento dado;
b. no, porque varios números de cuentas bancarias pueden tener el mismo saldo;
c. no, porque la misma salida puede corresponder a más de una entrada.
Ejercicio\(\PageIndex{11B}\)
Evalúe lo siguiente:
- Si cada grado porcentual obtenido en un curso se traduce en calificación de una letra, ¿la calificación de la letra es una función de la calificación porcentual?
- Si es así, ¿la función es uno a uno?
- Contestar
-
a. Sí, la calificación de letras es una función del grado porcentual;
b. No, no es uno a uno. Hay 100 números por ciento diferentes que podríamos obtener pero solo alrededor de cinco calificaciones de letras posibles, por lo que no puede haber solo un número de uno por ciento que corresponda a cada grado de letra.
Uso de la Prueba de Línea Vertical
Como hemos visto en algunos ejemplos anteriores, podemos representar una función usando una gráfica. Los gráficos muestran una gran cantidad de pares de entrada-salida en un espacio pequeño. La información visual que proporcionan a menudo hace que las relaciones sean más fáciles de entender. Por convención, los gráficos se construyen típicamente con los valores de entrada a lo largo del eje horizontal y los valores de salida a lo largo del eje vertical.
Los gráficos más comunes nombran el valor de entrada\(x\) y la salida\(y\), y decimos que\(y\) es una función de\(x\), o\(y=f(x)\) cuando se nombra la función\(f\). La gráfica de la función es el conjunto de todos\((x,y)\) los puntos del plano que satisface la ecuación\(y=f(x)\). Si la función se define solo para unos pocos valores de entrada, entonces el gráfico de la función es solo de unos pocos puntos, donde la coordenada x de cada punto es un valor de entrada y la coordenada y de cada punto es el valor de salida correspondiente. Por ejemplo, los puntos negros en la gráfica de la Figura nos\(\PageIndex{10}\) dicen eso\(f(0)=2\) y\(f(6)=1\). Sin embargo, el conjunto de todos los puntos\((x,y)\) satisfactorios\(y=f(x)\) es una curva. La curva mostrada incluye\((0,2)\) y\((6,1)\) porque la curva pasa por esos puntos
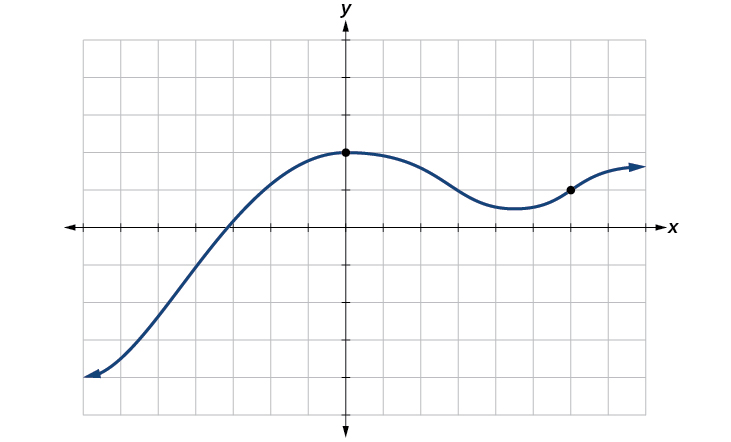
La prueba de línea vertical se puede utilizar para determinar si una gráfica representa una función. Si podemos dibujar cualquier línea vertical que intersecta una gráfica más de una vez, entonces la gráfica no define una función porque una función tiene solo un valor de salida por cada valor de entrada. Ver Figura\(\PageIndex{11}\).
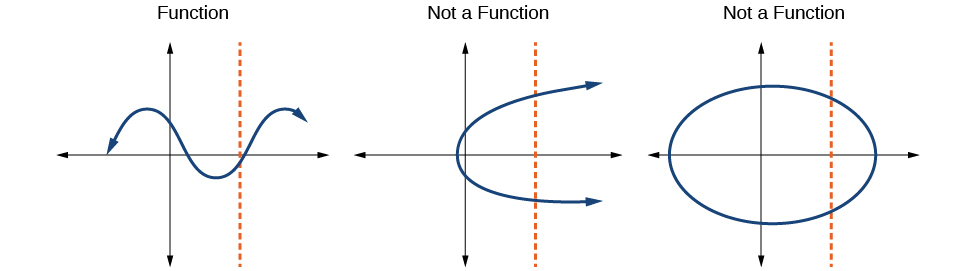
Cómo: Dado un gráfico, use la prueba de línea vertical para determinar si el gráfico representa una función
- Inspeccione la gráfica para ver si alguna línea vertical dibujada cruzaría la curva más de una vez.
- Si hay alguna línea de este tipo, determine que la gráfica no representa una función.
Ejemplo\(\PageIndex{12}\): Applying the Vertical Line Test
¿Cuál de las gráficas de la Figura\(\PageIndex{12}\) representa (s) una función\(y=f(x)\)?
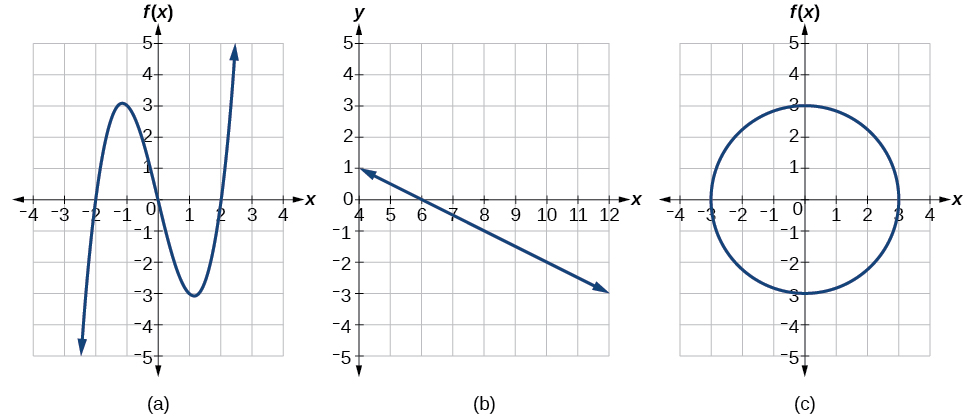
Solución
Si alguna línea vertical cruza una gráfica más de una vez, la relación representada por la gráfica no es una función. Observe que cualquier línea vertical pasaría por un solo punto de las dos gráficas mostradas en las partes (a) y (b) de la Figura\(\PageIndex{12}\). De esto podemos concluir que estas dos gráficas representan funciones. La tercera gráfica no representa una función porque, como máximo los valores x, una línea vertical cruzaría la gráfica en más de un punto, como se muestra en la Figura\(\PageIndex{13}\).
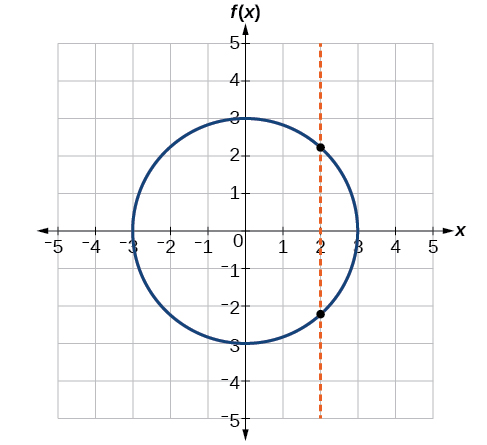
Ejercicio\(\PageIndex{12}\)
¿La gráfica de la Figura\(\PageIndex{14}\) representa una función?
![[Función absoluta f (x) =|x|.]](https://math.libretexts.org/@api/deki/files/885/CNX_Precalc_Figure_01_02_013.jpg)
- Contestar
-
si
Uso de la Prueba de Línea Horizontal
Una vez que hemos determinado que un gráfico define una función, una manera fácil de determinar si es una función uno a uno es usar la prueba de línea horizontal. Dibuja líneas horizontales a través de la gráfica. Si alguna línea horizontal cruza la gráfica más de una vez, entonces la gráfica no representa una función uno a uno.
Cómo: Dado un gráfico de una función, use la prueba de línea horizontal para determinar si el gráfico representa una función uno a uno
- Inspeccione la gráfica para ver si alguna línea horizontal dibujada cruzaría la curva más de una vez.
- Si hay alguna línea de este tipo, determine que la función no es uno a uno.
Ejemplo\(\PageIndex{13}\): Applying the Horizontal Line Test
Considere las funciones que se muestran en la Figura\(\PageIndex{12a}\) y Figura\(\PageIndex{12b}\). ¿Alguna de las funciones son una a una?
Solución
La función en la Figura no\(\PageIndex{12a}\) es uno a uno. La línea horizontal que se muestra en la Figura\(\PageIndex{15}\) cruza la gráfica de la función en dos puntos (e incluso podemos encontrar líneas horizontales que la cruzan en tres puntos).
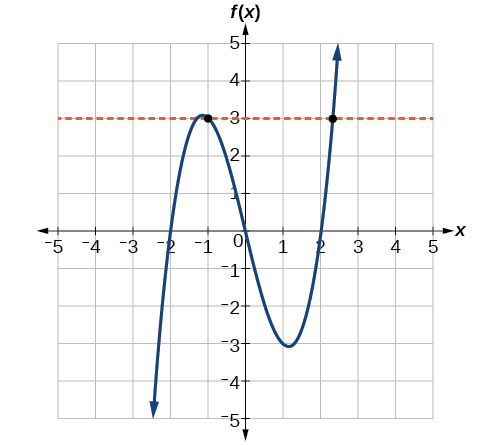
La función en la Figura\(\PageIndex{12b}\) es uno a uno. Cualquier línea horizontal cruzará una línea diagonal como máximo una vez.
Ejercicio\(\PageIndex{13}\)
¿La gráfica se muestra en la Figura\(\PageIndex{13}\) uno a uno?
- Contestar
-
No, porque no pasa la prueba de línea horizontal.
Identificación de las funciones básicas del kit
En este texto, exploraremos las funciones: las formas de sus gráficas, sus características únicas, sus fórmulas algebraicas y cómo resolver problemas con ellas. A la hora de aprender a leer, comenzamos con el alfabeto. Al aprender a hacer aritmética, comenzamos con números. Cuando se trabaja con funciones, es igualmente útil tener un conjunto base de elementos de bloque de construcción. A estas las llamamos nuestras “funciones del kit de herramientas”, que forman un conjunto de funciones básicas con nombre para las que conocemos la gráfica, la fórmula y las propiedades especiales. Algunas de estas funciones están programadas para botones individuales en muchas calculadoras. Para estas definiciones usaremos x como variable de entrada y\(y=f(x)\) como variable de salida.
Veremos estas funciones del kit de herramientas, combinaciones de funciones del kit de herramientas, sus gráficas y sus transformaciones con frecuencia a lo largo de este libro. Será muy útil si podemos reconocer estas funciones del kit de herramientas y sus características rápidamente por nombre, fórmula, gráfico y propiedades básicas de la tabla. Los gráficos y los valores de la tabla de muestra se incluyen con cada función mostrada en la Tabla\(\PageIndex{14}\).
| Nombre | Función | Gráfica |
|---|---|---|
| Constante | \(f(x)=c\)donde\(c\) es una constante |  |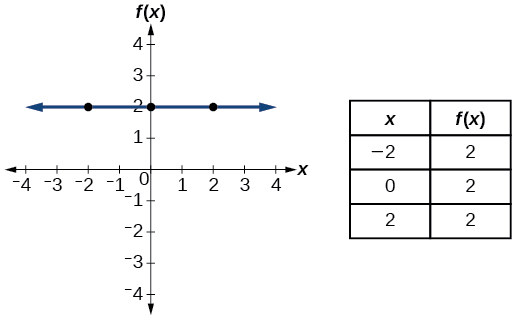
| Identidad | \(f(x)=x\) |  |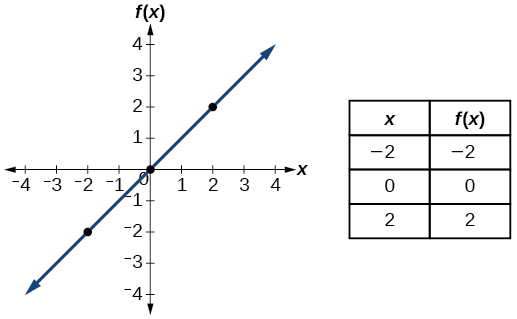
| Valor Absoluto | \(f(x)=|x|\) |  |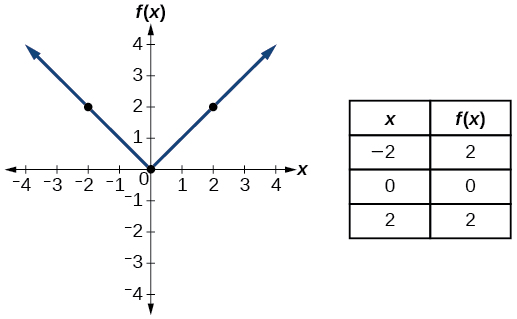
| Cuadrático | \(f(x)=x^2\) |  |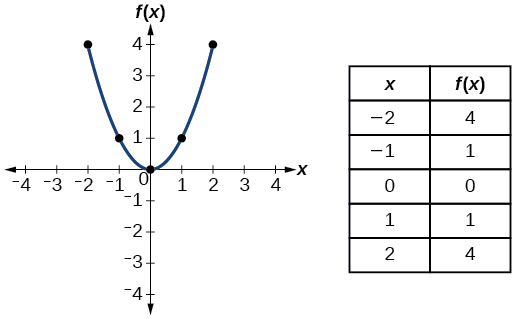
| Cúbico | \(f(x)=x^3\) |  |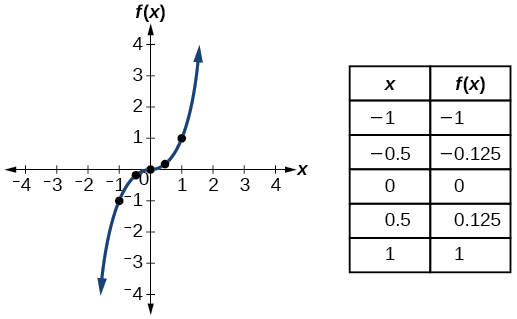
| recíproco | \(f(x)=\dfrac{1}{x}\) |  |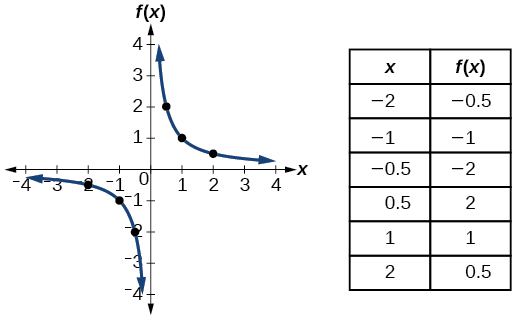
| Recíproco al cuadrado | \(f(x)=\dfrac{1}{x^2}\) |  |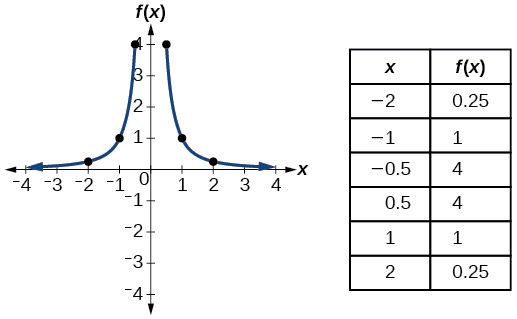
| Raíz cuadrada | \(f(x)=\sqrt{x}\) |  |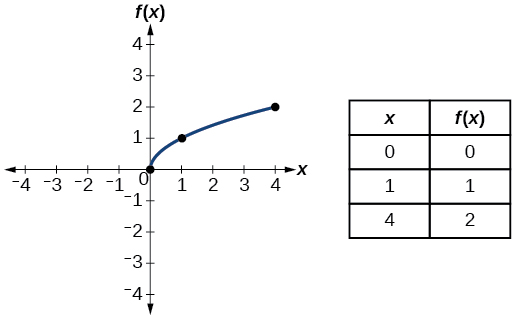
| Raíz cúbica | \(f(x)=\sqrt[3]{x}\) |  |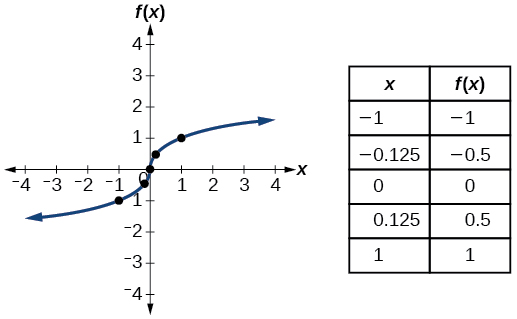
Ecuaciones Clave
- Función constante\(f(x)=c\), donde\(c\) es una constante
- Función de identidad\(f(x)=x\)
- Función de valor absoluto\(f(x)=|x|\)
- Función cuadrática\(f(x)=x^2\)
- Función cúbica\(f(x)=x^3\)
- Función recíproca\(f(x)=\dfrac{1}{x}\)
- Función al cuadrado recíproco\(f(x)=\frac{1}{x^2}\)
- Función de raíz cuadrada\(f(x)=\sqrt{x}\)
- Función de raíz cúbica\(f(x)=3\sqrt{x}\)
Conceptos clave
- Una relación es un conjunto de pares ordenados. Una función es un tipo específico de relación en la que cada valor de dominio, o entrada, conduce a exactamente un valor de rango, o salida.
- La notación de funciones es un método abreviado para relacionar la entrada con la salida en el formulario\(y=f(x)\).
- En forma tabular, una función puede ser representada por filas o columnas que se relacionan con valores de entrada y salida.
- Para evaluar una función, determinamos un valor de salida para un valor de entrada correspondiente. Las formas algebraicas de una función se pueden evaluar reemplazando la variable de entrada con un valor dado.
- Para resolver un valor de función específico, determinamos los valores de entrada que producen el valor de salida específico.
- Una forma algebraica de una función se puede escribir a partir de una ecuación.
- Los valores de entrada y salida de una función se pueden identificar a partir de una tabla.
- Relacionar los valores de entrada con los valores de salida en una gráfica es otra forma de evaluar una función.
- Una función es uno a uno si cada valor de salida corresponde a un solo valor de entrada.
- Un gráfico representa una función si alguna línea vertical dibujada en la gráfica se cruza con la gráfica en no más de un punto.
- El gráfico de una función uno a uno pasa la prueba de línea horizontal.
Notas al pie
1 http://www.baseball-almanac.com/lege... /lisn100.shtml. Accedido 24.03.2014.
2 www.kgbanswers.com/how-long-i... y-span/4221590. Accedido 24.03.2014.
Glosario
variable dependiente
una variable de salida
dominio
el conjunto de todos los valores de entrada posibles para una relación
función
una relación en la que cada valor de entrada produce un valor de salida único
prueba de línea horizontal
un método para probar si una función es uno a uno determinando si alguna línea horizontal interseca la gráfica más de una vez
variable independiente
una variable de entrada
introducir
cada objeto o valor en un dominio que se relaciona con otro objeto o valor mediante una relación conocida como función
función uno a uno
una función para la que cada valor de la salida está asociado con un valor de entrada único
generar
cada objeto o valor en el rango que se produce cuando se ingresa un valor de entrada en una función
variar
el conjunto de valores de salida que resultan de los valores de entrada en una relación
relación
un conjunto de pares ordenados
prueba de línea vertical
un método para probar si un gráfico representa una función determinando si una línea vertical interseca la gráfica no más de una vez