4.2: Funciones lineales

Objetivos de aprendizaje

• Representar una función lineal.
• Determine si una función lineal es creciente, decreciente o constante.
• Interpretar la pendiente como una tasa de cambio.
• Escribir e interpretar una ecuación para una función lineal.
• Gráfica funciones lineales.
• Determinar si las líneas son paralelas o perpendiculares.
• Escribe la ecuación de una línea paralela o perpendicular a una línea dada.

Al igual que con el crecimiento de una planta de bambú, hay muchas situaciones que implican un cambio constante a lo largo del tiempo. Consideremos, por ejemplo, el primer tren maglev comercial del mundo, el Tren MagLev de Shanghai (tren Maglev en el mundo, el Tren MagLev de Shanghái (Figura\(\PageIndex{1}\)). Lleva a los pasajeros cómodamente para un viaje de 30 kilómetros desde el aeropuerto hasta la estación del metro en solo ocho minutos.

Figura\(\PageIndex{1}\): Tren MagLev de Shanghái (crédito: “kanegen” /Flickr)

Supongamos que un tren maglev iba a recorrer una larga distancia, y que el tren mantiene una velocidad constante de 83 metros por segundo durante un periodo de tiempo una vez que se encuentra a 250 metros de la estación. ¿Cómo podemos analizar la distancia del tren a la estación en función del tiempo? En esta sección, investigaremos un tipo de función que sea útil para este propósito, y la usaremos para investigar situaciones del mundo real como la distancia del tren a la estación en un punto determinado en el tiempo.tren maglev iban a recorrer una larga distancia, y que el tren mantenga una velocidad constante de 83 metros por segundo por un periodo de tiempo una vez que esté a 250 metros de la estación. ¿Cómo podemos analizar la distancia del tren a la estación en función del tiempo? En esta sección, investigaremos un tipo de función que sea útil para este propósito, y la usaremos para investigar situaciones del mundo real como la distancia del tren a la estación en un momento dado.

Representando funciones lineales

La función que describe el movimiento del tren es una función lineal, que se define como una función con una tasa de cambio constante, es decir, un polinomio de grado 1. Hay varias formas de representar una función lineal, incluyendo la forma de la palabra, la notación de función, la forma tabular y la forma gráfica. Describiremos el movimiento del tren como una función utilizando cada método.

Representación de una función lineal en forma de palabra

Comencemos describiendo la función lineal en palabras. Para el problema del tren que acabamos de considerar, se puede usar la siguiente frase de palabra para describir la relación de función.

• La distancia del tren a la estación es función del tiempo durante el cual el tren se mueve a una velocidad constante más su distancia original de la estación cuando comenzó a moverse a velocidad constante.

La velocidad es la tasa de cambio. Recordemos que una tasa de cambio es una medida de la rapidez con la que cambia la variable dependiente con respecto a la variable independiente. La tasa de cambio para este ejemplo es constante, lo que significa que es la misma para cada valor de entrada. A medida que el tiempo (entrada) aumenta en 1 segundo, la distancia correspondiente (salida) aumenta en 83 metros. El tren comenzó a moverse a esta velocidad constante a una distancia de 250 metros de la estación.

Representación de una función lineal en notación de funciones

Otro enfoque para representar funciones lineales es mediante el uso de la notación de funciones. Un ejemplo de notación de función es una ecuación escrita en la forma conocida como la forma pendiente-intercepción de una línea, donde xes el valor de entrada,\(m\) es la tasa de cambio, y\(b\) es el valor inicial de la variable dependiente.

\[\begin{align*} &\text{Equation form } &y=mx+b \\[4pt] &\text{Equation notation } &f(x)=mx+b \end{align*}\]

En el ejemplo del tren, podríamos usar la notación\(D(t)\) en la que la distancia total\(D\) es una función del tiempo\(t\). La tasa,\(m\), es de 83 metros por segundo. El valor inicial de la variable dependiente\(b\) es la distancia original de la estación, 250 metros. Podemos escribir una ecuación generalizada para representar el movimiento del tren.

\[D(t)=83t+250\]

Representación de una función lineal en forma tabular

Un tercer método para representar una función lineal es mediante el uso de una tabla. La relación entre la distancia desde la estación y el tiempo se representa en la Figura\(\PageIndex{2}\). De la tabla, podemos ver que la distancia cambia 83 metros por cada incremento de tiempo de 1 segundo.

\ (t\), que contiene los segundos de 0 a 3, y con la segunda fila, etiquetada\(D(t)\), que contiene los metros 250 a 499. La primera fila sube 1 segundo, y la segunda fila sube 83 metros.” src=” https://math.libretexts.org/@api/dek..._02_01_015.jpg "fileid="1058" />

Figura\(\PageIndex{2}\): Representación tabular de la función\(D\) que muestra los valores de entrada y salida seleccionados

Q/A? ¿Puede la entrada en el ejemplo anterior ser algún número real?

No. La entrada representa el tiempo, por lo que si bien los números racionales e irracionales no negativos son posibles, los números reales negativos no son posibles para este ejemplo. La entrada consiste en números reales no negativos.

Representación de una función lineal en forma gráfica

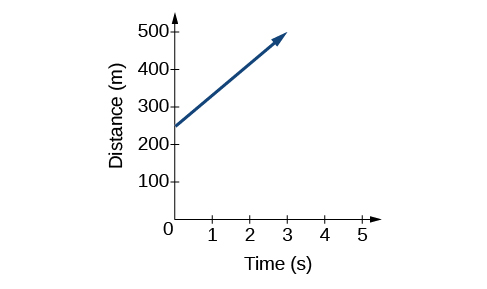
Otra forma de representar funciones lineales es visualmente, usando una gráfica. Podemos utilizar la relación de función desde arriba,\(D(t)=83t+250\), para dibujar una gráfica, representada en la Figura\(\PageIndex{3}\). Observe que la gráfica es una línea. Cuando trazamos una función lineal, la gráfica es siempre una línea.

La tasa de cambio, que es constante, determina la inclinación o pendiente de la línea. El punto en el que el valor de entrada es cero es la intercepción vertical, o intercepción y, de la línea. Podemos ver en la gráfica de la Figura\(\PageIndex{3}\) que la intercepción y en el ejemplo del tren que acabamos de ver es\((0,250)\) y representa la distancia del tren desde la estación cuando comenzó a moverse a una velocidad constante.

Figura\(\PageIndex{3}\): La gráfica de\(D(t)=83t+250\). Las gráficas de funciones lineales son líneas porque la velocidad de cambio es constante.

Observe que la gráfica del ejemplo de tren está restringida, pero no siempre es así. Considera la gráfica de la línea\(f(x)=2x+1\). Pregúntate qué números se pueden ingresar a la función, es decir, ¿cuál es el dominio de la función? El dominio está compuesto por todos los números reales porque cualquier número puede duplicarse, y luego tener uno agregado al producto.

Definición: Función lineal

Una función lineal es una función cuya gráfica es una línea. Las funciones lineales se pueden escribir en forma de pendiente-intercepción de una línea

\[f(x)=mx+b\]

donde\(b\) es el valor inicial o inicial de la función (cuando se introduce,\(x=0\)), y\(m\) es la tasa constante de cambio, o pendiente de la función. La intercepción y está en\((0,b)\).

Ejemplo\(\PageIndex{1}\): Using a Linear Function to Find the Pressure on a Diver

La presión,\(P\), en libras por pulgada cuadrada (PSI) sobre el buzo en la Figura\(\PageIndex{4}\) depende de su profundidad por debajo de la superficie del agua\(d\),, en pies. Esta relación puede ser modelada por la ecuación,\(P(d)=0.434d+14.696\). Reafirmar esta función en palabras.

Figura\(\PageIndex{4}\): (crédito: Ilse Reijs y Jan-Noud Hutten) Hutten)

Para reafirmar la función en palabras, necesitamos describir cada parte de la ecuación. La presión en función de la profundidad equivale a cuatrocientos treinta y cuatro milésimas veces la profundidad más catorce seiscientos noventa y seis milésimas.

Análisis

El valor inicial, 14.696, es la presión en PSI sobre el buceador a una profundidad de 0 pies, que es la superficie del agua. La tasa de cambio, o pendiente, es de 0.434 PSI por pie. Esto nos dice que la presión sobre el buceador aumenta 0.434 PSI por cada pie que aumenta su profundidad.

Determinar si una función lineal aumenta, disminuye o es constante

Las funciones lineales que usamos en los dos ejemplos anteriores aumentaron con el tiempo, pero no todas las funciones lineales lo hacen. Una función lineal puede ser creciente, decreciente o constante. Para una función creciente, como en el ejemplo del tren, los valores de salida aumentan a medida que aumentan los valores de entrada. La gráfica de una función creciente tiene una pendiente positiva. Una línea con pendiente positiva se inclina hacia arriba de izquierda a derecha como en la Figura\(\PageIndex{5}\) (a). Para una función decreciente, la pendiente es negativa. Los valores de salida disminuyen a medida que aumentan los valores de entrada. Una línea con pendiente negativa se inclina hacia abajo de izquierda a derecha como en la Figura\(\PageIndex{5}\) (b). Si la función es constante, los valores de salida son los mismos para todos los valores de entrada por lo que la pendiente es cero. Una línea con una pendiente de cero es horizontal como en la Figura\(\PageIndex{5}\) (c).

Figura\(\PageIndex{5}\): Tres gráficas que representan una función creciente, una función decreciente y una función constante.]
Funciones crecientes y decrecientes

Funciones crecientes y decrecientes

La pendiente determina si la función es una función lineal creciente, una función lineal decreciente o una función constante.

• \(f(x)=mx+b\)es una función creciente si\(m>0\).
• \(f(x)=mx+b\)es una función decreciente si\(m<0\).
• \(f(x)=mx+b\)es una función constante si\(m=0\).

Ejemplo\(\PageIndex{2}\): Deciding whether a Function Is Increasing, Decreasing, or Constant

Algunos estudios recientes sugieren que un adolescente envía un promedio de 60 textos diarios. Para cada uno de los siguientes escenarios, busque la función lineal que describe la relación entre el valor de entrada y el valor de salida. Luego, determine si la gráfica de la función es creciente, decreciente o constante.

1. El número total de textos que envía un adolescente se considera una función del tiempo en días. La entrada es el número de días, y la salida es el número total de textos enviados.
2. Un adolescente tiene un límite de 500 textos mensuales en su plan de datos. La entrada es el número de días, y la salida es el número total de textos restantes para el mes.
3. Un adolescente tiene un número ilimitado de textos en su plan de datos por un costo de $50 mensuales. La entrada es el número de días, y la salida es el costo total de enviar mensajes de texto cada mes.

Solución

Analizar cada función.

1. La función se puede representar como\(f(x)=60x\) donde\(x\) está el número de días. La pendiente, 60, es positiva por lo que la función va en aumento. Esto tiene sentido porque el número total de textos aumenta con cada día.
2. La función se puede representar como\(f(x)=500−60x\) donde\(x\) está el número de días. En este caso, la pendiente es negativa por lo que la función es decreciente. Esto tiene sentido porque el número de textos restantes disminuye cada día y esta función representa el número de textos que quedan en el plan de datos después de\(x\) días.
3. La función de costo se puede representar como\(f(x)=50\) porque el número de días no afecta el costo total. La pendiente es 0 por lo que la función es constante.

Cálculo e Interpretación de Talud

En los ejemplos que hemos visto hasta ahora, se nos ha proporcionado la pendiente. Sin embargo, a menudo necesitamos calcular la pendiente dados los valores de entrada y salida. Dados dos valores para la entrada,\(x_1\) y\(x_2\), y dos valores correspondientes para la salida,\(y_1\) y\(y_2\) —que pueden ser representados por un conjunto de puntos,\((x_1,y_1)\) y\((x_2,y_2)\) —podemos calcular la pendiente\(m\), de la siguiente manera

\[\begin{align*} m &= \dfrac{\text{change in output (rise)}}{ \text{change in input (run)}} \\[4pt] &= \dfrac{{\Delta}y}{ {\Delta}x} = \dfrac{y_2−y_1}{x_2−x_1} \end{align*}\]

donde\({\Delta}y\) está el desplazamiento vertical y\({\Delta}x\) es el desplazamiento horizontal. Nota en notación de función dos valores correspondientes para la salida\(y_1\) y\(y_2\) para la función\(f\),\(y_1=f(x_1)\) y\(y_2=f(x_2)\), así podríamos escribir de manera equivalente

\[m=\dfrac{f(x_2)-f(x_1)}{x_2-x_1} \nonumber\]

La figura\(\PageIndex{6}\) indica cómo se calcula la pendiente de la línea entre los puntos\((x_2,y_2)\),\((x_1,y_1)\) y,. Recordemos que la pendiente mide la inclinación. Cuanto mayor sea el valor absoluto de la pendiente, más pronunciada es la línea.

Figura\(\PageIndex{6}\): La pendiente de una función se calcula por el cambio en\(y\) dividido por el cambio en\(x\). No importa qué coordenada se utilice como la\((x_2,y_2)\) y cuál es la\((x_1 ,y_1)\), siempre y cuando cada cálculo se inicie con los elementos del mismo par de coordenadas.

Q & A

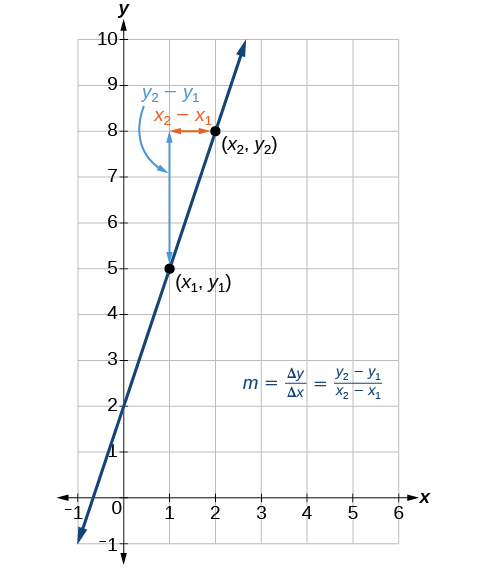
¿Las unidades para pendiente son siempre\(\frac{\text{units for the output}}{ \text{units for the input}}\)?

Sí. Piense en las unidades como el cambio del valor de salida para cada unidad de cambio en el valor de entrada. Un ejemplo de pendiente podría ser millas por hora o dólares por día. Observe que las unidades aparecen como una relación de unidades para la salida por unidades para la entrada.

Calcular pendiente

La pendiente, o tasa de cambio, de una función se\(m\) puede calcular de acuerdo con lo siguiente:

\[m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{{\Delta}y}{{\Delta}x}=\dfrac{y_2-y_1}{x_2-x_1}\]

donde\(x_1\) y\(x_2\) son valores de entrada,\(y_1\) y\(y_2\) son valores de salida.

Dados dos puntos de una función lineal, calcular e interpretar la pendiente.

1. Determine las unidades para los valores de salida y entrada.
2. Calcular el cambio de los valores de salida y el cambio de los valores de entrada.
3. Interpretar la pendiente como el cambio en los valores de salida por unidad del valor de entrada.

Ejemplo\(\PageIndex{3}\): Finding the Slope of a Linear Function

Si\(f(x)\) es una función lineal, y\((3,−2)\) y\((8,1)\) son puntos en la línea, encuentra la pendiente. ¿Esta función está aumentando o disminuyendo?

Solución

Los pares de coordenadas son\((3,−2)\) y\((8,1)\). Para encontrar la tasa de cambio, dividimos el cambio en la salida por el cambio en la entrada.

\[m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{1-(-2)}{8-3}=\dfrac{3}{5}\]

También podríamos escribir la pendiente como\(m=0.6\). La función va en aumento porque\(m>0\).

Análisis

Como se señaló anteriormente, el orden en que escribimos los puntos no importa cuando calculamos la pendiente de la línea siempre y cuando el primer valor de salida, o coordenada y, utilizado corresponda con el primer valor de entrada, o coordenada x, usado.

¡Pruébalo! \(\PageIndex{1}\)

Si\(f(x)\) es una función lineal, y\((2, 3)\) y\((0,4)\) son puntos en la línea, encuentra la pendiente. ¿Esta función está aumentando o disminuyendo?

Contestar

\(m=\frac{4−3}{0−2} =\frac{1}{-2}=-\frac{1}{2}\); decreciente porque\(m<0\).

Ejemplo\(\PageIndex{4}\): Finding the Population Change from a Linear Function

La población de una ciudad aumentó de 23,400 a 27,800 entre 2008 y 2012. Encontrar el cambio de población por año si asumimos que el cambio fue constante de 2008 a 2012.

La tasa de cambio relaciona el cambio en la población con el cambio en el tiempo. La población aumentó en\(27,800−23,400=4400\) personas durante el intervalo de tiempo de cuatro años. Para encontrar la tasa de cambio, divida el cambio en el número de personas por el número de años.

\[\dfrac{4,400 \text{ people}}{4 \text{ years}} =1,100 \dfrac{\text{people}}{\text{year}}\]

Por lo que la población aumentó en mil 100 personas al año.

Análisis

Debido a que nos dicen que la población aumentó, esperaríamos que la pendiente fuera positiva. Esta pendiente positiva que calculamos es, por lo tanto, razonable.

¡Pruébalo! \(\PageIndex{2}\)

La población de un pequeño pueblo aumentó de 1,442 a 1,868 entre 2009 y 2012. Encontrar el cambio de población por año si asumimos que el cambio fue constante de 2009 a 2012.

Contestar

\(m=\frac{1,868−1,442}{2,012−2,009} = \frac{426}{3} =\text{ 142 people per year}\)

Escribir la forma de punto-pendiente de una ecuación lineal

Hasta ahora, hemos estado usando la forma pendiente-intercepción de una ecuación lineal para describir funciones lineales. Aquí aprenderemos otra forma de escribir una función lineal, la forma punto-pendiente.

\[y-y_1=m(x-x_1)\]

La forma punto-pendiente se deriva de la fórmula de pendiente.

\[ \begin{align*} &m=\dfrac{y-y_1}{x-x_1} &\text{assuming }x{\neq}x_1 \\ &m(x-x_1)=\dfrac{y-y_1}{x-x_1}(x-x_1) &\text{Multiply both sides by }(x-x_1). \\ &m(x-x_1)=y-y_1 &\text{Simplify} \\ &y-y_1=m(x-x_1) &\text{Rearrange} \end{align*}\]

Tenga en cuenta que la forma pendiente-intercepción y la forma punto-pendiente se pueden utilizar para describir la misma función. Podemos pasar de una forma a otra usando álgebra básica. Por ejemplo, supongamos que se nos da una ecuación en forma de punto-pendiente,\(y−4=− \frac{1}{2}(x−6)\). Podemos convertirlo a la forma pendiente-intercepción como se muestra.

\[\begin{align*} y-4&=-\dfrac{1}{2}(x-6) \\ y-4&=-\dfrac{1}{2}x+3 &\text{Distribute the }-\dfrac{1}{2}. \\ y&=-\dfrac{1}{2}x+7 &\text{Add 4 to each side.}\end{align*}\]

Por lo tanto, la misma línea se puede describir en forma de pendiente-intercepción como\(y=\dfrac{1}{2}x+7\).

Forma Punto-Pendiente de una Ecuación Lineal

La forma punto-pendiente de una ecuación lineal toma la forma

\[y-y_1=m(x−x_1)\]

donde\(m\) está la pendiente,\(x_1\) y\(y_1\) son las\(y\) coordenadas\(x\) y de un punto específico por el que pasa la línea.

Escribir la ecuación de una línea usando un punto y el talud

La forma punto-pendiente es particularmente útil si conocemos un punto y la pendiente de una línea. Supongamos, por ejemplo, se nos dice que una línea tiene una pendiente de 2 y pasa por el punto\((4,1)\). Sabemos eso\(m=2\) y eso\(x_1=4\) y\(y_1=1\). Podemos sustituir estos valores en la ecuación general de punto-pendiente.

\[\begin{align*} y−y_1&=m(x−x_1) \\ y−1&=2(x−4) \end{align*}\]

Si quisiéramos entonces reescribir la ecuación en forma de pendiente-intercepción, aplicamos técnicas algebraicas.

\[\begin{align*} y−1&=2(x−4) \\ y−1&=2x−8 &\text{Distribute the 2.} \\ y&=2x−7 &\text{Add 1 to each side.} \end{align*}\]

Ambas ecuaciones,\(y−1=2(x−4)\) y\(y=2x–7\), describen la misma línea. Ver Figura\(\PageIndex{7}\).

Figura\(\PageIndex{7}\)

Ejemplo\(\PageIndex{5}\): Writing Linear Equations Using a Point and the Slope

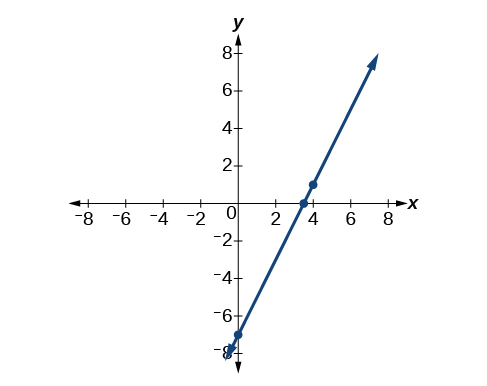
Escribe la forma punto-pendiente de una ecuación de una línea con una pendiente de 3 que pasa por el punto\((6,–1)\). Después reescribirlo en la forma pendiente-intercepción.

Solución

Averiguemos lo que sabemos de la información dada. La pendiente es de 3, entonces\(m=3\). También conocemos un punto, entonces sabemos\(x_1=6\) y\(y_1 =−1\). Ahora podemos sustituir estos valores en la ecuación general de punto-pendiente.

\[\begin{align*} y-y_1&=m(x-x_1) \\ y−(−1)&=3(x−6) &\text{Substitute known values.} \\ y+1&=3(x−6) &\text{Distribute −1 to find point-slope form.} \end{align*}\]

Entonces usamos álgebra para encontrar la forma pendiente-intercepción.

\[\begin{align*} y+1&=3(x−6) \\ y+1&=3x−18 &\text{Distribute 3.} \\ y&=3x−19 &\text{Simplify to slope-intercept form.} \end{align*}\]

¡Pruébalo! \(\PageIndex{3}\)

Escriba la forma punto-pendiente de una ecuación de una línea con una pendiente de —2 que pasa por el punto\((–2, 2)\). Después reescribirlo en la forma pendiente-intercepción.

Contestar

\(y−2=−2(x+2)\);\(y=−2x−2\)

Escribir la ecuación de una línea usando dos puntos

La forma punto-pendiente de una ecuación también es útil si conocemos dos puntos a través de los cuales pasa una línea. Supongamos, por ejemplo, sabemos que una línea pasa por los puntos\((0, 1)\) y\((3, 2)\). Podemos usar las coordenadas de los dos puntos para encontrar la pendiente.

\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{2-1}{3-0} \\ &=\dfrac{1}{3} \end{align*}\]

Ahora podemos usar la pendiente que encontramos y las coordenadas de uno de los puntos para encontrar la ecuación para la línea. Déjanos usar\((0,1)\) para nuestro punto.

\[\begin{align*} y-y_1&=m(x-x_1) \\ y-1&=\dfrac{1}{3}(x-0) \end{align*}\]

Como antes, podemos usar álgebra para reescribir la ecuación en la forma pendiente-intercepción.

\[\begin{align*} y-1&=\dfrac{1}{3}(x-0) \\ y-1&=\dfrac{1}{3}x &\text{Distribute the }\dfrac{1}{3}. \\ y&=\dfrac{1}{3}x+1 &\text{Add 1 to each side.} \end{align*}\]

Ambas ecuaciones describen la línea mostrada en la Figura\(\PageIndex{8}\).

Figura\(\PageIndex{8}\)

Ejemplo\(\PageIndex{6}\): Writing Linear Equations Using Two Points

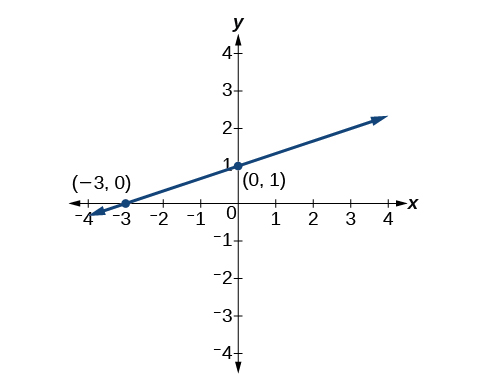
Escribe la forma punto-pendiente de una ecuación de una línea que pasa por los puntos\((5,1)\) y\((8, 7)\). Después reescribirlo en la forma pendiente-intercepción.

Empecemos por encontrar la pendiente.

\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{7-1}{8-5} \\ &=\dfrac{6}{3} \\ &= 2 \end{align*}\]

Entonces\(m=2\). A continuación, sustituimos la pendiente y las coordenadas por uno de los puntos en la ecuación general de pendiente puntual. Podemos elegir cualquiera de los dos puntos, pero vamos a utilizar\((5,1)\).

\[\begin{align*} y-y_1&=m(x-x_1) \\ y-1&=2(x-5) \end{align*}\]

La ecuación de punto-pendiente de la línea es\(y_2–1=2(x_2–5)\). Para reescribir la ecuación en forma pendiente-intercepción, utilizamos álgebra.

\[\begin{align*} y-1&=2(x-5) \\ y-1&=2x-10 \\ y&=2x-9 \end{align*}\]

La ecuación pendiente-intercepción de la línea es\(y=2x–9\).

\(\PageIndex{4}\): Escribir la forma punto-pendiente de una ecuación de una línea que pasa por los puntos\((–1,3)\) y\((0,0)\). Después reescribirlo en la forma pendiente-intercepción.

Solución

\(y−0=−3(x−0)\);\(y=−3x\)

Escribir e interpretar una ecuación para una función lineal

Ahora que hemos escrito ecuaciones para funciones lineales tanto en la forma pendiente-intercepción como en la forma punto-pendiente, podemos elegir qué método usar en función de la información que se nos da. Esa información puede ser proporcionada en forma de gráfica, punto y pendiente, dos puntos, y así sucesivamente. Mira la gráfica de la función\(f\) en la Figura\(\PageIndex{9}\).

Figura\(\PageIndex{9}\): Gráfica que representa cómo calcular la pendiente de una línea.

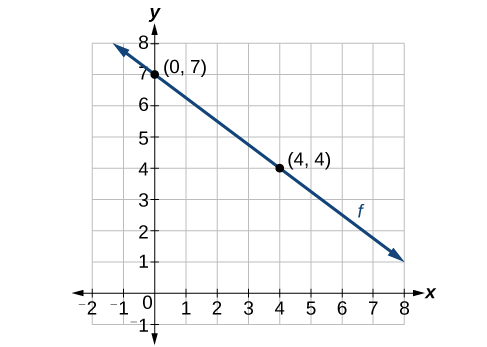
No se nos da la pendiente de la línea, pero podemos elegir dos puntos cualesquiera en la línea para encontrar la pendiente. Vamos a elegir\((0,7)\) y\((4, 4)\). Podemos utilizar estos puntos para calcular la pendiente.

\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{4-7}{4-0} \\&=-\dfrac{3}{4}\end{align*}\]

Ahora podemos sustituir la pendiente y las coordenadas de uno de los puntos en la forma punto-pendiente.

\[\begin{align*} y-y_1&=m(x-x_1) \\ y-4&=-\dfrac{3}{4}(x-4) \end{align*}\]

Si queremos reescribir la ecuación en la forma pendiente-intercepción, encontraríamos

\[\begin{align*} y-4&=-\dfrac{3}{4}(x-4) \\ y-4 &=-\dfrac{3}{4}x+3 \\ y&=-\dfrac{3}{4}x+7\end{align*}\]

Si quisiéramos encontrar la forma pendiente-intercepción sin escribir primero la forma de punto-pendiente, podríamos haber reconocido que la línea cruza el eje y cuando el valor de salida es 7. Por lo tanto,\(b=7\). Ahora tenemos el valor inicial\(b\) y la pendiente\(m\) para que podamos sustituir\(m\) y\(b\) en la forma pendiente-intercepción de una línea.

Figura\(\PageIndex{10}\)

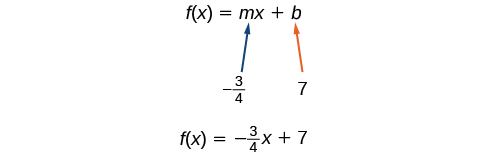
Entonces la función es\(f(x)=−\frac{3}{4}x+7\), y la ecuación lineal sería\(y=−\frac{3}{4}x+7\).

Dada la gráfica de una función lineal, escribir una ecuación para representar la función.

1. Identificar dos puntos en la línea.
2. Usa los dos puntos para calcular la pendiente.
3. Determinar dónde la línea cruza el eje y para identificar la intercepción y mediante inspección visual.
4. Sustituya la pendiente y la intercepción y en la forma pendiente-intercepción de una ecuación de línea.

Ejemplo\(\PageIndex{7}\): Writing an Equation for a Linear Function

Escribe una ecuación para una función lineal dada una gráfica de la que\(f\) se muestra en la Figura\(\PageIndex{11}\).

Figura\(\PageIndex{11}\)

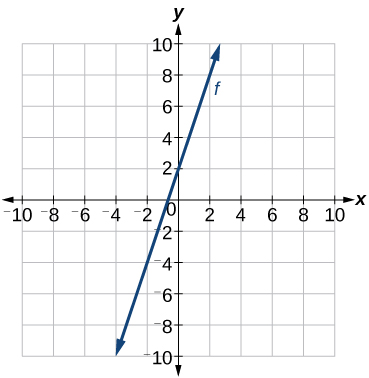
Solución

Identificar dos puntos en la línea, como\((0, 2)\) y\((−2,−4)\). Usa los puntos para calcular la pendiente.

\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{4-2}{-2-0} \\ &=\dfrac{-6}{-2} \\ &=3 \end{align*}\]

Sustituya el talud y las coordenadas de uno de los puntos en la forma punto-pendiente.

\[\begin{align*} y-y_1&=m(x-x_1) \\ y-(-4)&=3(x-(-2)) \\ y+4 &= 3(x+2)\end{align*}\]

Podemos usar álgebra para reescribir la ecuación en la forma pendiente-intercepción.

\[\begin{align*} y+4&= 3(x+2) \\ y+4&= 3x+6 \\ y & = 3x + 2 \end{align*}\]

Análisis

Esto tiene sentido porque podemos ver en Figura\(\PageIndex{12}\) que la línea cruza el eje y en el punto\((0, 2)\), que es la intercepción y, entonces\(b=2\).

Figura\(\PageIndex{12}\): Gráfico de una línea creciente con puntos en\((0, 2)\) y\((-2, -4)\).

Ejemplo\(\PageIndex{8}\): Writing an Equation for a Linear Cost Function

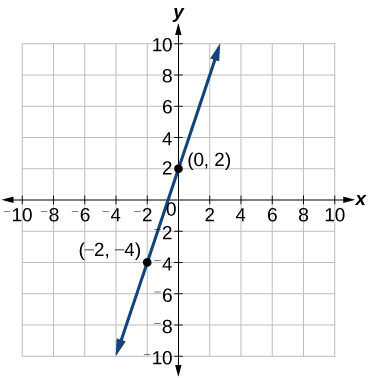
Supongamos que Ben inicia una empresa en la que incurre en un costo fijo de $1,250 mensuales por los gastos generales, que incluye la renta de su oficina. Sus costos de producción son de 37.50 dólares por artículo. Escribe una función lineal\(C\) donde\(C(x)\) está el costo de los\(x\) artículos producidos en un mes determinado.

Solución

El costo fijo está presente cada mes, $1,250. Los costos que pueden variar incluyen el costo para producir cada artículo, que es $37.50 para Ben. El costo variable, denominado costo marginal, está representado por 37.5. El costo en el que incurre Ben es la suma de estos dos costos, representados por\(C(x)=1250+37.5x\).

Análisis

Si Ben produce 100 artículos en un mes, su costo mensual está representado por

\[\begin{align*} C(100)&=1250+37.5(100) \\ &=5000 \end{align*}\]

Por lo que su costo mensual sería de 5.000 dólares.

Ejemplo\(\PageIndex{9}\): Writing an Equation for a Linear Function Given Two Points

Si\(f\) es una función lineal, con\(f(3)=−2\), y\(f(8)=1\), encontrar una ecuación para la función en forma pendiente-intercepción.

Solución

Podemos escribir los puntos dados usando coordenadas.

\[\begin{align*} f(3)&= -2{\rightarrow}(3,2) \\ f(8)&=1{\rightarrow}(8,1) \end{align*}\]

Entonces podemos usar los puntos para calcular la pendiente.

\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{1-(-2)}{8-3} \\ &=\dfrac{3}{5} \end{align*}\]

Sustituya el talud y las coordenadas de uno de los puntos en la forma punto-pendiente.

\[\begin{align*} y-y_1&=m(x-x_1) \\ y-(-2)&=\dfrac{3}{5}(x-3) \end{align*}\]

Podemos usar álgebra para reescribir la ecuación en la forma pendiente-intercepción.

\[\begin{align*} y+2&=\dfrac{3}{5}(x-3) \\ y+2&=\dfrac{3}{5}x-\dfrac{9}{5} \\ y&=\dfrac{3}{5}x-\dfrac{19}{5} \end{align*}\]

¡Tri It! \(\PageIndex{1}\)

Si\(f(x)\) es una función lineal, con\(f(2)=–11\), y\(f(4)=−25\), encontrar una ecuación para la función en forma pendiente-intercepción.

Contestar

\(y=−7x+3\)

Modelado de problemas del mundo real con funciones lineales

En el mundo real, los problemas no siempre se enuncian explícitamente en términos de una función o se representan con una gráfica. Afortunadamente, podemos analizar el problema representándolo primero como una función lineal y luego interpretando los componentes de la función. Mientras sepamos, o podamos averiguar, el valor inicial y la tasa de cambio de una función lineal, podemos resolver muchos tipos diferentes de problemas del mundo real.

Dada una función lineal\(f\) y el valor inicial y la tasa de cambio, evaluar\(f(c)\).

1. Determinar el valor inicial y la tasa de cambio (pendiente).
2. Sustituir los valores en\(f(x)=mx+b\).
3. Evaluar la función en\(x=c\).

Ejemplo\(\PageIndex{10}\): Using a Linear Function to Determine the number of Songs in a Music Collection

Marcus actualmente tiene 200 canciones en su colección de música. Cada mes, agrega 15 canciones nuevas. Escribir una fórmula para el número de canciones,\(N\), en su colección en función del tiempo,\(t\), el número de meses. ¿Cuántas canciones tendrá en un año?

Solución

El valor inicial para esta función es 200 porque actualmente posee 200 canciones, entonces\(N(0)=200\), lo que significa que\(b=200\).

El número de canciones aumenta en 15 canciones al mes, por lo que la tasa de cambio es de 15 canciones al mes. Por lo tanto, eso lo sabemos\(m=15\). Podemos sustituir el valor inicial y la tasa de cambio por la forma pendiente-intercepción de una línea.

Figura\(\PageIndex{13}\)

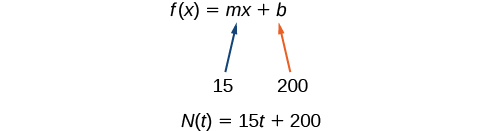
Podemos escribir la fórmula\(N(t)=15t+200\).

Con esta fórmula, podemos entonces predecir cuántas canciones tendrá Marcus en 1 año (12 meses). En otras palabras, podemos evaluar la función en\(t=12\).

\[\begin{align*} N(12)&=15(12)+200 \\ &=180+200 \\ &= 380 \end{align*}\]

Marcus tendrá 380 canciones en 12 meses.

Análisis

Observe que\(N\) es una función lineal creciente. A medida que aumenta la entrada (el número de meses), la salida (número de canciones) aumenta también.

Ejemplo\(\PageIndex{11}\): Using a Linear Function to Calculate Salary Plus Commission

Al trabajar como vendedor de seguros, Ilya gana un salario base más una comisión por cada nueva póliza. Por lo tanto, el ingreso semanal de Ilya, yo, depende del número de pólizas nuevas\(n\),, vende durante la semana. La semana pasada vendió 3 nuevas pólizas, y ganó 760 dólares por semana. La semana anterior, vendió 5 nuevas pólizas y ganó $920. Encontrar una ecuación para\(I(n)\), e interpretar el significado de los componentes de la ecuación.

Solución

La información dada nos da dos pares entrada-salida:\((3,760)\) y\((5,920)\). Comenzamos por encontrar la tasa de cambio.

\[\begin{align*} m&=\dfrac{920-760}{5-3} \\ &=\dfrac{$160}{2 \text{ policies}} \\ &=$80 \text{ per policy} \end{align*}\]

Hacer un seguimiento de las unidades puede ayudarnos a interpretar esta cantidad. Los ingresos aumentaron 160 dólares cuando el número de pólizas aumentó en 2, por lo que la tasa de cambio es de 80 dólares por póliza. Por lo tanto, Ilya gana una comisión de 80 dólares por cada póliza vendida durante la semana.

Entonces podemos resolver por el valor inicial.

\[\begin{align*} I(n)&=80n+b \\ 760&=80(3)+b \text{ when } n=3, I(3)=760 \\ 760-80(3)&=b \\ 520 & =b \end{align*}\]

El valor de\(b\) es el valor inicial de la función y representa los ingresos de Ilya cuando\(n=0\), o cuando no se venden nuevas pólizas. Podemos interpretar esto como el salario base de Ilya para la semana, que no depende del número de pólizas vendidas.

Ahora podemos escribir la ecuación final.

\[I(n)=80n+520 \nonumber\]

Nuestra interpretación final es que el salario base de Ilya es de 520 dólares semanales y gana una comisión adicional de 80 dólares por cada póliza vendida.

Ejemplo de\(\PageIndex{12}\): Using Tabular Form to Write an ecuación para una función lineal

El cuadro\(\PageIndex{1}\) relaciona el número de ratas en una población con el tiempo, en semanas. Usa la tabla para escribir una ecuación lineal.

Mesa\(\PageIndex{1}\)

w, número de semanas	0	2	4	6
P (w), número de ratas	1000	1080	1160	1240

Solución

Podemos ver en la tabla que el valor inicial para el número de ratas es de 1000, entonces\(b=1000\).

En lugar de resolver para\(m\), podemos decir al mirar la tabla que la población aumenta en 80 por cada 2 semanas que pasan. Esto significa que la tasa de cambio es de 80 ratas por 2 semanas, lo que puede simplificarse a 40 ratas por semana.

\[P(w)=40w+1000 \nonumber\]

Si no nos percatamos de la tasa de cambio de la tabla aún podríamos resolver para la pendiente usando dos puntos cualesquiera de la tabla. Por ejemplo, usando\((2,1080)\) y\((6,1240)\)

\[\begin{align*} m&=\dfrac{1240-1080}{6-2} \\ &=\dfrac{160}{4} \\ &= 40\end{align*}\]

¿El valor inicial siempre se proporciona en una tabla de valores como Table\(\PageIndex{1}\)?

No. A veces el valor inicial se proporciona en una tabla de valores, pero a veces no lo es. Si ves una entrada de 0, entonces el valor inicial sería la salida correspondiente. Si no se proporciona el valor inicial porque no hay ningún valor de entrada en la tabla igual a 0, busque la pendiente, sustituya un par de coordenadas y la pendiente en\(f(x)=mx+b\), y resuelva para\(b\).

\(\PageIndex{5}\): Se introdujo un nuevo alimento vegetal a un árbol joven para probar su efecto en la altura del árbol. \(\PageIndex{2}\)La tabla muestra la altura del árbol, en pies,\(x\) meses desde que comenzaron las mediciones. Escribir una función lineal,\(H(x)\), donde\(x\) está el número de meses desde el inicio del experimento.

Mesa\(\PageIndex{2}\)

\(x\)	0	2	4	8	12
\(H(x)\)	12.5	13.5	14.5	16.5	18.5

Solución

\(H(x)=0.5x+12.5\)

Ecuaciones Clave

• forma pendiente-intercepción de una línea:\(f(x)=mx+b\)
• pendiente:\(m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{{\Delta}y}{{\Delta}x}=\dfrac{y_2-y_1}{x_2-x_1}\)
• forma de punto-pendiente de una línea:\(y−y_1 =m(x-x_1)\)

Conceptos clave

• Los pares ordenados dados por una función lineal representan puntos en una línea.
• Las funciones lineales se pueden representar en palabras, notación de funciones, forma tabular y forma gráfica.
• La tasa de cambio de una función lineal también se conoce como pendiente.
• Una ecuación en la forma pendiente-intercepción de una línea incluye la pendiente y el valor inicial de la función.
• El valor inicial, o intercepción y, es el valor de salida cuando la entrada de una función lineal es cero. Es el valor y del punto en el que la línea cruza el eje y.
• Una función lineal creciente da como resultado una gráfica que se incline hacia arriba de izquierda a derecha y tiene una pendiente positiva.
• Una función lineal decreciente da como resultado una gráfica que se incline hacia abajo de izquierda a derecha y tiene una pendiente negativa.
• Una función lineal constante da como resultado una gráfica que es una línea horizontal.
• Analizar la pendiente en el contexto de un problema indica si una función lineal es creciente, decreciente o constante.
• La pendiente de una función lineal se puede calcular dividiendo la diferencia entre los valores y por la diferencia en los valores x correspondientes de dos puntos cualesquiera de la línea.
• La pendiente y el valor inicial se pueden determinar dada una gráfica o dos puntos cualesquiera en la línea.
• Un tipo de notación de función es la forma pendiente-intercepción de una ecuación.
• La forma punto-pendiente es útil para encontrar una ecuación lineal cuando se le da la pendiente de una línea y un punto.
• La forma punto-pendiente también es conveniente para encontrar una ecuación lineal cuando se le dan dos puntos a través de los cuales pasa una línea.
• La ecuación para una función lineal se puede escribir si se\(b\) conocen la pendiente\(m\) y el valor inicial.
• Una función lineal se puede utilizar para resolver problemas del mundo real.
• Una función lineal se puede escribir a partir de forma tabular.

Notas al pie

1 www.chinahighlights.com/shang... glev-train.htm
2 www.cbsnews.com/8301-501465_1... ay-study-says/

Glosario

función lineal decreciente

una función con pendiente negativa: Si\(f(x)=mx+b\), entonces\(m<0\).

aumentar la función lineal

una función con una pendiente positiva: Si\(f(x)=mx+b\), entonces\(m>0\).

función lineal

una función con una tasa de cambio constante que es un polinomio de grado 1, y cuya gráfica es una línea recta

forma de punto-pendiente

la ecuación para una línea que representa una función lineal de la forma\ (y−y_1=m (x−x_1)

pendiente

la relación entre el cambio en los valores de salida y el cambio en los valores de entrada; una medida de la inclinación de una línea

forma pendiente-intercepción

la ecuación para una línea que representa una función lineal en la forma\(f(x)=mx+b\)

Intercepción en Y

el valor de una función cuando el valor de entrada es cero; también conocido como valor inicial