8.5: Rotación de Ejes

Objetivos de aprendizaje

• Identificar secciones cónicas no degeneradas dadas sus ecuaciones de forma general.
• Utilice fórmulas de rotación de ejes.
• Escribir ecuaciones de cónicas rotadas en forma estándar.
• Identificar cónicas sin ejes giratorios.

Como hemos visto, se forman secciones cónicas cuando un plano se cruza con dos conos circulares rectos alineados punta a punta y que se extienden infinitamente lejos en direcciones opuestas, que también llamamos cono. La forma en que cortamos el cono determinará el tipo de sección cónica formada en la intersección. Se forma un círculo cortando un cono con un plano perpendicular al eje de simetría del cono. Una elipse se forma cortando un solo cono con un plano inclinado no perpendicular al eje de simetría. Una parábola se forma cortando el plano a través de la parte superior o inferior del doble cono, mientras que se forma una hipérbola cuando el plano corta tanto la parte superior como la inferior del cono (Figura\(\PageIndex{1}\)).

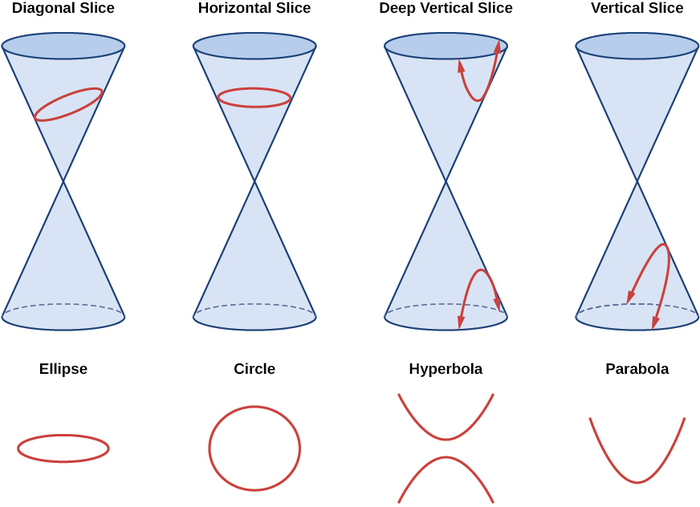
Figura\(\PageIndex{1}\): Las secciones cónicas no degeneradas

Elipses, círculos, hipérbolas y parábolas a veces se denominan secciones cónicas no degeneradas, en contraste con las secciones cónicas degeneradas, que se muestran en la Figura\(\PageIndex{2}\). Una cónica degenerada resulta cuando un plano cruza el doble cono y pasa a través del ápice. Dependiendo del ángulo del plano, son posibles tres tipos de secciones cónicas degeneradas: un punto, una línea o dos líneas de intersección.

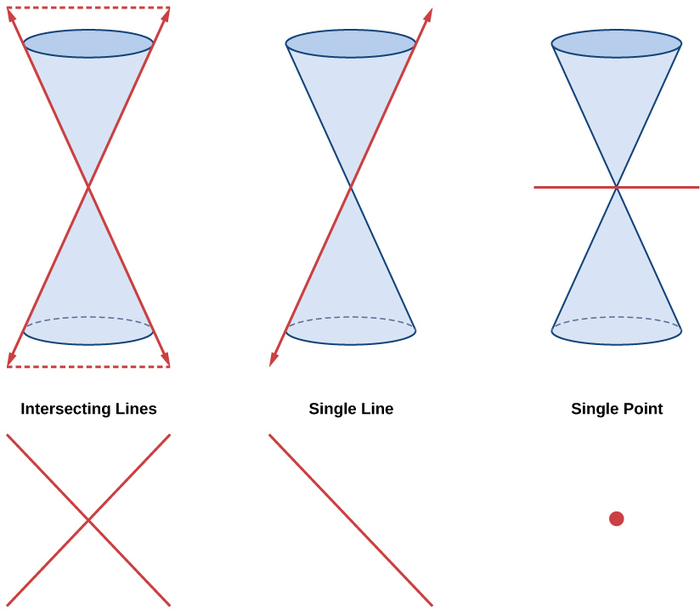
Figura\(\PageIndex{2}\): Secciones cónicas degeneradas

Identificación de cónicas no degeneradas en forma general

En secciones anteriores de este capítulo, nos hemos centrado en las ecuaciones de forma estándar para secciones cónicas no degeneradas. En esta sección, desplazaremos nuestro enfoque hacia la ecuación de forma general, que puede ser utilizada para cualquier cónica. La forma general se establece igual a cero, y los términos y coeficientes se dan en un orden particular, como se muestra a continuación.

\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\)

donde\(A\),\(B\), y no\(C\) son todos cero. Podemos usar los valores de los coeficientes para identificar qué tipo cónico está representado por una ecuación dada.

Podrán notar que la ecuación de forma general tiene un\(xy\) término que no hemos visto en ninguna de las ecuaciones de forma estándar. Como discutiremos más adelante, el\(xy\) término gira la cónica siempre que no\(B\) sea igual a cero.

Mesa\(\PageIndex{1}\)

Secciones Cónicas	Ejemplo
elipse	\(4x^2+9y^2=1\)
círculo	\(4x^2+4y^2=1\)
hipérbola	\(4x^2−9y^2=1\)
parábola	\(4x^2=9y\)o\(4y^2=9x\)
una línea	\(4x+9y=1\)
líneas que se cruzan	\((x−4)(y+4)=0\)
líneas paralelas	\((x−4)(x−9)=0\)
un punto	\(4x^2+4y^2=0\)
sin gráfico	\(4x^2+4y^2=−1\)

FORMA GENERAL DE SECCIONES CÓNICAS

Una sección cónica tiene la forma general

\[Ax^2+Bxy+Cy^2+Dx+Ey+F=0 \label{gen}\]

donde\(A\),\(B\), y no\(C\) son todos cero. Tabla\(\PageIndex{2}\) resume las diferentes secciones cónicas donde\(B=0\), y\(A\) y\(C\) son números reales distintos de cero. Esto indica que la cónica no se ha girado.

Mesa\(\PageIndex{2}\)

elipse	\(Ax^2+Cy^2+Dx+Ey+F=0\),\(A≠C\) y\(AC>0\)
círculo	\(Ax^2+Cy^2+Dx+Ey+F=0\),\(A=C\)
hipérbola	\(Ax^2−Cy^2+Dx+Ey+F=0\)o\(−Ax^2+Cy^2+Dx+Ey+F=0\), donde\(A\) y\(C\) son positivos
parábola	\(Ax^2+Dx+Ey+F=0\)o\(Cy^2+Dx+Ey+F=0\)

Cómo: Dada la ecuación de una cónica, identificar el tipo de cónica

1. Reescribir la ecuación en la forma general (Ecuación\ ref {gen}),\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\)
2. Identificar los valores de\(A\) y\(C\) a partir de la forma general.
   • Si\(A\) y\(C\) son distintos de cero, tienen el mismo signo, y no son iguales entre sí, entonces la gráfica puede ser una elipse.
   • Si\(A\) y\(C\) son iguales y distintos de cero y tienen el mismo signo, entonces la gráfica puede ser un círculo.
   • Si\(A\) y\(C\) son distintos de cero y tienen signos opuestos, entonces la gráfica puede ser una hipérbola.
   • Si cualquiera\(A\) o\(C\) es cero, entonces la gráfica puede ser una parábola.

Si\(B=0\), la sección cónica tendrá ejes verticales y/u horizontales. Si\(B\) no es igual a 0, como se muestra a continuación, se gira la sección cónica. Observe la frase “puede ser” en las definiciones. Esto se debe a que la ecuación puede no representar una sección cónica en absoluto, dependiendo de los valores de\(A\)\(B\),\(C\),\(D\),\(E\), y\(F\). Por ejemplo, el caso degenerado de un círculo o una elipse es un punto:

\[Ax^2+By^2=0,\]

cuando\(A\) y\(B\) tener el mismo signo.

El caso degenerado de una hipérbola es de dos líneas rectas que se cruzan:\(Ax^2+By^2=0\), cuándo\(A\) y\(B\) tienen signos opuestos.

Por otro lado, la ecuación\(Ax^2+By^2+1=0\), cuando\(A\) y\(B\) son positivos no representa en absoluto una gráfica, ya que no hay pares ordenados reales que la satisfagan.

Ejemplo\(\PageIndex{1}\): Identifying a Conic from Its General Form

Identificar la gráfica de cada una de las siguientes secciones cónicas no degeneradas.

1. \(4x^2−9y^2+36x+36y−125=0\)
2. \(9y^2+16x+36y−10=0\)
3. \(3x^2+3y^2−2x−6y−4=0\)
4. \(−25x^2−4y^2+100x+16y+20=0\)

Solución

1. Reescribiendo la forma general (Ecuación\ ref {gen}), tenemos\[\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] 4 x ^ { 2 } + 0 x y + ( - 9 ) y ^ { 2 } + 36 x + 36 y + ( - 125 ) &= 0 \end{align*}\] con\(A=4\) y\(C=−9\), así observamos eso\(A\) y\(C\) tenemos signos opuestos. La gráfica de esta ecuación es una hipérbola.
2. Reescribiendo la forma general (Ecuación\ ref {gen}), tenemos\[\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] 0 x ^ { 2 } + 0 x y + 9 y ^ { 2 } + 16 x + 36 y + ( - 10 ) &= 0 \end{align*}\] con\(A=0\) y\(C=9\). Podemos determinar que la ecuación es una parábola, ya que\(A\) es cero.
3. Reescribiendo la forma general (Ecuación\ ref {gen}), tenemos\[\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] 3 x ^ { 2 } + 0 x y + 3 y ^ { 2 } + ( - 2 ) x + ( - 6 ) y + ( - 4 ) &= 0 \end{align*}\] con\(A=3\) y\(C=3\). Porque\(A=C\), la gráfica de esta ecuación es un círculo.
4. Reescribiendo la forma general (Ecuación\ ref {gen}), tenemos\[\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] ( - 25 ) x ^ { 2 } + 0 x y + ( - 4 ) y ^ { 2 } + 100 x + 16 y + 20 &= 0 \end{align*}\] con\(A=−25\) y\(C=−4\). Porque\(AC>0\) y\(A≠C\), la gráfica de esta ecuación es una elipse.

Ejercicio\(\PageIndex{1}\)

Identificar la gráfica de cada una de las siguientes secciones cónicas no degeneradas.

1. \(16y^2−x^2+x−4y−9=0\)
2. \(16x^2+4y^2+16x+49y−81=0\)

Contestar a

hipérbola

Respuesta b

elipse

Encontrar una nueva representación de la ecuación dada después de rotar a través de un ángulo dado

Hasta ahora, hemos mirado ecuaciones de secciones cónicas sin\(xy\) término, que alinea las gráficas con los ejes x - e y. Cuando agregamos un\(xy\) término, estamos rotando la cónica sobre el origen. Si los ejes x e y se rotan a través de un ángulo\(\theta\), digamos, entonces cada punto del plano puede pensarse que tiene dos representaciones:\((x,y)\) en el plano cartesiano con el eje x y el eje y originales, y\((x^\prime ,y^\prime )\) en el nuevo plano definido por los nuevos ejes girados, llamados eje x' y eje y' (Figura\(\PageIndex{3}\)).

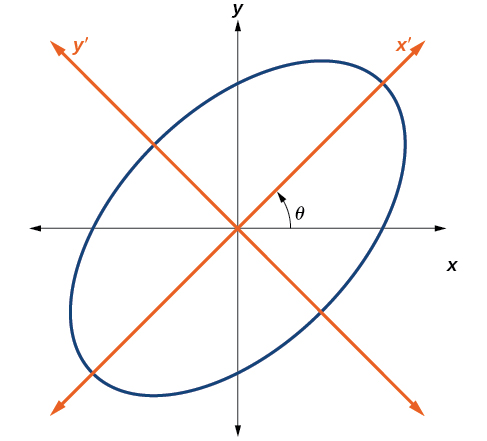
Figura\(\PageIndex{3}\): La gráfica de la elipse girada\(x^2+y^2–xy–15=0\)

Encontraremos las relaciones entre\(x\) y\(y\) en el plano cartesiano con\(x^\prime \) y\(y^\prime \) sobre el nuevo plano girado (Figura\(\PageIndex{4}\)).

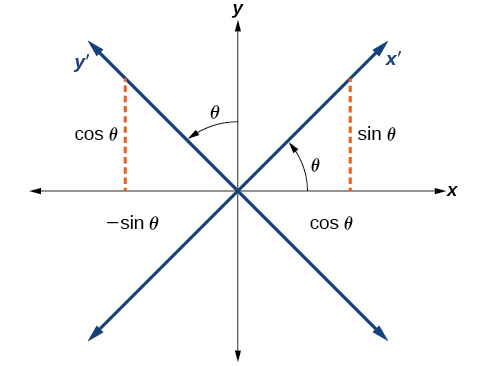
Figura\(\PageIndex{4}\): El plano cartesiano con\(x\) -y\(y\) -ejes y los\(x^\prime\) resultantes− y\(y^\prime\) −ejes formados por una rotación por un ángulo\(\theta\).

Las coordenadas originales x - e y -ejes tienen vectores unitarios\(\hat{i}\) y\(\hat{j}\). Los ejes de coordenadas giradas tienen vectores unitarios\(\hat{i}^\prime\) y\(\hat{j}^\prime\) .El ángulo\(\theta\) se conoce como el ángulo de rotación (Figura\(\PageIndex{5}\)). Podemos escribir los nuevos vectores unitarios en términos de los originales.

\[\hat{i}′=\cos \theta \hat{i}+\sin \theta \hat{j}\]

\[\hat{j}′=−\sin \theta \hat{i}+\cos \theta \hat{j}\]

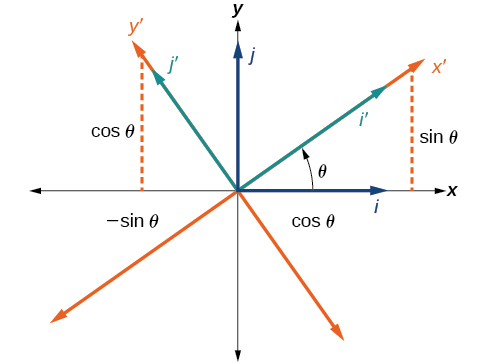
Figura\(\PageIndex{5}\): Relación entre los planos de coordenadas antiguo y nuevo.

Considere un vector\(\vec{u}\) en el nuevo plano de coordenadas. Se puede representar en términos de sus ejes de coordenadas.

\[\begin{align*} \vec{u}&=x^\prime i′+y^\prime j′ \\[4pt] &=x^\prime (i \cos \theta+j \sin \theta)+y^\prime (−i \sin \theta+j \cos \theta) & \text{Substitute.} \\[4pt] &=ix' \cos \theta+jx' \sin \theta−iy' \sin \theta+jy' \cos \theta & \text{Distribute.} \\[4pt] &=ix' \cos \theta−iy' \sin \theta+jx' \sin \theta+jy' \cos \theta & \text{Apply commutative property.} \\[4pt] &=(x' \cos \theta−y' \sin \theta)i+(x' \sin \theta+y' \cos \theta)j & \text{Factor by grouping.} \end{align*}\]

Porque\(\vec{u}=x^\prime i′+y^\prime j′\), tenemos representaciones de\(x\) y\(y\) en términos del nuevo sistema de coordenadas.

\(x=x^\prime \cos \theta−y^\prime \sin \theta\)

y

\(y=x^\prime \sin \theta+y^\prime \cos \theta\)

ECUACIONES DE ROTACIÓN

Si un punto\((x,y)\) en el plano cartesiano se representa en un nuevo plano de coordenadas donde los ejes de rotación se forman girando un ángulo\(\theta\) desde el eje x positivo, entonces las coordenadas del punto con respecto a los nuevos ejes son\((x^\prime ,y^\prime )\). Podemos utilizar las siguientes ecuaciones de rotación para definir la relación entre\((x,y)\) y\((x^\prime , y^\prime )\):

\[x=x^\prime \cos \theta−y^\prime \sin \theta\]

y

\[y=x^\prime \sin \theta+y^\prime \cos \theta\]

Cómo: Dada la ecuación de una cónica, encontrar una nueva representación después de rotar a través de un ángulo

1. Encontrar\(x\) y\(y\) dónde\(x=x^\prime \cos \theta−y^\prime \sin \theta\) y\(y=x^\prime \sin \theta+y^\prime \cos \theta\).
2. Sustituya la expresión por\(x\) y\(y\) en en la ecuación dada, luego simplifique.
3. Escribe las ecuaciones con\(x^\prime \) y\(y^\prime \) en forma estándar.

Ejemplo\(\PageIndex{2}\): Finding a New Representation of an Equation after Rotating through a Given Angle

Encuentra una nueva representación de la ecuación\(2x^2−xy+2y^2−30=0\) después de rotar a través de un ángulo de\(\theta=45°\).

Solución

Encontrar\(x\) y\(y\), dónde\(x=x^\prime \cos \theta−y^\prime \sin \theta\) y\(y=x^\prime \sin \theta+y^\prime \cos \theta\).

Porque\(\theta=45°\),

\[\begin{align*} x &= x^\prime \cos(45°)−y^\prime \sin(45°) \\[4pt] x &= x^\prime \left(\dfrac{1}{\sqrt{2}}\right)−y^\prime \left(\dfrac{1}{\sqrt{2}}\right) \\[4pt] x &=\dfrac{x^\prime −y^\prime }{\sqrt{2}} \end{align*}\]

y

\[\begin{align*} y &= x^\prime \sin(45°)+y^\prime \cos(45°) \\[4pt] y &= x^\prime \left(\dfrac{1}{\sqrt{2}}\right) + y^\prime \left(\dfrac{1}{\sqrt{2}}\right) \\[4pt] y &= \dfrac{x^\prime +y^\prime }{\sqrt{2}} \end{align*}\]

Sustituto\(x=x^\prime \cos\theta−y^\prime \sin\theta\) y\(y=x^\prime \sin \theta+y^\prime \cos \theta\) en\(2x^2−xy+2y^2−30=0\).

\(2{\left(\dfrac{x^\prime −y^\prime }{\sqrt{2}}\right)}^2−\left(\dfrac{x^\prime −y^\prime }{\sqrt{2}}\right)\left(\dfrac{x^\prime +y^\prime }{\sqrt{2}}\right)+2{\left(\dfrac{x^\prime +y^\prime }{\sqrt{2}}\right)}^2−30=0\)

Simplificar.

\(\begin{array}{rl} 2\dfrac{(x^\prime−y^\prime )(x^\prime −y^\prime )}{2}−\dfrac{(x^\prime −y^\prime )(x^\prime +y^\prime )}{2}+2\dfrac{(x^\prime +y^\prime )(x^\prime +y^\prime )}{2}−30=0 & \text{FOIL method} \\[4pt] {x^\prime }^2−2x^\prime y^\prime +{y^\prime }^2−\dfrac{({x^\prime }^2−{y^\prime }^2)}{2}+{x^\prime }^2+2x^\prime y^\prime +{y^\prime }^2−30=0 & \text{Combine like terms.} \\[4pt] 2{x^\prime }^2+2{y^\prime }^2−\dfrac{({x^\prime }^2−{y^\prime }^2)}{2}=30 & \text{Combine like terms.} \\[4pt] 2(2{x^\prime }^2+2{y^\prime }^2−\dfrac{({x^\prime }^2−{y^\prime }^2)}{2})=2(30) & \text{Multiply both sides by 2.} \\[4pt] 4{x^\prime }^2+4{y^\prime }^2−({x^\prime }^2−{y^\prime }^2)=60 & \text{Simplify. } \\[4pt] 4{x^\prime }^2+4{y^\prime }^2−{x^\prime }^2+{y^\prime }2=60 & \text{Distribute.} \\[4pt] \dfrac{3{x^\prime }^2}{60}+\dfrac{5{y^\prime }^2}{60}=\dfrac{60}{60} & \text{Set equal to 1.} \end{array} \)

Escribe las ecuaciones con\(x^\prime \) y\(y^\prime \) en la forma estándar.

\[\dfrac{{x^\prime }^2}{20}+\dfrac{{y^\prime}^2}{12}=1 \nonumber\]

Esta ecuación es una elipse. En la figura se\(\PageIndex{6}\) muestra la gráfica.

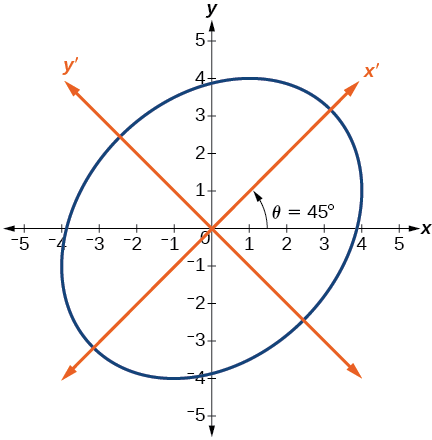
Figura\(\PageIndex{6}\)

Escritura de ecuaciones de cónicas giradas en forma estándar

Ahora que podemos encontrar la forma estándar de una cónica cuando se nos da un ángulo de rotación, aprenderemos a transformar la ecuación de una cónica dada en la forma\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) en forma estándar girando los ejes. Para ello, reescribiremos la forma general como una ecuación en el sistema de\(y^\prime \) coordenadas\(x^\prime \) y sin el\(x^\prime y^\prime \) término, rotando los ejes por una medida de\(\theta\) que satisfaga

\[\cot(2\theta)=\dfrac{A−C}{B}\]

Ya hemos aprendido que cualquier cónica puede estar representada por la ecuación de segundo grado

\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\)

donde\(A\),\(B\), y no\(C\) son todos cero. No obstante\(B≠0\), si, entonces tenemos un\(xy\) término que nos impide reescribir la ecuación en forma estándar. Para eliminarlo, podemos rotar los ejes por un ángulo agudo\(\theta\) donde\(\cot(2\theta)=\dfrac{A−C}{B}\).

• Si\(\cot(2\theta)>0\), entonces\(2\theta\) está en el primer cuadrante, y\(\theta\) está entre\((0°,45°)\).
• Si\(\cot(2\theta)<0\), entonces\(2\theta\) está en el segundo cuadrante, y\(\theta\) está entre\((45°,90°)\).
• Si\(A=C\), entonces\(\theta=45°\).

Cómo: Dada una ecuación para una cónica en\(x^\prime y^\prime \) system, rewrite the equation without the \(x^\prime y^\prime \) term in terms of \(x^\prime \) and \(y^\prime \),where the \(x^\prime \) and \(y^\prime \) axes are rotations of the standard axes by \(\theta\) degrees

1. Encuentra\(\cot(2\theta)\).
2. Encontrar\(\sin \theta\) y\(\cos \theta\).
3. Sustituir\(\sin \theta\) y\(\cos \theta\) en\(x=x^\prime \cos \theta−y^\prime \sin \theta\) y\(y=x^\prime \sin \theta+y^\prime \cos \theta\).
4. Sustituir la expresión por\(x\) y\(y\) en en la ecuación dada, y luego simplificar.
5. Escribe las ecuaciones con\(x^\prime \) y\(y^\prime \) en la forma estándar con respecto a los ejes girados.

Ejemplo\(\PageIndex{3}\): Rewriting an Equation with respect to the \(x^\prime\) and \(y^\prime\) axes without the \(x^\prime y^\prime\) Term

Reescribir la ecuación\(8x^2−12xy+17y^2=20\) en el\(x^\prime y^\prime \) sistema sin\(x^\prime y^\prime \) término.

Solución

Primero, nos encontramos\(\cot(2\theta)\).

\(8x^2−12xy+17y^2=20\rightarrow A=8\),\(B=−12\) y\(C=17\)

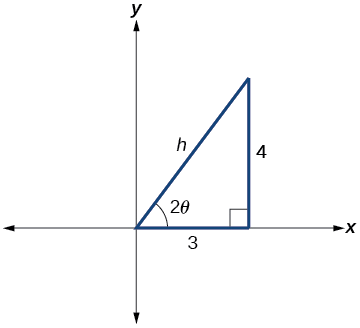
Figura\(\PageIndex{7}\)

De la Figura\(\PageIndex{7}\):

\[ \begin{align*} \cot(2\theta) &=\dfrac{A−C}{B}=\dfrac{8−17}{−12} \\[4pt] & =\dfrac{−9}{−12}=\dfrac{3}{4} \end{align*}\]

\(\cot(2\theta)=\dfrac{3}{4}=\dfrac{\text{adjacent}}{\text{opposite}}\)

Entonces la hipotenusa es

\[ \begin{align*} 3^2+4^2 &=h^2 \\[4pt] 9+16 &=h^2 \\[4pt] 25&=h^2 \\[4pt] h&=5 \end{align*}\]

A continuación, encontramos\(\sin \theta\) y\(\cos \theta\).

\[ \begin{align*} \sin \theta &=\sqrt{\dfrac{1−\cos(2\theta)}{2}}=\sqrt{\dfrac{1−\dfrac{3}{5}}{2}}=\sqrt{\dfrac{\dfrac{5}{5}−\dfrac{3}{5}}{2}}=\sqrt{\dfrac{5−3}{5}⋅\dfrac{1}{2}}=\sqrt{\dfrac{2}{10}}=\sqrt{\dfrac{1}{5}} \\ \sin \theta &= \dfrac{1}{\sqrt{5}} \\ \cos \theta &= \sqrt{\dfrac{1+\cos(2\theta)}{2}}=\sqrt{\dfrac{1+\dfrac{3}{5}}{2}}=\sqrt{\dfrac{\dfrac{5}{5}+\dfrac{3}{5}}{2}}=\sqrt{\dfrac{5+3}{5}⋅\dfrac{1}{2}}=\sqrt{\dfrac{8}{10}}=\sqrt{\dfrac{4}{5}} \\ \cos \theta &= \dfrac{2}{\sqrt{5}} \end{align*}\]

Sustituir los valores de\(\sin \theta\) y\(\cos \theta\) en\(x=x^\prime \cos \theta−y^\prime \sin \theta\) y\(y=x^\prime \sin \theta+y^\prime \cos \theta\).

\[ \begin{align*} x &=x'\cos \theta−y^\prime \sin \theta \\[4pt] &=x^\prime \left(\dfrac{2}{\sqrt{5}}\right)−y^\prime \left(\dfrac{1}{\sqrt{5}}\right) \\[4pt] &=\dfrac{2x^\prime −y^\prime }{\sqrt{5}} \end{align*}\]

y

\[ \begin{align*} y&=x^\prime \sin \theta+y^\prime \cos \theta \\[4pt] &=x^\prime \left(\dfrac{1}{\sqrt{5}}\right)+y^\prime \left(\dfrac{2}{\sqrt{5}}\right) \\[4pt] &=\dfrac{x^\prime +2y^\prime }{\sqrt{5}} \end{align*}\]

Sustituir las expresiones para\(x\) y\(y\) en en la ecuación dada, y luego simplificar.

\[ \begin{align*} 8{\left(\dfrac{2x^\prime −y^\prime }{\sqrt{5}}\right)}^2−12\left(\dfrac{2x^\prime −y^\prime }{\sqrt{5}}\right)\left(\dfrac{x^\prime +2y^\prime }{\sqrt{5}}\right)+17{\left(\dfrac{x^\prime +2y^\prime }{\sqrt{5}}\right)}^2&=20 \\[4pt] 8\left(\dfrac{(2x^\prime −y^\prime )(2x^\prime −y^\prime )}{5}\right)−12\left(\dfrac{(2x^\prime −y^\prime )(x^\prime +2y^\prime )}{5}\right)+17\left(\dfrac{(x^\prime +2y^\prime )(x^\prime +2y^\prime )}{5}\right)&=20 \\[4pt] 8(4{x^\prime }^2−4x^\prime y^\prime +{y^\prime }^2)−12(2{x^\prime }^2+3x^\prime y^\prime −2{y^\prime }^2)+17({x^\prime }^2+4x^\prime y^\prime +4{y^\prime }^2)&=100 \\[4pt] 32{x^\prime }^2−32x^\prime y^\prime +8{y^\prime }^2−24{x^\prime }^2−36x^\prime y^\prime +24{y^\prime }^2+17{x^\prime }^2+68x^\prime y^\prime +68{y^\prime }^2&=100 \\[4pt] 25{x^\prime }^2+100{y^\prime }^2&=100 \\[4pt] \dfrac{25}{100}{x^\prime }^2+\dfrac{100}{100}{y^\prime }^2&=\dfrac{100}{100} \end{align*}\]

Escribir las ecuaciones con\(x^\prime \) y\(y^\prime \) en la forma estándar con respecto al nuevo sistema de coordenadas.

\[\dfrac{{x^\prime }^2}{4}+\dfrac{{y^\prime }^2}{1}=1 \nonumber\]

En la figura se\(\PageIndex{8}\) muestra la gráfica de la elipse.

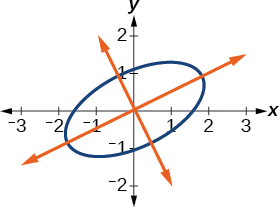
Figura\(\PageIndex{8}\)

Ejercicio\(\PageIndex{2}\)

Reescribir el\(13x^2−6\sqrt{3}xy+7y^2=16\) en el\(x^\prime y^\prime \) sistema sin el\(x^\prime y^\prime \) término.

Contestar

\(\dfrac{{x^\prime }^2}{4}+\dfrac{{y^\prime }^2}{1}=1\)

Ejemplo\(\PageIndex{4}\) :Graphing an Equation That Has No \(x^\prime y^\prime \) Terms

Grafique la siguiente ecuación relativa al\(x^\prime y^\prime \) sistema:

\(x^2+12xy−4y^2=30\)

Solución

Primero, nos encontramos\(\cot(2\theta)\).

\(x^2+12xy−4y^2=20\rightarrow A=1\),\(B=12\), y\(C=−4\)

\[\begin{align*} \cot(2\theta) &= \dfrac{A−C}{B} \\ \cot(2\theta) &= \dfrac{1−(−4)}{12} \\ \cot(2\theta) &= \dfrac{5}{12} \end{align*}\]

Porque\(\cot(2\theta)=\dfrac{5}{12}\), podemos dibujar un triángulo de referencia como en la Figura\(\PageIndex{9}\).

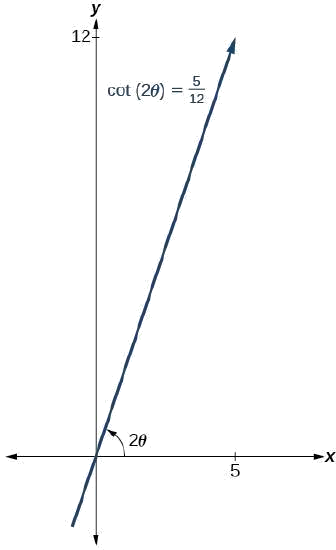
Figura\(\PageIndex{9}\)

\(\cot(2\theta)=\dfrac{5}{12}=\dfrac{adjacent}{opposite}\)

Así, la hipotenusa es

\[ \begin{align*} 5^2+{12}^2&=h^2 \\[4pt] 25+144 &=h^2 \\[4pt] 169 &=h^2 \\[4pt] h&=13 \end{align*}\]

A continuación, encontramos\(\sin \theta\) y\(\cos \theta\). Usaremos identidades de medio ángulo.

\(\sin \theta=\sqrt{\dfrac{1−\cos(2\theta)}{2}}=\sqrt{\dfrac{1−\dfrac{5}{13}}{2}}=\sqrt{\dfrac{\dfrac{13}{13}−\dfrac{5}{13}}{2}}=\sqrt{\dfrac{8}{13}⋅\dfrac{1}{2}}=\dfrac{2}{\sqrt{13}}\)

\(\cos \theta=\sqrt{\dfrac{1+\cos(2\theta)}{2}}=\sqrt{\dfrac{1+\dfrac{5}{13}}{2}}=\sqrt{\dfrac{\dfrac{13}{13}+\dfrac{5}{13}}{2}}=\sqrt{\dfrac{18}{13}⋅\dfrac{1}{2}}=\dfrac{3}{\sqrt{13}}\)

Ahora nos encontramos\(x\) y\(y\).

\(x=x^\prime \cos \theta−y^\prime \sin \theta\)

\(x=x^\prime \left(\dfrac{3}{\sqrt{13}}\right)−y^\prime \left(\dfrac{2}{\sqrt{13}}\right)\)

\(x=\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}\)

y

\(y=x^\prime \sin \theta+y^\prime \cos \theta\)

\(y=x^\prime \left(\dfrac{2}{\sqrt{13}}\right)+y^\prime \left(\dfrac{3}{\sqrt{13}}\right)\)

\(y=\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}\)

Ahora sustituimos\(x=\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}\) y\(y=\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}\) en\(x^2+12xy−4y^2=30\).

\(\begin{array}{rl} {\left(\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}\right)}^2+12\left(\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}\right)\left(\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}\right)−4{\left(\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}\right)}^2=30 \\ \left(\dfrac{1}{13}\right)[ {(3x^\prime −2y^\prime )}^2+12(3x^\prime −2y^\prime )(2x^\prime +3y^\prime )−4{(2x^\prime +3y^\prime )}^2 ]=30 & \text{Factor.} \\ \left(\dfrac{1}{13}\right)[ 9{x^\prime }^2−12x^\prime y^\prime +4{y^\prime }^2+12(6{x^\prime }^2+5x^\prime y^\prime −6{y^\prime }^2)−4(4{x^\prime }^2+12x^\prime y^\prime +9{y^\prime }^2) ]=30 & \text{Multiply.} \\ \left(\dfrac{1}{13}\right)[ 9{x^\prime }^2−12x^\prime y^\prime +4{y^\prime }^2+72{x^\prime }^2+60x^\prime y^\prime −72{y^\prime }^2−16{x^\prime }^2−48x^\prime y^\prime −36{y^\prime }^2 ]=30 & \text{Distribute.} \\ \left(\dfrac{1}{13}\right)[ 65{x^\prime }^2−104{y^\prime }^2 ]=30 & \text{Combine like terms.} \\ 65{x^\prime }^2−104{y^\prime }^2=390 & \text{Multiply.} \\ \dfrac{{x^\prime }^2}{6}−\dfrac{4{y^\prime }^2}{15}=1 & \text{Divide by 390.} \end{array}\)

La figura\(\PageIndex{10}\) muestra la gráfica de la hipérbola\(\dfrac{{x^\prime }^2}{6}−\dfrac{4{y^\prime }^2}{15}=1\)

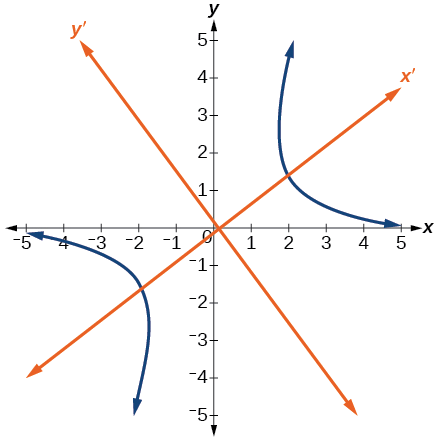
Figura\(\PageIndex{10}\)

Identificación de Cónicas sin Ejes Giratorios

Ahora hemos llegado al círculo completo. ¿Cómo identificamos el tipo de cónica descrita por una ecuación? ¿Qué sucede cuando se rotan los ejes? Recordemos, la forma general de una cónica es

\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\)

Si aplicamos las fórmulas de rotación a esta ecuación obtenemos la forma

\(A′{x^\prime }^2+B′x^\prime y^\prime +C′{y^\prime }^2+D′x^\prime +E′y^\prime +F′=0\)

Se puede demostrar que

\(B^2−4AC={B′}^2−4A′C′\)

La expresión no varía después de la rotación, por lo que llamamos a la expresión invariante. El discriminante,\(B^2−4AC\), es invariante y permanece sin cambios después de la rotación. Debido a que el discriminante permanece inalterado, observar al discriminante nos permite identificar la sección cónica.

CÓMO: USAR EL DISCRIMINANTE PARA IDENTIFICAR UN

Si la ecuación

\[Ax^2+Bxy+Cy^2+Dx+Ey+F=0\]

se transforma rotando ejes en la ecuación

\[A′{x^\prime }^2+B′x^\prime y^\prime +C′{y^\prime }^2+D′x^\prime +E′y^\prime +F′=0\]

entonces\[B^2−4AC={B′}^2−4A′C′\]

La ecuación\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) es una elipse, una parábola, o una hipérbola, o un caso degenerado de uno de estos. Si el discriminante,\(B^2−4AC\), es

• \(<0\), la sección cónica es una elipse
• \(=0\), la sección cónica es una parábola
• \(>0\), la sección cónica es una hipérbola

Ejemplo\(\PageIndex{5}\): Identifying the Conic without Rotating Axes

Identificar la cónica para cada una de las siguientes sin ejes giratorios.

1. \(5x^2+2\sqrt{3}xy+2y^2−5=0\)
2. \(5x^2+2\sqrt{3}xy+12y^2−5=0\)

Solución

a. comencemos por determinar\(A\),\(B\), y\(C\).

\(\underbrace{5}_{A}x^2+\underbrace{2\sqrt{3}}_{B}xy+\underbrace{2}_{C}y^2−5=0\)

Ahora, encontramos al discriminante.

\[\begin{align*} B^2−4AC &= {(2\sqrt{3})}^2−4(5)(2) \\ &=4(3)−40 \\ &=12−40 \\ &=−28<0 \end{align*}\]

Por lo tanto,\(5x^2+2\sqrt{3}xy+2y^2−5=0\) representa una elipse.

b. nuevamente, comencemos por determinar\(A\),\(B\), y\(C\).

\(\underbrace{5}_{A}x^2+\underbrace{2\sqrt{3}}_{B}xy+\underbrace{12}_{C}y^2−5=0 \nonumber\)

Ahora, encontramos al discriminante.

\[\begin{align*} B^2−4AC &= {(2\sqrt{3})}^2−4(5)(12) \\ &= 4(3)−240 \\ &= 12−240 \\ &=−228<0 \end{align*}\]

Por lo tanto,\(5x^2+2\sqrt{3}xy+12y^2−5=0\) representa una elipse.

Ejercicio\(\PageIndex{3}\)

Identificar la cónica para cada una de las siguientes sin ejes giratorios.

1. \(x^2−9xy+3y^2−12=0\)
2. \(10x^2−9xy+4y^2−4=0\)

Contestar a

hipérbola

Respuesta b

elipse

Ecuaciones Clave

Ecuación general de forma de una sección cónica	\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\)
Rotación de una sección cónica	\(x=x^\prime \cos \theta−y^\prime \sin \theta\) \(y=x^\prime \sin \theta+y^\prime \cos \theta\)
Ángulo de rotación	\(\theta\), donde\(\cot(2\theta)=\dfrac{A−C}{B}\)

Conceptos clave

• Cuatro formas básicas pueden resultar de la intersección de un plano con un par de conos circulares rectos conectados cola a cola. Incluyen una elipse, un círculo, una hipérbola y una parábola.
• Una sección cónica no degenerada tiene la forma general\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) donde\(A\),\(B\) y no\(C\) son todas cero. Los valores de\(A\),\(B\), y\(C\) determinan el tipo de cónica. Ver Ejemplo\(\PageIndex{1}\).
• Ecuaciones de secciones cónicas con un\(xy\) término se han rotado sobre el origen. Ver Ejemplo\(\PageIndex{2}\).
• La forma general se puede transformar en una ecuación en el sistema de\(y^\prime \) coordenadas\(x^\prime \) y sin el\(x^\prime y^\prime \) término. Ver Ejemplo\(\PageIndex{3}\) y Ejemplo\(\PageIndex{4}\).
• Una expresión se describe como invariante si permanece sin cambios después de rotar. Debido a que el discriminante es invariante, observarlo nos permite identificar la sección cónica. Ver Ejemplo\(\PageIndex{5}\).