1.4: Abstracción. ¿Qué es un grupo?

Última actualización
Guardar como PDF

Page ID: 111004

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Entonces ahora tenemos muchos ejemplos de simetría, pero ¿qué, exactamente es un grupo?

Primero, recordemos de dónde vienen los números. Te imaginas tener un juego de tres piñas, o un juego de tres personas, o un juego de tres botellas. Todos estos comparten la propiedad de 'tres-ness'. Entonces, cuando decimos el número tres, describe todos estos conjuntos diferentes. El número tres es una abstracción de la propiedad de un conjunto que contiene tres cosas.

¿Qué es un grupo? ¡Un grupo es una abstracción de simetría! Así como un número describe todos los conjuntos con un cierto número de cosas en él, un grupo dado describe todos los objetos con cierto tipo de simetría. He aquí un ejemplo: La 'cara muy simétrica' tiene dos simetrías, relacionadas por una reflexión. Asimismo, el polinomio simétrico$f(x,y)=x+y$ tiene dos simetrías, una de dejar$f$ solo, y otra de intercambiar las dos variables$x$ y$y$. Si pensamos en cambiar$x$ y$y$ como reflejo, ¡vemos que la cara y el polinomio de alguna manera tienen el mismo tipo de simetría! El grupo es esa medida de simetría.

Ahora, en ese último ejemplo, los dos objetos tenían el mismo número de simetrías. Resulta que solo contar simetrías no es suficiente para decir si los dos objetos tienen el mismo grupo de simetrías. Piense en las simetrías de nuestro triángulo equilátero: hubo simetrías rotacionales, y hubo una simetría de reflexión. Y había seis simetrías en total. Ahora, considere un hexágono regular con algunas protuberancias colocadas regularmente en cada lado, para que no haya simetría de reflexión disponible. Así, este objeto tiene seis simetrías rotacionales, pero no se puede voltear como el triángulo. Por lo tanto, tiene el mismo número de simetrías que el triángulo equilátero, pero el conjunto de simetrías es de alguna manera diferente.

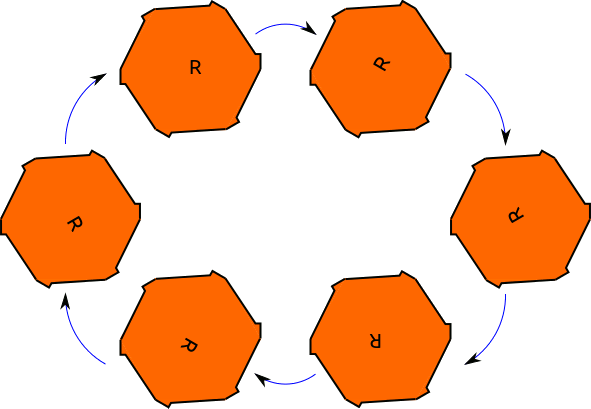
$bumpyHexRotations.gif$

Las seis simetrías rotacionales del hexágono accidentado. La flecha azul representa la rotación$r$;$r^6=id$.

Colaboradores y Atribuciones

Template:ContribDenton