1.6: Topología del Plano Complejo

Barrios

Un\(ε\) barrio, también llamado bola abierta o disco abierto, de un número complejo\(z_{0}\) consiste en todos los puntos que se\(z\) encuentran dentro pero no en un círculo centrado en\(z_{0}\) y con radio\(ε>0\) y es expresado por

\ (\ begin {eqnarray}
B_ {\ varepsilon} (z_0) =\ {z: |z-z_0|\ lt\ varepsilon\}
\ end {eqnarray}\)

El\(ε\) barrio cerrado de\(z_{0}\) se expresa por

\ (\ begin {eqnarray}
\ overline {B} _ {\ varepsilon} (z_0) =\ {z: |z-z_0|\ leq\ varepsilon\}
\ end {eqnarray}\)

Y finalmente, un\(ε\) barrio borrado de\(z_{0}\), también llamado bolas o discos perforados, se expresa por

\ (\ begin {eqnarray}
B_ {\ varepsilon} (z_0)\ setmenos\ {z_0\} =\ {z:0\ lt |z-z_0|\ lt\ varepsilon\}
\ end {eqnarray}\)

La Figura 1 muestra la representación geométrica de los siguientes ejemplos:

1. \(B_{1}(0)=\left \{z:|z|<1\right \}\)
2. \(\bar{B}_{\frac{7}{8}}(-1-\sqrt{2}i)=\left \{ z:\left | z-(-1-\sqrt{2}i) \right |\leq \frac{7}{8} \right \}\)
3. \(\bar{B}_{\frac{1}{2}}(2+\sqrt{3}i)\setminus \left \{ 2+\sqrt{3}i \right \}=\left \{ z:0< \left | z-(2+\sqrt{3}i) \right |\leq \frac{1}{2} \right \}\)

Figura 1: Representación geométrica de barrios.

---

Clasificación de puntos

\(z_{0}\)Se dice que un punto es un punto interior de un conjunto\(S\subset \mathbb{C}\) siempre que haya algún vecindario de\(z_{0}\) que contenga solo puntos de\(S\); se le llama punto exterior de\(S\) cuando existe un vecindario del mismo que no contenga puntos de\(S\). Si no\(z_{0}\) es ninguno de estos, es un punto límite de\(S\). Un punto límite es, por lo tanto, un punto cuyos barrios contienen al menos un punto adentro\(S\) y al menos un punto no adentro\(S\). La totalidad de todos los puntos límite se llama el límite de\(S\).

En este texto usaremos la siguiente notación:

1. Int\(S=\left \{ z:z \,is \,an\,interior\,point\,of \,S \right \}\)
2. Ext\(S=\left \{ z:z \,is \,an\,exterior\,point\,of \,S \right \}\)
3. \(\partial S=\left \{ z:z \,is \,a\,boundary\,point\,of \,S \right \}\)

Figura 2: Interior, contorno y exterior del conjunto S.

Considerando los ejemplos anteriores de barrios, vamos

\(S_{1}=B_{1}(0)\),\(S_{2}=\bar{B}_{\frac{7}{8}}(-1-\sqrt{2}i)\) y\(S_{3}=\bar{B}_{\frac{1}{2}}(2+\sqrt{3}i)\setminus \left \{ 2+\sqrt{3}i \right \}\).

Así, pues\(S_{1}\) tenemos:

• Int\(S_{1}=B_{1}(0)\)
• Ext\(S_{1}=\left \{ z:\left | z \right |> 1 \right \}\)
• \(\partial S_{1}=\left \{ z:\left | z \right |= 1 \right \}\)

Para\(S_{2}\) contamos con:

• Int\(S_{2}=B_{\frac{7}{8}}(-1-\sqrt{2})\)
• Ext\(S_{2}=\left \{ z:\left | z-(-1-\sqrt{2}i) \right |>\frac{7}{8} \right \}\)
• \(\partial S_{2}=\left \{ z:\left | z-(-1-\sqrt{2}i) \right |=\frac{7}{8} \right \}\)

Y por último,\(S_{3}\) pues tenemos:

• Int\( S_{3}=B_{\frac{1}{2}}(2+\sqrt{3})\)
• Ext\(S_{3}=\left \{ z:\left | z-(2+\sqrt{3}i) \right |>\frac{1}{2} \right \}\)
• \(\partial S_{3}=\left \{ z:\left | z-(2+\sqrt{3}i) \right |=\frac{1}{2} \right \}\cup \left \{ 0 \right \}\)

---

Espacio topológico

Un conjunto\(S\) está abierto si por cada\(z\in S\), sale de\(\varepsilon > 0\) tal manera que

\(B_{\varepsilon }(z)\subset S\).

Es decir, el Int\(S=S\). Un conjunto\(S\) se cierra si contiene todos sus puntos de contorno, es decir

\(\partial S\subseteq S\).

El conjunto\(\mathbb{C}\) es tanto abierto como cerrado ya que no tiene puntos límite.

El conjunto\(\mathbb{C}\), junto con la colección,\(\tau =\left \{ S\subseteq \mathbb{C}:S \,is \,open \right \}\) es un espacio topológico, y esto lo expresa la pareja\(\left ( \mathbb{C},\tau  \right )\). El espacio topológico\(\left ( \mathbb{C},\tau  \right )\) satisface lo siguiente:

1. \(\varnothing \)y\(\mathbb{C}\) están abiertos.
2. Siempre que dos o más sets estén abiertos, entonces también lo es su unión.
3. Siempre que los conjuntos\(S_{1}\) y\(S_{2}\) estén abiertos, entonces así es\(S_{1}\cap S_{2}\).

 

Nota: La definición técnica del espacio topológico es un poco poco intuitiva, sobre todo si no se ha estudiado la topología. En esencia, establece que las propiedades geométricas de los subconjuntos de se\(\mathbb{C}\) conservarán cuando se apliquen transformaciones continuas (funciones o mapeos).

El cierre de un conjunto\(S\) es el conjunto cerrado que consiste en todos los puntos\(S\) junto con el límite de\(S\). En otras palabras

\(\bar{S}=S\cup \partial S\).

\(S\)Se conecta un conjunto abierto si cada par de puntos\(z_{1}\) y\(z_{2}\) en él se puede unir mediante una línea poligonal, que consiste en un número finito de segmentos de línea unidos de extremo a extremo, que se encuentra completamente en\(S\).

Figura 3: Conjunto conectado.

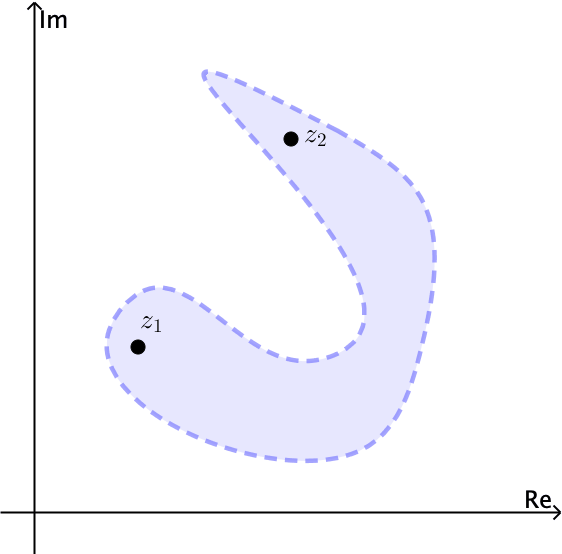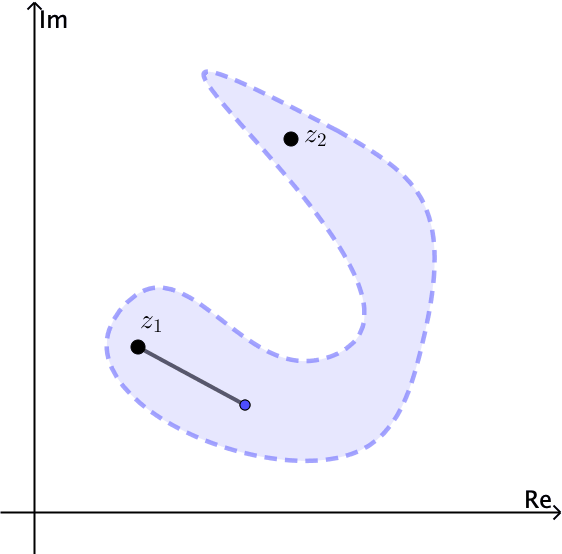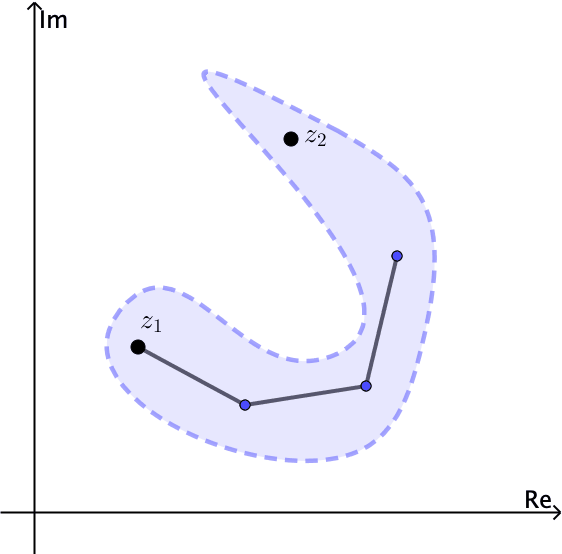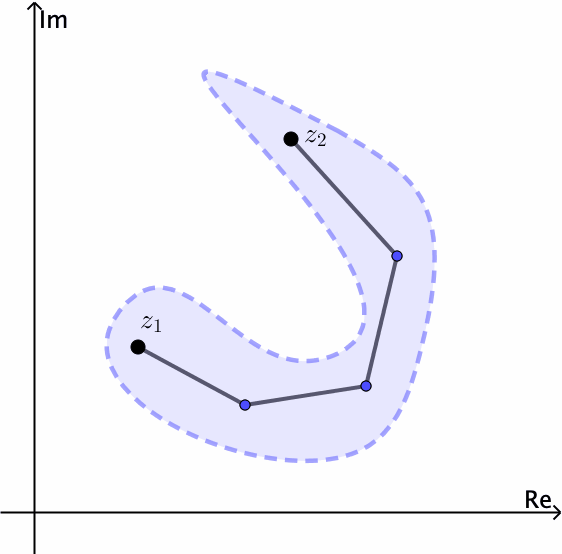
Observe por ejemplo que el conjunto abierto\(\left | z \right |< 1\) está conectado. El anillo\(1< \left | z \right |<2\) está abierto y también conectado, ver Figuras 4 y 5.

Figura 4:\(\left | z \right |< 1\)

Figura 5:\(\left | z \right |<2\)

Un conjunto abierto no vacío que está conectado se llama dominio. En este contexto, cualquier barrio es un dominio. Un dominio junto con algunos, ninguno o todos sus puntos límite se conoce como región. En otras palabras, a un conjunto cuyo interior es un dominio se le llama región. Un conjunto\(S\) está acotado si hay\(R>0\) tal que

\(S\subset B_{R}(0)=\left \{ z\in \mathbb{C}:\left | z \right |<R \right \}\).

Figura 6: Conjunto acotado.

Ejercicio\(\PageIndex{1}\)

Esbozar el conjunto\(S\) de puntos en el plano complejo satisfaciendo la desigualdad dada. Determine si el conjunto es (a) abierto, (b) cerrado, (c) un dominio, (d) acotado, o (e) conectado.

• \(Im(z)<0\)
• \(−1<Re(z)<1\)
• \(|z|>1|z|>1\)
• \(2≤|z−3+4i|≤5\)