2.4: La función logarítmica

 

Considera\(z\) cualquier número complejo distinto de cero. Nos gustaría resolver para\(w\), la ecuación

\ (\ begin {eqnarray}\ label {log1}
e^w=z.
\ end {eqnarray}\)

Si\(Θ=Arg\,(z)\) con\(-\pi < \Theta < \pi \), entonces\(z\) y se\(w\) puede escribir de la siguiente manera

\(z=re^{i\Theta }\)y\(w=u+iv\).

Entonces la ecuación (1) se convierte

\(e^{u}e^{iv}=re^{i\Theta }\).

Por lo tanto, tenemos

\(e^{u}=r\)y\(v=\Theta +2n\pi \)

donde\(n\in \mathbb{Z}\). Dado que\(e^{u}=r\) es lo mismo que\(u=ln\,r\), se deduce que la ecuación (1) se satisface si y solo si\(w\) tiene uno de los valores

\(w=ln\,r+i\left ( \Theta +2n\pi  \right )\,\,\,\left ( n\in \mathbb{Z} \right )\).

Por lo tanto, la función logarítmica (de múltiples valores) de una variable compleja distinta de cero\(z=re^{i\Theta }\) se define por la fórmula

\ begin {eqnarray}\ label {log2}
\ log z=\ ln r +i\ left (\ Theta + 2n\ pi\ derecha)\ quad\ quad (n\ in\ mathbb Z).
\ end {eqnarray}

Ejemplo\(\PageIndex{1}\)

Ejemplo 1: Calcular\(log⁡\,z\) para\(z=-1-\sqrt{3}i\).

Solución: Si\(z=-1-\sqrt{3}i\), entonces\(r=2\) y\(\Theta =-\frac{2\pi }{3}\). De ahí

\(log\,\left ( -1-\sqrt{3}i \right )=ln\,2+i\left ( -\frac{2\pi }{3}+2n\pi  \right )=ln\,2+2\left ( n-\frac{1}{3} \right )\pi i\)

con\(n\in \mathbb{Z}\).

El valor principal de\(log\,z\) es el valor obtenido de la ecuación (2) cuando\(n=0\) y se denota por\(Log\,z\). Así

\(Log\,z=ln\,r+i\Theta \).

La función\(Log\,z\) está bien definida y de un solo valor cuando\(z≠0\) y que

\(log\,z=Log\,z+2n\pi i\,\,\,\left ( n\in \mathbb{Z} \right )\)

Esto se reduce al logaritmo habitual en el cálculo cuando\(z\) es un número real positivo.

Ejemplo\(\PageIndex{2}\)

Ejemplo 2: Calcular\(log\,⁡(1)\) y\(log\,⁡(−1)\).

Solución: De la expresión (2)

\(log\left (1  \right )=ln\,1+i\left ( 0+2n\pi  \right )=2n\pi i\,\,\,\left ( n\in \mathbb{Z} \right )\)

y

\(log\left (-1  \right )=ln\,1+i\left ( \pi +2n\pi  \right )=\left ( 2n+1 \right )\pi i\,\,\,\left ( n\in \mathbb{Z} \right )\)

Observe que\(Log\,(1)=0\) y\(log\,⁡(−1)=\pi i\).

La expresión (2) también es equivalente a lo siguiente:

\ (\ begin {eqnarray*}
\ log z&=&\ ln |z| +i\,\ textbf {arg} (z)\\
&=&\ ln |z| +i\,\ textbf {Arg} (z) +2ni\,\ pi\ quad\ quad (n\ in\ mathbb Z)
\ end {eqnarray*}\)

Algunas propiedades básicas de la función logzlogz son las siguientes:

1. \(\log \left(z_1 \,z_2\right)=\log z_1 + \log  z_2\)
2. \(\log\left( \dfrac{z_1}{z_2}\right)=\log z_1 -\log z_2\)
3. Se puede sostener\(\text{Log}\,\left(z_1 \,z_2\right)\neq \text{Log}\, z_1 + \text{Log}\,  z_2\)

---

Ramas de logaritmos

A partir de la definición (2) let\(\theta = \Theta + 2n\pi  (n\in \mathbb Z)\), así podemos escribir

\ (\ begin {eqnarray}\ label {log30}
\ log z =\ ln r +i\ theta.
\ end {eqnarray}\)

Ahora, dejemos\(\alpha\) ser cualquier número real. Si restringimos el valor de\(θ\) para que\(\alpha < \theta < \alpha + 2n\pi\), entonces la función

\ (\ begin {eqnarray}\ label {log3}
\ log z=\ ln r +i\ theta\ quad (r> 0,\ alpha <\ theta <\ alpha + 2\ pi),
\ end {eqnarray}\)

con componentes

\ (\ begin {eqnarray*}
u (r,\ theta) =\ ln r,\ quad v (r,\ theta) =\ theta,
\ end {eqnarray*}\)

es una función de valor único y continua en el dominio establecido.

Una rama de una función de múltiples valores\(f\) es cualquier función de valor único\(F\) que es analítica en algún dominio en cada punto\(z\) del cual el valor\(F(z)\) es uno de los valores de\(f\). El requisito de analíticidad, por supuesto,\(F\) impide asumir una selección aleatoria de los valores de\(f\).

Observe que para cada α fijo, la función de valor único (4) es una rama de la función de múltiples valores (3). La función

\ (\ begin {eqnarray}\ label {log4}
\ text {Log} z=\ ln r +i\ Theta\ quad (r> 0, -\ pi <\ theta <\ pi),
\ end {eqnarray}\)

se llama la rama principal.

Un corte de rama es una porción de una línea o curva que se introduce para definir una rama\(F\) de una función de múltiples valores\(f\). Los puntos en el corte de rama\(F\) son puntos singulares de\(F\), y cualquier punto que sea común a todos los cortes de rama de\(f\) se denomina punto de ramificación. El origen y el rayo\(\theta = \alpha\) conforman el corte de rama para la rama (4) de la función logarítmica. El corte de rama para la rama principal (5) consiste en el origen y el\(ray= \pi\). El origen es evidentemente un punto de ramificación para las ramas de la función logarítmica de múltiples valores.

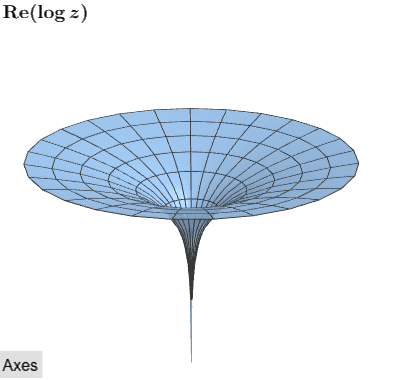
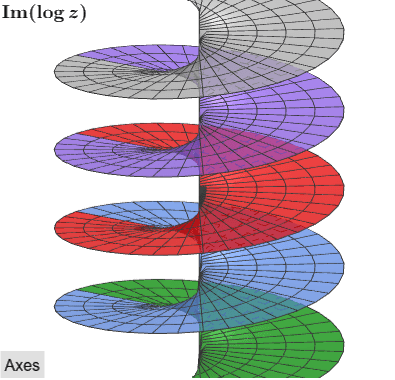
Podemos visualizar la naturaleza de múltiples valores\(logz\) mediante el uso de superficies Riemann. Las siguientes imágenes interactivas muestran los componentes reales e imaginarios de\(log⁡(z)\). Cada rama de la parte imaginaria se identifica con un color diferente.

Se debe tener especial cuidado en el uso de ramas de la función logarítmica, especialmente porque las identidades esperadas que involucran logaritmos no siempre se trasladan del cálculo.

---

Comentario Final

Observe que para\(z≠0\), tenemos

\ (\ begin {eqnarray}\ label {exp001}
e^ {\ log z} =z\ quad\ texto {y}\ quad\ log (e^z) =z+2n\ pi i
\ end {eqnarray}
\)

con\(n\in \mathbb Z \).

Ejemplo\(\PageIndex{3}\)

Calcular\(e^{\log z}\), y\(\log \left(e^z\right)\) para\(z=4i\).

Solución

Si\(z=4i\), entonces\(e^z=e^{4i}\). De ahí

\(\log\left(e^{4i}\right)=4i +2n\pi i\)

con\(n\in \mathbb Z\). Por otro lado, tenemos

\(e^{\log\left(4i\right)}=4i\).