3.2: La Transformación w=1/z

 

 

Considera la ecuación

\(w=\frac{1}{z}\)

que establece una correspondencia uno a uno entre los puntos distintos de cero de los\(w\) planos\(z\) y. Ya que\(z\bar{z}=\left | z \right |^{2}\), el mapeo puede ser descrito por medio de las sucesivas transformaciones

\(g\left ( z \right )=\frac{z}{\left | z \right |^{2}}\).

La primera transformación\(g(z)\) es una inversión con respecto al círculo unitario\(\left | z \right |=1\). Es decir, la imagen de un punto distinto de cero\(z\) es el punto\(g(z)\) con las propiedades

\(\left | g\left ( z \right ) \right |=\frac{1}{\left | z \right |}\)y\(arg\,g(z)=arg\, z\).

Así, los puntos exteriores al círculo\(\left | z \right |=1\) se mapean sobre los puntos distintos de cero interiores a él, y a la inversa. Cualquier punto en el círculo se mapea sobre sí mismo. La segunda transformación\(f\left ( z \right )=\overline{g\left ( z \right )}\) es simplemente un reflejo en el eje real.

Si consideramos la función

\(T\left ( z \right )=\frac{1}{z}\),\(z\neq 0\)

podemos definir\(T\) en el origen y en el punto en el infinito para ser continuos en el plano complejo extendido. Para hacer\(T\) continuo en el plano extendido, entonces, escribimos

\(T(0)=∞\),\(T(∞)=0\), y\(T\left ( z \right )=\frac{1}{z}\)

para los valores restantes de\(z\).

---

Mapeos por\(1/z\)

Una propiedad interesante del mapeo\(w=1/z\) es que transforma círculos y líneas en círculos y líneas.

Esto se puede observar intuitivamente en el siguiente applet. Cosas para probar:

• Seleccione entre una Línea o Círculo.
• Arrastre puntos alrededor de la ventana del lado izquierdo. También puede cambiar la posición de la línea o círculo arrastrando los puntos grises.

GRAFO INTERACTIVO

 

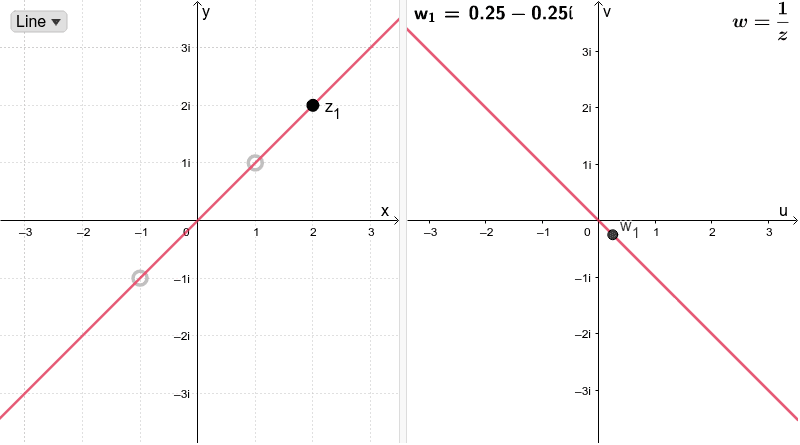
Observe atentamente lo que sucede con los puntos\(w_{1}\),\(w_{2}\) (la imagen de\(z_{1}\) y\(z_{2}\), respectivamente) en el\(uv\) plano -plano, que se muestra en la ventana del lado derecho.

• ¿Qué nota cuando la línea del\(xy\) avión cruza el origen?
• ¿Qué sucede cuando el círculo en el\(xy\) plano cruza el origen?

 

Cuando\(A\),\(B\),\(C\) y\(D\) son todos los números reales que satisfacen la condición\(B^{2}+C^{2}> 4AD\), la ecuación

\(A\left ( x^{2}+y^{2} \right )+Bx+Cx+D=0\)(1)

representa un círculo o línea arbitraria, donde\(A≠0\) para un círculo y\(A=0\) para una línea.

Al usar el método de completar los cuadrados, podemos reescribir la ecuación (1) de la siguiente manera

\(\left ( x+\frac{B}{2A} \right )^{2}+\left ( y+\frac{C}{2A} \right )^{2}=\left ( \frac{\sqrt{B^{2}+C^{2}-4AD}}{2A} \right )^{2}\)

Esto hace evidente la necesidad de condición\(B^{2}+C^{2}>4AD\) cuando\(A≠0\). Cuando\(A=0\), la condición se vuelve\(B^{2}+C^{2}>0\), lo que significa que\(B\) y no\(C\) son ambos cero.

Ahora, usando las relaciones

\(x=\frac{z+\bar{z}}{2}\),\(x=\frac{z-\bar{z}}{2i}\) (2)

podemos reescribir la ecuación (1) en la forma

\(2Az\bar{z}+\left ( B-iC \right )+(B+iC)\bar{z}+2D=0\). (3)

Dado que\(w=1/z\), la ecuación (3) se convierte en

\(2Dw\bar{w}+\left ( B+iC \right )w+(B-iC)\bar{w}+2A=0\)

y el uso de las relaciones

\(u=\frac{w+\bar{w}}{2}\),\(v=\frac{w-\bar{w}}{2i}\), (4)

obtenemos

\(D\left ( u^{2}+v^{2} \right )+Bu-Cv+A=0\)(5)

que también representa un círculo o una línea.

Ahora queda claro a partir de las ecuaciones (1) y (5) que

1. un círculo (que\(A≠0)\) no pasa por el origen\((D≠0)\) en el\(z\) plano se transforma en un círculo que no pasa por el origen en el plano\ w (\);
2. un círculo (\(A≠0)\)A≠ 0 a través del origen\((D=0)\) en el\(z\) plano se transforma en una línea que no pasa por el origen en el\(w\) plano;
3. una línea (que\(A=0)\) no pasa por el origen\((D≠0)\) en el\(z\) plano se transforma en un círculo a través del origen en el\(w\) plano;
4. una línea (\(A=0)\)a través del origen\((D=0)\) en el\(z\) plano se transforma en una línea a través del origen en el\(w\) plano.

Ejercicio\(\PageIndex{1}\)

Verificar que la expresión se\(D\left ( u^{2}+v^{2} \right )+Bu-Cv+A=0\) pueda obtener de (1) usando las relaciones (2) y (4).