4.1: Curvas en el Plano Complejo

Supongamos que las funciones continuas de valor real\(x=x(t)\)\(y=y(t)\),,\(a≤t≤\) b, son ecuaciones paramétricas de una curva\(C\) en el plano complejo. Si utilizamos estas ecuaciones como las partes real e imaginaria en\(z=x+iy\), podemos describir los puntos\(z\) sobre\(C\) por medio de una función de valor complejo de una variable real\(t\) llamada parametrización de\(C\):

\(z(t)=x(t)+iy(t)\),\(a≤t≤b\). (1)

El punto\(z(a)=x(a)+iy(a)\) o\(z_{0}=\left ( x\left ( a \right ),y\left ( a \right ) \right )\) se llama el punto inicial de\(C\) y\(z(b)=x(b)+iy(b)\) o\(z_{1}=\left ( x\left ( b \right ) ,y\left ( b \right )\right )\) es su punto terminal. La expresión también\(z(t)=x(t)+iy(t)\) podría interpretarse como una función vectorial bidimensional. En consecuencia,\(z(a)\) y\(z(b)\) pueden ser interpretados como vectores de posición. Como tt varía de\(t=a\) a,\(t=b\) podemos imaginarnos que la curva\(C\) sea trazada por la punta de flecha móvil de\(z(t)\). Esto se puede apreciar en el siguiente applet con\(0≤t≤1\).

Presiona Inicio para animar. Se pueden mover los puntos para cambiar la curva.

Por ejemplo, las ecuaciones paramétricas\(x=cos\,⁡t\)\(y=sin⁡\,t\),\(0\leq t\leq 2\pi \), describen un círculo unitario centrado en el origen. Una parametrización de este círculo es\(z(t)=cos\,⁡t+i\,sin⁡\,t\), o\(z\left ( t \right )=e^{it}\),\(0\leq t\leq 2\pi \).

Presiona Inicio para animar.

---

Contornos

Las nociones de curvas en el plano complejo que son lisas, lisas por partes, simples, cerradas y simples cerradas se formulan fácilmente en términos de la función vectorial (1). Supongamos que la derivada de (1) es\(z′(t)=x′(t)+iy′(t)\). Decimos que una curva\(C\) en el plano complejo es suave si\(z′(t)\) es continua y nunca cero en el intervalo\(a≤t≤b\). Como se muestra en la Figura 2, dado que el vector z′ (t) no\(\) es cero\(P\) en ningún punto\(C\), el vector\(z′(t)\) es tangente a\(C\) at\(P\). Así, una curva suave tiene una tangente de giro continuo; o en otras palabras, una curva suave no puede tener esquinas ni cúspides afiladas. Ver Figura 2.

Figura 1:\(z′(t)=x′(t)+iy(t)\) como vector tangente.

Figura 2: La curva no\(C\) es lisa ya que tiene cúspide.

Una curva lisa por tramos\(C\) tiene una tangente de giro continuo, excepto posiblemente en los puntos donde las curvas suaves del componente\(C_{1},C_{2},\cdots ,C_{n}\) se unen entre sí.

Figura 3: Una curva lisa por tramos.

Una curva\(C\) en el plano complejo se dice que es un simple si\(z\left ( t_{1} \right )\neq z\left ( t_{2} \right )\) para\(t_{1}\neq t_{2}\), excepto posiblemente para\(t=a\) y\(t=b\). \(C\)es una curva cerrada si\(z(a)=z(b)\).

Figura 4: Curva simple.

Figura 5: Curva no simple.

\(C\)es una curva cerrada simple si\(z\left ( t_{1} \right )\neq z\left ( t_{2} \right )\) para\(t_{1}≠t_{2}\) y\(z(a)=z(b)\).

Figura 4: Curva cerrada simple.

Figura 5: Curva cerrada no simple.

En análisis complejos, una curva lisa por tramos\(C\) se denomina contorno o trayectoria. Definimos la dirección positiva en un contorno\(C\) para que sea la dirección en la curva correspondiente a valores crecientes del parámetro\(t\). También se dice que la curva\(C\) tiene orientación positiva. En el caso de un simple contador cerrado\(C\), la dirección positiva corresponde a la dirección contraria a las agujas del reloj. Por ejemplo, el círculo\(z\left ( t \right )=e^{it}\),\(0\leq t\leq 2\pi \), tiene orientación positiva. La dirección negativa en un contorno\(C\) es la dirección opuesta a la dirección positiva. Si\(C\) tiene una orientación, la curva opuesta, es decir, una curva con orientación opuesta, se denota por\(−C\). En una curva cerrada simple, la dirección negativa corresponde a la dirección de las agujas del reloj. Por ejemplo, el círculo\(z\left ( t \right )=e^{-it}\),\(0\leq t\leq 2\pi \), tiene orientación negativa.

Figura 6: Orientado positivamente.

Figura 7: Orientado negativamente.

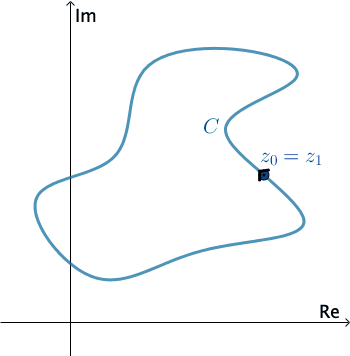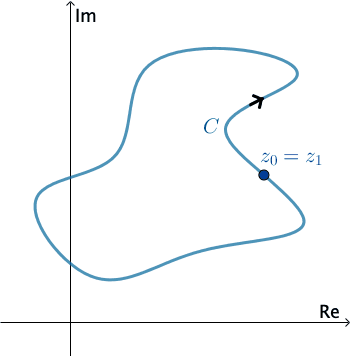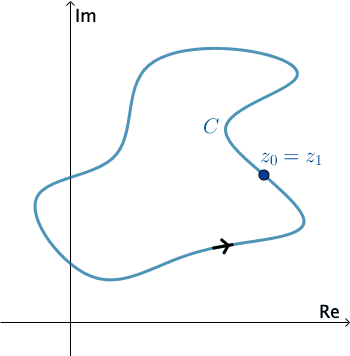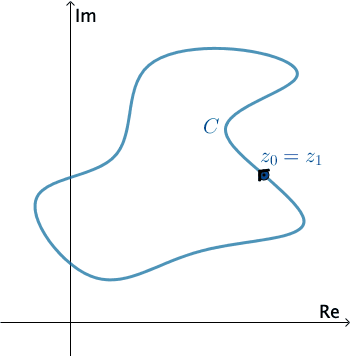
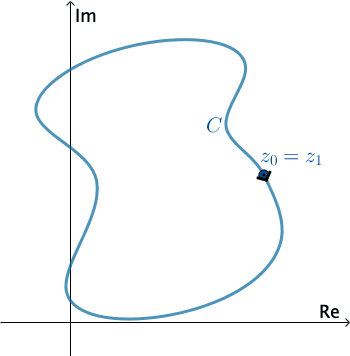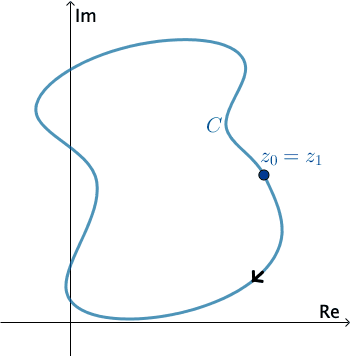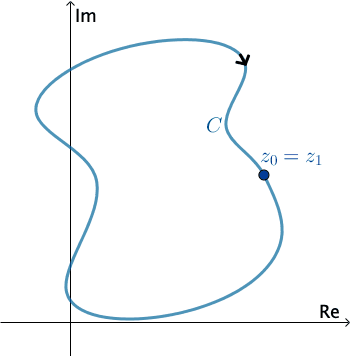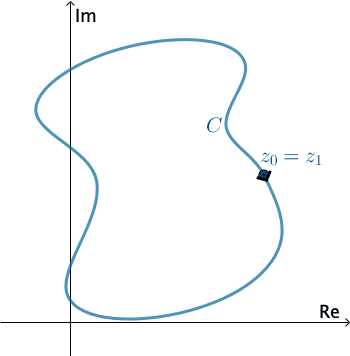
Presiona Inicio para animar. Se puede cambiar la dirección de\(C\) .

Ejercicio\(\PageIndex{1}\)

Ejercicio: No hay parametrización única para un contorno\(C\). Debe verificar que

\(z\left ( t \right )=e^{it}=cos\,t+i\,sin\,t\),\(0\leq t\leq 2\pi \)

\(z\left ( t \right )=e^{2\pi it}=cos\left (2\pi t\right )+i\,sin\left (2\pi  t \right )\),\(0\leq t\leq 1 \)

\(z\left ( t \right )=e^{\pi /2it}=cos\left (\frac{\pi}{2}t \right )+i\,sin\left (\frac{\pi}{2}t \right )\),\(0\leq t\leq 4\)

son todas las parametrizaciones, orientadas en la dirección positiva, para el círculo unitario\(\left | z \right |=1\).