5.4: Clasificación de Singularidades

La porción

\ (\ begin {eqnarray}\ label {principal}
\ frac {b_1} {z-z_0} +\ frac {b_2} {(z-z_0) ^2} +\ frac {b_3} {(z-z_0) ^3} +\ cdots
\ end {eqnarray}\)

de la serie Laurent, que involucra poderes negativos de\(z−z_0,\), se llama la parte principal de\(z−z_0,\) at\(z_0\). El coeficiente\(b_1\) en la ecuación (1), resulta jugar un papel muy especial en el análisis complejo. Se le da un nombre especial: el residuo de la función\(f(z)\). En esta sección nos centraremos en la parte principal para identificar el punto singular aislado\(z_0\) como uno de los tres tipos especiales.

---

Polos

Si la parte principal de\(f\) at\(z_0\) contiene al menos un término distinto de cero pero el número de tales términos es solo finito, entonces existe un entero\(m≥1\) tal que

\(b_m\neq 0 \quad\text{and} \quad b_{k}=0\quad \text{for}\quad k\gt m.\)

En este caso, el punto singular aislado\(z_0\) se denomina polo de orden\(m\). Un polo de orden generalmente\(m=1\) se conoce como un poste simple.

Ejemplos

Considerar las funciones

\(f(z)=\dfrac{e^z-1}{z^2},\qquad g(z)=\frac{\cos z}{z^2}\qquad\text{and}\qquad h(z)=\frac{\sinh z}{z^4},\)

con una singularidad aislada en\(z_0=0\). Las figuras 1, 2 y 3 muestran los retratos de fase mejorados de estas funciones definidas en el cuadrado\(|\text{Re }z|\lt 3\) y\(|\text{Im }z|\lt 3\).

Figura 1:\(f(z)=\dfrac{e^z-1}{z^2}\)

Figura 2:\(g(z)=\dfrac{\cos z}{z^2}\)

Figura 3:\(h(z)=\dfrac{\sinh z}{z^4}\)

Ahora a partir de los retratos de fase mejorados podemos observar que de hecho\(z_0=0\) es un polo cuyo orden también se puede ver fácilmente, es solo el número de rayos isocromáticos de un color (elegido arbitrariamente) los que se encuentran en ese punto. Así podemos afirmar que\(f\),\(g\) y hh tienen polos de orden 1, 2 y 3; respectivamente. Para confirmar esto calculemos la representación de la serie Laurent centrada en\(0\). Primero observa que

\ (\ begin {eqnarray*}
f (z) &=&\ frac {1} {z^2}\ left [\ left (1 + z +\ frac {z^2} {2!} +\ cdots\ derecha) - 1\ derecha]\\
&=&\ frac {1} {z}
+\ frac {1} {2!} +\ frac {z} {3!} +\ frac {z^2} {4!} +\ cdots,\ quad (0\ lt|z|\ lt\ infty).
\ end {eqnarray*}\)

Así podemos ver que\(f\) tiene un poste sencillo. Por otro lado

\ (\ begin {eqnarray*}
g (z) &=&\ frac {1} {z^2}\ left (1-\ frac {z^2} {2!} +\ frac {z^4} {4!} -\ cdots
\ derecha)\\
&=&\ frac {1} {z^2} -\ frac {1} {2!} +\ frac {z^2} {4!} -\ cdots,\ quad (0\ lt|z|\ lt\ infty)
\ end {eqnarray*}
\)

entonces gg tiene un polo de orden 2. Por último,\(h\) tiene un polo de orden 3 desde

\ (\ begin {eqnarray*}
h (z) &=&\ frac {1} {z^4}\ left (z+\ frac {z^3} {3!} +\ frac {z^5} {5!} +\ cdots\ derecha)\\
&=&\ frac {1} {z^3} +\ frac {1} {3!} \ cdot
\ frac {1} {z} +\ frac {z} {5!} +\ frac {z^3} {7!} +\ cdots,\ quad (0\ lt|z|\ lt\ infty).
\ end {eqnarray*}
\)

---

Singularidad removible

Cuando cada\(b_n\) es cero, para que

\ (\ begin {eqnarray}\ label {residue003}
f (z) =\ sum_ {n=0} ^ {\ infty} a_n (z-z_0) ^n,\ quad (0\ lt |z-z_0|\ lt R_2).
\ end {eqnarray}\)

En este caso,\(z_0\) se conoce como punto singular removible. Tenga en cuenta que el residuo en un punto singular removible es siempre cero. Si definimos, o posiblemente redefinimos,\(f\) en de\(z_0\) manera que\(f(z_0) = a_0\), la expansión (2) se vuelve válida en todo el disco\(|z - z_0| \lt R_2\). Dado que una serie de potencias siempre representa una función analítica interior a su círculo de convergencia, se deduce que\(f\) es analítica en el\(z_0\) momento en que se le asigna el valor\(a_0\) allí. La singularidad\(z_0\) es, por lo tanto, eliminada.

Ejemplos

Considerar las funciones

\(f(z)=\frac{1-\cos z}{z^2},\qquad g(z)=\frac{\sin z}{z}\qquad\text{and}\qquad h(z)=\frac{z}{e^z-1}.\)

La figura muestra los retratos de fase mejorados de estas funciones definidas en el cuadrado\(|\text{Re }z|\lt 8\) y\(|\text{Im }z|\lt 8\).

Figura 4:\(f(z)=\dfrac{1-\cos z}{z^2}\)

Figura 5:\(g(z)=\dfrac{\sin z}{z}\)

Figura 6:\(h(z)=\dfrac{z}{e^z-1}\)

Notamos que\(f\) tiene una singularidad en\(z_0=0\) pero en este caso la trama no muestra líneas isocromáticas que se encuentran en ese punto. Esto indica que la singularidad podría ser removible.

Podemos confirmar esta afirmación fácilmente desde la representación de la serie Laurent:

\ (\ begin {eqnarray*}
f (z) &=&\ frac {1} {z^2}\ left [1-\ left (1-\ frac {z^2} {2!} +\ frac {z^4} {4!} -\ frac {z^6} {6!} +\ cdots
\ derecha)\ derecha]\\
&=&\ frac {1} {2!} -\ frac {z^2} {4!} +\ frac {z^4} {6!} -\ cdots,\ quad (0\ lt |z|\ lt\ infty).
\ end {eqnarray*}\)

En este caso, cuando se asigna el valor\(f(0)=1/2\),\(f\) se vuelve entero. Además, podemos observar intuitivamente que dado que\(z=0\) es un punto singular removible de\(f\), entonces\(f\) debe ser analítico y delimitado en algún barrio eliminado\(0\lt |z|\lt \varepsilon\).

Ejercicio\(\PageIndex{1}\)

Encuentre la expansión de la serie Laurent para\(g\) y\(h\) para confirmar que tienen singularidades removibles en\(z_0=0\).

---

Singularidad esencial

Si un número infinito de los coeficientes\(b_n\) en la parte principal (1) son distintos de cero, entonces\(z_0=0\) se dice que es un punto singular esencial de\(f\).

Ejemplos

La función

\(f(z)=\exp\left(\frac{1}{z}\right)\)

tiene una singularidad esencial a\(z_0=0\) partir de

\ (\ begin {eqnarray*}
f (z) &=&1+\ frac {1} {1!} \ cdot\ frac {1} {z} +\ frac {1} {2!} \ cdot
\ frac {1} {z^2} +\ cdots\\
&=&\ sum_ {n=0} ^ {\ infty}\ frac {1} {n!} \ cdot\ frac {1} {z^n},\ quad (0\ lt |z|\ lt\ infty).
\ end {eqnarray*}\)

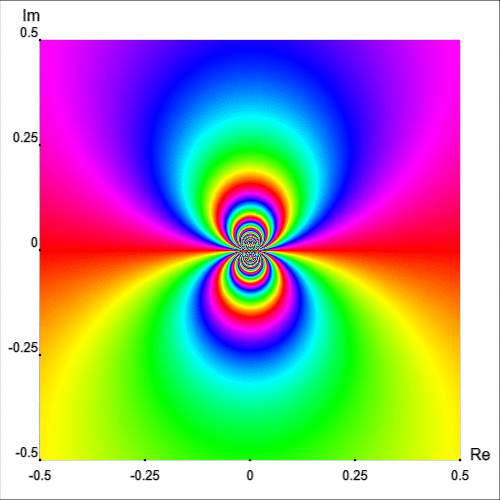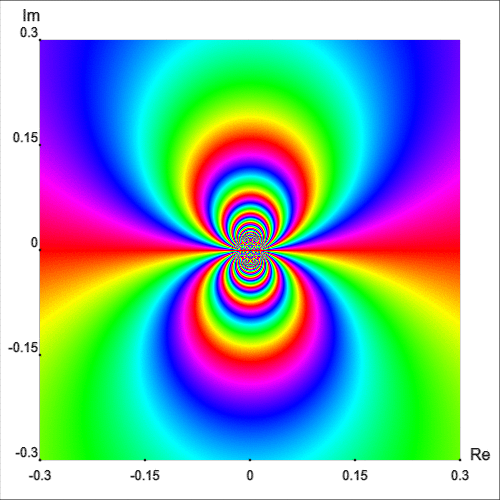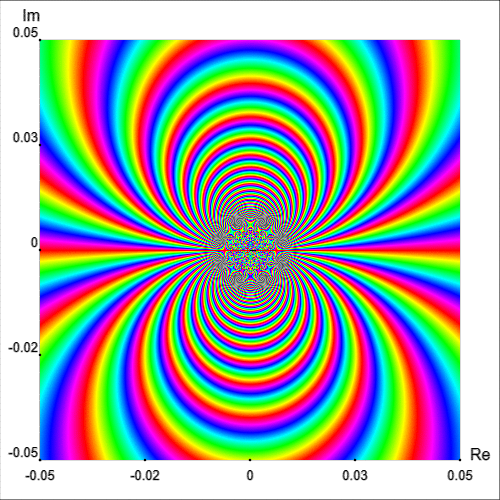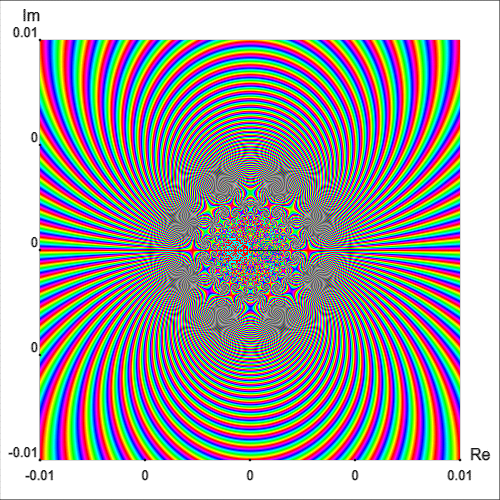
La Figura 7 muestra el retrato mejorado de\(f\) en el cuadrado\({|\text{Re }z|\lt 0.5}\) y\({|\text{Im }z|\lt 0.5}\). Lo primero que notamos es que el comportamiento de\(f\) cerca del punto singular esencial es bastante irregular. Observe cómo las líneas isocromáticas, cercanas\(z_0=0\), forman infinitas formas autónomas en forma de ocho.

Figura 7:\(\) definido en\(\).

De hecho, un barrio de\(z_0=0\) intersecta infinitamente muchas líneas isocromáticas del retrato de fase de un mismo color [Wegert, 2012, p. 181]. Este hecho se puede apreciar intuitivamente trazando el retrato de fase simple de\(exp\,(1/z)\) en una región más pequeña, como se muestra en la Figura 8.

Figura 8: Retrato de fase simple: Una vista más cercana a la singularidad esencial.

Otro ejemplo con una singularidad esencial en el origen es la función

\(g(z) = (z − 1) \cos\left(\frac{1}{z}\right)\)

La Figura 9 muestra el retrato de fase mejorado de\(g\) en el cuadrado\(|\text{Re } z| \lt 0.3\) y\(|\text{Im } z| \lt 0.3\).

Figura 9:\((z − 1) \cos\,(1/z)\)

Ejercicio\(\PageIndex{2}\)

Encuentre la expansión de la serie Laurent\((z − 1) \cos\,(1/z)\) para confirmar que tiene una singularidad esencial en\(z_0=0\).

---

observación final

Los retratos de fase son bastante útiles para comprender el comportamiento de las funciones cerca de singularidades aisladas. Las figuras 7 y 9 indican un comportamiento bastante salvaje de estas funciones en un barrio de singularidades esenciales, en comparación con polos y puntos singulares removibles. Además, pueden utilizarse para explorar y comprender, desde un punto de vista geométrico, resultados matemáticos más abstractos como el Gran Teorema de Picard, que nos dice que cualquier función analítica con una singularidad esencial en\(z_0\) toma todos los valores complejos posibles ( con a lo sumo una sola excepción) infinitamente a menudo en cualquier vecindario de\(z_0\).

Figura 10:\(\displaystyle\sum_{k=-\infty}^{\infty}q^{k^2}z^k\)