6.1: Aplicaciones de Mappings conformes

Última actualización
Guardar como PDF

Page ID: 114141

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Hidrodinámica

Si tenemos un fluido (en estado estacionario) incompresible, no viscoso, estamos interesados en encontrar su campo de velocidad

\(\mathbf V (x,y)= \left(u(x,y), v(x,y)\right).\)

A partir del análisis vectorial sabemos que 'incompresible' significa que la divergencia\(\text{div}\,\mathbf V =0.\) (Decimos\(\mathbf V\) es libre de divergencia. ) Suponemos que también\(\mathbf V\) es un flujo potencial y por lo tanto está libre de circulación; es decir,\(\mathbf V = \text{grad } \phi\) para algunos\(\phi\) se llama el potencial de velocidad. Así\(\phi\) es armónico porque

\(\nabla^2\phi = \text{div } \text{grad }\phi = \text{div } \mathbf V=0.\)

Así cuando\(\phi\) resolvemos para podemos obtener\(\mathbf V\) tomando\(\mathbf V = \text{grad } \phi\). Eso es

\ (\ begin {eqnarray*}
u=\ frac {\ parcial\ phi} {\ parcial x},\ quad v=\ frac {\ parcial\ phi} {\ parcial y}.
\ end {eqnarray*}\)

El conjugado\(ψ\) de la función armónica\(ϕ\) (que existirá en cualquier región conectada simple) se llama función stream, y la función analítica

\(F=\phi +i\psi\)

se llama el potencial complejo.

La función stream debe satisfacer

\ (\ begin {eqnarray*}
u=\ frac {\ parcial\ psi} {\ parcial y},\ quad v=-\ frac {\ parcial\ psi} {\ parcial x}.
\ end {eqnarray*}\)

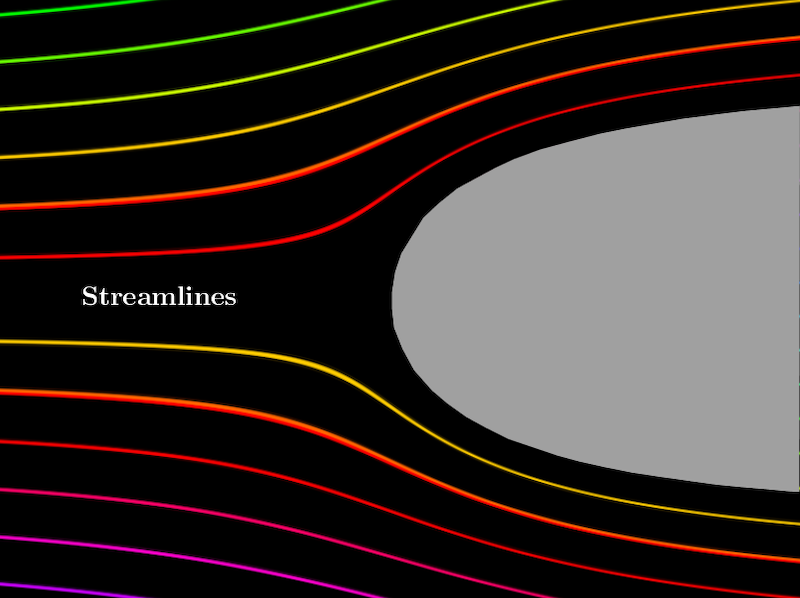
Finalmente, las líneas de constante\(ψ\) tienen\(V\) como sus tangentes, por lo que las líneas de constante\(ψ\) pueden interpretarse como las líneas a lo largo de las cuales se mueven las partículas de fluido; de ahí el nombre de función stream.