6.4: Superficie aerodinámica Joukowsky
- Page ID
- 114140
El mapa de Joukowsky
Un ejemplo bien conocido de una función conforme es el mapa Joukowsky
\ (\ begin {eqnarray}\ label {jouk}
w= z+ 1/z.
\ end {eqnarray}\)
Fue utilizado por primera vez en el estudio del flujo alrededor de las alas de los aviones por el pionero investigador ruso de aerodinámica Nikolai Zhukovskii (Joukowsky).
Desde
\(\frac{d}{dz}w=1-\frac{1}{z^2}=0\quad \text{if and only if}\quad z=\pm 1,\)
la función (1) es conforme excepto en los puntos críticos así\(z=±1\) como la singularidad\(z=0\), donde no está definida.
Si\(z = e^{i\theta}\) se encuentra en el círculo unitario, entonces
\(w =e^{i\theta}+e^{-i\theta}=2\cos \theta,\)
yace en el eje real, con\(-2\leq w\leq 2\). Así, el mapa de Joukowsky aplasta el círculo unitario hasta el segmento de línea real\([−2,2]\). Las imágenes de puntos fuera del círculo unitario llenan el resto del\(w\) plano, al igual que las imágenes de los puntos (distintos de cero) dentro del círculo unitario. En efecto, si resolvemos (1) para\(z\), tenemos
\(z=\frac{1}{2}\left(w\pm \sqrt{w^2-4}\right).\)
Vemos que cada\(w\) excepto\(±2\) viene de dos puntos diferentes\(z\); porque\(w\) no en el segmento de línea crítica\([−2,2]\), un punto (con el signo menos) se encuentra dentro y uno (con el signo más) se encuentra fuera del círculo unitario, mientras que si\(−2<w<2\), ambos puntos se encuentran en la unidad círculo y una línea vertical común.
Por lo tanto, el mapa de Joukowski define un mapeo conforme uno a uno desde\(|z|>1\), el exterior del círculo unitario, hacia el exterior del segmento lineal, es\([−2,2]\) decir,. e.\(\mathbb C \setminus [-2, 2]\)
En la Figura 4 podemos observar que los círculos concéntricos\(|z|=r>1\) se mapean a elipses con focos\(±2\) en el\(w\) plano.
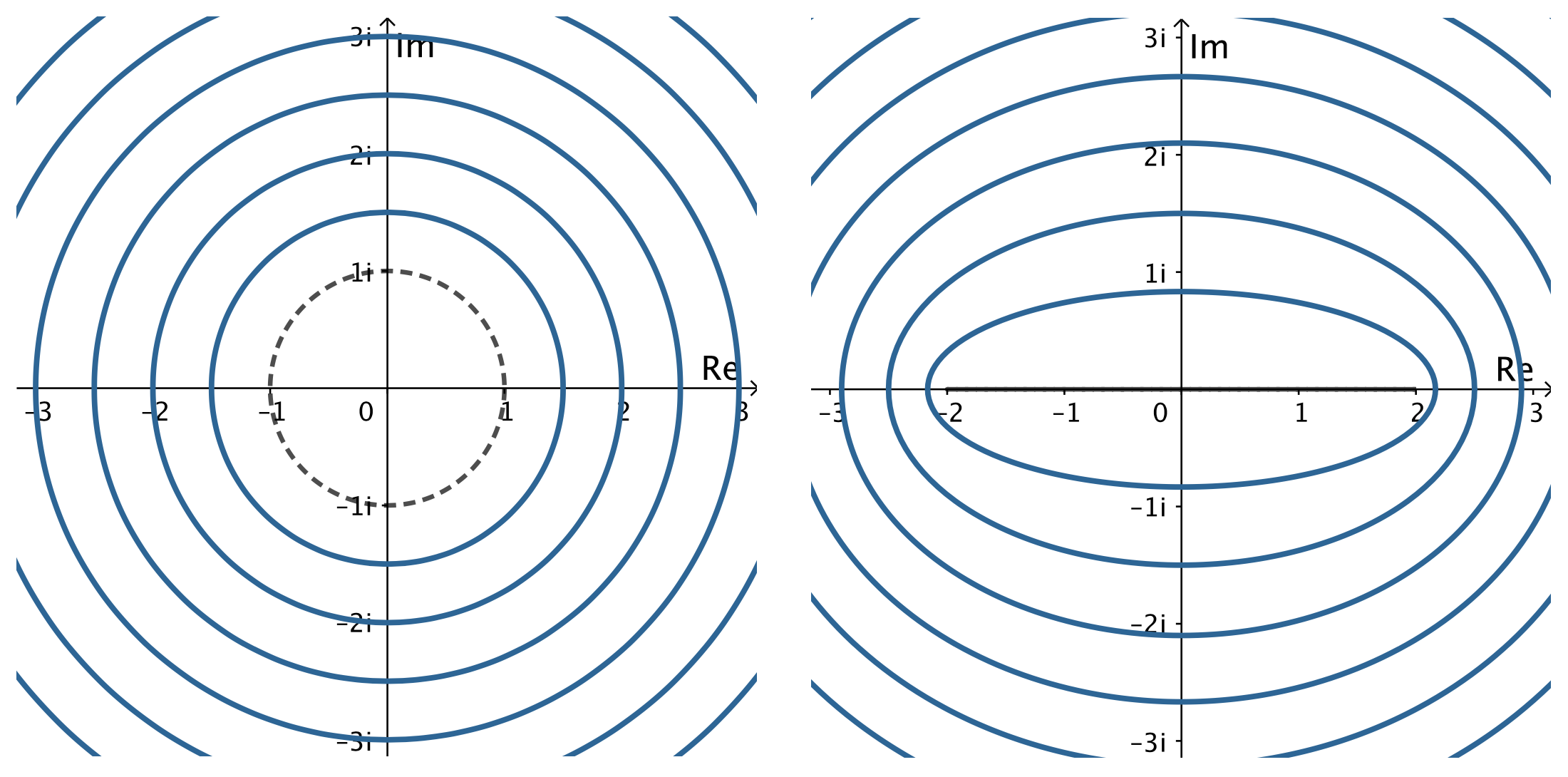
El efecto sobre círculos no centrados en el origen es más interesante. Las curvas de imagen toman una amplia variedad de formas. Cuando el círculo pasa por el punto singular\(z=1\), entonces su imagen ya no es suave, sino que tiene una cúspide en\(w=2\) y cuando el círculo pasa a través de\(z=−1\) la cúspide está en\(w=−2\). Algunas de las curvas de imagen asumen la forma de la famosa sección transversal a través de un ala o perfil aerodinámico idealizado, también conocido como el perfil aerodinámico Joukowsky.
Puedes explorar el mapa de Joukowsky en el applet a continuación. Arrastre alrededor del centro del círculo. Arrastre los deslizadores para aplicar la asignación o cambiar el radio. Haga clic en el botón para ver valores predefinidos.
Fluye alrededor del perfil aerodinámico Joukowsky
Considere ahora el flujo uniforme alrededor del círculo unitario con circulación\(C\) y velocidad\(U>0\) dadas por el complejo potencial
\ (\ begin {eqnarray}\ label {eq1}
F (z) =Uz+\ frac {U} {z} -\ frac {i C} {2\ pi}\ log z.
\ end {eqnarray}\)
Podemos utilizar la transformación lineal
\(T(z)=-0.15+0.23i + 0.23\sqrt{13\cdot 2} z\)
para mapear este flujo alrededor\(|z|=1\) del flujo alrededor del círculo\(c_1\) con centro\(z_1=−0.15+0.23i\) y radio\(r=0.23\sqrt{13\cdot 2}\)
Finalmente, aplicando el mapa Joukowsky (1), podemos obtener un flujo uniforme con circulación alrededor del perfil aerodinámico Joukowsky.
La siguiente simulación muestra el flujo uniforme pasado el cilindro circular\(c_1\) y su transformación al perfil aerodinámico Joukowsky. Arrastre los controles deslizantes para explorar:
- Slider\(U\) = velocidad.
- Slider\(C\) = circulación.
- Slider\(T\) = aplicar transformación.
Presiona el botón Trazar para mostrar las líneas de racionalización.


