7.2: Fracciones propias, fracciones impropias y números mixtos

Última actualización
Guardar como PDF

Page ID: 161162

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

ser capaz de distinguir entre fracciones propias, fracciones impropias y números mixtos
poder convertir una fracción impropia en un número mixto
poder convertir un número mixto en una fracción impropia

Ahora que sabemos qué son las fracciones positivas, consideramos tres tipos de fracciones positivas: fracciones propias, fracciones impropias y números mixtos.

Fracciones propias positivas

Definición: Fracción apropiada positiva

Las fracciones en las que el número entero en el numerador es estrictamente menor que el número entero en el denominador se denominan fracciones propiamente positivas. En la recta numérica, las fracciones propias se ubican en el intervalo de 0 a 1. Las fracciones positivas propiamente dichas son siempre menores a una.

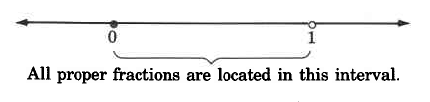
$Una línea numérica. 0 está marcado con un punto negro, y 1 está marcado con un punto hueco. La distancia entre los dos está etiquetada, todas las fracciones propias se ubican en este intervalo.$

El círculo cerrado en 0 indica que 0 está incluido, mientras que el círculo abierto en 1 indica que 1 no está incluido.

Algunos ejemplos de fracciones propias positivas son

$\dfrac{1}{2}$,$\dfrac{3}{5}$,$\dfrac{20}{27}$, y$\dfrac{106}{255}$

Tenga en cuenta que$1 < 2$$3 < 5$,$20 < 27$,, y$106 < 225$.

Fracciones impropias positivas

Definición: Fracciones impropias positivas

Las fracciones en las que el número entero en el numerador es mayor o igual que el número entero en el denominador se denominan fracciones impropias positivas. En la recta numérica, las fracciones impropias se encuentran a la derecha de (e incluyendo) 1. Las fracciones impropias positivas son siempre mayores o iguales a 1.

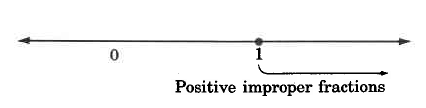
$Una línea numérica. 0 está etiquetada, y 1 está marcada con un punto hueco. Se dibuja una flecha a la derecha, etiquetada Fracciones impropias Positivas.$

Algunos ejemplos de fracciones impropias positivas son

$\dfrac{3}{2}$,$\dfrac{8}{5}$,$\dfrac{4}{4}$, y$\dfrac{105}{16}$

Tenga en cuenta que$3 \ge 2, 8 \ge 5, 4 \ge 4$, y$105 \ge 16$.

Números Mixtos Positivos

Definición: Números Mixtos Positivos

Un número de la forma$\text{nonzero whole number} + \text{proper fraction}$ se llama un número mixto positivo. Por ejemplo, 2$\dfrac{3}{5}$ es un número mixto. En la recta numérica, los números mixtos se ubican en el intervalo a la derecha de (e incluyendo) 1. Los números mixtos son siempre mayores o iguales a 1.

$Una línea numérica. 0 está etiquetada, y 1 está marcada con un punto hueco. Se dibuja una flecha a la derecha, etiquetada con números mixtos positivos.$

Relacionar fracciones impropias positivas y números mixtos positivos

Dos hechos sugieren una relación entre fracciones impropias y números mixtos. La primera es que las fracciones impropias y los números mixtos se localizan en el mismo intervalo en la recta numérica. El segundo hecho, que los números mixtos son la suma de un número natural y una fracción, se puede apreciar haciendo las siguientes observaciones.

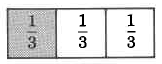
Divide una cantidad entera en 3 partes iguales.

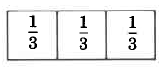
$Un rectángulo dividido en tres partes iguales con barras verticales. Cada parte contiene la fracción, un tercio.$

Ahora, considere los siguientes ejemplos observando las respectivas áreas sombreadas.

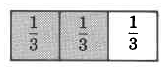
$Un rectángulo dividido en tres partes iguales con barras verticales. Cada parte contiene la fracción, un tercio. Las dos partes más a la izquierda están sombreadas.$

En la región sombreada, hay 2 un tercio, o$\dfrac{2}{3}$.

$2 (\dfrac{1}{3}) = \dfrac{2}{3}$

$Un rectángulo dividido en tres partes iguales con barras verticales. Cada parte contiene la fracción, un tercio. Las tres partes están sombreadas.$

Hay 3 un tercio, o$\dfrac{3}{3}$, o 1.

$3(\dfrac{1}{3}) = \dfrac{3}{3}$o 1

Por lo tanto,

$\dfrac{3}{3} = 1$

Fracción impropia = número entero.

$Un rectángulo dividido en tres partes iguales con barras verticales. Cada parte contiene la fracción, un tercio. Las tres partes están sombreadas.$ $Un rectángulo dividido en tres partes iguales con barras verticales. Cada parte contiene la fracción, un tercio. Una parte está sombreada.$

Hay 4 un tercio, o$\dfrac{4}{3}$, o 1 y$\dfrac{1}{3}$.

$4(\dfrac{1}{3}) = \dfrac{4}{3}$o 1 y$\dfrac{1}{3}$

Los términos 1 y se$\dfrac{1}{3}$ pueden representar como$1 + \dfrac{1}{3}$$1 \dfrac{1}{3}$

Por lo tanto,

$\dfrac{4}{3} = 1 \dfrac{1}{3}.$

fracción mpropia= número mixto.

Hay 5 un tercio, o$\dfrac{5}{3}$, o 1 y$\dfrac{2}{3}$.

$5(\dfrac{1}{3}) = \dfrac{5}{3}$o 1 y$\dfrac{2}{3}$

Los términos 1 y se$\dfrac{2}{3}$ pueden representar como$1 + \dfrac{2}{3}$ o$1\dfrac{2}{3}$.

Por lo tanto,

$\dfrac{5}{3} = 1 \dfrac{2}{3}$.

Fracción impropia = número mixto.

Hay 6 un tercio, o$\dfrac{6}{3}$, o 2.

$6(\dfrac{1}{3}) = \dfrac{6}{3} = 2$

Por lo tanto,

$\dfrac{6}{3} = 2$

Fracción impropia = número entero.

El siguiente dato importante se ilustra en los ejemplos anteriores.

Número Mixto = Número Natural + Fracción Propia Los números
mixtos son la suma de un número natural y una fracción propia. Número mixto = (número natural) + (fracción propia)

Por ejemplo se$1 \dfrac{1}{3}$ puede expresar como$1 + \dfrac{1}{3}$ La fracción se$5 \dfrac{7}{8}$ puede expresar como$5 + \dfrac{7}{8}$.

Es importante señalar que un número como$5 + \dfrac{7}{8}$ no indica multiplicación. Para indicar multiplicación, necesitaríamos usar un símbolo de multiplicación (como$\cdot$)

Ejemplo$\PageIndex{1}$

$5 \dfrac{7}{8}$significa$5 + \dfrac{7}{8}$ y no$5 \cdot \dfrac{7}{8}$, lo que significa 5 veces$\dfrac{7}{8}$ o 5 multiplicado por$\dfrac{7}{8}$.

Así, los números mixtos pueden ser representados por fracciones impropias, y las fracciones impropias pueden ser representadas por números mixtos.

Conversión de fracciones impropias a números mixtos

Para entender cómo podríamos convertir una fracción impropia a un número mixto, consideremos la fracción,$\dfrac{4}{3}$.

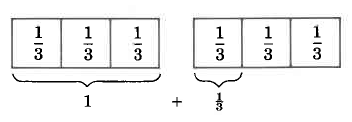
$\begin{array} {rcl} {\dfrac{4}{3}} & = & {\underbrace{\dfrac{1}{3} + \dfrac{1}{3} + \dfrac{1}{3}}_{1} + \dfrac{1}{3}} \\ {} & = & {1 + \dfrac{1}{3}} \\ {} & = & {1\dfrac{1}{3}} \end{array}$

Podemos ilustrar un procedimiento para convertir una fracción impropia a un número mixto usando este ejemplo. Sin embargo, la conversión se logra más fácilmente dividiendo el numerador por el denominador y usando el resultado para escribir el número mixto.

Convertir una fracción impropia en un número mixto
Para convertir una fracción impropia en un número mixto, divida el numerador por el denominador.

La parte del número entero del número mixto es el cociente.
La parte fraccionaria del número mixto es el resto escrito sobre el divisor (el denominador de la fracción impropia).

Conjunto de Muestras A

Convertir cada fracción impropia a su número mixto correspondiente.

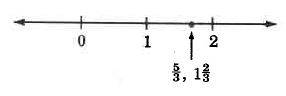
$\dfrac{5}{3}$Divide 5 por 3.

Solución

$División larga. 5 dividido por 3 es uno, con un resto de 2. 1 es la parte del número entero, 2 es el numerador de la parte fraccionaria, y 3 es el denominador de la parte fraccionaria.$

La fracción impropia$\dfrac{5}{3} = 1 \dfrac{2}{3}$.

$Una línea numérica con marcas para 0, 1 y 2. Entre 1 y 2 hay un punto para cinco tercios, o uno y dos tercios.$

Conjunto de Muestras A

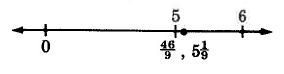
$\dfrac{46}{9}$Divide 46 por 9.

Solución

$División larga. 46 dividido por 9 es 5, con un resto de 1. 5 es la parte del número entero, 1 es el numerador de la parte fraccionaria, y 9 es el denominador de la parte fraccionaria.$

La fracción impropia$\dfrac{46}{9} = 5 \dfrac{1}{9}$.

$Una línea numérica con marcas para 0, 5 y 6. Entre 5 y 6 hay un punto que muestra la ubicación de cuarenta y seis novenas, o cinco y una novena.$

Conjunto de Muestras A

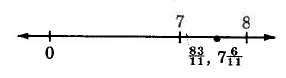
$\dfrac{83}{11}$Divide 83 por 11.

Solución

$División larga. 83 dividido por 11 es 7, con un resto de 6. 7 es la parte del número entero, 6 es el numerador de la parte fraccionaria, y 11 es el denominador de la parte fraccionaria.$

La fracción impropia$\dfrac{83}{11} = 7 \dfrac{6}{11}$.

$Una línea numérica con marcas para 0, 7 y 8. Entre 7 y 8 hay un punto que muestra la ubicación de ochenta y tres once, o siete y seis once.$

Conjunto de Muestras A

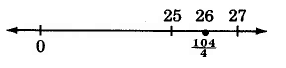
$\dfrac{104}{4}$Divide 104 por 4.

Solución

$División larga. 104 dividido por 4 es 26, con un resto de 0. 26 es la parte del número entero, 0 es el numerador de la parte fraccionaria, y 4 es el denominador de la parte fraccionaria.$

\ (\ dfrac {104} {4} = 26\ dfrac {0} {4} = 26

La fracción impropia$\dfrac{104}{4} = 26$.

$Una línea numérica con marcas para 0, 25, 26 y 27. 26 está marcada con un punto, mostrando la ubicación de ciento cuatro cuartos.$

Conjunto de práctica A

Convertir cada fracción impropia a su número mixto correspondiente.

$\dfrac{9}{2}$

Responder: $4\dfrac{1}{2}$

Conjunto de práctica A

$\dfrac{11}{3}$

Responder: $3\dfrac{2}{3}$

Conjunto de práctica A

$\dfrac{14}{11}$

Responder: $1\dfrac{3}{11}$

Conjunto de práctica A

$\dfrac{31}{13}$

Responder: $2\dfrac{5}{13}$

Conjunto de práctica A

$\dfrac{79}{4}$

Responder: $19\dfrac{3}{4}$

Conjunto de práctica A

$\dfrac{496}{8}$

Responder: 62

Conversión de números mixtos a fracciones impropias

Para entender cómo convertir un número mixto en una fracción impropia, recordaremos

número mixto = (número natural) + (fracción propia)

y considere el siguiente diagrama.

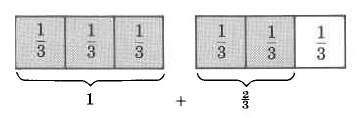
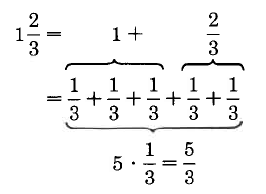
$Dos rectángulos, cada uno dividido en tres partes iguales con barras verticales. Cada parte contiene la fracción, un tercio. Debajo del rectángulo de la izquierda hay un corchete que agrupa las tres partes para formar una. Debajo del rectángulo de la derecha hay un corchete debajo de dos de las tres partes, haciendo dos tercios. Los dos segmentos entre corchetes se suman juntos.$ $uno y dos tercios equivale a uno más dos tercios. Uno puede ampliarse a tres tercios, haciendo que el número original sea equivalente a la suma de cinco un tercio, o cinco tercios.$

Recordemos que la multiplicación describe la adición repetida.

Observe que se$\dfrac{5}{3}$ puede obtener$1 \dfrac{2}{3}$ mediante el uso de la multiplicación de la siguiente manera.

Multiplicar:$3 \cdot 1 = 3$

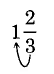
$uno y dos tercios, con una flecha dibujada del denominador al uno.$

Agregar:$3 + 2 = 5$. Coloca el 5 sobre el 3:$\dfrac{5}{3}$

En este ejemplo se ilustra el procedimiento para convertir un número mixto en una fracción impropia.

Convertir un número mixto en una fracción impropia
Para convertir un número mixto en una fracción impropia,

Multiplique el denominador de la parte fraccionaria del número mixto por la parte de número entero.
A este producto, agregue el numerador de la parte fraccionaria.
Coloca este resultado sobre el denominador de la parte fraccionaria.

Conjunto de Muestras B

Convierte cada número mixto en una fracción impropia.

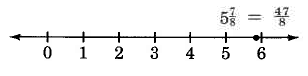
$5 \dfrac{7}{8}$

Solución

Multiplicar:$8 \cdot 5 = 40$
Agregar:$40 + 7 = 47$
Lugar 47 sobre 8:$\dfrac{47}{8}$

Así,$5 \dfrac{7}{8} = \dfrac{47}{8}$.

$Una línea numérica que muestra la ubicación de cinco y siete eigths, o 47 ochos.$

Conjunto de Muestras B

$16 \dfrac{2}{3}$

Solución

Multiplicar:$3 \cdot 16 = 48$.
Agregar:$48 + 2 = 50$
Lugar 50 sobre 3:$\dfrac{50}{3}$

Por lo tanto,$16 \dfrac{2}{3} = \dfrac{50}{3}$

Conjunto de práctica A

Convertir cada número mixto a su fracción impropia correspondiente.

$8 \dfrac{1}{4}$

Responder: $\dfrac{33}{4}$

Conjunto de práctica A

$5 \dfrac{3}{5}$

Responder: $\dfrac{28}{5}$

Conjunto de práctica A

$1 \dfrac{4}{15}$

Responder: $\dfrac{19}{15}$

Conjunto de práctica A

$12 \dfrac{2}{7}$

Responder: $\dfrac{86}{7}$

Ejercicios

Para los siguientes 15 problemas, identifique cada expresión como una fracción propia, una fracción impropia o un número mixto.

Ejercicio$\PageIndex{1}$

$\dfrac{3}{2}$

Responder: fracción impropia

Ejercicio$\PageIndex{2}$

$\dfrac{4}{9}$

Ejercicio$\PageIndex{3}$

$\dfrac{5}{7}$

Responder: fracción adecuada

Ejercicio$\PageIndex{4}$

$\dfrac{1}{8}$

Ejercicio$\PageIndex{5}$

$6 \dfrac{1}{4}$

Responder: número mixto

Ejercicio$\PageIndex{6}$

$\dfrac{11}{8}$

Ejercicio$\PageIndex{7}$

$\dfrac{1,001}{12}$

Responder: fracción impropia

Ejercicio$\PageIndex{8}$

$191 \dfrac{4}{5}$

Ejercicio$\PageIndex{9}$

$1 \dfrac{9}{13}$

Responder: número mixto

Ejercicio$\PageIndex{10}$

$31 \dfrac{6}{7}$

Ejercicio$\PageIndex{11}$

$3 \dfrac{1}{40}$

Responder: número mixto

Ejercicio$\PageIndex{12}$

$\dfrac{55}{12}$

Ejercicio$\PageIndex{13}$

$\dfrac{0}{9}$

Responder: fracción adecuada

Ejercicio$\PageIndex{14}$

$\dfrac{8}{9}$

Ejercicio$\PageIndex{15}$

$101 \dfrac{1}{11}$

Responder: número mixto

Para los siguientes 15 problemas, convierta cada una de las fracciones impropias a su número mixto correspondiente.

Ejercicio$\PageIndex{16}$

$\dfrac{11}{6}$

Ejercicio$\PageIndex{17}$

$\dfrac{14}{3}$

Responder: $4 \dfrac{2}{3}$

Ejercicio$\PageIndex{18}$

$\dfrac{25}{4}$

Ejercicio$\PageIndex{19}$

$\dfrac{35}{4}$

Responder: $8 \dfrac{3}{4}$

Ejercicio$\PageIndex{20}$

$\dfrac{71}{8}$

Ejercicio$\PageIndex{21}$

$\dfrac{63}{7}$

Responder: 9

Ejercicio$\PageIndex{22}$

$\dfrac{121}{11}$

Ejercicio$\PageIndex{23}$

$\dfrac{165}{12}$

Responder: $13 \dfrac{9}{12}$o$13 \dfrac{3}{4}$

Ejercicio$\PageIndex{24}$

$\dfrac{346}{15}$

Ejercicio$\PageIndex{25}$

$\dfrac{5,000}{9}$

Responder: $555 \dfrac{5}{9}$

Ejercicio$\PageIndex{26}$

$\dfrac{23}{5}$

Ejercicio$\PageIndex{27}$

$\dfrac{73}{2}$

Responder: $36 \dfrac{1}{2}$

Ejercicio$\PageIndex{28}$

$\dfrac{19}{2}$

Ejercicio$\PageIndex{29}$

$\dfrac{316}{41}$

Responder: $7 \dfrac{29}{41}$

Ejercicio$\PageIndex{30}$

$\dfrac{800}{3}$

Para los siguientes 15 problemas, convierta cada uno de los números mixtos a su fracción impropia correspondiente.

Ejercicio$\PageIndex{31}$

$4 \dfrac{1}{8}$

Responder: $\dfrac{33}{8}$

Ejercicio$\PageIndex{32}$

$1 \dfrac{5}{12}$

Ejercicio$\PageIndex{33}$

$6 \dfrac{7}{9}$

Responder: $\dfrac{61}{9}$

Ejercicio$\PageIndex{34}$

$15 \dfrac{1}{4}$

Ejercicio$\PageIndex{35}$

$10 \dfrac{5}{11}$

Responder: $\dfrac{115}{11}$

Ejercicio$\PageIndex{36}$

$15 \dfrac{3}{10}$

Ejercicio$\PageIndex{37}$

$8 \dfrac{2}{3}$

Responder: $\dfrac{26}{3}$

Ejercicio$\PageIndex{38}$

$4 \dfrac{3}{4}$

Ejercicio$\PageIndex{39}$

$21 \dfrac{2}{5}$

Responder: $\dfrac{107}{5}$

Ejercicio$\PageIndex{40}$

$17 \dfrac{9}{10}$

Ejercicio$\PageIndex{41}$

$9 \dfrac{20}{21}$

Responder: $\dfrac{209}{21}$

Ejercicio$\PageIndex{42}$

$5 \dfrac{1}{16}$

Ejercicio$\PageIndex{43}$

$90 \dfrac{1}{100}$

Responder: $\dfrac{9001}{100}$

Ejercicio$\PageIndex{44}$

$300 \dfrac{43}{1,000}$

Ejercicio$\PageIndex{45}$

$19 \dfrac{7}{8}$

Responder: $\dfrac{159}{8}$

Ejercicio$\PageIndex{46}$

¿Por qué$0 \dfrac{4}{7}$ no califica como número mixto?

Pista:

Consulte la definición de un número mixto.

Ejercicio$\PageIndex{47}$

¿Por qué 5 califica como número mixto?

Pista:

Consulte la definición de un número mixto.

Responder: ... porque puede ser wirtten como$5 \dfrac{0}{n}$, donde$n$ está cualquier número entero positivo.

Problemas de la calculadora
Para los siguientes 8 problemas, utilice una calculadora para convertir cada número mixto a su fracción impropia correspondiente.

Ejercicio$\PageIndex{48}$

$35 \dfrac{11}{12}$

Ejercicio$\PageIndex{49}$

$27 \dfrac{5}{61}$

Responder: $\dfrac{1,652}{61}$

Ejercicio$\PageIndex{50}$

$83 \dfrac{40}{41}$

Ejercicio$\PageIndex{51}$

$105 \dfrac{21}{23}$

Responder: $\dfrac{2,436}{23}$

Ejercicio$\PageIndex{52}$

$72 \dfrac{605}{606}$

Ejercicio$\PageIndex{53}$

$816 \dfrac{19}{25}$

Responder: $\dfrac{20,419}{25}$

Ejercicio$\PageIndex{54}$

$708 \dfrac{42}{51}$

Ejercicio$\PageIndex{55}$

$6,012 \dfrac{4,216}{8,117}$

Responder: $\dfrac{48,803,620}{8,117}$

Ejercicios para revisión

Ejercicio$\PageIndex{56}$

Redondear 2,614,000 al mil más cercano.

Ejercicio$\PageIndex{57}$

Encuentra el producto. $1,004 \cdot 1,005$

Responder: 1,009,020

Ejercicio$\PageIndex{58}$

Determina si 41,826 es divisible por 2 y 3.

Ejercicio$\PageIndex{59}$

Encuentra el mínimo común múltiplo de 28 y 36.

Responder: 252

Ejercicio$\PageIndex{60}$

Especificar el numerador y denominador de la fracción$\dfrac{12}{19}$.

Search

Text Color

Text Size

Margin Size

Font Type

Fracciones propias positivas

Fracciones impropias positivas

Números Mixtos Positivos

Relacionar fracciones impropias positivas y números mixtos positivos

Conversión de fracciones impropias a números mixtos

Conversión de números mixtos a fracciones impropias

Ejercicios

Ejercicios para revisión