18.6: Combinar polinomios usando multiplicación
- Última actualización
- 28 mar 2023
- Guardar como PDF
- Page ID
- 161261
( \newcommand{\kernel}{\mathrm{null}\,}\)
Multiplicar un polinomio por un monomio
Multiplicar un polinomio por un monomio es una aplicación directa de la propiedad distributiva.
Propiedad distributiva
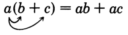
La propiedad distributiva sugiere la siguiente regla.
Multiplicar un polinomio por un monomio
Para multiplicar un polinomio por un monomio, multiplique cada término del polinomio por el monomio y luego sumar los productos resultantes juntos.
Conjunto de Muestras A
Ejemplo18.6.1
\ (\ comenzar {alineado}
3 (x+9) &=3\ cdot x+3\ cdot 9\\
&=3 x+27
\ final {alineado}\)
Ejemplo18.6.2
\ (\ comenzar {alineado}
6\ izquierda (x^ {3} -2 x\ derecha) =6\ izquierda (x^ {3} + (-2 x)\ derecha) &=6\ cdot x^ {3} +6 (-2 x)\\
&=6 x^ {3} -12 x
\ end {alineado}\)
Ejemplo18.6.3
\ (\ comenzar {alineado}
(x-7) x &=x\ cdot x+x (-7)\\
&=x^ {2} -7 x
\ final {alineado}\)
Ejemplo18.6.4
\ (\ begin {alineado}
8 a^ {2}\ izquierda (3 a^ {4} -5 a^ {3} +a\ derecha) &=8 a^ {2}\ cdot 3 a^ {4} +8 a^ {2}\ izquierda (-5 a^ {3}\ derecha) +8 a^ {2}\ cdot a\\
&=24 a^ {6} -40 a^ {5} +8 a^ {3}
\ final {alineado}\)
Ejemplo18.6.5
\ (\ begin {alineado}
4 x^ {2} y^ {7} z\ izquierda (x^ {6} y+8 y^ {2} z^ {2} z^ {2}\ derecha) &=4 x^ {2} y^ {7} z\ cdot x^ {5} y+4 x^ {2} y^ {7} z\ cdot 8 y^ {2} z^ {2}
&=4 x^ {7} y^ {8} z+32 x^ {2} y^ {9} z^ {3}
\ final {alineado}\)
Ejemplo18.6.6
10ab2c(125a2)=1250a3b2c
Ejemplo18.6.7
\ (\ comenzar {alineado}
\ izquierda (9 x^ {2} z+4 w\ derecha)\ izquierda (5 z w^ {3}\ derecha) &=9 x^ {2} z\ cdot 5 z w^ {3} +4 w\ cdot 5 z w^ {3}\\
&=45 x^ {2} z^ {2} z^ {2} w^ {3} +20 z w^ {4}\\
&=45 x^ {2} w^ {3} z^ {2} +20 w^ {4} z
\ end {alineado}\)
Conjunto de práctica A
Determinar los siguientes productos.
Problema de práctica18.6.1
3(x+8)
- Contestar
-
3x+24
Problema de práctica18.6.2
(2+a)4
- Contestar
-
4a+8
Problema de práctica18.6.3
(a2−2b+6)2a
- Contestar
-
2a3−4ab+12a
Problema de práctica18.6.4
8a2b3(2a+7b+3)
- Contestar
-
16a3b3+56a2b4+24a2b3
Problema de práctica18.6.5
4x(2x5+6x4−8x3−x2+9x−11)
- Contestar
-
8x6+24x5−32x4−4x3+36x2−44x
Problema de práctica18.6.6
(3a2b)(2ab2+4b3)
- Contestar
-
6a3b3+12a2b4
Problema de práctica18.6.7
5mn(m2n2+m+n0),n≠0
- Contestar
-
5m3n3+5m2n+5mn
Problema de práctica18.6.8
6.03(2.11a3+8.00a2b)
- Contestar
-
12.7233a3+48.24a2b
Simplificando+(a+b) y−(a+b)
+(a+b)y−(a+b)
A menudo, encontraremos multiplicaciones de la forma
+1(a+b) o−1(a+b)
Estos términos aparecerán realmente como
+(a+b) y−(a+b)
Usando la propiedad distributiva, nosotros puede eliminar los paréntesis.
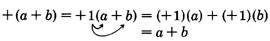
Se han eliminado los paréntesis y el signo de cada término se ha mantenido igual.
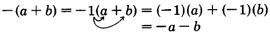
Se han eliminado los paréntesis y se ha cambiado el signo de cada término a su opuesto.
- Para eliminar un conjunto de paréntesis precedidos de un signo “+”, basta con quitar los paréntesis y dejar el signo de cada término igual.
- Para eliminar un conjunto de paréntesis precedidos de un signo “−”, elimine los paréntesis y cambie el signo de cada término a su signo opuesto.
Conjunto de Muestras B
Simplifica las expresiones.
Ejemplo18.6.8
(6x−1).
Este conjunto de paréntesis va precedido de un signo “+” (implícito). Simplemente dejamos caer los paréntesis.
(6x−1)=6x−1
Ejemplo18.6.9
(14a2−6a3b2+ab4)=14a2b3−6a3b2+ab4
Ejemplo18.6.10
−(21a2+7a−18)
Este conjunto de paréntesis va precedido de un signo “−”. Podemos dejar los paréntesis siempre y cuando cambiemos el signo de cada término dentro de los paréntesis a su signo opuesto.
−(21a2+7a−18)=−21a2−7a+18
Ejemplo18.6.11
−(7y3−2y2+9y+1)=−7y3+2y2−9y−1
Set de práctica B
Simplifique quitando los paréntesis.
Problema de práctica18.6.9
(2a+3b)
- Contestar
-
2a+3b
Problema de práctica18.6.10
(a2−6a+10)
- Contestar
-
a2−6a+10
Problema de práctica18.6.11
−(x+2y)
- Contestar
-
−x−2y
Problema de práctica18.6.12
−(5m−2n)
- Contestar
-
−5m+2n
Problema de práctica18.6.13
−(−3s2−7s+9)
- Contestar
-
3s2+7s−9
Multiplicar un polinomio por un polinomio
Como podemos considerar una expresión encerrada entre paréntesis como una sola cantidad, tenemos, por la propiedad distributiva,
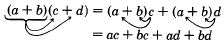
Para mayor comodidad, utilizaremos la propiedad conmutativa de suma para escribir esta expresión de manera que los dos primeros términos contengan a y los dos segundos contengan b.
(a+b)(c+d)=ac+ad+bc+bd
Este método se llama comúnmente el método FOIL.
- F: Primeros Términos
- O: Términos externos
- I: Términos internos
- L: Ultimos Términos
(a+b)(2+3)=(a+b)+(a+b)⏟2 terms +(a+b)+(a+b)+(a+b)⏟3 terms
Reorganizar,
\ (\ begin {array} {l}
=a+a+b+a+a+a+b+b+b\
= 2 a+2 b+3 a+3 b
\ end {array}\)
Combinando términos similares,
\ (\ begin {array} {l}
=5a + 5b
\ end {array}\)
Este uso de la propiedad distributiva sugiere la siguiente regla.
Multiplicación de un polinomio por un polinomio
Para multiplicar dos polinomios juntos, multiplique cada término de un polinomio por cada término del otro polinomio.
Conjunto de Muestras C
Realiza las siguientes multiplicaciones y simplifica.
Ejemplo18.6.12
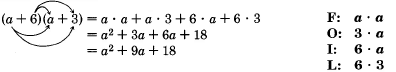
Con algo de práctica, el segundo y tercer término se pueden combinar mentalmente.
Ejemplo18.6.13
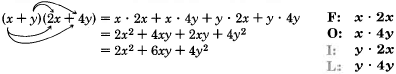
Ejemplo18.6.14
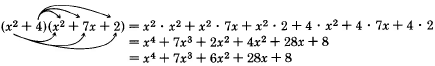
Ejemplo18.6.15
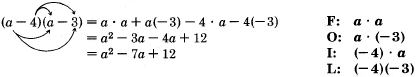
Ejemplo18.6.16
\ (\ begin {alineado}
(m-3) ^ {2} &= (m-3) (m-3)\\
&=m\ cdot m+m (-3) -3\ cdot m-3 (-3)\\
&=m^ {2} -3 m-3 m+9\\
&=m^ {2} -6 m+9
\ final {alineado}\)
Ejemplo18.6.17
\ (\ begin {alineado}
(x+5) ^ {3} & =( x+5) (x+5) (x+5) (x+5) &\ text {Asociar los dos primeros factores.}\\
&= [(x+5) (x+5)] (x+5)\
&=\ left [x^ {2} +5 x+5 x+25\ right] (x+5)\
&=\ left [x^ {2} +10 x+25\ derecha] (x+5)\\
&=x^ {2}\ cdot x+x^ {2} \ cdot 5+10 x\ cdot x+10 x\ cdot 5+25\ cdot x+25\ cdot 5\\
&=x^ {3} +5 x^ {2} +10 x^ {2} +50 x+25 x+125\\
&=x^ {3} +15 x^ {2} +75 x+125
\ final {alineado}\)
Set de práctica C
Encuentra los siguientes productos y simplifica.
Problema de práctica18.6.14
(a+1)(a+4)
- Contestar
-
a2+5a+4
Problema de práctica18.6.15
(m−9)(m−2)
- Contestar
-
m2−11m+18
Problema de práctica18.6.16
(2x+4)(x+5)
- Contestar
-
2x2+14x+20
Problema de práctica18.6.17
(x+y)(2x−3y)
- Contestar
-
2x2−xy−3y2
Problema de práctica18.6.18
(3a2−1)(5a2+a)
- Contestar
-
15a4+3a3−5a2−a
Problema de práctica18.6.19
(2x2y3+xy2)(5x3y2+x2y)
- Contestar
-
10x5y5+7x4y4+x3y3
Problema de práctica18.6.20
(a+3)(a2+3a+6)
- Contestar
-
a3+6a2+15a+18
Problema de práctica18.6.21
(a+4)(a+4)
- Contestar
-
a2+8a+16
Problema de práctica18.6.22
(r−7)(r−7)
- Contestar
-
r2−14r+49
Problema de práctica18.6.23
(x+6)2
- Contestar
-
x2+12x+36
Problema de práctica18.6.24
(y−8)2
- Contestar
-
y2−16y+64
Conjunto de Muestras D
Realizar las siguientes adiciones y restas.
Ejemplo18.6.18
3x+7+(x−3). Primero debemos quitar los paréntesis. Están precedidos de un signo+ ""”, así que los quitamos y dejamos el signo de cada término igual.
3x+7+x−3Combina términos similares.
4x+4
Ejemplo18.6.19
5y3+11−(12y3−2). Primero eliminamos los paréntesis. Están precedidos por un signo "−"”, así que los quitamos y cambiamos el signo de cada término dentro de ellos.
5y3+11−12y3+2Combina términos similares.
−7y3+13
Ejemplo18.6.20
Agregar4x2+2x−8 a3x2−7x−10
\ (\ begin {array} {l}
\ izquierda (4 x^ {2} +2 x-8\ derecha) +\ izquierda (3 x^ {2} -7 x-10\ derecha)\\
4 x^ {2} +2 x-8+3 x^ {2} -7 x-10\\
7 x^ {2} -5 x-18
\ end {array}\)
Ejemplo18.6.21
Restar8x2−5x+2 de3x2+x−12.
\ (\ begin {array} {l}
\ izquierda (3 x^ {2} +x-12\ derecha) -\ izquierda (8 x^ {2} -5 x+2\ derecha)\\
3 x^ {2} +x-12-8 x^ {2} +5 x-2\
-5 x^ {2} +6 x-14
\ end {array}\)
Ten mucho cuidado de no escribir este problema como:
3x2+x−12−8x2−5x+2
Esta forma nos hace restar sólo el primer término,8x2, en lugar de toda la expresión. Use paréntesis.
Otra forma incorrecta es:
8x2−5x+2−(3x2+x−12)
Esta forma nos hace realizar la resta en el orden equivocado.
Set de Práctica D
Realizar las siguientes adiciones y restas.
Problema de práctica18.6.25
6y2+2y−1+(5y2−18)
- Contestar
-
11y2+2y−19
Problema de práctica18.6.26
(9m−n)−(10m+12n)
- Contestar
-
−m−13n
Problema de práctica18.6.27
Agregar2r2+4r−1 a3r2−r−7
- Contestar
-
5r2+3r−8
Problema de práctica18.6.28
Restar4s−3 de7s+8.
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Ejercicios
Para los siguientes problemas, realice la multiplicación y combine cualquier término similar.
Ejercicio18.6.1
7(x+6)
- Contestar
-
7x+42
Ejercicio18.6.2
4(y+3)
Ejercicio18.6.3
6(y+4)
- Contestar
-
6y+24
Ejercicio18.6.4
8(m+7)
Ejercicio18.6.5
5(a−6)
- Contestar
-
5a−30
Ejercicio18.6.6
2(x−10)
Ejercicio18.6.7
3(4x+2)
- Contestar
-
12x+6
Ejercicio18.6.8
6(3x+4)
Ejercicio18.6.9
9(4y−3)
- Contestar
-
36y−27
Ejercicio18.6.10
5(8m−6)
Ejercicio18.6.11
−9(a+7)
- Contestar
-
−9a−63
Ejercicio18.6.12
−3(b+8)
Ejercicio18.6.13
−4(x+2)
- Contestar
-
−4x−8
Ejercicio18.6.14
−6(y+7)
Ejercicio18.6.15
−3(a−6)
- Contestar
-
−3a+18
Ejercicio18.6.16
−9(k−7)
Ejercicio18.6.17
−5(2a+1)
- Contestar
-
−10a−5
Ejercicio18.6.18
−7(4x+2)
Ejercicio18.6.19
−3(10y−6)
- Contestar
-
−30y+18
Ejercicio18.6.20
−8(4y−11)
Ejercicio18.6.21
x(x+6)
- Contestar
-
x2+6x
Ejercicio18.6.22
y(y+7)
Ejercicio18.6.23
m(m−4)
- Contestar
-
m2−4m
Ejercicio18.6.24
k(k−11)
Ejercicio18.6.25
3x(x+2)
- Contestar
-
3x2+6x
Ejercicio18.6.26
4y(y+7)
Ejercicio18.6.27
6a(a−5)
- Contestar
-
6a2−30a
Ejercicio18.6.28
9x(x−3)
Ejercicio18.6.29
3x(5x+4)
- Contestar
-
15x2+12x
Ejercicio18.6.30
4m(2m+7)
Ejercicio18.6.31
2b(b−1)
- Contestar
-
2b2−2b
Ejercicio18.6.32
7a(a−4)
Ejercicio18.6.33
3x2(5x2+4)
- Contestar
-
15x4+12x2
Ejercicio18.6.34
9y3(3y2+2)
Ejercicio18.6.35
4a4(5a3+3a2+2a)
- Contestar
-
20a7+12a6+8a5
Ejercicio18.6.36
2x4(6x3−5x2−2x+3)
Ejercicio18.6.37
−5x2(x+2)
- Contestar
-
−5x3−10x2
Ejercicio18.6.38
−6y3(y+5)
Ejercicio18.6.39
2x2y(3x2y2−6x)
- Contestar
-
6x4y3−12x3y
Ejercicio18.6.40
8a3b2c(2ab3+3b)
Ejercicio18.6.41
b5x2(2bx−11)
- Contestar
-
2b6x3−11b5x2
Ejercicio18.6.42
4x(3x2−6x+10)
Ejercicio18.6.43
9y3(2y4−3y3+8y2+y−6)
- Contestar
-
18y7−27y6+72y5+9y4−54y3
Ejercicio18.6.44
−a2b3(6ab4+5ab3−8b2+7b−2)
Ejercicio18.6.45
(a+4)(a+2)
- Contestar
-
a2+6a+8
Ejercicio18.6.46
(x+1)(x+7)
Ejercicio18.6.47
(y+6)(y−3)
- Contestar
-
y2+3y−18
Ejercicio18.6.48
(t+8)(t−2)
Ejercicio18.6.49
(i−3)(i+5)
- Contestar
-
i2+2i−15
Ejercicio18.6.50
(x−y)(2x+y)
Ejercicio18.6.51
(3a−1)(2a−6)
- Contestar
-
6a2−20a+6
Ejercicio18.6.52
(5a−2)(6a−8)
Ejercicio18.6.53
(6y+11)(3y+10)
- Contestar
-
18y2+93y+110
Ejercicio18.6.54
(2t+6)(3t+4)
Ejercicio18.6.55
(4+x)(3−x)
- Contestar
-
−x2−x+12
Ejercicio18.6.56
(6+a)(4+a)
Ejercicio18.6.57
(x2+2)(x+1)
- Contestar
-
x3+x2+2x+2
Ejercicio18.6.58
(x2+5)(x+4)
Ejercicio18.6.59
(3x2−5)(2x2+1)
- Contestar
-
6x4−7x2−5
Ejercicio18.6.60
(4a2b3−2a)(5a2b−3b)
Ejercicio18.6.61
(6x3y4+6x)(2x2y3+5y)
- Contestar
-
12x5y7+30x3y5+12x3y3+30xy
Ejercicio18.6.62
5(x−7)(x−3)
Ejercicio18.6.63
4(a+1)(a−8)
- Contestar
-
4a2−28a−32
Ejercicio18.6.64
a(a−3)(a+5)
Ejercicio18.6.65
x(x+1)(x+4)
- Contestar
-
x3+5x2+4x
Ejercicio18.6.66
y3(y−3)(y−2)
- Contestar
-
y5−5y4+6y3
Ejercicio18.6.67
2a2(a+4)(a+3)
Ejercicio18.6.68
5y6(y+7)(y+1)
- Contestar
-
5y8+40y7+35y6
Ejercicio18.6.69
ab2(a2−2b)(a+b4)
Ejercicio18.6.70
x3y2(5x2y2−3)(2xy−1)
- Contestar
-
10x6y5−5x5y4−6x4y3+3x3y2
Ejercicio18.6.71
6(a2+5a+3)
Ejercicio18.6.72
8(c3+5c+11)
- Contestar
-
8c3+40c+88
Ejercicio18.6.73
3a2(2a3−10a2−4a+9)
Ejercicio18.6.74
6a3b3(4a2b6+7ab8+2b10+14)
- Contestar
-
24a5b9+42a4b11+12a3b13+18a3b3
Ejercicio18.6.75
(a−4)(a2+a−5)
Ejercicio18.6.76
(x−7)(x2+x−3)
- Contestar
-
x3−6x2−10x+21
Ejercicio18.6.77
(2x+1)(5x3+6x2+8)
Ejercicio18.6.78
(7a2+2)(3a5−4a3−a−1)
- Contestar
-
21a7−22a5−15a3−7a2−2a−2
Ejercicio18.6.79
(x+y)(2x2+3xy+5y2)
Ejercicio18.6.80
(2a+b)(5a2+4a2b−b−4)
- Contestar
-
10a3+8a3b+4a2b2+5a2b−b2−8a−4b−2ab
Ejercicio18.6.81
(x+3)2
Ejercicio18.6.82
(x+1)2
- Contestar
-
x2+2x+1
Ejercicio18.6.83
(x−5)2
Ejercicio18.6.84
(a+2)2
- Contestar
-
a2+4a+4
Ejercicio18.6.85
(a−9)2
Ejercicio18.6.86
−(3x−5)2
- Contestar
-
−9x2+30x−25
Ejercicio18.6.87
−(8t+7)2
Para los siguientes problemas, realice las operaciones indicadas y combine términos similares.
Ejercicio18.6.88
3x2+5x−2+(4x2−10x−5)
- Contestar
-
7x2−5x−7
Ejercicio18.6.89
−2x3+4x2+5x−8+(x3−3x2−11x+1)
Ejercicio18.6.90
−5x−12xy+4y2+(−7x+7xy−2y2)
- Contestar
-
2y2−5xy−12x
Ejercicio18.6.91
(6a2−3a+7)−4a2+2a−8
Ejercicio18.6.92
(5x2−24x−15)+x2−9x+14
- Contestar
-
6x2−33x−1
Ejercicio18.6.93
(3x3−7x2+2)+(x3+6)
Ejercicio18.6.94
(9a2b−3ab+12ab2)+ab2+2ab
- Contestar
-
9a2b+13ab2−ab
Ejercicio18.6.95
6x2−12x+(4x2−3x−1)+4x2−10x−4
Ejercicio18.6.96
5a3−2a−26+(4a3−11a2+2a)−7a+8a3+20
- Contestar
-
17a3−11a2−7a−6
Ejercicio18.6.97
2xy−15−(5xy+4)
Ejercicio18.6.98
Agregar4x+6 a8x−15.
- Contestar
-
12x−9
Ejercicio18.6.99
Agregar5y2−5y+1 a−9y2+4y−2
Ejercicio18.6.100
Agregar3(x+6) a4(x−7)
- Contestar
-
7x−10
Ejercicio18.6.101
Agregar−2(x2−4) a5(x2+3x−1)
Ejercicio18.6.102
Agregar cuatro veces5x+2 a tres veces2x−1
- Contestar
-
26x+5
Ejercicio18.6.103
Agregar cinco veces−3x+2 a siete veces4x+3
Ejercicio18.6.104
Agregar−4 tiempos9x+6 a−2 tiempos−8x−3.
- Contestar
-
−20x−18
Ejercicio18.6.105
Restar6x2−10x+4 de3x2−2x+5
Ejercicio18.6.106
Restara2−16 dea2−16
- Contestar
-
0
Ejercicios para la revisión
Ejercicio18.6.107
Simplificar(15x2y45xy2)4
Ejercicio18.6.108
Exprese el número198,000 usando notación científica.
- Contestar
-
1.98×105
Ejercicio18.6.109
¿Cuántos4a2x3 hay adentro−16a4x5?
Ejercicio18.6.110
Indicar el grado del polinomio4xy3+3x5y−5x3y3, y escribir el coeficiente numérico de cada término.
- Contestar
-
El grado es 6; 4, 3, -5
Ejercicio18.6.111
Simplificar3(4x−5)+2(5x−2)−(x−3).


